что такое сечение куба

Как построить куб в перспективе: пошаговый метод

Здравствуйте, подписчики моего блога!

Многие сталкивались со сложностью в рисовании, когда хотели изобразить сложный по форме объект. Дело в том, что в основе всех сложных структур скрываются простые формы. И куб – одна из таких форм. Сегодня мы подробно разберем, как построить куб.

Перспектива

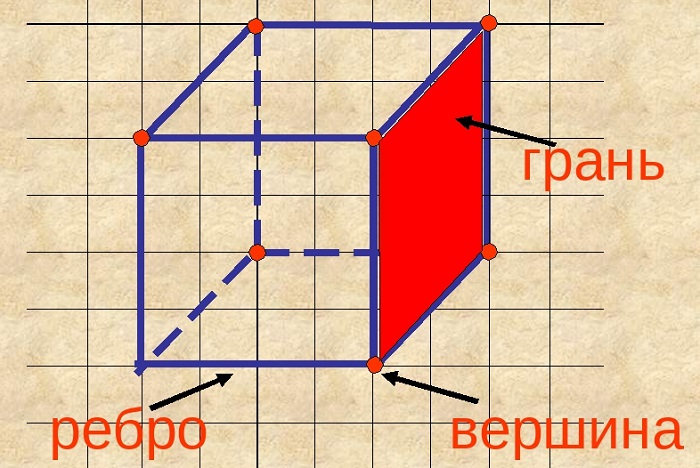
Куб – это геометрическое тело, состоящее из 6 плоскостей. Знаете, чем отличается куб от квадрата? Куб – это объемная фигура. А при рисовании любых объемных фигур нужно помнить о перспективе.

Из-за законов перспективы стороны куба будут сокращаться, иными словами становиться меньше.

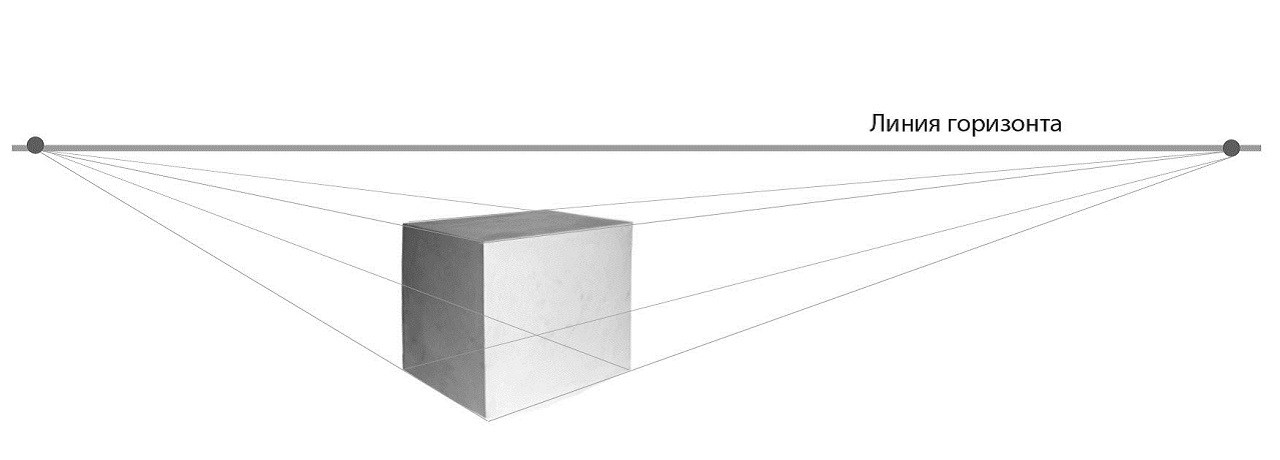
Для начала нужно определить линию горизонта. Это необходимо для того, чтобы правильно построить куб в перспективе.

Линия горизонта – это уровень глаз художника. На ней будут располагаться две точки схода. В каждую из этих точек придёт по 4 линии. Наглядно такой рисунок будет выглядеть следующим образом:

Рисуем пошагово

Чтобы было проще воспринять последовательность действий, давайте нарисуем куб пошагово.

Прежде чем заниматься перспективой куба, нужно наметить верные размеры предмета и определить его положение в листе. Куб не должен быть слишком маленьким или, наоборот, слишком большим.

Шаг 1 — Композиция

Композиция – это начало любой работы. От точного нахождения композиции зависит 50% успеха работы.

Следует оставить чуть больше расстояния сверху, чем снизу. Это придаст ощущение весомости.

Начинаем рисунок с самого ближнего к нам ребра куба. Наметьте его так, чтобы оно не совпадало с центром листа. Легкими засечками определяем высоту этого ребра. Так как оно находится ближе всего, его высота будет больше остальных ребер.

Шаг 2 — Сокращение

Плоскости в кубе заметно удаляются в силу перспективного сокращения. Чтобы верно определить это сокращение на листе, необходимо определить углы наклона ребер.

Проводим горизонтальную линию, параллельную листу бумаги, она поможет определить какой угол меньше, а какой больше. Тренируйте свой глаз, переводите взгляд с куба на рисунок, таким образом, перепроверяя себя.

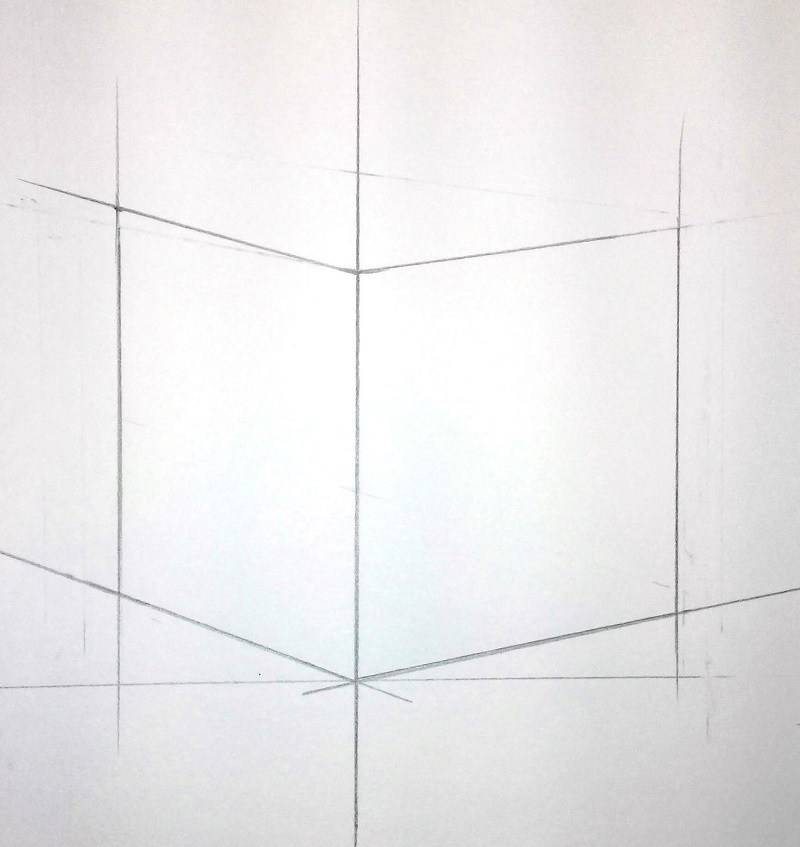
Шаг — 3 — Линейная перспектива

Чтобы куб «лег» в пространство, ребра, удаленные от нас, мы рисуем выше и меньше. Этот прием лежит в основе линейной перспективы. Найдите, где заканчиваются эти ребра и обозначьте их точками. Сечение куба по трем точкам – это верных способ при построении.

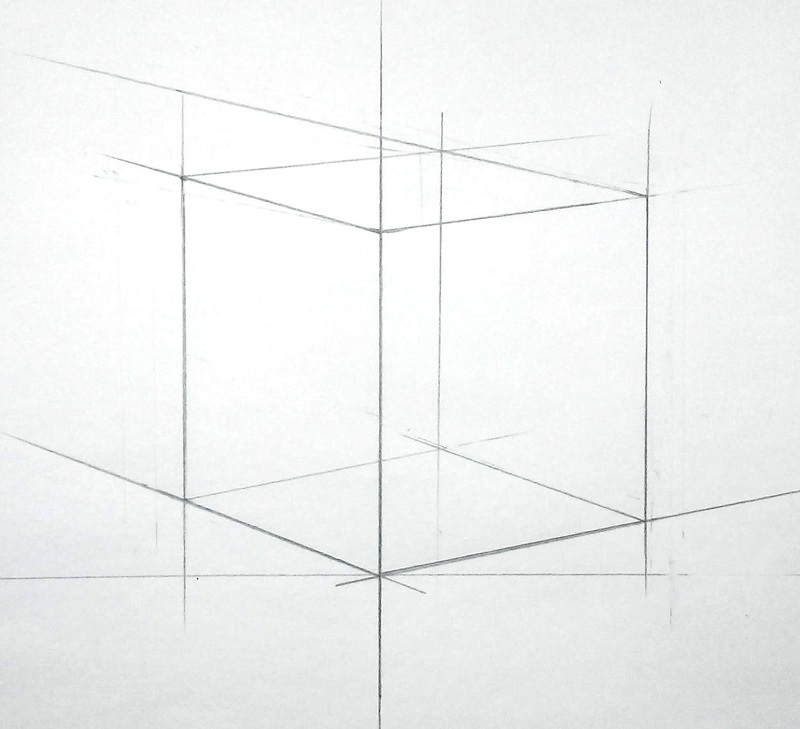
Соединяем горизонтальными линиями пересечения плоскостей в кубе. Помните о том, что они сокращаются, и, если, мы их продлим, то они сойдутся в точке схода.

Невидимые грани мы также должны нарисовать. При правильном построении нужно проверить все сокращения, чтобы не было обратной перспективы.

Шаг 4 — Проверка пропорций

Также можно использовать метод визирования. Вы наверняка замечали, как художники вытягивают руку и измеряют пропорции? Это и есть метод визирования.

Для того, чтобы проверить пропорции, закройте один глаз, возьмите карандаш и на вытянутой руке сопоставьте его кончик с верхом переднего ребра куба. Большой палец передвиньте в то место, где ребро заканчивается.

Высота ребра найдена. Теперь, не переставляя палец, наклоните кисть руки на 90 градусов и уже по горизонтали сопоставьте величину одного ребра с другим. Таким образом вы можете проверять и другие величины.

С опытом художники измеряют пропорции «на глаз», это значит, что они обходятся без метода визирования. Их глаз настолько натренирован, что видит размеры без измерений.

Итак, линейное построение подошло к концу, а значит, мы переходим к воздушной перспективе или, проще говоря, к штрихованию.

Штрихование

Основная задача рисунка – это передать объем. Внимательно посмотрите на предмет, определите для себя тональность каждой из сторон.

Штриховать следует по форме куба. Внимательно подходите к штриховке, не стоит излишне чернить, все-таки мы рисуем гипсовый куб.

Набирайте тон постепенно, не старайтесь все сделать за один подход. Штрихи можно накладывать и в диагональном направлении.

Используйте карандаши разной мягкости. Для освещённой стороны отлично подойдет твердый карандаш – H, для полутона – HB, а для теневой стороны – B.

В некоторых случаях карандаши стоит выбирать индивидуально: некоторые люди имеют «легкую» руки и штрихуют еле заметно, а есть те, кто с помощью HB может довести рисунок до черноты.

Падающая тень

Как построить тень от куба? Чтобы падающая тень была убедительной, давайте рассмотрим основные принципы построения тени на поверхности листа.

Падающая тень всегда темнее, чем собственная тень на предмете. Чем ближе она подходит к объекту, тем темнее она становится.

На самом кубе тон становится также активнее на границе двух плоскостей – освещенной и теневой. Теневая сторона, по мере удаления в пространство, высветляется за счет отраженного света от поверхности. Рефлексы помогают передать световоздушное пространство.

Заключение

Мы поговорили о сечении куба плоскостью, о том, как правильно построить куб с натуры в перспективе. Рисование простых геометрических тел весьма полезно для начинающих и тех, кто хочет овладеть академическим рисунком.

Геометрия и расположение плоскостей в пространстве очень хорошо тренирует зрительное восприятие.

Если у вас нет гипсового куба, не беда, смастерите куб из бумаги. Для первых упражнений главное – это понять основные принципы при построении. А затем, можно будет перейти к гипсовым фигурам.

Удачи в творчестве! Рисуйте то, что любите!

Если вам понравилась статья, поделитесь ей с друзьями!

Источник

Узнать ещё

Знание — сила. Познавательная информация

Сечение куба плоскостью

Задачи на построение сечений куба плоскостью, как правило, проще чем, например, задачи на сечения пирамиды.

Провести прямую можем через две точки, если они лежат в одной плоскости. При построении сечений куба возможен еще один вариант построения следа секущей плоскости. Поскольку две параллельные плоскости третья плоскость пересекает по параллельным прямым, то, если в одной из граней уже построена прямая, а в другой есть точка, через которую проходит сечение, то можем провести через эту точку прямую, параллельную данной.

Рассмотрим на конкретных примерах, как построить сечения куба плоскостью.

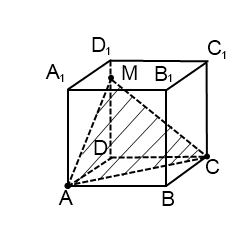
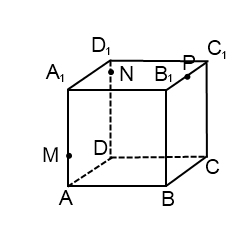
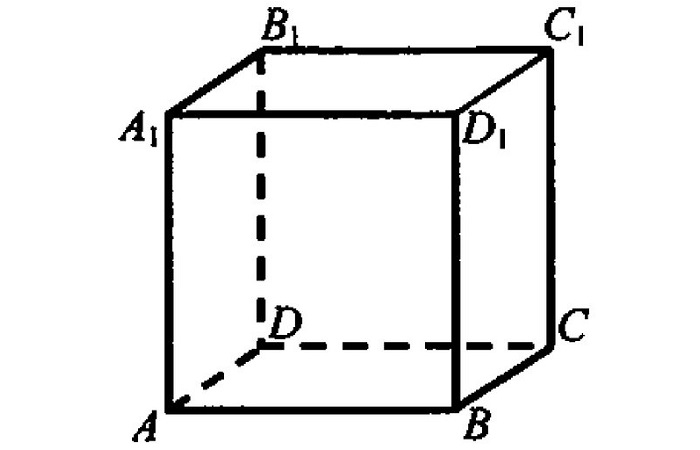
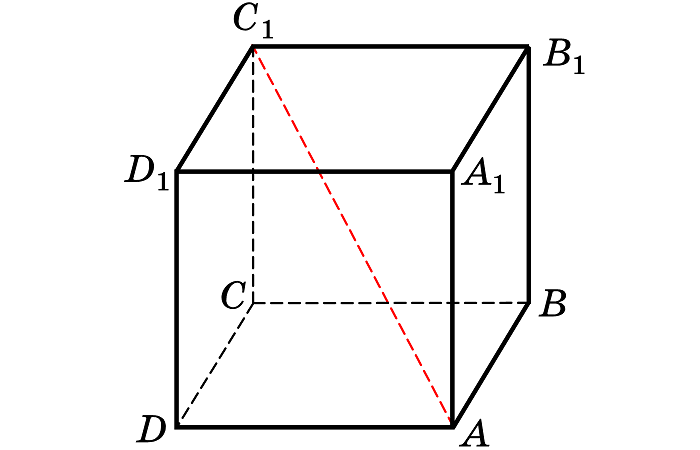
1) Построить сечение куба плоскостью, проходящей через точки A, C и M.

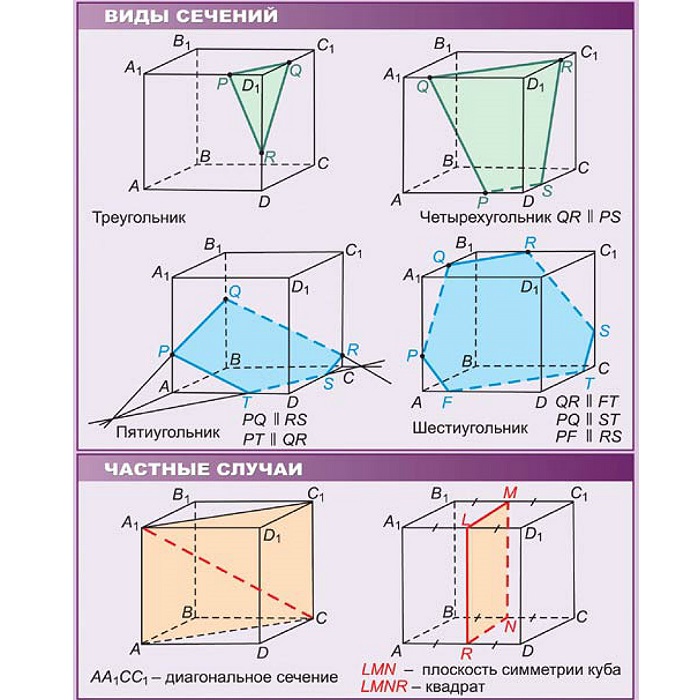
Задачи такого вида — самые простые из всех задач на построение сечений куба. Поскольку точки A и C лежат в одной плоскости (ABC), то через них можем провести прямую. Ее след — отрезок AC. Он невидим, поэтому изображаем AC штрихом. Аналогично соединяем точки M и C, лежащие в одной плоскости (CDD1), и точки A и M, которые лежат в одной плоскости (ADD1). Треугольник ACM — искомое сечение.

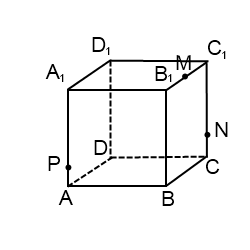
2) Построить сечение куба плоскостью, проходящей через точки M, N, P.

Здесь только точки M и N лежат в одной плоскости (ADD1), поэтому проводим через них прямую и получаем след MN (невидимый). Поскольку противолежащие грани куба лежат в параллельных плоскостях, то секущая плоскость пересекает параллельные плоскости (ADD1) и (BCC1) по параллельным прямым. Одну из параллельных прямых мы уже построили — это MN.

Через точку P проводим прямую, параллельную MN. Она пересекает ребро BB1 в точке S. PS — след секущей плоскости в грани (BCC1).

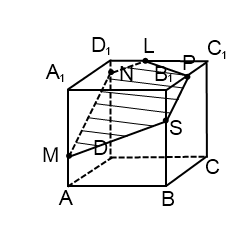
Проводим прямую через точки M и S, лежащие в одной плоскости (ABB1). Получили след MS (видимый).

Плоскости (ABB1) и (CDD1) параллельны. В плоскости (ABB1) уже есть прямая MS, поэтому через точку N в плоскости (CDD1) проводим прямую, параллельную MS. Эта прямая пересекает ребро D1C1 в точке L. Ее след — NL (невидимый). Точки P и L лежат в одной плоскости (A1B1C1), поэтому проводим через них прямую.

Пятиугольник MNLPS — искомое сечение.

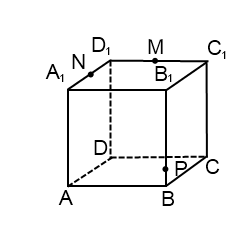
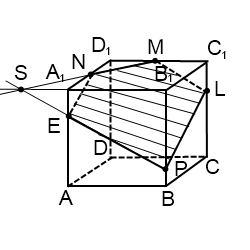
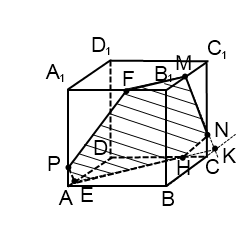
3) Построить сечение куба плоскостью, проходящей через точки M, N, P.

Точки M и N лежат в одной плоскости (ВСС1), поэтому через них можно провести прямую. Получаем след MN (видимый). Плоскость (BCC1) параллельна плоскости (ADD1),поэтому через точку P, лежащую в (ADD1), проводим прямую, параллельную MN. Она пересекает ребро AD в точке E. Получили след PE (невидимый).

Больше нет точек, лежащей в одной плоскости, или прямой и точки в параллельных плоскостях. Поэтому надо продолжить одну из уже имеющихся прямых, чтобы получить дополнительную точку.

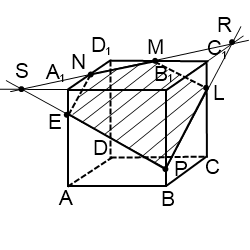
Плоскости (ABC) и (A1B1C1) параллельны. В одной из них есть прямая EH, в другой — точка M. Можем провести через M прямую, параллельную EH. Получаем след MF (видимый). Проводим прямую через точки M и F.

Шестиугольник MNHEPF — искомое сечение.

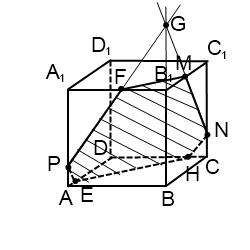
Если бы мы продолжили прямую MN до пересечения с другой прямой плоскости (BCC1), с BB1, то получили бы точку G, принадлежащую плоскости (ABB1). А значит, через G и P можно провести прямую, след которой PF. Далее — проводим прямые через точки, лежащие в параллельных плоскостях, и приходим к тому же результату.

Работа с прямой PE дает то же сечение MNHEPF.

4) Построить сечение куба плоскостью, проходящей через точку M, N, P.

Здесь можем провести прямую через точки M и N, лежащие в одной плоскости (A1B1C1). Ее след — MN (видимый). Больше нет точек, лежащих в одной плоскости либо в параллельных плоскостях.

Продолжим прямую MN. Она лежит в плоскости (A1B1C1), поэтому пересечься может только с одной из прямых этой плоскости. С A1D1 и C1D1 точки пересечения уже есть — N и M. Еще две прямые этой плоскости — A1B1 и B1C1. Точка пересечения A1B1 и MN — S. Поскольку она лежит на прямой A1B1, то принадлежит плоскости ( ABB1), а значит, через нее и точку P, лежащую в этой же плоскости, можно провести прямую. Прямая PS пересекает ребро AA1 в точке E. PE — ее след (видимый). Через точки N и E, лежащие в одной плоскости (ADD1), можно провести прямую, след которой — NE (невидимый). В плоскости (ADD1) есть прямая NE, в параллельной ей плоскости (BCC1) — точка P. Через точку P можем провести прямую PL, параллельную NE. Она пересекает ребро CC1 в точке L. PL — след этой прямой (видимый). Точки M и L лежат в одной плоскости (CDD1), значит, через них можно провести прямую. Ее след — ML (невидимый). Пятиугольник MLPEN — искомое сечение.

Можно было продолжать прямую NM в обе стороны и искать ее точки пересечения не только с прямой A1B1, но и с прямой B1C1, также лежащей в плоскости (A1B1C1). В этом случае через точку P проводим сразу две прямые: одну — в плоскости (ABB1) через точки P и S, а вторую — в плоскости (BCC1), через точки P и R. После чего остается соединить лежащие в одной плоскости точки: M c L, E — с N.

Источник

Геометрические фигуры. Куб.

Куб или правильный гексаэдр – это правильный многогранник, у которого все грани это квадраты.

Куб является частным случаем параллелепипеда и призмы. 4 сечения куба имеют вид правильных

шестиугольников — это сечения через центр куба перпендикулярно 4-м главным диагоналям.

В кубе насчитывается шесть квадратов. Все вершины куба являются вершинами 3-х квадратов. То есть,

сумма плоских углов у каждой вершины = 270º.

Число сторон у грани – 4;

Общее число граней – 6;

Число рёбер примыкающих к вершине – 3;

Общее число вершин – 8;

Общее число рёбер – 12;

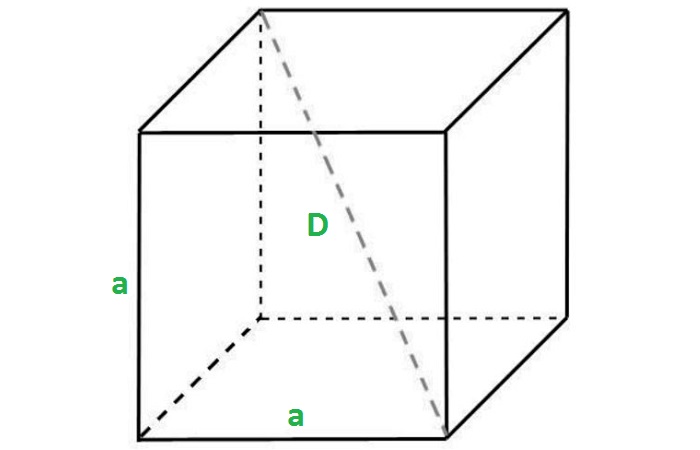
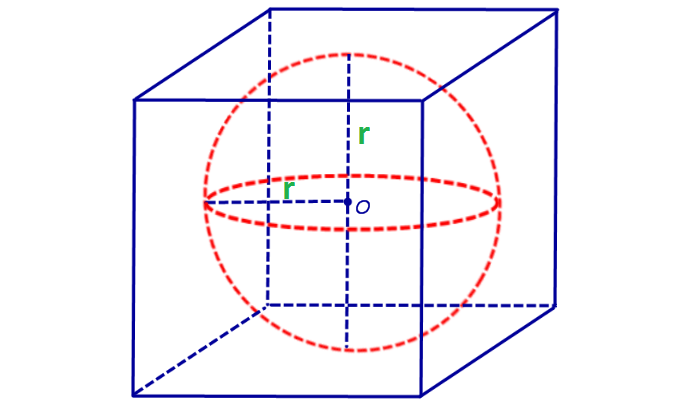
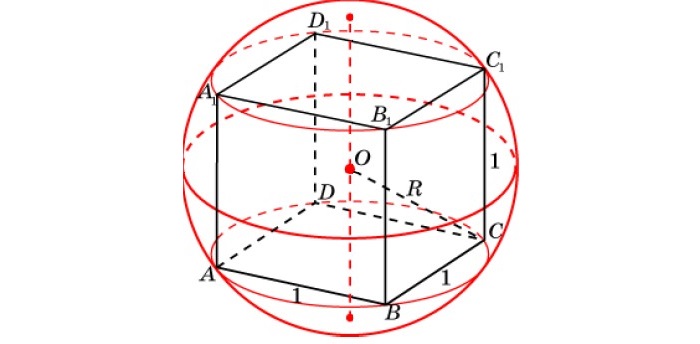
Предположим, что а – длина стороны куба, а d — диагональ, тогда:

Диагональ куба – это отрезок, который соединяет 2 вершины, которые симметричны относительно центра

Свойства куба.

перпендикулярно четырём его главным диагоналям.

совмещены с 4-мя вершинами куба и каждое из шести ребер тетраэдра принадлежат граням куба. В 1-м

случае каждая вершина тетраэдра принадлежит граням трехгранного угла, вершиной совпадающего с одной

из вершин куба. Во 2-м случае ребра тетраэдра, которые попарно скрещиваются принадлежат попарно

противоположным граням куба. Такой тетраэдр будет правильным, а его объём будет составлять треть от

6-ти гранях куба, следующие 24 ребра располагаются внутри куба. Каждая из 12 вершин икосаэдра

располагается на 6-ти гранях куба.

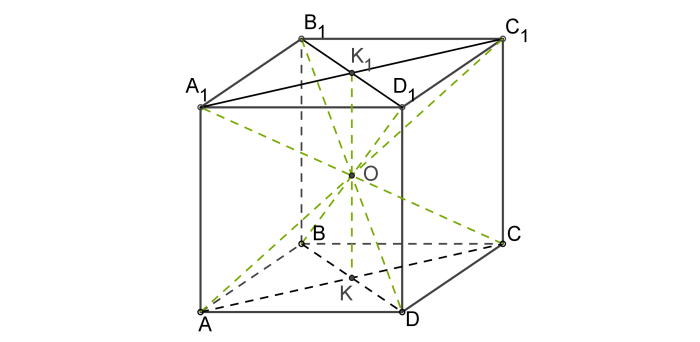
Элементы симметрии куба.

Ось симметрии куба может пролегать или сквозь середины ребер, которые

параллельны, не принадлежащих одной из граней, или сквозь точку

пересечения диагоналей противолежащих граней. Центром симметрии

куба будет точка пересечения диагоналей куба.

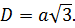
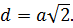
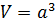
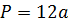
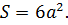
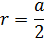
Сквозь центр симметрии куба проходят 9 осей симметрии.

Плоскостей симметрии у куба тоже 9, они пролегают или

через противолежащие ребра (таких плоскостей 6), или

через середины противолежащих ребер (таких 3).

Источник

Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.

Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:

многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;

прямая призма, все грани которой есть квадраты;

прямоугольный параллелепипед, все рёбра которого равны.

Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.

Элементы куба

Основными элементами многогранника считаются грани, рёбра, вершины.

Грань

Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.

Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.

Грани куба попарно перпендикулярны, являются квадратами, равны между собой.

Ребро

Линии пересечения сторон называются рёбрами.

Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.

Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.

Вершина

Точки пересечения рёбер называются вершинами. Их число равно восьми.

Центр грани

Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.

Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.

Центр куба

Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.

Это есть центр симметрии куба.

Ось куба

Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.

Диагональ куба

Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.

Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:

Формула доказывается с помощью дважды применённой теоремы Пифагора.

Все диагонали куба равны между собой и точкой пересечения делятся пополам.

Диагональ грани куба

Длина диагонали грани в √2 раз больше ребра, то есть:

Эта формула доказывается также с помощью теоремы Пифагора.

Объем куба

Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:

Периметр куба

Сумма длин всех рёбер равна:

Площадь поверхности

Сумма площадей всех граней называется площадью поверхности куба. Она равна:

Сфера, вписанная в куб

Такая сфера имеет центр, совпадающий с центром куба.

Радиус равен половине ребра:

Сфера, описанная вокруг куба

Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:

Координаты вершин куба

В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.

Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:

Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).

Свойства куба

Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.

Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.

у куба все грани равны, являются квадратами;

у куба все рёбра равны;

один центр и несколько осей симметрии.

Источник

Что такое сечение куба

Правила построения сечений многогранников:

1) проводим прямые через точки, лежащие в одной плоскости;

2) ищем прямые пересечения плоскости сечения с гранями многогранника, для этого

а) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);

б) параллельные грани плоскость сечения пересекает по параллельным прямым.

Примеры построения сечений:

Рассмотрим прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Построим сечение, проходящее через точки M, N, L.

Соединим точки M и L, лежащие в плоскости AA₁D₁D.

Пересечем прямую ML ( принадлежащую сечению) с ребром A₁D₁, они лежат в одной плоскости AA₁D₁D. Получим точку X₁.

Точка X₁ лежит на ребре A₁D₁, а значит и плоскости A₁B₁C₁D₁, соединим ее сточкой N, лежащей в этой же плоскости.

X₁ N пересекается с ребром A₁B₁ в точке К.

Соединим точки K и M, лежащие в одной плоскости AA₁B₁B.

Найдем прямую пересечения плоскости сечения с плоскостью DD₁C₁C:

пересечем прямую ML (принадлежащую сечению) с ребром DD₁, они лежат в одной плоскости AA₁D₁D, получим точку X₂;

пересечем прямую KN (принадлежащую сечению) с ребром D₁C₁, они лежат в одной плоскости A₁B₁C₁D₁, получим точку X₃;

Рассмотрим ту же самую задачу на построение сечения, но воспользуемся свойством параллельных плоскостей. Это облегчит нам построение сечения.

.

Соединим точки M и L, лежащие в плоскости AA₁D₁D.

.

Через точку N, проведем прямую NT параллельную прямой ML. Прямые NT и ML лежат в параллельных плоскостях по свойству параллелепипеда.

.

Пересечем прямую ML ( принадлежащую сечению) с ребром A₁D₁, они лежат в одной плоскости AA₁D₁D. Получим точку X₁.

.

Точка X₁ лежит на ребре A₁D₁, а значит и плоскости A₁B₁C₁D₁, соединим ее сточкой N, лежащей в этой же плоскости.

X₁ N пересекается с ребром A₁B₁ в точке К.

.

Соединим точки K и M, лежащие в одной плоскости AA₁B₁B.

.

Проведем прямую TP через точку T, параллельно прямой KM ( они лежат в параллельных плоскостях).

.

Соединим точки P и L ( они лежат в одной плоскости).

.

Источник

• ← что такое если месячные идут 2 раза в месяц у подростков
• кот прокусил вену на руке что делать →