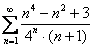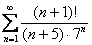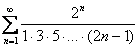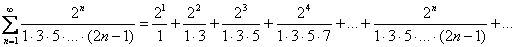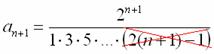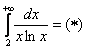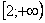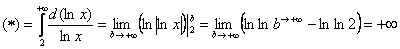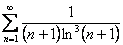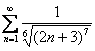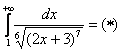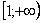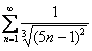что такое ряд сходится
Определение и свойства сходящихся рядов
Сходящийся числовой ряд и его сумма.
Выражение \(a_ <1>+ a_ <2>+ \ldots + a_
$$
S_
$$
Ряд
$$
\sum_
$$
называется сходящимся, если последовательность его частичных сумм \(\
$$
\lim_
$$
Число \(S\), определяемое условиями \eqref
$$
\sum_
$$
Если последовательность \(\
\(\vartriangle\) Используя формулу для суммы \(n\) первых членов геометрической прогрессии, получаем
$$
S_
$$
Так как \(q^
Доказать, что если при всех \(n \in N\) выполняется равенство
$$
a_
$$
и существует конечный
$$
\lim_
$$
то ряд \eqref
$$
\sum_
$$
\(\vartriangle\) Используя условие \eqref
Найти сумму ряда \eqref
\(\vartriangle\) Так как
$$
a_
$$
то последовательность \(\
$$
\sum_
$$
Необходимое условие сходимости ряда.
\(\circ\) Так как ряд \eqref
Таким образом, соотношение \eqref
Доказать, что ряд \(\displaystyle\sum_
\(\vartriangle\) Так как \(\displaystyle\frac<1><\sqrt
Условие \eqref
Доказать, что ряд
$$
\sum_
$$
расходится.
\(\vartriangle\) Докажем, что
$$
\sin n\alpha \nrightarrow 0\ \mbox<при>\ n \rightarrow \infty,\label
$$
Предположим, что \(\sin n\alpha \rightarrow 0\) при \(n \rightarrow \infty\). Тогда \(\sin (n + 1)\alpha \rightarrow 0\) при \(n \rightarrow \infty\), то есть \(\sin n\alpha \cos \alpha + \cos n\alpha \sin \alpha \rightarrow 0\), откуда следует, что \(\cos n\alpha \rightarrow 0\) при \(n \rightarrow \infty\), так как \(\sin \alpha \neq 0\). Итак, если \(\sin n\alpha \rightarrow 0\), то \(\cos n\alpha \rightarrow 0\) при \(n \rightarrow \infty\), что невозможно, так как \(\sin^ <2>n\alpha + \cos^ <2>n\alpha = 1\).
Таким образом, для ряда \eqref
Свойства сходящихся рядов.
Если ряды \(\displaystyle\sum_
$$
\sum_
$$
сходятся, а их суммы равны соответственно \(S\) и \(\sigma\), то при любых \(\lambda, \mu \in \mathbb
$$
\sum_
$$
а его сумма равна
$$
\tau = \lambda S + \mu\sigma.\label
$$
\(\circ\) Пусть \(S_
Если сходится ряд \(\displaystyle\sum_
$$
\sum_
$$
который называют \(m\)-м остатком ряда \(\displaystyle\sum_
\(\circ\) Пусть \(S_
$$
S_
$$
Если ряд \eqref
Обратно: если \(m\) фиксировано и существует конечный \(\displaystyle\lim_
Согласно свойству 2 отбрасывание конечного числа членов ряда или добавление конечного числа членов к данному ряду не влияет на его сходимость.
Если ряд \(\displaystyle\sum_
$$
\sum_
$$
полученный группировкой членов ряда \(\displaystyle\sum_
\(\circ\) Пусть \(b_ <1>= a_ <1>+ a_ <2>+ \ldots + a_
Критерий Коши сходимости ряда.
Для сходимости ряда \eqref
$$
\forall \varepsilon > 0\ \exists N_<\varepsilon>: \forall n \geq N_<\varepsilon>, \forall p \in \mathbb
\(\circ\) Так как \(a_
Если условие \eqref
$$
\exists \varepsilon_ <0>> 0: \forall k \in \mathbb
$$
то ряд \eqref
Доказать, что гармонический ряд
$$
\sum_
$$
расходится.
\(\vartriangle\) Для любого \(k \in \mathbb
Ряды с комплексными членами.
Последовательность комплексных чисел \(\
$$
\lim_
$$
где \(|z|\) — модуль комплексного числа \(z\). В этом случае пишут \(\displaystyle\lim_
Если \(z_
Ряд с комплексными членами
$$
\sum_
$$
называют сходящимся, если существует
$$
\lim_
$$
где \(S \in \mathbb
Числовые ряды: определения, свойства, признаки сходимости, примеры, решения
Данная статья представляет собой структурированную и подробную информацию, которая может пригодиться во время разбора упражнений и задач. Мы рассмотрим тему числовых рядов.
Данная статья начинается с основных определений и понятий. Далее мы стандартные варианты и изучим основные формулы. Для того, чтобы закрепить материал, в статье приведены основные примеры и задачи.
Базовые тезисы
a k является общим или k –ым членом ряда.
Определения, рассмотренные выше, помогут вам для решения большинства примеров и задач.
Для того, чтобы дополнить определения, необходимо доказать определенные уравнения.
Мы доказали, что числовой ряд сходится.
Мы доказали, что числовой ряд расходится.
Ряд ∑ k = 1 ∞ b k знакопеременный, так как в нем множество чисел, отрицательных и положительных.
Второй вариант ряд – это частный случай третьего варианта.
Приведем примеры для каждого случая соответственно:
Для третьего варианта также можно определить абсолютную и условную сходимость.
Знакочередующийся ряд ∑ k = 1 ∞ b k абсолютно сходится в том случае, когда ∑ k = 1 ∞ b k также считается сходящимся.
Подробно разберем несколько характерных вариантов
Знакопеременный ряд ∑ k = 1 ∞ b k считается условно сходящимся в том случае, если ∑ k = 1 ∞ b k – расходящийся, а ряд ∑ k = 1 ∞ b k считается сходящимся.
Особенности сходящихся рядов
Проанализируем свойства для определенных случаев
Разложим исходный вариант:
Необходимое условие для определения, является ли ряд сходящимся
Проверим исходное выражение на выполнение условия lim n → + ∞ n 2 1 + n = lim n → + ∞ n 2 n 2 1 n 2 + 1 n = lim n → + ∞ 1 1 n 2 + 1 n = 1 + 0 + 0 = + ∞ ≠ 0
Как определить сходимость знакоположительного ряда.
Если постоянно пользоваться указанными признаками, придется постоянно вычислять пределы. Данный раздел поможет избежать сложностей во время решения примеров и задач. Для того, чтобы определить сходимость знакоположительного ряда, существует определенное условие.
Как сравнивать ряды
Существует несколько признаков сравнения рядов. Мы сравниваем ряд, сходимость которого предлагается определить, с тем рядом, сходимость которого известна.
Первый признак
Для того, чтобы закрепить полученный материал, детально рассмотрим пару типичных вариантов.
Второй признак
Согласно второму признаку можно определить, что сходящийся ряд ∑ k = 1 ∞ 1 k 3 означается, что первоначальный вариант также сходится.
Согласно приведенным выше тезисам, расходящийся ряд влечет собой расходимость исходного ряда.
Третий признак
Рассмотрим третий признак сравнения.
Признак Даламбера
Признак Даламбера справедлив в том случае, если предел бесконечен.
Определить, является ряд сходящимся или расходящимся ∑ k = 1 ∞ 2 k + 1 2 k по признаку Даламбера.
Необходимо проверить, выполняется ли необходимое условие сходимости. Вычислим предел, воспользовавшись правилом Лопиталя: lim k → + ∞ 2 k + 1 2 k = » open=» ∞ ∞ = lim k → + ∞ 2 k + 1 ‘ 2 k ‘ = lim k → + ∞ 2 2 k · ln 2 = 2 + ∞ · ln 2 = 0
Мы можем увидеть, что условие выполняется. Воспользуемся признаком Даламбера: lim k → + ∞ = lim k → + ∞ 2 ( k + 1 ) + 1 2 k + 1 2 k + 1 2 k = 1 2 lim k → + ∞ 2 k + 3 2 k + 1 = 1 2 1
Ряд является сходящимся.
Следовательно, ряд является расходящимся.
Радикальный признак Коши
Данный признак может быть использован в примерах, которые легко определить. Случай будет характерным тогда, когда член числового ряда – это показательно степенное выражение.
Для того, чтобы закрепить полученную информацию, рассмотрим несколько характерных примеров.
Определить, является ли знакоположительный ряд ∑ k = 1 ∞ 1 ( 2 k + 1 ) k на сходящимся.
Интегральный признак Коши
, то в случае, если несобственный интеграл ∫ a + ∞ f ( x ) d x является сходящимся, то рассматриваемый ряд также сходится. Если же он расходится, то в рассматриваемом примере ряд тоже расходится.
При проверке убывания функции можно использовать материал, рассмотренный на предыдущих уроках.
Рассмотреть пример ∑ k = 2 ∞ 1 k · ln k на сходимость.
Согласно полученным результатам, исходный пример расходится, так как несобственный интеграл является расходящимся.
Признак Раабе
Данный способ определения можно использовать в том случае, если описанные выше техники не дают видимых результатов.
Исследование на абсолютную сходимость
Расходимость знакопеременных рядов
Если ряд ∑ k = 1 ∞ b k – расходящийся, то соответствующий знакопеременный ряд ∑ k = 1 ∞ b k либо расходящийся, либо условно сходящийся.
Признаки для условной сходимости
Признак Лейбница
Ряд условно сходится.
Признак Абеля-Дирихле
∑ k = 1 + ∞ u k · v k сходится в том случае, если < u k >не возрастает, а последовательность ∑ k = 1 + ∞ v k ограничена.
Признаки сходимости рядов.
Признак Даламбера. Признаки Коши
Работайте, работайте – а понимание придёт потом
Ж.Л. Даламбер
Всех поздравляю с началом учебного года! Сегодня 1 сентября, и я решил в честь праздника познакомить читателей с тем, что вы давно с нетерпением ждали и жаждали узнать – признаками сходимости числовых положительных рядов. Праздник Первое сентября и мои поздравления всегда актуальны, ничего страшного, если на самом деле за окном лето, вы же сейчас в третий раз пересдаете экзамен учитесь, если зашли на эту страничку!
Для тех, кто только начинает изучать ряды, рекомендую для начала ознакомиться со статьей Числовые ряды для чайников. Собственно, данная телега является продолжением банкета. Итак, сегодня на уроке мы рассмотрим примеры и решения по темам:
Одним из распространенных признаков сравнения, который встречается в практических примерах, является признак Даламбера. Признаки Коши встречаются реже, но тоже весьма популярны. Как всегда, постараюсь изложить материал просто, доступно и понятно. Тема не самая сложная, и все задания в известной степени трафаретны.
Признак сходимости Даламбера
Жан Лерон Даламбер – это знаменитый французский математик 18-го века. Вообще, Даламбер специализировался на дифференциальных уравнениях и на основании своих исследований занимался баллистикой, чтобы у Его Величества лучше летали пушечные ядра. Заодно и про числовые ряды не забыл, не зря потом шеренги наполеоновских войск так четко сходились и расходились.
Перед тем как сформулировать сам признак, рассмотрим важный вопрос:
Когда нужно применять признак сходимости Даламбера?
Сначала начнем с повторения. Вспомним случаи, когда нужно применять самый ходовой предельный признак сравнения. Предельный признак сравнения применяется тогда, когда в общем члене ряда:
1) В знаменателе находится многочлен.
2) Многочлены находятся и в числителе и в знаменателе.
3) Один или оба многочлена могут быть под корнем.
4) Многочленов и корней, разумеется, может быть и больше.
Основные же предпосылки для применения признака Даламбера следующие:
1) В общий член ряда («начинку» ряда) входит какое-нибудь число в степени, например, 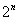
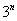
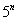
2) В общий член ряда входит факториал. С факториалами мы скрестили шпаги ещё на уроке Числовая последовательность и её предел. Впрочем, не помешает снова раскинуть скатерть-самобранку: 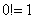
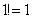
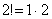
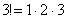
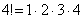
… 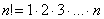
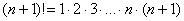
…
! При использовании признака Даламбера нам как раз придется расписывать факториал подробно. Как и в предыдущем пункте, факториал может располагаться вверху или внизу дроби.
3) Если в общем члене ряда есть «цепочка множителей», например, 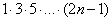
Вместе со степенями или (и) факториалами в начинке ряда часто встречаются многочлены, это не меняет дела – нужно использовать признак Даламбера.
Кроме того, в общем члене ряда может встретиться одновременно и степень и факториал; может встретиться два факториала, две степени, важно чтобы там находилось хоть что-то из рассмотренных пунктов – и это как раз предпосылка для использования признака Даламбера.
Признак Даламбера: Рассмотрим положительный числовой ряд 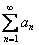
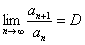
а) При 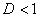
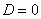
б) При 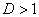
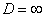
в) При 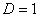
У кого до сих пор проблемы с пределами или недопонимание пределов, обратитесь к уроку Пределы. Примеры решений. Без понимания предела и умения раскрывать неопределенность 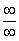
А сейчас долгожданные примеры.
Исследовать ряд на сходимость 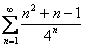
Мы видим, что в общем члене ряда у нас есть 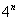
Используем признак Даламбера:

Таким образом, исследуемый ряд сходится.
(1) Составляем отношение следующего члена ряда к предыдущему: 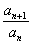
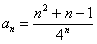
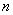
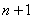
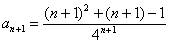
(2) Избавляемся от четырехэтажности дроби. При определенном опыте решения этот шаг можно пропускать.
(3) В числителе раскрываем скобки. В знаменателе выносим четверку из степени.
(4) Сокращаем на 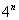
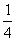
(5) Неопределенность 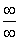
(6) Почленно делим числители на знаменатели, и указываем слагаемые, которые стремятся к нулю.
(7) Упрощаем ответ и делаем пометку, что 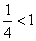
В рассмотренном примере в общем члене ряда у нас встретился многочлен 2-й степени. Что делать, если там многочлен 3-й, 4-й или более высокой степени? Дело в том, что если дан многочлен более высокой степени, то возникнут трудности с раскрытием скобок. В этом случае можно применять «турбо»-метод решения.
Возьмём похожий ряд и исследуем его на сходимость
Сначала полное решение, потом комментарии:
Используем признак Даламбера: 
Таким образом, исследуемый ряд сходится.
(1) Составляем отношение 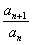
(2) Избавляемся от четырехэтажности дроби.
(3) Рассмотрим выражение 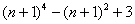
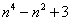
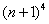
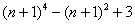
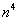
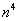
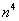
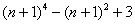
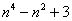
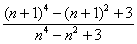
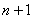
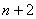
На самом деле, такую «халтуру» можно было провернуть и в Примере № 1, но для многочлена 2-й степени такое решение смотрится всё-таки как-то несолидно. Лично я поступаю так: если есть многочлен (или многочлены) первой или второй степени, я использую «длинный» способ решения Примера 1. Если попадается многочлен 3-й и более высоких степеней, я использую «турбо»-метод по образцу Примера 2.
Исследовать ряд на сходимость
Полное решение и образец оформления в конце урока
Рассмотрим типовые примеры с факториалами:
Исследовать ряд на сходимость
В общий член ряда входит и степень, и факториал. Ясно, как день, что здесь надо использовать признак Даламбера. Решаем.
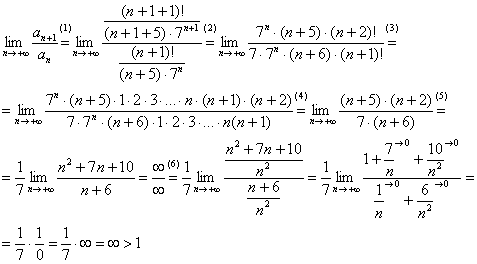
Таким образом, исследуемый ряд расходится.
(1) Составляем отношение 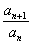
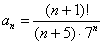
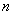
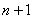
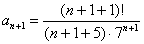
(2) Избавляемся от четырехэтажности дроби.
(3) Отщипываем семерку от степени. Факториалы расписываем подробно. Как это сделать – см. начало урока или статью о числовых последовательностях.
(4) Сокращаем всё, что можно сократить.
(5) Константу 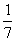
(6) Неопределенность 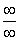
Исследовать ряд на сходимость
Полное решение и образец оформления в конце урока
Исследовать ряд на сходимость
Иногда встречаются ряды, которые в своей начинке содержат «цепь» множителей, этот тип ряда мы еще не рассматривали. Как исследовать ряд с «цепочкой» множителей? Использовать признак Даламбера. Но сначала для понимания происходящего распишем ряд подробно:
Из разложения мы видим, что у каждого следующего члена ряда добавляется дополнительный множитель в знаменателе, поэтому, если общий член ряда 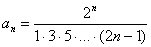
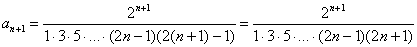
Примерный образец решения может выглядеть так:
Используем признак Даламбера:
Таким образом, исследуемый ряд сходится.
Радикальный признак Коши
Огюстен Луи Коши – еще более знаменитый французский математик. Биографию Коши вам может рассказать любой студент технической специальности. В самых живописных красках. Не случайно эта фамилия высечена на первом этаже Эйфелевой башни.
Признак сходимости Коши для положительных числовых рядов чем-то похож на только что рассмотренный признак Даламбера.
Радикальный признак Коши: Рассмотрим положительный числовой ряд 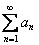
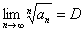
а) При 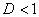
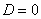
б) При 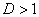
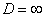
в) При 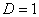
Когда нужно использовать радикальный признак Коши? Радикальный признак Коши обычно использует в тех случаях, когда корень 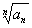
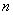
Исследовать ряд на сходимость
Мы видим, что дробь полностью находится под степенью, зависящей от «эн», а значит, нужно использовать радикальный признак Коши: 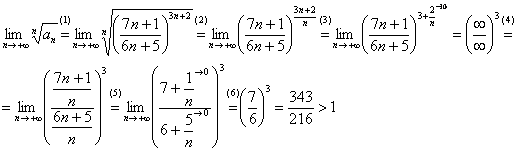
Таким образом, исследуемый ряд расходится.
(1) Оформляем общий член ряда под корень.
(2) Переписываем то же самое, только уже без корня, используя свойство степеней 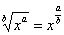
(3) В показателе почленно делим числитель на знаменатель, указывая, что 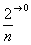
(4) В результате у нас получилась неопределенность 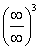
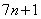
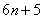
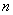
(5) Выполняем почленное деление, и указываем слагаемые, которые стремятся к нулю.
(6) Доводим ответ до ума, помечаем, что 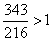
А вот более простой пример для самостоятельного решения:
Исследовать ряд на сходимость
И еще пара типовых примеров.
Полное решение и образец оформления в конце урока
Исследовать ряд на сходимость 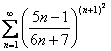
Используем радикальный признак Коши: 
Таким образом, исследуемый ряд сходится.
(1) Помещаем общий член ряда под корень.
(2) Переписываем то же самое, но уже без корня, при этом раскрываем скобки, используя формулу сокращенного умножения: 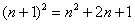
(3) В показателе почленно делим числитель на знаменатель и указываем, что 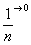
(4) Получена неопределенность вида 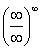
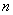
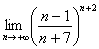
(5) Собственно выполняем почленное деление и указываем, какие слагаемые у нас стремятся к нулю.
(6) Неопределенность устранена, у нас остался простейший предел: 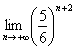
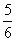
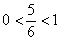
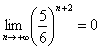
Если 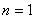
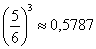
Если 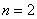
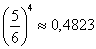
Если 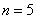
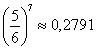
Если 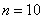
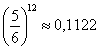
Если 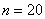
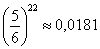
… и т.д. до бесконечности – то есть, в пределе:
Прямо таки бесконечно убывающая геометрическая прогрессия на пальцах =)
! Никогда не используйте этот приём в качестве доказательства! Ибо если что-то очевидно, то это ещё не значит, что это правильно.
(7) Указываем, что 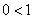
Исследовать ряд на сходимость
Это пример для самостоятельного решения.
Иногда для решения предлагается провокационный пример, например: 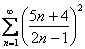
Интегральный признак Коши
Или просто интегральный признак. Разочарую тех, кто плохо усвоил материал первого курса. Для того чтобы применять интегральный признак Коши необходимо более или менее уверенно уметь находить производные, интегралы, а также иметь навык вычисления несобственного интеграла первого рода.
В учебниках по математическому анализу интегральный признак Коши дан математически строго, но слишком уж поморочено, поэтому я сформулирую признак не слишком строго, но понятно:
Рассмотрим положительный числовой ряд 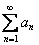
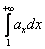
И сразу примеры для пояснения:
Исследовать ряд на сходимость
Почти классика. Натуральный логарифм и какая-нибудь бяка.
Основной предпосылкой использования интегрального признака Коши является тот факт, что в общем члене ряда содержатся множители, похожие на некоторую функцию и её производную. Из темы Производная вы наверняка запомнили простейшую табличную вещь: 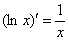
Как использовать интегральный признак? Сначала берем значок интеграла и переписываем со «счётчика» ряда верхний и нижний пределы: 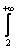
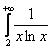
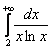
Теперь нужно вычислить несобственный интеграл 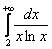
1) Если выяснится, что интеграл 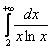
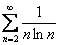
2) Если выяснится, что интеграл 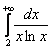
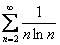
Повторюсь, если материал запущен, то чтение параграфа будет трудным и малопонятным, поскольку применение признака по сути дела сводится к вычислению несобственного интеграла первого рода.
Полное решение и оформление примера должно выглядеть примерно так:
Используем интегральный признак:
Подынтегральная функция непрерывна на
Таким образом, исследуемый ряд расходится вместе с соответствующим несобственным интегралом.
Исследовать ряд на сходимость
Решение и образец оформления в конце урока
В рассмотренных примерах логарифм также мог находиться под корнем, это не изменило бы способа решения.
И еще два примера на закуску
Исследовать ряд на сходимость
По общим «параметрам» общий член ряда подходит для использования предельного признака сравнения. Нужно всего лишь раскрыть скобки 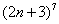
сразу сдать на кандидата предельно сравнить данный ряд со сходящимся рядом 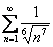
Поэтому мы используем интегральный признак Коши:
Подынтегральная функция непрерывна на
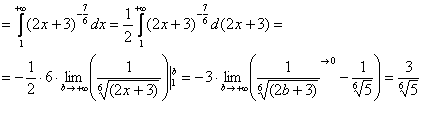
Получено конечное число, значит, исследуемый ряд сходится вместе с соответствующим несобственным интегралом.
! Примечание: полученное число 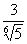
Исследовать ряд на сходимость
Решение и образец оформления в конце урока, который подходит к концу.
Да. Возможно, у некоторых возник вопрос, почему я начал этот урок с таким энтузиазмом? Всё просто – начался учебный год, а мне не нужно на учебу. Я столько мучался =( Что даже не устал в заключительных аккордах этой статьи.
В целях окончательного и бесповоротного усвоения темы числовых рядов посетите урок Знакочередующиеся ряды. Признак Лейбница. Примеры решений.
Пример 3: Используем признак Даламбера: 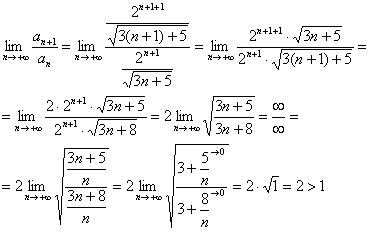
Таким образом, исследуемый ряд расходится.
Примечание: Можно было использовать и «турбо»-метод решения: сразу обвести карандашом отношение 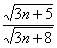
Пример 5: Используем признак Даламбера: 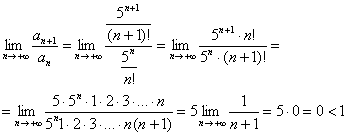
Таким образом, исследуемый ряд сходится.
Пример 8: Используем радикальный признак Коши: 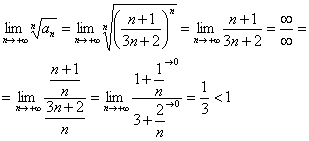
Таким образом, исследуемый ряд сходится.
Пример 10: Используем радикальный признак Коши: 
Таким образом, исследуемый ряд расходится.
Примечание: Здесь основание степени 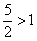
Пример 12: Используем интегральный признак:.
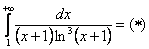
Подынтегральная функция непрерывна на 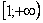

Получено конечное число, значит, исследуемый ряд сходится вместе с соответствующим несобственным интегралом.
Пример 14: Используем интегральный признак:
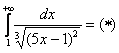
Подынтегральная функция непрерывна на 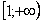

Таким образом, исследуемый ряд расходится вместе с соответствующим несобственным интегралом.
Примечание: Ряд 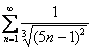
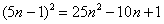
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5