что такое разность широт
Географические координаты, разность широт и разность долгот



Положение какой-либо точки на поверхности Земли определяются географическими координатами широтой (Latitude) и долготой (Longitude).. Прямая, проходящая через точку на земной поверхности (точка А рис.4) к центру Земли совпадает с отвесной линией.
|
|
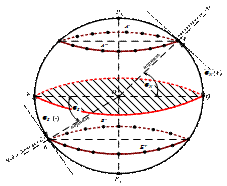
Географическая широта (φ) точки (рис.4,а)– это угол с вершиной в центре Земли между отвесной линией, проходящей через данную точку, и плоскость земного экватора. Она измеряется дугой меридиана от экватора до параллели данной точки от 0 о (на экваторе) до 90 о (на полюсе). Если точка находится в северном полушарии, то широте приписывается наименование N, если в южном, то S.
Северная широта имеет условный знак «+», а южная «–»
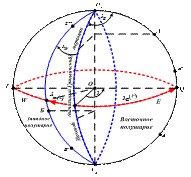
Географическая долгота (λ) места (рис.4,б)– – это двугранный угол между плоскостями Гринвичского меридиана и меридиана данной точки. Долгота измеряется дугой экватора от Гринвичского меридиана до меридиана точки от 0 о до 180 о в сторону оста или веста. Если точка находится в восточном полушарии, ей присваивается наименование E, а если в западном W
Восточная долгота имеет условный знак «+», а западная – «–».
Полюса являются особыми точками, где долгота не определена.
Широта и долгота измеряются в градусах, минутах и их долях.

В полярной системе координат место точки на поверхности Земли определяется по направлению и расстоянию относительно исходной точки. Как правило, эта система используется при определении положения судна относительно другого объекта или наоборот.
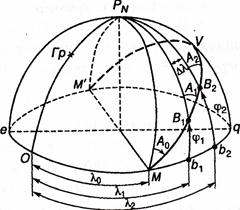
Если судно находится первоначально в точке А с координатами (φ1 λ1) и следует в точку В с координатами (φ2 λ2) образуется разность широт и разность долгот(рис.6).
Одна из основных задач мореплавания в целом и навигации в частности заключается в оптимизации путей судов. Обычно предпочтение отдается плаванию по кратчайшему расстоянию.
На эллипсоиде кратчайшим расстоянием является геодезическая линия. Это сложная линия двоякой кривизны рассматривается в курсе высшей геодезии. Процесс ее расчета и прокладки на карте достаточно труден.
На практике решение этой проблемы упрощают, рассматривая кратчайшее расстояния между двумя точками на шаре. При необходимости решения задач на эллипсоиде, пользуются поправками на сферичность Земли из «Мореходных таблиц».
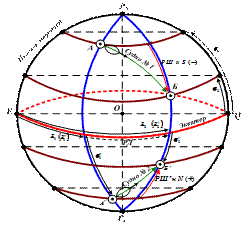
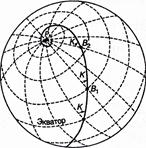
Кратчайшим расстоянием на шаре между двумя точками является дуга большого круга (ДБК), называемая ортодромией (great circle). В переводе с греческого языка ортос – прямой, дромос – проход, бег. Ортодромия пересекает меридианы под разными углами(рис. 7). Поэтому, при плавании по ортодромии приходится постоянно менять курс судна. ДБК достигает максимальной широты в точке V, которая называется вертекс.
Свойства ДБК будут рассматриваться в более позднем курсе, но здесь примем без доказательств свойства ортодромии:
1. Меридиан вертекса является осью симметрии ортодромии, т.е. ортодромия дважды пересекает каждый меридтиан.
2. Если угол между меридианом и ортодромией А, то при А0 = 90 о (270 о ) ортодромия совпадает с экватором, при А0 = 0 о (180 о ) ортодромия совпадает с меридианом.
3. Ортодромия пересекает каждый меридиан в одной и той же точке.
4. Ортодромия пересекает все меридианы под различными углами.
Плавание по ортодромии осуществляют на больших трансокеанских переходах.
Для практики мореплавания весьма удобна линия пути, которая пересекает все меридианы под одним и тем же углом. По этой линии можно вести судно не изменяя при этом курса. Такая линия называется локсодромией (loxodromec or Rhumb line). В переводе с греческого языка локсос – косой, дромос – проход, бег. (рис.8)
Так как меридианы не параллельны, то и локсодромия, пересекающая их под равными углами К не прямая линия. Она представляет собой логарифмическую спираль – линию двоякой кривизны, которая стремится к полюсу.
1. При К = 0 о (180 о ) локсодромия совпадает с меридианом;
2. При К= 90 о (270 о ) локсодромия совпадает с параллелью. В частном случае при φ2= φ1=0 о локсодромия совпадает с экватором;
3. Локсодромия пересекает каждый меридиан бесчисленное количество раз, но каждый раз в новой широте.
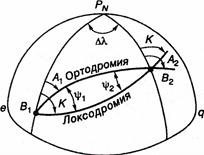
В практике судовождения широко используются и ортодромия и локсодромия. поэтому возникает необходимость перехода от ортодромических направлений к локсодромическим и наоборот.
Угол между ортодромией и локсодромией, проходящими через две заданные точки называется ортодромической поправкой.
На расстоянии до 500 миль можно считать ортодромию и локсодромию расположенными симметрично, и тогда ψ1 = ψ2 = ψ.
Если расстояние между точками В1 и В2 больше 500 миль, то ψ1≠ψ2
В этом случае необходим непосредственный расчет ортодромической поправки как разности направлений локсодромии и ортодромии по формуле:
Для облегчения расчета ортодромической поправки на малых расстояниях расчет производится с помощью Мореходных таблиц.
Из сказанного следует:
1. Из-за сложности геометрии геоида, затрудняющей решение навигационных задач, для решения задач навигации используют эллипсоид вращения – тело, полученное в результате вращения эллипсоида вокруг малой оси.
2. Для картографических и геодезических расчетов в определенных районах земли необходимо иметь эллипсоид, поверхность которого максимально совпадала с поверхностью данного района. Это референц-эллипсоид. Очевидно, что в конкретном районе это будет различный референц-эллипсоид.
3. Для решения специальных навигационных задач, например задач определения места судна с помощью глобальных навигационных систем, применяются специальные, международные референц-элипсоиды WGS-72 и WGS-84.
4. Положение какой-либо точки на поверхности Земли определяются географическими координатами широтой (Latitude) и долготой (Longitude).
5. Разница в координатах двух точек определяется разностью широт и разностью долгот.
Контрольные вопросы к лекции
1. Какова реальная форма Земли?
2. Какие ограничения накладывает нерегулярность поверхности геоида?
3. Что такое земной эллипсоид?
4. Что такое референц-эллипсоид?
5. Что такое земная ось?
6. Что такое географические или истинные полюса?
7. Что такое большой круг?
8. Что такое параллель?
9. Что такое экватор?
10. Что такое географический, или истинный меридиан?
11. Что такое меридиан наблюдателя?
12. Что такое нулевой меридиан?
13. Что такое отвесная линия?
14. Что такоегеографическая широта?
15. Что такоегеографическая долгота?
16. Что такоеразность широт (РШ)?
17. Что такоеразность долгот (РД)?
18. Что такое ортодромия?
Рассмотрено и утверждено на заседании кафедры Судовождения и морской безопасности.
§ 2. ГЕОГРАФИЧЕСКИЕ КООРДИНАТЫ
Широта и долгота
Положение каждой точки на земной поверхности определяют ее координатами: широтой и долготой (рис. 3).
Широтой называется угол, образованный отвесной линией, проходящей через заданную точку на поверхности Земли, и плоскостью экватора (на рис. 3 для точки М угол МОС).
В какой бы точке на земном шаре ни находился наблюдатель, его сила тяжести всегда будет направлена к центру Земли. Такое направление называется отвесным, или вертикальным.
Широта измеряется дугой меридиана от экватора до параллели данной точки в пределах от 0 до 90° и обозначается буквой ф. Таким образом, географическая параллель eabq является геометрическим местом точек, имеющих одну и ту же широту.
В зависимости от того, в каком полушарии находится точка, широте присваивают наименование северная (N) или южная (S).
В зависимости от того, в каком полушарии находится точка, долгота называется восточной (O st ) или западной (W).
Разность широт и разность долгот
Во время плавания судно непрерывно изменяет свое место на поверхности Земли, следовательно, изменяются и его координаты. Величина изменения широты Аф, получающаяся при переходе судна из пункта отхода MI в пункт прихода С1, называется разностью широт (РШ). РШ измеряется дугой меридиана между параллелями пунктов отхода и прихода M1C1 (рис. 4).
Наименование РШ зависит от расположения параллели пункта прихода относительно параллели пункта отхода. Если параллель пункта прихода располагается севернее параллели пункта отхода, то РШ считается сделанной к N, а если южнее — то к S.
где φ1 — широта пункта отхода;
φ2 — широта пункта прихода;
λ1 — долгота пункта отхода;
λ2 — долгота пункта прихода.
При этом северные широты и восточные долготы считаются положительными и им приписывается знак плюс, а южные широты и западные долготы — отрицательными и им приписывается знак минус. При решении задач по формулам (1) и (2) в случае положительных результатов РШ она будет сделана к N, а РД — к O st (см. пример 1), а в случае отрицательных результатов РШ она будет к S, а РД — к W (см. пример 2). При получении результата РД более 180° с отрицательным знаком нужно прибавить 360° (см. пример 3), а если результат РД больше 180° с положительным знаком, надо вычесть 360° (см. пример 4).
Пример 2. Известны: φ1 = 72°50′ N; λ1 = :80°56’O st : φ2 = 62 O st 49’N;
Пример 3. Известны: φ1 = 45°10′ N; λ1 = 172°10′ O st ; φ2 = 50°15’S; λ2 = 175°15’W.
С помощью формул (1) и (2) по известным координатам пункта отхода (φ1 и λ1) и сделанным судном разности широт (РШ) и разности долгот (РД) можно определить координаты пункта прихода (φ2, λ2).
Начались испытания ледокола «Арктика» после замены электродвигателя
Источник рассказал, когда возобновятся испытания «Циркона» с подлодки
Австралия договорилась с США и Великобританией о доступе к ядерным технологиям
Во Владивостоке начались швартовные испытания корвета «Резкий»
Путь судна, разница широт, разница долгот.
Путь судна определяется разницей широт и разницей долгот.
Разность широт (РШ) двух точек на земной поверхности измеряется дугой меридиана, заключенной между параллелями этих точек.
Если широты пунктов отхода и прихода одноименные (в одном полушарии), то РШ численно равна разности большей и меньшей широт этих точек.
Если разные полушария, РШ = сумме широт двух точек.
Наибольшее значение = 180° – от полюса до полюса.
Если судно шло на север, РШ имеет знак +, если на юг – знак –.
Разность долгот (РД) 2 точек земной поверхности измеряется меньшей из дуг экватора, заключенных между меридианами этих точек.
Если долготы пунктов отхода и прихода одноименные (в одном полушарии), то РШ численно равна разности большей и меньшей долгот этих точек.
Если разные полушария, РШ = сумме долгот двух точек.
РД не может быть больше 180°. Если в результате расчета превышает, то РД принимается, как дополнение до 360°, при этом меняется знак.
Если судно шло на восток, РД имеет знак +, если на запад – знак –.
Истинный курс, истинный пеленг, курсовой угол
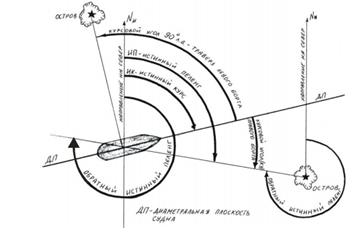
Истинный пеленг– двугранный угол между северной частью плоскости истинного меридиана и направлением на пеленгуемый предмет.
Обратный истинный пеленг– угол, отличающийся от истинного пеленга на 180°
«+»— если ОИП 180°.
Курсовой угол – двугранный угол между носовой частью диаметральной плоскости лодки и направлением на предмет.
Курсовой угол правого борта +, левого борта –.
4. Земной магнетизм, магнитное склонение, девиация.
Магнитные полюса отличаются от географических.
Если МП отклонен к востоку от ГП – знак +
Если МП отклонен к западу от ГП – знак –
d = 2,4° W 2006г Год. изм. 0,14° к E: магнитное склонение 2,4° к западу, измерено в 2006 году, годовое изменение 0,14° к востоку.
Магнитный угол – угол в плоскости истинного горизонта между северной частью магнитного меридиана и диаметральной плоскостью судна.
Магнитный пеленг – угол в плоскости истинного горизонта между северной частью магнитного меридиана и направлением на предмет.
Измеряется в круговой системе отсчета от 0 до 360°
Девиация δ – отклонение стрелки магнитного компаса от магнитного меридиана под действием магнитного поля судна (угол между магнитным и компасным меридианами).
Измеряется для каждого судна на углах 0, 45, 90, 135, 180, 225, 270, 315°
Компасный пеленг – угол в плоскости истинного горизонта между северной частью магнитного меридиана и направлением на предмет.
Истинный курс
d + δ = Δ – поправка МК.
Δ измеряется в полукруговой системе и имеет свой знак.
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
НАВИГАЦИЯ. ГЛАВА 1. §§2-3. Географическая система координат. Разность широт и разность долгот
§ 2. Географическая система координат
Для определения положения точек на земной поверхности могут применяться различные системы координат: географическая, прямоугольная, полярная и др. Наиболее употребительной является система географических координат.
Малая ось эллипсоида пересекает поверхность последнего в двух точках, которые называются северными и южным полюсами. Плоскости, проходящие через ось вращения Земли, называются плоскостями земных меридианов, которые в сечении с поверхностью Земли образуют большие круги, называемые меридианами.
Плоскость, перпендикулярная земной оси и проходящая через центр эллипсоида, называется плоскостью экватора. Большой круг, образующийся от пересечения этой плоскости с поверхностью эллипсоида, называется земным экватором. Плоскости, параллельные плоскости земного экватора в сечении с поверхностью Земли, образуют малые круги, называемые земными параллелями.
Координатными осями системы географических координат приняты: экватор и один из меридианов, принимаемый за начальный; координатными линиями являются земные параллели и меридианы, а величинами, определяющими положение точек, т. е. координатами, географическая широта и географическая долгота.
Широта
Географической широтой точки на поверхности Земли называется угол между нормалью поверхности эллипсоида в этой точке и плоскостью экватора.
(на рис. 3 для точки М угол МОС)
Если принять форму Земли за шар, то будет верным такое определение широты:
Географическая широта в кораблевождении обозначается греческой буквой φ (фи).
Широта отсчитывается от экватора к полюсам от 0 до 90° и измеряется дугой меридиана от экватора до параллели данной точки.
Широты северного полушария обозначаются буквой N, и считаются положительными. При аналитических расчетах они принимаются со знаком плюс «+».
Широты точек южного полушария, обозначаемые буквой S, считаются отрицательными и им приписывается знак минус «-».
Географическая широта определяет положение параллели, на которой находится определяемая точка.
Долгота
Двугранный угол измеряется сферическим углом при полюсе между начальным меридианом и меридианом определяемой точки или численно равной ему дугой экватора, заключенной между названными меридианами (на рис. 3 для точки М угол АОС).
Соответственно, можно сказать, что:
Географическая долгота измеряется меньшей из дуг экватора между начальным меридианом и меридианом точки.
За начальный меридиан в принципе может приниматься любой земной меридиан. По международному соглашению 1884 г. большинством стран мира за начальный принят меридиан, проходящий через Гринвичскую обсерваторию, расположенную около Лондона.
Счет географических долгот ведется к востоку и западу от Гринвичского меридиана от 0 до 180°.
Географическая долгота в кораблевождении обозначается греческой буквой λ (лямбда).
Долготы точек, находящихся в восточном полушарии, принято считать положительными (знак плюс), западные долготы считаются отрицательными (знак минус). При определении долготы той или иной точки земной поверхности обязательно указывают на ее наименование:
/ Ниже следующая информация этого параграфа к прочтению не обязательна, но интересна и, должно быть, необходима шкиперам, планирующим дальние путешествия./👇🤕
В зависимости от метода вычисления географических координат различают координаты геодезические и астрономические.
В геометрическом определении геодезических координат никакой разницы с общей формулировкой географических координат нет. Места точек, фиксируемых геодезической широтой и геодезической долготой, относятся к математически правильной фигуре—эллипсоиду вращения.
А вот при определении места астрономическими способами наблюдатель имеет дело с линией отвеса, совпадающей с направлением силы тяжести, а не с нормалью к поверхности эллипсоида.
Поэтому в астрономической системе координат
Широта определится как угол между плоскостью экватора и направлением отвеса в данной точке.
Долгота места, определенного астрономическим способом, представляет собой двугранный угол между плоскостью начального меридиана (Гринвичского) и плоскостью астрономического меридиана данной точки.
Астрономический меридиан — это след от сечения земной поверхности плоскостью, проходящей через отвесную линию в данной точке и параллельной оси мира.
Из определения астрономических координат видно, что они в отличие от геодезических координат фиксируют положение точек относительно поверхности действительной фигуры Земли —геоида.
Нормаль к поверхности земного эллипсоида в общем случае не проходит через центр Земли. Вместе с тем при решении астрономических задач, а также ряда специальных задач математической картографии появляется необходимость определять положение точек земной поверхности относительно центра Земли. В этом случае долгота произвольной точки К определится также, как и в географической системе координат, а широта получится как угол между плоскостью экватора и прямой, соединяющей данную точку с центром эллипсоида.Такая широта называется геоцентрической широтой и обозначается φ’
На рисунке №6 видно, что геоцентрическая широта в общем случае меньше географической широты на величину редукции r широты, которая может быть подсчитана по формуле
Для точек, расположенных на экваторе и на полюсе, редукция широты равна нулю. Наибольшего значения (11,5′) редукция достигает в широте 45°.
§ 3. Разность широт и разность долгот
Географические координаты — широта и долгота — однозначно определяют положение конкретной точки земной поверхности.
Переход от одной точки земной поверхности к другой сопровождается изменением их географических координат.
Точки, лежащие на одной параллели, имеют одинаковую широту и разные долготы.
Точки, расположенные на одном меридиане, имеют одну и ту же долготу и различные широты.
В общем случае две точки, не находящиеся на одном меридиане или на одной параллели, имеют разные широты и разные долготы.
В практике кораблевождения часто необходимо знать, как изменились или изменятся географические координаты при переходе из одной точки земной поверхности в другую, и уметь вычислять эти изменения. Величинами, характеризующими изменение географических координат при переходе от одной точки земной поверхности к другой, являются разность широт и разность долгот.
Разностью широт (РШ) двух точек на поверхности Земли называется дуга меридиана, заключенная между параллелями этих точек.
Для вычисления разности широт пользуются формулой
Действительно, на рисунке №7 видно, что изменение широты (РШ) при переходе корабля из точки А в точку Б характеризуется дугой А’Б, численно равной разности дуг меридианов точек прихода Б и отхода А, определяемых соответственно широтами φБ и φА.
Рассчитанной по формуле разности широт приписывается знак плюс, если она совершена к N, и знак минус, если разность широт совершена к S.
Разность широт может изменяться от 0 до ±180°.
Разность долгот (РД), характеризующая изменение долготы, как видно из рисунка, представляет собой центральный угол между меридианами двух точек.
Этот угол измеряется дугой экватора между указанными меридианами. На этом основании
Разностью долгот двух точек на поверхности Земли называется меньшая из дуг экватора, заключенная между меридианами этих точек.
Из этого определения следует, что разность долгот может иметь значения от 0 до ±180°.
С учетом ранее принятых обозначений (для восточной долготы знак плюс и для западной — минус) можно написать формулу для вычисления РД двух точек:
Разность долгот будет иметь знак плюс, если она совершена к Е, и знак минус, если она совершена к W.
Указанное правило имеет следующий геометрический смысл: если меридиан пункта прихода λ 2 располагается восточнее меридиана пункта отхода λ 1, значит, разность долгот сделана к Е и ей приписывается знак плюс. И наоборот, когда меридиан пункта прихода расположен западнее меридиана пункта отхода, разность долгот сделана к W и ей приписывается знак минус.
При решении задачи на расчет РД по формуле может получиться результат, превышающий 180°. В этих случаях для нахождения меньшей из дуг экватора полученный результат следует вычесть из 360° и изменить знак (наименование) его на обратный.
Найти РД двух точек с долготами λ2 = 164°15’Е и λ1 = 147°28’W.
Находим дополнение до 360° и меняем знак:
РД = — 48°17′ = 48°17’к W.
Вычисления РШ и РД по приведенным формулам рекомендуется сопровождать построением чертежа, что, кроме контроля правильности решения, развивает пространственное воображение.
§ 4. Понятие о радиусах кривизны главных сечений в данной точке земного эллипсоида
Я опускаю, так как не желаю Вам той же головной боли, что была испытана мною при его изучении.