что такое размерность векторного пространства
Векторное пространство: база и размерность, аксиомы, свойства
Содержание:
А векторное пространство непустое множествоV=<или, v, ш, ……>, элементами которого являются векторы. С ними проводят некоторые важные операции, среди которых выделяются следующие:
— Сумма между двумя векторами u + v какие результаты z, который принадлежит множеству V.
— Умножение действительного числа α на вектор v: α v что дает другой вектор Y который принадлежит V.
Аксиомы и свойства
Чтобы векторное пространство было задано, должны быть выполнены следующие восемь аксиом:
1-переключаемый: или +v = v +или
2-транзитивность: (или + v) + ш = или + ( v + ш)
3-Существование нулевого вектора 0 такой, что 0 + v = v
5-Дистрибутивность произведения по векторной сумме: α ( или + v ) = αили +αv
6-Дистрибутивность произведения относительно скалярной суммы: (α + β)v = αv +βv
7-ассоциативность скалярного произведения: α (β v) = (α β)v
8-число 1 является нейтральным элементом, поскольку: 1v = v
Примеры векторных пространств
Пример 1
Сумму двух векторов на плоскости можно определить как операцию геометрического переноса второго вектора после первого. Результатом суммы является ориентированный сегмент, который начинается от начала первого и достигает вершины второго.
На рисунке видно, что сумма в R² коммутативна.
Мы также определяем произведение числа α и вектора. Если число положительное, направление исходного вектора сохраняется, а размер в α раз больше исходного вектора. Если число отрицательное, направление противоположное, и размер результирующего вектора является абсолютным значением числа.
Вектор напротив любого вектора v это –v =(-1) v.
Все сказанное проиллюстрировано на рисунке 2.
Пример 2
Задавать п всех многочленов степени меньше или равной двум, включая нулевую степень, образуют набор, который удовлетворяет всем аксиомам векторного пространства.
Пусть многочлен P (x) = a x² + b x + c и Q (x) = d x² + e x + f
Определяется сумма двух многочленов: P (x) + Q (x) = (a + d) x² + (b + e) x + (c + f)
Сумма многочленов, принадлежащих множеству п он коммутативен и транзитивен.
Нулевой многочлен, принадлежащий множеству п тот, у которого все коэффициенты равны нулю:
Сумма скаляра α по многочлену определяется как: α P (x) = α ∙ a x² + α ∙ b x + α ∙ c
Из всего вышесказанного следует, что множество п всех многочленов степени меньше или равной двум, это векторное пространство.
Пример 3
Задавать M всех матриц из m строк x n столбцов, элементы которых являются действительными числами, образуют вещественное векторное пространство относительно операций сложения матриц и произведения числа на матрицу.
Пример 4
Множество F непрерывных функций действительной переменной образуют векторное пространство, поскольку можно определить сумму двух функций, умножение скаляра на функцию, нулевую функцию и симметричную функцию. Они также выполняют аксиомы, характеризующие векторное пространство.
База и размерность векторного пространства
Основание
Базис векторного пространства определяется как набор линейно независимых векторов, так что любой вектор этого векторного пространства может быть сгенерирован из их линейной комбинации.
Линейное объединение двух или более векторов состоит из умножения векторов на некоторый скаляр и последующего векторного сложения.
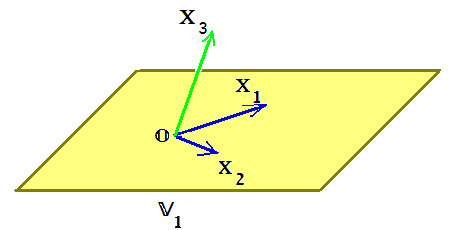
Например, в векторном пространстве векторов в трех измерениях, образованном R³, используется канонический базис, определяемый единичными векторами (с величиной 1). я, j, k.
куда я = ( 1, 0, 0 ); j = ( 0, 1, 0 ); k = (0, 0, 1). Это декартовы или канонические векторы.
Любой вектор V принадлежащий R³, записывается как V = а я + b j + c k, который представляет собой линейную комбинацию базовых векторов я, j, k. Скаляры или числа a, b, c известны как декартовы компоненты V.
Также сказано, что базовые векторы векторного пространства образуют генераторную установку векторного пространства.
Размер
Основания векторного пространства не уникальны, но все основания одного векторного пространства имеют одинаковую размерность.
Векторное подпространство
Примером векторного подпространства являются векторы, принадлежащие плоскости XY. Это подпространство является подмножеством векторного пространства размерности больше, чем набор векторов, принадлежащих трехмерному пространству XYZ.
Другой пример векторного подпространства S1 векторного пространства S, образованного всеми матрицами 2 × 2 с действительными элементами, определяется ниже:
С другой стороны, S2, определенный ниже, хотя и является подмножеством S, не образует векторное подпространство:
Решенные упражнения
-Упражнение 1
Пусть векторы равны V1=(1, 1, 0); V2= (0, 2, 1) и V3= (0, 0, 3) в R³.
а) Покажите, что они линейно независимы.
б) Покажите, что они образуют базис в R³, поскольку любую тройку (x, y, z) можно записать как линейную комбинацию V1, V2, V3.
в) Найдите компоненты тройки V= (-3,5,4) у основания V1, V2, V3.
Решение
Критерий демонстрации линейной независимости состоит в установлении следующей системы уравнений относительно α, β и γ
α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3) = (0, 0, 0)
Чтобы получить значения α, β и γ, мы предлагаем следующую систему уравнений:
Ответ на
Сделан вывод, что это набор линейно независимых векторов в R³.
Ответ б
Теперь давайте запишем тройку (x, y, z) как линейную комбинацию V1, V2, V3.
(x, y, z) = α V1 + β V2 + γ V3 = α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3)
α ∙ 1 + β ∙ 0 + γ ∙ 0 = x
α ∙ 1 + β ∙ 2 + γ ∙ 0 = y
α ∙ 0 + β ∙ 1 + γ ∙ 3 = z
Первый указывает α = x, второй β = (y-x) / 2 и третий γ = (z- y / 2 + x / 2) / 3. Таким образом, мы нашли образующие α, β и γ любой тройки R³
Ответ c
Перейдем к поиску составляющих тройного V= (-3,5,4) у основания V1, V2, V3.
Подставляем соответствующие значения в выражения для генераторов, найденные выше.
Мы делаем вывод, что V1, V2, V3 образуют базис в векторном пространстве R³ размерности 3.
-Упражнение 2.
Решение
P (t) = x P1 (t) + y P2 (t) + z P3 (t)
где числа x, y, z подлежат определению.
Умножая и группируя члены с одинаковой степенью по t, получаем:
Это приводит нас к следующей системе уравнений:
Решениями этой системы уравнений являются:
-Упражнение 3.
Решение
Мы линейно объединяем три вектора v1, v2, v3 и мы требуем, чтобы комбинация добавляла нулевой элемент R⁴
к v1 + b v2 + c v3 = 0
Это приводит нас к следующей системе уравнений:
Если мы подставим этот результат в первое уравнение, мы придем к выводу, что b = 0.
Наконец, a = b = c = 0, так что можно сделать вывод, что векторы v1, v2 и v3 линейно независимы.
Ссылки
В каком веке началась независимая жизнь Мексики?
Технонаука: характеристики, применение, этические последствия
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Благодарю Ю.А.Смолькина за обнаружение 07.08.19 ошибки на настоящей странице и информирование о ней.
Линейное пространство
Определения
Примеры линейных пространств
Почему множество решений системы неоднородных уравнений не образует линейного подпространства?
В пространстве квадратных матриц фиксированного порядка каждое из следующих подмножеств составляет линейное подпространство: симметричных, кососимметричных, верхнетреугольных, нижнетреугольных и диагональных матриц.
Изоморфизм
Линейная зависимость, базис, координаты
Пример. Для полиномов нескольких переменных свойство линейной зависимости является частным проявлением более общего свойства функциональной зависимости. Так, однородные полиномы (формы)
Теорема 2. а) Если система содержит хотя бы один нулевой вектор, то она л.з.
б) Если система л.н.з., то и любая ее подсистема л.н.з.
Две системы векторов называются эквивалентными если каждый вектор одной системы линейно выражается через векторы другой и обратно.
Теорема 4. Системы векторов
Теорема 5. Если каждая из двух эквивалентных систем
Пример [1]. Замечательный пример трехмерного линейного пространства дает нам совокупность всех цветов. Под суммой двух цветов будем понимать цвет, образованный их смешением
Анимация ☞ ЗДЕСЬ (1500 K, gif)
Пример. Найти базис подпространства
Ответ. Базис составляют, например, первая, вторая и четвертая строки.
Найти координаты полинома
Критерии линейной зависимости
Относительный базис
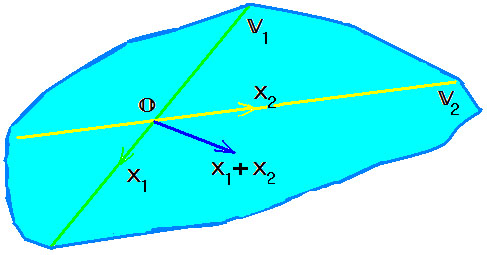
Сумма и пересечение линейных подпространств
Понятие пересечения линейных подпространств совпадает с понятием пересечения их как множеств.
Теорема. Имеет место формула:
Доказательство ☞ ЗДЕСЬ.
Можно ли обобщить этот результат на случай трех (и более подпространств)? Cправедлив ли, к примеру, аналог формулы включений-исключений в следующем виде:
Теорема. Имеет место формула:
Пример. Найти базис суммы и размерность пересечения
Найти базисы суммы и пересечения подпространств
Решение ☞ ЗДЕСЬ.
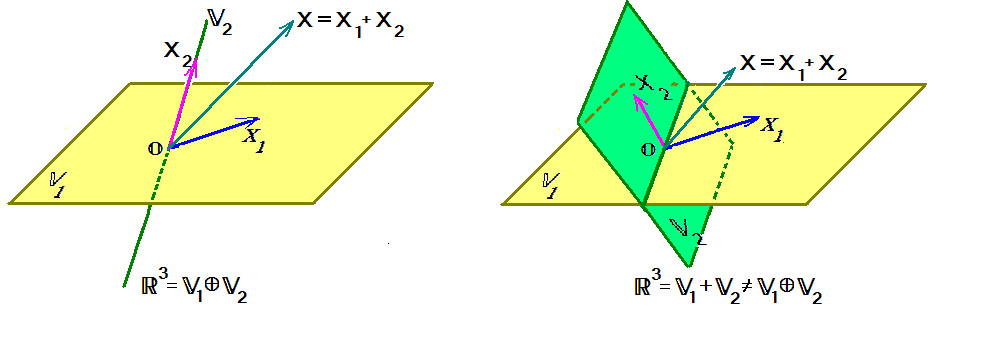
Прямая сумма линейных подпространств
Пример [2]. Доказать, что сумма подпространств
Линейные многообразия
Некоторые задачи на линейные многообразия ☞ ЗДЕСЬ.
Векторное пространство
Полезное
Смотреть что такое «Векторное пространство» в других словарях:
векторное пространство — — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=5045] векторное пространство линейное пространство Множество векторов с одинаковым числом компонент, важнейшее для математической экономики понятие. Компонентами векторов… … Справочник технического переводчика
Векторное пространство — У этого термина существуют и другие значения, см. Пространство. Векторное (линейное) пространство основной объект изучения линейной алгебры. Содержание 1 Определение 2 Простейшие свойства … Википедия
векторное пространство — vektorių erdvė statusas T sritis radioelektronika atitikmenys: angl. vector space vok. Vektorraum, m rus. векторное пространство, n; пространство векторов, n pranc. espace vectoriel, m … Radioelektronikos terminų žodynas
векторное пространство — математическое понятие, обобщающее понятие совокупности всех векторов 3 мерного пространства на случай произвольного числа измерений. * * * ВЕКТОРНОЕ ПРОСТРАНСТВО ВЕКТОРНОЕ ПРОСТРАНСТВО, математическое понятие, обобщающее понятие совокупности… … Энциклопедический словарь
векторное пространство — vektorinė erdvė statusas T sritis fizika atitikmenys: angl. vector space vok. Vektorraum, m rus. векторное пространство, n pranc. espace vectoriel, m … Fizikos terminų žodynas
ВЕКТОРНОЕ ПРОСТРАНСТВО — линейное пространство, над полем К, аддитивно записанная абелева группа Е, в которой определено умножение элементов на скаляры, т. е. отображение удовлетворяющее следующим аксиомам Из аксиом 1) 4) вытекают следующие важные свойства векторного… … Математическая энциклопедия
ВЕКТОРНОЕ ПРОСТРАНСТВО — матем. понятие, обобщающее понятие совокупности всех векторов 3 мерного пространства на случай произвольного числа измерений … Большой энциклопедический политехнический словарь
ВЕКТОРНОЕ ПРОСТРАНСТВО — (линейное про странство) (матем.), обобщающее понятие совокупности всех векторов 3 мерного пространства … Естествознание. Энциклопедический словарь
ТОПОЛОГИЧЕСКОЕ ВЕКТОРНОЕ ПРОСТРАНСТВО — над топологическим полем (т. п.), К векторное пространство Енад К, наделенное топологией, согласующейся со структурой векторного пространства, т. е. удовлетворяющей следующим аксиомам: 1) отображение непрерывно; 2) отображение непрерывно (при… … Математическая энциклопедия
Нормированное векторное пространство — У этого термина существуют и другие значения, см. Пространство. В нашем пространстве понятие «длина вектора» понимается интуитивно как расстояние между его началом и концом. Наиболее важными свойствами «длины вектора» являются следующие: Длина… … Википедия