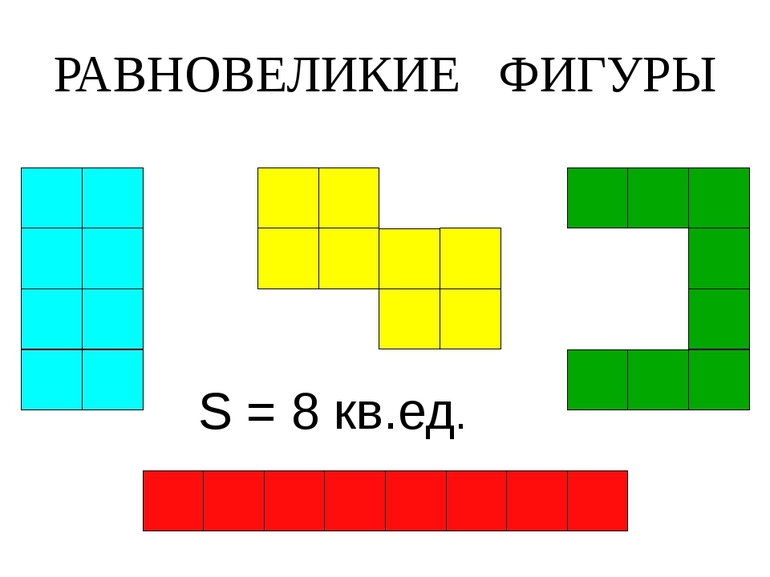
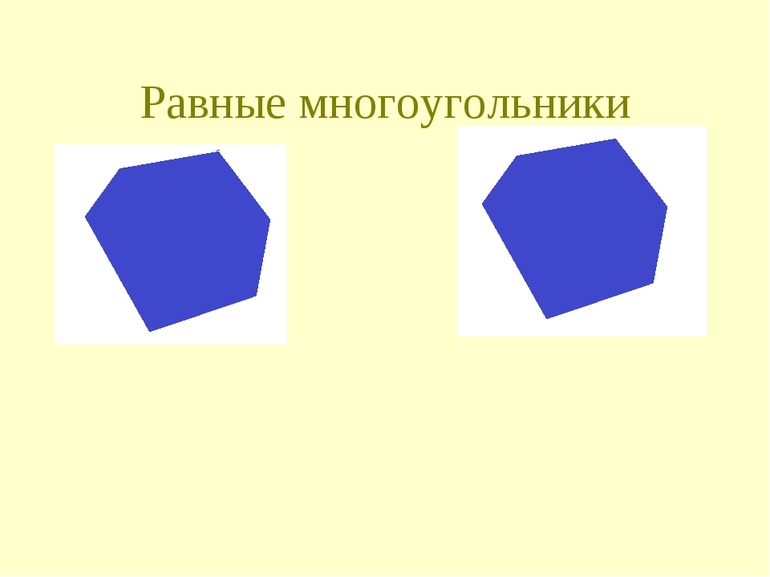
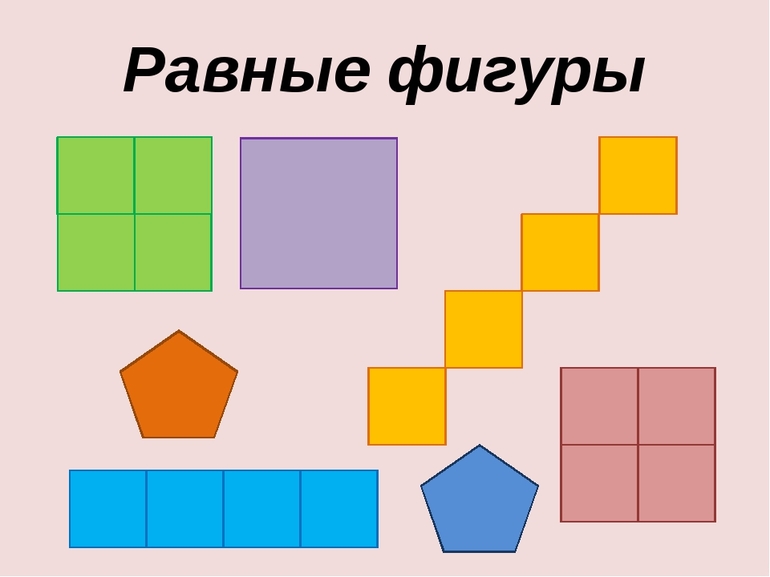
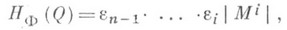что такое равновеликие многоугольники

Равные многоугольники

По определению равные фигуры должны быть во всём одинаковыми, включая площадь, длину сторон, размер углов и другие параметры. Чтобы рассмотреть всё из них, уйдёт много времени, да это и не нужно, ведь они взаимозависимы. Хорошим примером будет самый простой многоугольник — треугольник. Существует несколько правил, по которым можно определить, равны ли 2 треугольника между собой или нет:

Нельзя путать первое условие с тремя углами. Ведь если в треугольнике равны 3 угла, они необязательно будут равными, но будут подобными.

Названия условий достаточно точно описывают критерии, по которым можно определить одинаковые 2 треугольника или нет. Из них следует, что необязательно знать все параметры: часто хватает только нескольких из них для определения «равности».

В большинстве случаев определить одинаковость других фигур гораздо сложнее, нежели треугольников. К счастью, чаще всего в школьной геометрии такой класс задач не рассматривают или даются дополнительные данные, помогающие с решением.

Например, доказательство «равности» для четырёхугольника сложнее, да и почти не встречается. Но если по условию сказано, что четырёхугольник не произвольный, а имеет прямые углы, задача становится проще. В таком случае рассматривается прямоугольник. А для него достаточно, чтобы 2 не противолежащие стороны были равны.

Если указано ещё и условие, что прямоугольник является квадратом, достаточно указать, что у двух таких фигур совпадает по длине одна сторона и уже этого будет достаточно.

Равность правильных фигур

Частным и самым простым для сравнения является случай, когда многоугольник по условию правильный. Так называется фигура с одинаковыми сторонами и углами. Например, равносторонний треугольник и квадрат. Важно не забывать проверить равны ли углы, так как не каждая фигура правильная. Тот же ромб по определению имеет 4 совпадающие по длине стороны, но разные углы. При сравнении правильных многоугольников достаточно указать, что, хотя бы одна сторона фигуры равна стороне у другой. Это будет достаточное условие для доказательства «равности».

Самым простым и наглядным способом сверки двух фигур будет не геометрический с помощью правил, а путём наложения рисунков друг на друга. Разумеется, что он не претендует на точность, но изобразить параллелограмм и наложить его на другой нагляднее, чем сравнивать, например, углы. Понятно, что так можно только ознакомиться с концепцией «равности» и показать, какие фигуры называются равными, для упрощения в дальнейшем решения задач, но доказывать что-либо нельзя, ввиду неточности метода.

Если при сравнении двух тел оказывается, что их площади равны, такие тела (многоугольники) являются равновеликими. Как и в случае с прошлым, это определение звучит несложно. Проблемы могут начаться непосредственно при вычислении площадей. Самый простой многоугольник — треугольник. Для вычисления его площади существует множество способов.

Вычисление площади треугольника

Чаще всего приходится работать с прямоугольными треугольниками. Их площадь вычислить несложно — это полупроизведение катетов (сторон, между которыми лежит прямой угол). Таким образом, даже если стороны двух фигур по длине разные, но их произведение равно, они равновеликие. Например, треугольник с катетами 4 и 4 равен по площади многоугольнику с катетами 16 и 1. Так как их полупроизведение, а значит и площадь равна 8.

Если же треугольник произвольный (то есть не является частным случаем — прямоугольным, равнобедренным или равносторонним), можно воспользоваться одной из 5 формул, позволяющих вычислить его площадь.

То, какую формулу использовать, будет зависеть от данных, предоставленных в задаче. Иногда придётся проводить дополнительное построение, например, провести высоту или использовать свойства, что биссектрисы пересекаются в центре вписанной окружности. Если не даны все 3 стороны, использовать третью формулу не получится.

Важно понять, что фигуры могут быть разными по количеству углов, но всё равно считаться равновеликими — в учёт идёт только площадь, остальные параметры не важны. Например, прямоугольный треугольник с катетами 2 и 4 будет визуально казаться больше, чем квадрат со стороной 2, но их площади совпадают и равны 4 (площадь прямоугольника считается как произведение прилежащих сторон друг на друга). По определению это делает их равновеликими.

Визуальный способ

Существует также наглядный, но неточный способ. Нужно взять листок в клеточку и нарисовать на нём многоугольники. Если рисунок получился большой — не страшно, так будет только проще в дальнейшем. Следующий шаг — посчитать количество клеток, которое заняла каждая фигура и сравнить. Если оно равно, равновеликость доказана. Опять же метод не точный, но для введения в концепцию площадей и их «равности» подойдёт.

Иногда встречается словосочетание «равносоставленная фигура». Такими называют произвольные многоугольники, которые можно составить друг из друга путём разрезания одного из них на одинаковые объекты и перекладывания. Например, если прямоугольник 4 на 1 нарезать на одинаковые части — квадраты 1 на 1, то из полученных маленьких квадратов можно составить один большой со стороной 2. Но это не более чем забавное свойство некоторых фигур и в геометрии фактически почти не используется.

Источник

РАВНОВЕЛИКИЕ И РАВНОСОСТАВЛЕННЫЕ ФИГУРЫ

Для 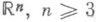, равновеликость означает равенство объемов; равносоставленность многогранников определяется аналогично с . Эти понятия обобщаются также на неевклидовы геометрии.

Площадь (многоугольника) есть функция s(M), удовлетворяющая следующим аксиомам:

(a) 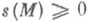для любого многоугольника М;

(d) площадь квадрата, стороной которого является единица длины, равна 1.

С помощью этих аксиом определяется площадь прямоугольника.

Теорема. Если два многоугольника равносостав-лены, то они равновелики.

На этой теореме основан метод разбиения, известный еще Евклиду: для вычисления площади многоугольника пытаются разбить его на конечное число частей, из к-рых можно составить фигуру известной площади. Напр., параллелограмм равносоставлен с прямоугольником, имеющим то же основание и ту же высоту (см. рис. 1); треугольник равносоставлен с параллелограммом, имеющим то же основание и вдвое меньшую высоту (см. рис. 2).

Таким образом, вся теория площадей многоугольников может быть построена на основе теоремы о площади прямоугольника.

Существует и другой способ вычисления площадей, основанный на аксиомах (b) и (g),- метод дополнения. Два многоугольника наз. равнодополняемыми, если их можно дополнить соответственно конгруэнтными частями так, чтобы получились конгруэнтные многоугольники.

Напр., параллелограмм и прямоугольник с одинаковыми основаниями и одинаковыми высотами равнодополняемы (см. рис. 3) и потому равновелики.

В евклидовой плоскости два многоугольника в том и только в том случае равновелики, если они равносоставлены (а также если они равнодополняемы). Аналогичная теорема справедлива в плоскости Лобачевского и в эллиптической плоскости. Напротив, в неархимедовой геометрии эквивалентны лишь равновеликость и равнодополняемость; равновеликость же им не эквивалентна.

Два равновеликих многогранника в том и только в том случае Г-равносоставлены, если для каждого флангового инварианта Н ф его значения на этих многогранниках одинаковы.

Многогранник в том и только в том случае, если Н ф ( М п )=0 для всех флаговых инвариантов H Ф порядков, меньших k.

Пусть при гомотетии с коэффициентом l>0 объем n-мерного многогранника увеличивается в l n раз. Если принять это утверждение как аксиому, то объем любого многогранника может быть найден методом разбиения.

Лит.:[1] Проблемы Гильберта, М., 1969; [2] Болтянский В. Г., Равновеликие и равносоставленные фигуры, М., 1956; [3] его же, Третья проблема Гильберта, М., 1977; [4] Xадвигер Г., Лекции об объеме, площади поверхности и изопериметрии, пер. с нем., 1966; [5] Iessen В., Тhorup A., «Math. Scand.», 1978, v. 43, fasc. 2, p. 211-40.

Источник

Математика

Развитие соображений о равенстве площадей представляет собою ценный материал для приучения учащихся к обобщающей работе мысли, а потому оно никоим образом не должно комкаться так, как это обычно имеет место в наших ходовых учебниках.

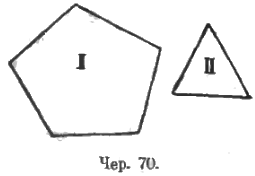
Прежде всего тот процесс наложения, который неоднократно имел место в предыдущем, позволит учащимся установить, что две площади следует считать равными, если они при наложении совпадают. Далее ставим на очередь вопрос о сложении двух площадей (напр., I и II), ограниченных прямыми линиями (чер. 70). В основе сложения лежит, как мы уже знаем, процесс сдвижения, а здесь мы можем две наших площади (I и II) сдвинуть множеством различных способов. Следует, чтобы учащиеся выполнили (при помощи циркуля и линейки), по крайней мере, два различных построения нахождения суммы I и II площадей, которые в результате давали бы 2 площади, не совпадающие между собою при наложении. Учащиеся уже знают переместительный закон сложения для чисел, для отрезков, для углов – теперь становится необходимым обобщить этот переместительный закон и принять, что, как бы мы ни придвинули одну площадь к другой, результаты этих сдвижений должны считаться равными. Обратив хотя некоторое внимание на сложение трех и более площадей (а, следовательно, и на обобщение свойства сложения, что при сложении многих слагаемых их можно складывать любыми группами и в любом порядке, – а это свойство является следствием переместительного и сочетательного законов), мы приходим к установлению второго признака равенства площадей: две площади (ограниченные прямыми) должны считаться равными, если каждая из них является суммою площадей, попарно совпадающих при наложении (здесь, в сущности, имеется еще одно обстоятельство: каждая площадь должна считаться суммою конечного числа слагаемых).

Переходим к вычитанию площадей. Опять видим (применяясь, напр., к I и II площадям), что это вычитание можно выполнить разнообразными способами, что влечет за собою новый признак равенства площадей: две площади должны считаться равными, если каждая из них есть разность площадей, совпадающих при наложении.

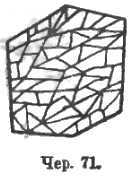
Как известно, наука устанавливает 3 разных термина для этих трех случаев равенства площадей: 1) равенство по наложению – конгруэнтные площади, 2) равенство по сложению – равносоставленные площади и 3) равенство по вычитанию – равновеликие площади. Здесь возникают тонкие вопросы, и, быть может, должно об них побеседовать с учащимися: 1) не могут ли две равносоставленные площади быть не равными по наложению, т. е. пусть некоторая площадь разбита на много (но не на бесконечно большое число) слагаемых (чер. 71), – нельзя ли эти слагаемые площади переложить так, чтобы из них получилась новая площадь, явно не совмещающаяся с начальной, напр., чтобы вся новая площадь умещалась внутри начальной или, наоборот, чтобы новая площадь закрывала всю начальную, да еще захватывала бы какой-либо кусок плоскости, лежащий вне начальной? 2) Обязательно ли две равновеликие площади в то же время и равносоставлены? Другими словами: две площади, равные по вычитанию, должны ли быть равными и по сложению? Смысл этих вопросов сводится, конечно, к общему вопросу: не может ли оказаться противоречий при применении трех вышеустановленных признаков равенства площадей? Эти вопросы послужили предметом научных изысканий (принцип Де-Цольта, теория площадей Гильберта), но знакомить учащихся с этими изысканиями не представляется возможным, и приходится ограничиваться лишь тем, что эти вопросы не должны замалчиваться перед учащимися. Последние, на основе своих непосредственных представлений, приходят к установлению отсутствия противоречий в трех вышеуказанных признаках равенства площадей и, следовательно, к заключению:

Две площади равны: 1) если они совпадают при наложении и 2) если каждая из них является суммою или разностью площадей, совпадающих попарно при наложении.

Установленные признаки для применения к площадям понятий «больше» или «меньше» не представляет трудности.

Основные проекты учения о равновеликости многоугольников (два многоугольника называют равновеликими, если равны их площади) таковы: 1) равновеликость двух параллелограммов с равными основаниями и высотами (следует указать на возможность видеть, что площади таких параллелограммов равны и по вычитанию и по сложению); 2) равновеликость треугольников, имеющих равные основания и равные высоты; 3) превращение треугольника в равновеликий прямоугольник, четыреугольника – в треугольник, пятиугольника (и т. д.) – также в треугольник; 4) теорема Пифагора.

Лучшим способом выяснения теоремы Пифагора считаю, согласно свой практике, следующий.

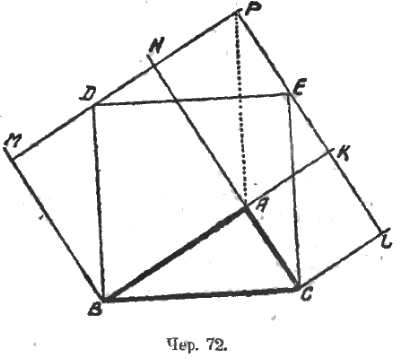
Предлагаем учащимся выполнить следующее (сложное) построение. Строим (чер. 72):

1) прямоугольный треугольник BAC (∠A = d).

2) Квадрат BDEC на гипотенузе BC (BD ⊥ BC, CE ⊥ BC, BD = EC = BC).

3) AK – продолжение BA, CL || AK и прямую EL (через точку E) || AC – получится квадрат CAKL на катете AC (для выяснения этого придется рассмотреть ∆ECL и ∆BAC; у них BC = EC и ∠BCA = ∠ECL; так как эти треугольника прямоугольные, то этого достаточно, чтобы быть убежденным в их равенстве, т. е. ∆ECL = ∆BAC).

4) AN – продолжение CA, BM || AN и прямую MDN (через точку D) || BA – получим квадрат BMNA на катете BA (выясняется это при помощи равенства треугольников BMD и BAC).

5) NP – продолжение MN и KP – продолжение LK; наконец, – прямую PA.

Тогда получим еще 3 треугольника, равных начальному, а именно: ∆DPE, ∆ANP и ∆PKA.

Итак, имеем: ∆ABC = ∆CEL = ∆BDM = ∆DPE = ∆ANP = ∆PKA.

Мы видим, что придется от всей застроенной площади BMPLCB отрезать 3 куска, а именно: площади треугольников BMD, DPE и CEL, чтобы получить площадь квадрата BDEC. Но у нас имеется 6 равных треугольников; если от застроенной площади BMPLCB отрезать площади остальных трех треугольников (т. е. ∆BAC, ∆ANP и ∆PKA), то получим площади двух квадратов ABMN и AKLC, откуда и приходим к выводу, что площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.

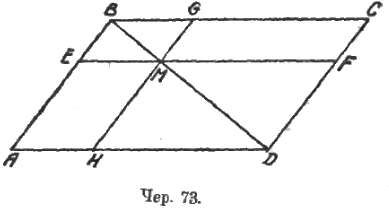
Очень хорошо ввести в дело и знаменитое евклидово построение (чер. 73), дающее возможность получить 2 равновеликих параллелограмма, имеющих и разные стороны и разные высоты, но равные углы. Это построение таково. Строим: 1) параллелограмм ABCD, 2) его диагональ BD, 3) через любую точку M его диагональ BD две прямые: EF || BC и GH || BA.

Тогда легко видеть:

1) площадь AEMH = площади MGCF и

2) площадь ABGH = площади EBCF.

Это построение можно применить к решению ряда вопросов и задач (см. приложение), а с учащимися его следует использовать для превращения данного прямоугольника в другой, равновеликий ему и имеющий данное основание. Это важно потому, что таким образом видно, что для решения этой задачи не надо ни умения измерять площади, ни знания пропорциональности отрезков (при обычном решении этой задачи всем этим пользуются).

Источник

Равновеликие фигуры

Пло́щадь фигуры — числовая характеристика фигуры. В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов.

Содержание

Об определении

Формальное введение понятия площадь и объём можно найти в статье мера Жордана, здесь мы приводим лишь намётки определения с комментариями.

Площадь — это вещественнозначная функция, определённая на определённом классе фигур евклидовой плоскости, такая что:

Определённый класс должен быть замкнут относительно пересечения и объединения, а также относительно движений плоскости и включать в себя все многоугольники. Из этих аксиом следует монотонность площади, то есть

Связанные определения

Комментарии

На самом деле, есть довольно неестественный и неоднозначный способ определить площадь для всех ограниченных подмножеств плоскости. На множестве всех ограниченных подмножеств плоскости существуют различные функции площади, т. е. не равные функции, удовлетворяющие вышеприведённым аксиомам, а множество квадрируемых фигур является максимальным множеством фигур на которых функционал площади определяется однозначно.

То же самое можно сделать для длины на прямой, но нельзя для объёма в евклидовом пространстве и также нельзя для площади на единичной сфере в евклидовом пространстве, (смотри соответственно парадокс Банаха — Тарского и парадокс Хаусдорфа).

Площади некоторых фигур

Площадь прямоугольника со сторонами а и b равна произведению их сторон: S = ab.

Площадь произвольного четырехугольника равна половине произведения диагоналей и синуса угла между ними.

Площадь треугольника равна половине произведения основания, умноженного на высоту.

См. также

Ссылки

Полезное

Смотреть что такое «Равновеликие фигуры» в других словарях:

РАВНОВЕЛИКИЕ ФИГУРЫ — плоские фигуры с одинаковыми площадями или геометрические тела с одинаковыми объемами … Большой Энциклопедический словарь

равновеликие фигуры — плоские фигуры с одинаковыми площадями или геометрического тела с одинаковыми объёмами. * * * РАВНОВЕЛИКИЕ ФИГУРЫ РАВНОВЕЛИКИЕ ФИГУРЫ, плоские фигуры с одинаковыми площадями или геометрические тела с одинаковыми объемами … Энциклопедический словарь

РАВНОВЕЛИКИЕ ФИГУРЫ — плоские фигуры с одинаковыми площадями или геом. тела с одинаковыми объёмами … Естествознание. Энциклопедический словарь

Равновеликие и равносоставленные фигуры — Равновеликие фигуры плоские (пространственные) фигуры одинаковой площади (объёма); равносоставленные фигуры фигуры, которые можно разрезать на одинаковое число соответственно конгруэнтных (равных) частей. Обычно понятие… … Большая советская энциклопедия

РАВНОВЕЛИКИЙ — РАВНОВЕЛИКИЙ, ая, ое; ик. 1. Равный по силе, возможностям, значению (книжн.). Равновеликие явления. 2. равновеликие фигуры (тела) в математике: фигуры (тела), равные по площади или объёму. | сущ. равновеликость, и, жен. Толковый словарь Ожегова.… … Толковый словарь Ожегова

Словарь терминов планиметрии — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И К Л М Н О П Р С … Википедия

Коллинеарные точки — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Конкурентные прямые — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Окружность Аполония — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Источник

РАВНОВЕЛИКИЕ ФИГУРЫ

Смотреть что такое «РАВНОВЕЛИКИЕ ФИГУРЫ» в других словарях:

равновеликие фигуры — плоские фигуры с одинаковыми площадями или геометрического тела с одинаковыми объёмами. * * * РАВНОВЕЛИКИЕ ФИГУРЫ РАВНОВЕЛИКИЕ ФИГУРЫ, плоские фигуры с одинаковыми площадями или геометрические тела с одинаковыми объемами … Энциклопедический словарь

Равновеликие фигуры — Площадь фигуры числовая характеристика фигуры. В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов. Содержание 1 Об определении 2 Связанные определения 3 Комментарии … Википедия

РАВНОВЕЛИКИЕ ФИГУРЫ — плоские фигуры с одинаковыми площадями или геом. тела с одинаковыми объёмами … Естествознание. Энциклопедический словарь

Равновеликие и равносоставленные фигуры — Равновеликие фигуры плоские (пространственные) фигуры одинаковой площади (объёма); равносоставленные фигуры фигуры, которые можно разрезать на одинаковое число соответственно конгруэнтных (равных) частей. Обычно понятие… … Большая советская энциклопедия

РАВНОВЕЛИКИЙ — РАВНОВЕЛИКИЙ, ая, ое; ик. 1. Равный по силе, возможностям, значению (книжн.). Равновеликие явления. 2. равновеликие фигуры (тела) в математике: фигуры (тела), равные по площади или объёму. | сущ. равновеликость, и, жен. Толковый словарь Ожегова.… … Толковый словарь Ожегова

Словарь терминов планиметрии — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И К Л М Н О П Р С … Википедия

Коллинеарные точки — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Конкурентные прямые — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Окружность Аполония — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Источник