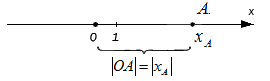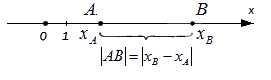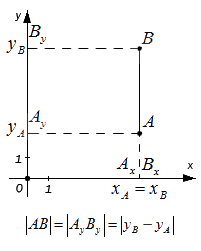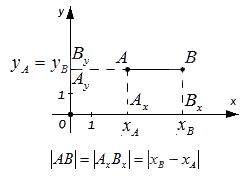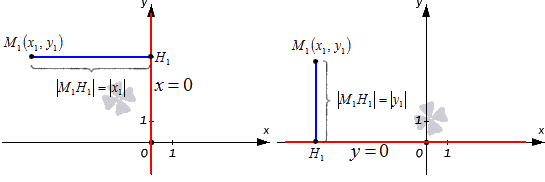что такое расстояние в геометрии

08.12.202327.04.2022 admin 0 Comments

61. Стереометрия Читать 0 мин.

61.333. Расстояния

Расстояния

Задача на нахождения расстояния в стереометрической фигуре является главной и самой важной из всех. Прежде всего определимся с тем, что имеется ввиду под словом «расстояние», ведь их может быть бесконечно много.

Расстояние между объектами в геометрии – это кратчайшее из расстояний между ними.

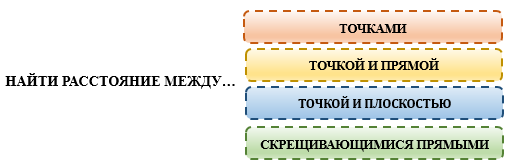
В стереометрии найти расстояние можно между следующими комбинациями фигур:

РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ

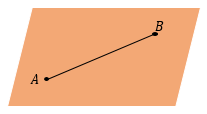
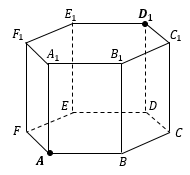
Расстояние между точками– это длина отрезка, соединяющего эти точки.

В задачах на стереометрию мы не можем просто воспользоваться линейкой, и длину этого отрезка должны найти аналитически. Поэтому длину отрезка AB между точками A и B находят как сторону треугольника, если отрезок AB удается включить в некоторый треугольник в качестве одной из его сторон.

То есть если в задаче предлагается найти расстояние между точками, нужно задать себе вопрос: «В каком треугольнике этот отрезок является стороной?», затем построить этот треугольник и найти в нем нужную сторону.

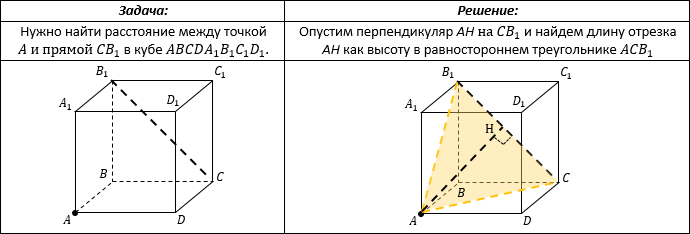
РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ И ПРЯМОЙ

Расстояние от точки до прямой – длина перпендикуляра, опущенного из точки на прямую.

Этот отрезок перпендикуляра можно вычислить, включив его в треугольник (или трапецию) в качестве одной из высот. То есть нужно задать себе вопрос: «В каком треугольнике этот отрезок является высотой?», затем построить этот треугольник и найти в нем высоту.

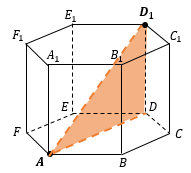
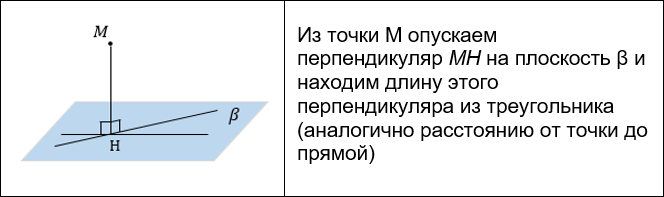
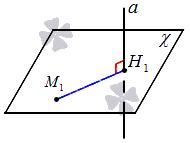
РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ И ПЛОСКОСТЬЮ

Существует несколько способов нахождения расстояния от точки до плоскости:

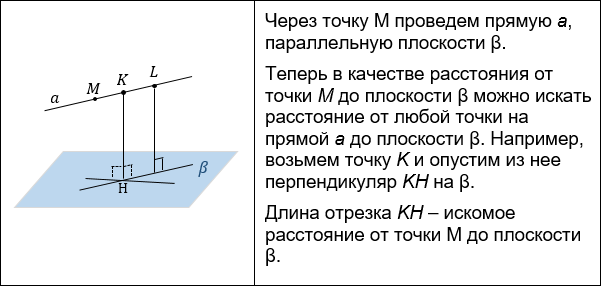
К этому способу, аналогично, обращаются, если расстояние из точки M на плоскость опускать неудобно, а удобно опустить равный ему перпендикуляр из другой точки, лежащей на одной плоскости с M.

Расстояние от точки M до плоскости β – это перпендикуляр, опущенный из точки на плоскость, то есть по сути это высота в некоторой пирамиде с вершиной M и плоскостью основания, лежащей на β. Если легко вычислить объем этой пирамиды, используя другое основание и другую высоту, то через этот объем можно найти нужное расстояние.

РАССТОЯНИЕ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ

Существует несколько способов нахождения расстояния между скрещивающимися прямыми:

1. Построение взаимного перпендикуляра.

2. Построение параллельной прямой.

К этому способу обращаются, если строить взаимный перпендикуляр неудобно и одна из скрещивающихся прямых уже заключена в удобную плоскость.

К этому способу обращаются, если строить взаимный перпендикуляр неудобно и скрещивающиеся прямые уже заключены в удобные плоскости.

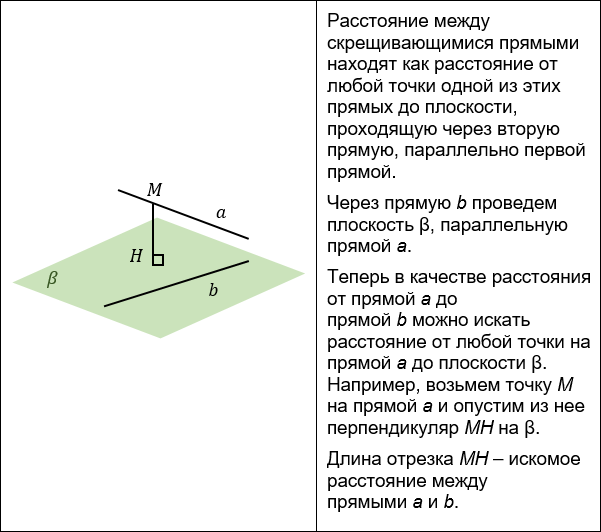
3. Построение параллельной плоскости.

Источник

Расстояние от точки до точки: формулы, примеры, решения

В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения.

Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе. Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.

Расстояние между точками на координатной прямой

В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.

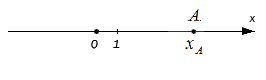
Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой О А отрезки – единицы длины, мы можем определить длину отрезка O A по итоговому количеству отложенных единичных отрезков.

Резюмируя: расстояние от начала отсчета до точки, которой соответствует действительное число на координатной прямой, равно:

При этом очевидно, что сама длина отрезка не может быть отрицательной, поэтому, используя знак модуля, запишем расстояние от точки O до точки A с координатой x A : O A = x A

Расстояние между точками на плоскости

— если точки А и В совпадают, то расстояние между ними равно нулю;

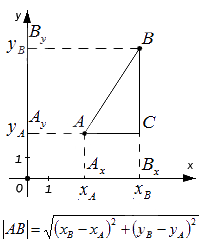
— если точки A и B не лежат на прямой, перпендикулярной одной из координатных осей, найдем расстояние между ними, выведя формулу расчета:

Сформируем вывод из полученного результата: расстояние от точки А до точки В на плоскости определяется расчётом по формуле с использованием координат этих точек

Для ситуации, когда точки A и B лежат на прямой, перпендикулярной оси абсцисс:

Для случая, когда точки A и B лежат на прямой, перпендикулярной оси ординат:

Расстояние между точками в пространстве

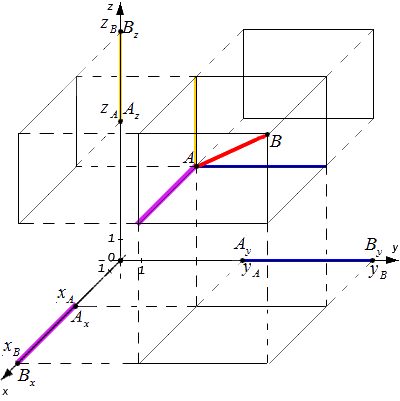
Из курса геометрии известно, что квадрат диагонали параллелепипеда равен сумме квадратов его измерений. Исходя из этого утверждения получим равенство: A B 2 = A x B x 2 + A y B y 2 + A z B z 2

Используя полученные ранее выводы, запишем следующее:

Итоговая формула для определения расстояния между точками в пространстве будет выглядеть следующим образом:

Полученная формула действительна также для случаев, когда:

— лежат на одной координатной оси или прямой, параллельной одной из координатных осей.

Примеры решения задач на нахождение расстояния между точками

Решение

А также используем имеющееся условие, что А В = 5 и тогда будет верным равенство:

λ 2 + 16 = 5 λ 2 + 16 = 25 λ = ± 3

Решение

Источник

Расстояние от точки до прямой на плоскости и в пространстве: определение и примеры нахождения

Данная статья рассказывает о теме «расстояния от точки до прямой», рассматриваются определения расстояния от точки к прямой с иллюстрированными примерами методом координат. Каждый блок теории в конце имеет показанные примеры решения подобных задач.

Расстояние от точки до прямой – определение

Расстояние от точки до прямой находится через определение расстояния от точки до точки. Рассмотрим подробней.

Бывают записи определения с фигурированием длины перпендикуляра.

Расстоянием от точки до прямой называют длину перпендикуляра, проведенного из данной точки к данной прямой.

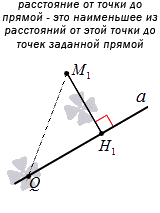
Определения эквивалентны. Рассмотрим рисунок, приведенный ниже.

Известно, что расстояние от точки до прямой является наименьшим из всех возможных. Рассмотрим это на примере.

Расстояние от точки до прямой на плоскости – теория, примеры, решения

Исходные данные для нахождения от точки до прямой позволяют использовать несколько методов решения: через теорему Пифагора, определения синуса, косинуса, тангенса угла и другими. Большинство заданий такого типа решают в школе на уроках геометрии.

Когда при нахождении расстояния от точки до прямой можно ввести прямоугольную систему координат, то применяют метод координат. В данном пункте рассмотрим основных два метода нахождения искомого расстояния от заданной точки.

Теорема способна помочь ответить на вопрос о нахождении расстояния от заданной точки до заданной прямой на плоскости.

Решение задач на нахождение расстояния от заданной точки до заданной прямой на плоскости

Применим данные методы на решении задач с нахождением расстояния от точки до плоскости.

Применим первый способ для решения.

Второй способ решения.

Видно, что в данном методе важно использование нормального уравнения прямой, так как такой способ является наиболее коротким. Но первый метод удобен тем, что последователен и логичен, хотя имеет больше пунктов вычисления.

Решение первым способом подразумевает приведение заданного уравнения с угловым коэффициентом к уравнению общего вида. Для упрощения можно сделать иначе.

Расстояние от точки до прямой в пространстве – теория, примеры, решения

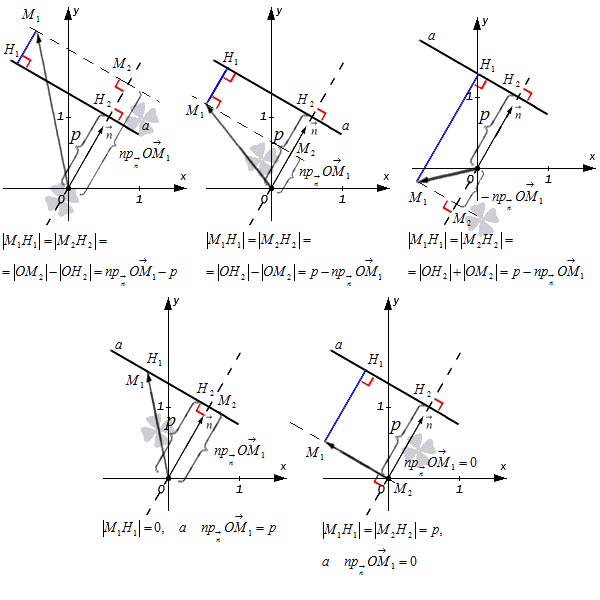
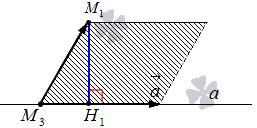
Рассмотрим на рисунке, приведенном ниже.

Решение задач на нахождение расстояния от заданной точки до заданной прямой в пространстве

Имеются все данные для использования формулы вычисления расстояния от точки для прямлой, поэтому применим ее и получим:

M 1 H 1 = a → × M 3 M 1 → a → = 330 30 = 11

Источник

Расстояние от точки до прямой — формулы и способы определения

Вычисление расстояния от точки до прямой является одной из часто встречающихся задач по геометрии в старших классах школ. Известна универсальная формула для их решения, однако ее использование требует умения применять операции над векторами. Разработанные способы определения расстояния между геометрическими элементами справедливы для случаев на плоскости и в трехмерном пространстве.

Точка и прямая

Прежде чем говорить, как найти расстояние от прямой до точки, необходимо подробно рассмотреть, о каких элементах идет речь.

Известно, что в двумерном или трехмерном пространстве в геометрии для определения места расположения того или иного объекта вводится специальная система координат. Удобнее всего использовать прямоугольную декартову систему, которая представляет собой пересекающиеся под прямым углом оси (2 для плоскости и 3 для трехмерного пространства). На каждой из них существует шкала в выбранных единицах.

Обычно она является равномерной, то есть на каждой оси единица представляет собой отрезок одинаковой длины.

Точечный объект

Или просто точка. Это нульмерный объект, который в двумерном пространстве представляет собой набор двух координат, а в трехмерном — трех. Математически точка записывается так: A (x1; y1), где x1 — ее координата по оси x, y1 — по оси y. Для определения значения координат необходимо от точки провести перпендикуляр к соответствующей оси, их пересечение укажет на искомое значение. Примеры разных точек на плоскости и пространстве:

Точка P лежит на оси x, а M в начале координатной системы. Обе они заданы на плоскости, в отличие от Q и N, которые можно построить в пространстве. Также следует отметить, что у координатных осей имеется положительное и отрицательное направления, поэтому точки могут иметь отрицательные координаты.

Уравнения линии

Прямая линия является одним из самых распространенных объектов в геометрии. С помощью нее строятся многие симметричные фигуры, например, пирамида, призма, треугольник, прямоугольник (но не сфера). Прямая линия представляет собой бесконечный объект в одном направлении, и нульмерный в двух других, если речь идет об объемном пространстве.

Для выполнения математических операций с геометрическим элементом существуют разные виды уравнений, которые его задают. Среди них можно назвать:

Чаще всего в задачах применяют первые 2 вида. Универсальным уравнением, которое можно с легкостью преобразовать в любые другие формы, является векторное. Задается для трехмерного случая оно следующим образом:

(x; y; z) = (x0; y0; z0) + α*(vx; vy; vz).

Здесь (x; y; z) — координаты произвольной точки, которая принадлежит заданной прямой, (x0; y0; z0) — известная точка, лежащая на объекте, v (vx; vy; vz) — вектор, параллельно которому проходит прямая, он называется направляющим, α — произвольный числовой параметр, который может иметь положительные или отрицательные значения. Очевидно, что для плоского случая количество координат для каждого элемента будет равно двум.

Векторным уравнением удобно пользоваться, поскольку его легко преобразовать в параметрическое или в отрезках. В первом случае получается следующая система:

Для уравнения в отрезках получается такое равенство:

(x-x0)/vx = (y-y0)/vy = (z-z0)/vz.

Чтобы получить из векторной формы уравнение общего типа для случая на плоскости, достаточно написать выражение в отрезках, а затем из него выразить y через x. В итоге получается такой вид:

Для трехмерного пространства также можно использовать этот математический прием, однако придется выражать не только y через x, но и z через, например, y. Дело в том, что в объемном пространстве прямая задается в общем виде как пересечение двух плоскостей.

Способы определения расстояния

В первую очередь необходимо понять, что называется дистанцией между точкой и прямой линией. Пусть имеется прямая a и точка A. Если из нульмерного объекта провести отрезок к прямой так, чтобы ее он пересекал под прямым углом в некоторой точке A1, то AA1 будет называться перпендикуляром к a. Согласно определению, расстояние от точки до прямой равно длине перпендикулярного отрезка, опущенного из нульмерного объекта к одномерному.

Из геометрических представлений понятно, что длина AA1 будет наименьшей среди всех возможных отрезков, которые можно провести от A к a.

Применение векторных выражений

После получения представлений, что понимают под дистанцией между геометрическими объектами, в докладе можно переходить к рассмотрению первого универсального способа решения этой задачи.

Пусть имеется прямая, заданная в векторной форме в двумерном пространстве: (x; y) = (x0; y0) + α*(vx; vy).

В этой же координатной системе задана точка P (x1; y1). В первую очередь необходимо найти вектор u (ux; uy), который будет перпендикулярен направляющему v (vx; vy). Сделать это несложно, если вспомнить, что скалярное произведение перпендикулярных векторов равно нулю. В итоге получается следующее выражение:

Подставляя в это равенство произвольное значение uy, можно получить координату ux. Если одна из координат вектора v равна нулю, например, vx=0, тогда uy=0 для любых значений ux отличных от 0.

Зная координаты направляющего вектора u для перпендикуляра, можно построить для него векторное уравнение прямой, которая будет проходить через P:

(x; y) = (x1; y1) + β *(ux; uy).

Теперь необходимо найти точку пересечения обеих прямых. Для этого можно выразить y через x для каждой из них, а затем, решить систему из двух линейных уравнений. Например, получилась точка Q (x2; y2).

Для решения задачи остается сделать последний шаг: найти длину отрезка, заключенного между точками P и Q. Искомая формула имеет вид:

PQ = ((x2-x1)^2 + (y2-y1)^2)^0,5.

Описанный способ определения дистанции от прямой до точки можно использовать для задач на плоскости. Дело в том, что в трехмерном пространстве существует бесконечное количество перпендикуляров заданной прямой, поэтому для трехмерного случая придется вводить еще одно условие на поиск перпендикулярного отрезка: он должен лежать в плоскости, проходящей через заданные прямую и точку. Этот факт усложняет решение задачи.

Использование формулы

Применение известной формулы для решения геометрических проблем является самым простым способом. Пусть имеется некоторая прямая, которая в векторной форме задается так:

(x; y; z) = (x0; y0; z0) + α*(vx; vy; vz).

Известна также точка P (x1; y1; z1). Теперь следует выбрать произвольную точку на прямой, пусть это будет Q (x2; y2; z2). Следует отметить, что координаты Q удовлетворяют векторному уравнению заданной прямой. Далее, нужно построить вектор PQ, его координаты определяются так:

PQ = (x2-x1; y2-y1; z2-z1).

После этого следует рассмотреть параллелограмм, который однозначно может быть построен на векторах PQ и v (vx; vy; vz) — направляющий отрезок заданной прямой линии (для наглядности фигуру можно изобразить на рисунке). Известно, что площадь параллелограмма может быть определена двумя способами:

Поскольку оба выражения используются для нахождения одной и той же площади S, их можно приравнять и выразить высоту h:

Поскольку высота параллелограмма является искомой дистанцией d от точки P до заданной в задаче прямой, получается следующая простая формула:

Вычисление векторного произведения проще всего выполнять с помощью матрицы и алгебраического дополнения (стандартная операция вычисления определителя). Удобство полученной формулы заключается в ее универсальности, то есть она применима как для трехмерного пространства, так и для случая на плоскости. Для двумерной задачи в координатной форме выражение примет вид:

d = ((x2-x1)*vy+(y2-y1)*vx)/ (vx 2 + vy 2 )^0,5.

Это выражение является несколько громоздким, поэтому рекомендуется запомнить только его векторную форму.

Решение задачи

Для начала нужно находить направляющий вектор прямой. Его координаты будут соответствовать следующим значениям:

Теперь следует найти вектор AC:

AC = C — A = ((-1−1); (1−0)) = (-2; 1).

Прежде чем воспользоваться формулой для определения расстояния, можно заранее вычислить модуль векторного произведения [AB*AC] и длину AB:

Тогда дистанция d от точки C до прямой, проходящей через A и B будет равно:

Таким образом, для определения расстояния между известными прямой и точкой в пространстве существует 2 способа.

Первый предполагает использование ряда математических рассуждений с выкладками. Он справедлив только для задач на плоскости. Второй способ позволяет воспользоваться универсальной формулой.

Источник