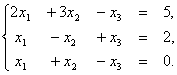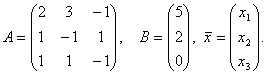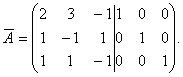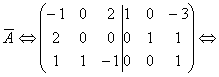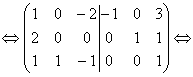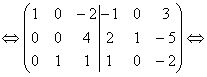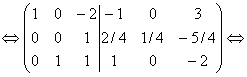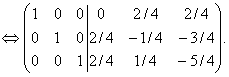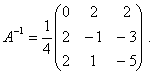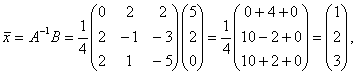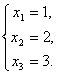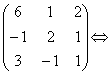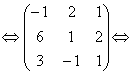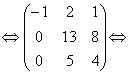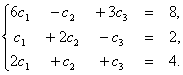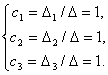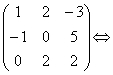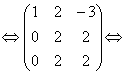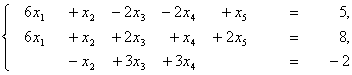что такое ранг системы векторов
Что такое ранг системы векторов
1.4. РАНГ СИСТЕМЫ ВЕКТОРОВ
Рассмотрим систему векторов (1.1), где 
. Максимальной линейно независимой подсистемой системы векторов (1.1) называется любой набор векторов последней, удовлетворяющий следующим условиям: векторы этого набора линейно независимы; всякий вектор из системы (1.1) линейно выражается через векторы этого набора. В общем, система векторов (1.1) может иметь несколько разных максимальных линейно независимых подсистем.
Теорема 1. 6. Все максимальные линейно независимые подсистемы данной системы векторов содержат одно и то же число векторов.
Число векторов в максимальной линейно независимой подсистеме системы векторов (1.1) называется рангом последней. Системы векторов (1.1) и (1.2) называются эквивалентными, если векторы системы (1.1) линейно выражаются через систему векторов (1.2) и наоборот.
Теорема 1. 7. Ранги эквивалентных систем векторов равны.
Операции, переводящие систему векторов (1.1) в систему, ей эквивалентную, следующие:
1) изменение нумерации векторов в системе;
2) удаление нулевого вектора;
3) удаление вектора, являющегося линейной комбинацией остальных векторов системы;
4) умножение произвольного вектора системы на любое, не равное нулю число;
5) прибавление к одному из векторов системы линейной комбинации остальных векторов системы.
Что такое ранг системы векторов
Определение 1. Рангом системы векторов называется максимальное число линейно независимых векторов системы.
.
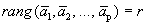
Определение 2. Базисом системы векторов называется максимальная линейно независимая подсистема данной системы векторов.
Теорема. Любой вектор системы можно представить в виде линейной комбинации векторов базиса системы. (Всякий вектор системы можно разложить по векторам базиса.) Коэффициенты разложения определяются для данного вектора и данного базиса однозначно.
.
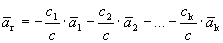
Докажем, что разложение вектора по базису единственно. Предположим противное: имеется два разложения вектора по базису.
Вычитая эти равенства, получим
.
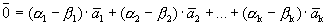
Учитывая линейную независимость векторов базиса, получим
.
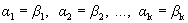
Следовательно, разложение вектора по базису единственно.
Количество векторов в любом базисе системы одинаково и равно рангу системы векторов.
Пример. Дана система векторов: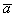 
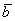
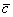
(2, 0), 
(5, 5), 
(4, 3).
Что такое ранг системы векторов
Найдем обратную матрицу к матрице А. Составим расширенную матрицу и с помощью элементарных преобразований приведем ее левую часть к единичной матрице.
Возьмем третью строку. Сложим ее со второй строкой и сложим с первой строкой, умножив на (-3).
умножим первую строку на (-1):
возьмем первую строку. Умножим ее на (-2), сложим со второй строкой и сложим с третьей строкой, умножив первую строку на (-1):
разделим вторую строку на (4)
возьмем вторую строку. Умножим ее на 2 и сложим с первой строкой и сложим с третьей строкой, умножив вторую строку на (-1):
переставим две последние строки:
В левой части расширенной матрицы получена единичная матрица, следовательно, в правой части получена обратная матрица.
Найдем решение системы.
1 (6,1,2), 2 (-1,2,1), 3 (3,-1,1);
1 (1,2,-3), 2 (-1,0,5), 3 (0,2,2).
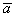
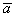
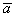
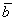
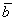
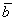
Найти ранги данных систем и выяснить, какая из них образует базис. Найти координаты вектора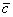 
(8, 2, 4) в этом базисе с помощью формул Крамера.
Решение. Составим матрицу из координат векторов первой системы и найдем ее ранг. Для этого приведем ее к треугольному виду.
переставим первые две строки
умножим первую строку на 6 и сложим со второй, умножим первую строку на 3 и сложим с третьей строкой
разделим вторую строку на 13
умножим вторую строку на (-5) и сложим с третьей
Ранг системы векторов равен 3. Векторы линейно независимы и поскольку их три и они трехмерные, то они образуют базис в трехмерном пространстве. Любой вектор пространства можно разложить по векторам этой системы.
.
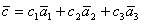
Найдем координаты разложения. Подставим координаты векторов в последнее равенство.
Так как векторы равны, то равны их координаты.
Получена система трех линейных уравнений с тремя неизвестными. Решим ее методом Крамера. Найдем главный определитель системы.
.
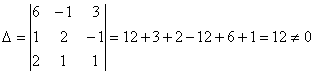
Система имеет единственное решение. Найдем вспомогательные определители. Они получаются из главного определителя заменой соответствующего столбца на столбец свободных членов.
,
,
.
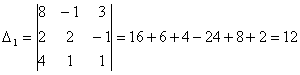
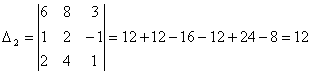
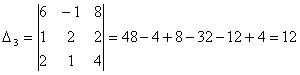
Выпишем решение системы.
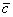
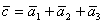
Разложение вектора (8, 2, 4) в данном базисе имеет вид
.
Найдем ранг второй системы векторов. Составим матрицу из координат векторов и приведем ее к треугольному виду.
прибавим первую строку ко второй
умножим вторую строку на (-1) и сложим с третьей
.
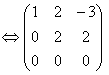
Ранг системы векторов равен 2. Векторы линейно зависимы и они не образуют базиса в трехмерном пространстве.
и сделать переход к другому неотрицательному базисному решению. Выписать общее решение системы.
Решение. 1. Заполняем исходную таблицу. Умножаем третье уравнение на (-1).
Линейная Алгебра
Ранг системы векторов
п.2. Ранг системы векторов.
Пусть V – векторное пространство над полем K, 
– произвольная система векторов пространства V.
Определение. Любое непустое подмножество множества 
называют подсистемой данной системы векторов.
Пример. Пусть дана система векторов 
. Тогда 
, 
, 
– подсистемы данной системы. Сама система тоже является подсистемой самой себя.
Определение. Подсистему называют максимальной линейно независимой подсистемой данной системы векторов, если она линейно независимая и при добавлении к ней любого вектора данной системы становится линейно зависимой.
Определение. Рангом системы векторов называют число векторов в ее максимальной линейно независимой подсистеме.
Обозначение: 
.
Заметим, что если система векторов содержит хотя бы один ненулевой вектор, то ее ранг больше или равен 1.
В дальнейшем предполагаем, что система векторов содержит ненулевой вектор.
Следующая теорема показывает, что ранг системы является ее инвариантом, т.е. не зависит от выбора максимальной линейно независимой подсистемы данной системы векторов.
Теорема. (О ранге системы векторов.) Ранг системы векторов равен размерности линейной оболочки, натянутой на ее векторы, т.е.
. (4)
Доказательство. Для удобства записи перенумеруем векторы системы так, чтобы система 
была максимальной линейно независимой подсистемой данной системы векторов. Тогда 
.
Рассмотрим два случая.
1) 
, т.е. данная система векторов является линейно независимой. Тогда она сама является ее максимальной линейно независимой подсистемой и ее ранг равен m. Рассмотрим линейную оболочку, натянутую на векторы данной системы:
.
Система векторов по определению линейной оболочки является ее порождающей системой и по нашему предположения является линейно независимой. Следовательно, система является базисом линейной оболочки L, а потому ее размерность равна m и равенство (4) доказано.
2) 
. Тогда система векторов 
является линейно зависимой для всех значений индекса 
, откуда следует, что вектор 
линейно выражается через предыдущие векторы этой системы, т.е. 
. Отсюда следует, что
,
п так как обратное включение очевидно, то
,
и 
, ч.т.д.
Следствие. Ранг системы векторов является ее инвариантом, т.е. на зависит от выбора ее максимальной линейно независимой подсистемы.
Доказательство. Пусть произвольная система векторов и 
, 
– две ее произвольные максимальные линейно независимые подсистемы. Тогда, по теореме,
и
, откуда
, ч.т.д.
Замечание. Из последней теоремы следует, что базисом линейной оболочки, натянутой на систему векторов является максимальная линейно независимая подсистема данной системы векторов. Действительно, найденная максимальная линейно независимая подсистема является линейно независимой и число векторов в ней равно размерности линейной оболочки, т.е. она является базисом линейной оболочки.
Ранг и базис системы векторов
.
Определение 2. Базисом системы векторов называется максимальная линейно независимая подсистема данной системы векторов.
Теорема. Любой вектор системы можно представить в виде линейной комбинации (Линейной комбинацией системы векторов называется выражение вида
Доказательство.Пусть система 
имеет базис 
.
1 случай. Вектор 
— из базиса. Следовательно, он равен одному из векторов базиса, допустим 
. Тогда 
= 
.
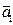
2 случай. Вектор 
— не из базиса. Тогда r>k.
Рассмотрим систему векторов 
. Данная система является линейно зависимой, так как 
— базис, т.е. максимальная линейно независимая подсистема. Следовательно, найдутся числа с1, с2, …, сk, с, не все равные нулю, такие, что 
= 
. Очевидно, что 
(если с=0, то базис системы является линейно зависимым). 
.
Докажем, что разложение вектора по базису единственно. Предположим противное: имеется два разложения вектора по базису.
= 
, = 
.
Вычитая эти равенства, получим 
.
Учитывая линейную независимость векторов базиса, получим 
.
Следовательно, разложение вектора по базису единственно.
Количество векторов в любом базисе системы одинаково и равно рангу системы векторов.
Вычисление ранга системы векторов можно свести к вычислению ранга матрицы. Т.к. ранг системы векторов равен рангу матрицы, столбцами (строками) которой являются векторы этой системы.
Пример. Найти ранг системы векторов
Составим матрицу из координат векторов и найдем ее ранг.
, r(А)=3, 
=1¹0.
Ранг данной системы векторов равен трем, т.е. она имеет три линейно независимых вектора.
Системы линейных уравнений
Определение:Системой 
линейных уравнений с 
неизвестными называется система уравнений вида
 | (1) |
Систему (1) можно записать также в виде
Но наиболее удобной формой записи системы (15.1) является матричная запись. Введем следующие матрицы: матрица системы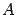 
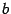
, столбец неизвестных 
и столбец свободных членов 
,
с помощью введенных обозначений систему (1) можно записать в виде
Однородная, неоднородная СЛАУ.
Система уравнений называется однородной, если 
и неоднородной в противном случае.