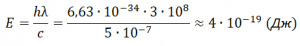что такое работа выхода в фотоэффекте
Фотоэффект
теория по физике 🧲 квантовая физика
Начало теории электромагнитной природы света заложил Максвелл, который заметил сходство в скоростях распространения электромагнитных и световых волн. Но согласно электродинамической теории Максвелла любое тело, излучающее электромагнитные волны, должно в итоге остынуть до абсолютного нуля. В действительности этого не происходит. Противоречия между теорией и опытными наблюдениями были разрешены в начале XX века, вскоре после того, как был открыт фотоэффект.
Что такое фотоэффект
Фотоэффект — испускание электронов из вещества под действием падающего на него света.
Явление фотоэффекта было открыто в 1887 году Генрихом Герцем. Фотоэффект также был подробно изучен русским физиком Александром Столетовым в период с 1888 до 1890 годы. Этому явлению он посвятил 6 научных работ.
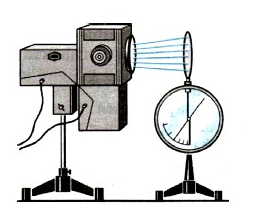
Для наблюдения фотоэффекта нужно провести опыт. Для этого понадобится электрометр и подсоединенная к нему пластинка из цинка (см. рисунок ниже). Если дать пластинке положительный заряд, то при ее освещении электрической дугой скорость разрядки электрометра не изменится. Но если цинковую пластинку зарядить отрицательно, то свет от дуги заставить электрометр разрядиться очень быстро.
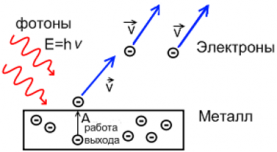
Наблюдаемое во время этого эксперимента явление имеет простое объяснение. Свет вырывает электроны с поверхности цинковой пластинки. Если она имеет отрицательный заряд, электроны отталкиваются от нее, что приводит к полному разряжению электрометра. Причем при повышении интенсивности освещения скорость разрядки увеличивается, ровно, как и наоборот: при уменьшении интенсивности освещения электрометр разряжается медленно. Если же зарядить пластинку положительно, то электроны, которые вырываются светом, притягиваются к ней. Поэтому они оседают на ней, не изменяя заряд электрометра.
Если между световым пучком и отрицательно заряженной пластиной поставить
Явление фотоэффекта может вызвать только ультрафиолетовый участок спектра.
Волновая теория света не может объяснить, почему электроны могут вырываться только под действием ультрафиолета. Ведь даже при большой амплитуде и силе волн электроны остаются на месте, когда, казалось бы, они должны непременно быть вырванными.
Законы фотоэффекта
Чтобы получить более полное представление о фотоэффекте, выясним, от чего зависит количество электронов, вырванных светом с поверхности вещества, а также, от чего зависит их скорость, или кинетическая энергия. Выяснить все это нам помогут эксперименты.
Первый закон фотоэффекта
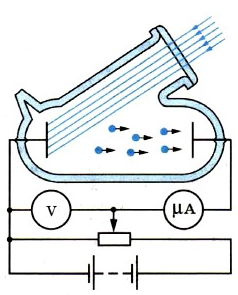
Возьмем стеклянный баллон и выкачаем из него воздух (смотрите рисунок выше). Затем поместим в него два электрода. На электроды подадим напряжение и будем регулировать его с помощью потенциометра и измерять при помощи вольтметра.
В верхней части нашего баллона есть небольшое кварцевое окошко, которое пропускает весь свет, в том числе ультрафиолетовый. Через него падает свет на один из электродов (в нашем случае на левый электрод, к которому присоединен отрицательный полюс батареи). Мы увидим, что под действием света этот электрод начнет испускать электроны, которые при движении в электрическом поле будут создавать электрический ток. Вырванные электроны будут направляться ко второму электроду. Но если напряжение небольшое, второго электрода достигнут не все электроны. Если интенсивность излучения сохранить, но увеличить между электродами разность потенциалов, то сила тока будет увеличиваться. Но как только она достигнет некоторого максимального значения, рост силы тока при дальнейшем увеличении напряжения прекратится. Максимальное значение силы тока будем называть током насыщения.
Ток насыщения — максимальное значение силы тока, также называемое предельным значением силы фототока.
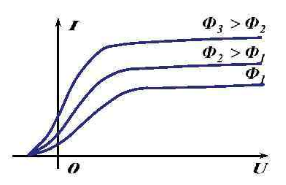
Если же мы начнем изменять интенсивность излучения, то сможем заметить, что фототок насыщения также начинается меняться. Если интенсивность излучения ослабить, максимальное значение силы тока уменьшится. Если интенсивность светового потока увеличить, ток насыщения примет большее значение. Отсюда можно сделать вывод, который называют первым законом фотоэффекта.
Первый закон фотоэффекта:
Число электронов, вырываемых светом с поверхности металла за 1 с, прямо пропорционально поглощаемой за это время энергии световой волны. Иными словами, фототок насыщения прямо пропорционален падающему световому потоку Ф.
Второй закон фотоэффекта
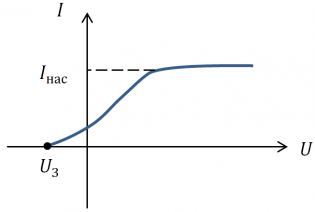
Теперь произведем измерения кинетической энергии, то есть, скорости вырывания электронов. Взгляните на график, представленный ниже. Видно, что сила фототока выше нуля даже при нулевом напряжении. Это говорит о том, что даже при нулевой разности потенциалов часть электронов достигает второго электрода.
Опыт показывает, что при изменении интенсивности света (плотности потока излучения) задерживающее напряжение не меняется. Значит, не меняется кинетическая энергия электронов. С точки зрения волновой теории света этот факт непонятен. Ведь чем больше интенсивность света, тем большие силы действуют на электроны со стороны электромагнитного поля световой волны и тем большая энергия, казалось бы, должна передаваться электронам. Но экспериментальным путем мы обнаруживаем, что кинетическая энергия вырываемых светом электронов зависит только от частоты света. Отсюда мы можем сделать вывод, являющийся вторым законом фотоэффекта.
Второй закон фотоэффекта:
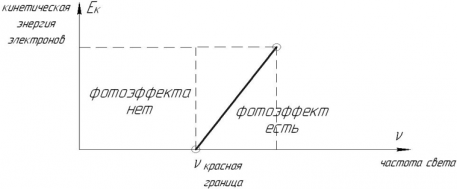
Максимальная кинетическая энергия фотоэлектронов линейно растет с частотой света и не зависит от его интенсивности.
Причем, если частота света меньше определенной для данного вещества минимальной частоты νmin, фотоэффект наблюдаться не будет.
Теория фотоэффекта
Все попытки объяснить явление фотоэффекта электродинамической теорией Максвелла, согласно которой свет — это электромагнитная волна, непрерывно распределенная в пространстве, оказались тщетными. Нельзя было понять, почему энергия фотоэлектронов определяется только частотой света и почему свет способен вырывать электроны лишь при достаточно малой длине волны.
В попытках объяснить это явление физик Макс Планк предложил, что атомы испускают электромагнитную энергию отдельными порциями — квантами, или фотонами. И энергия каждой порции прямо пропорциональна частоте излучения:
h — коэффициент пропорциональности, который получил название постоянной Планка. Она равна 6,63∙10 –34 Дж∙с.
Пример №1. Определите энергию фотона, соответствующую длине волны λ = 5∙10 –7 м.
Энергия фотона равна:
Выразим частоту фотона через скорость света:
Идею Планка продолжил развивать Эйнштейн, которому удалось дать объяснение фотоэффекту в 1905 году. В экспериментальных законах фотоэффекта Эйнштейн увидел убедительное доказательство того, что свет имеет прерывистую структуру и поглощается отдельными порциями. Причем энергия Е каждой порции излучения, по его расчетам, полностью соответствовала гипотезе Планка.
Из того, что свет излучается порциями, еще не вытекает вывода о прерывистости структуры самого света. Ведь и воду продают в бутылках, но отсюда не следует, что вода состоит из неделимых частиц. Лишь фотоэффект позволил доказать прерывистую структуру света: излученная порция световой энергии Е = hν сохраняет свою индивидуальность и в дальнейшем. Поглотиться может только вся порция целиком.
Кинетическую энергию фотоэлектрона можно найти, используя закон сохранения энергии. Энергия порции света hν идет на совершение работы выхода А и на сообщение электрону кинетической энергии. Отсюда:
Работа выхода — минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл.
Полученное выражение объясняет основные факты, касающиеся фотоэффекта. Интенсивность света, по Эйнштейну, пропорциональна числу квантов (порций) энергии hν в пучке света и поэтому определяет количество вырванных электронов. Скорость же электронов согласно зависит только от частоты света и работы выхода, которая определяется типом металла и состоянием его поверхности. От интенсивности освещения кинетическая энергия фотоэлектронов не зависит.
Для каждого вещества фотоэффект наблюдается лишь при освещении его светом с минимальной частотой волны νmin. Это объясняется тем, что для вырывания электрона без сообщения ему скорости нужно выполнять как минимум работу выхода. Поэтому энергия кванта должна быть больше этой работы:
Предельную частоту νmin называют красной границей фотоэффекта. При этой частоте фотоэффект уже наблюдается.
Красная граница фотоэффекта равна:
Минимальной частоте, при которой возможен фотоэффект для данного вещества, соответствует максимальная длина волны, которая также носит название красной границы фотоэффекта. Это такая длина волны, при которой фотоэффект еще наблюдается. Обозначается она как λmах или λкр.
Максимальная длина волны, при которой еще наблюдается фотоэффект, равна:
Работа выхода А определяется родом вещества. Поэтому и предельная частота vmin фотоэффекта (красная граница) для разных веществ различна. Отсюда вытекает еще один закон фотоэффекта.
Третий закон фотоэффекта:
Для каждого вещества существует максимальная длина волны, при которой фотоэффект еще наблюдается. При больших длинах волн фотоэффекта нет.
Пример №2. Чему равна красная граница фотоэффекта νmin, если работа выхода электрона из металла равна A = 3,3∙10 –19 Дж?
Применим формулу для вычисления красной границы фотоэффекта:
Работа выхода
Работа выхода — разница между минимальной энергией (обычно измеряемой в электрон-вольтах), которую необходимо сообщить электрону для его «непосредственного» удаления из объёма твёрдого тела, и энергией Ферми. Здесь «непосредственность» означает то, что электрон удаляется из твёрдого тела через данную поверхность и перемещается в точку, которая расположена достаточно далеко от поверхности по атомным масштабам (чтобы электрон прошёл весь двойной слой), но достаточно близко по сравнению с размерами макроскопических граней кристалла. При этом пренебрегают дополнительной работой, которую необходимо затратить на преодоление внешних полей, возникающих из-за перераспределения поверхностных зарядов. Таким образом, работа выхода для одного и того же вещества для различных кристаллографических ориентаций поверхности оказывается различной.
При удалении электрона на бесконечность его взаимодействие с зарядами, остающимися внутри твёрдого тела приводит к индуцированию макроскопических поверхностных зарядов (при рассмотрении полубесконечного образца в электростатике это называют «изображением заряда»). При перемещении электрона в поле индуцированного заряда совершается дополнительная работа, которая определяется диэлектрической проницаемостью вещества, геометрией образца и свойствами других поверхностей. За счет этого полная работа по перемещению электрона из любой точки образца в любую другую точку (в том числе и точку бесконечности) не зависит от пути перемещения, то есть от того, через какую поверхность был удален электрон. Поэтому в физике твёрдого тела эта работа не учитывается и не входит в работу выхода.
Содержание
Работа выхода в фотоэффекте
Измерение работы выхода
Единицами измерения работы выхода являются Джоуль (Дж) или электронвольт (эВ).
Работа выхода электрона из различных металлов
Единица измерения: эВ электронвольт
Источник: CRC Handbook of Chemistry and Physics version 2008, стр. 12-114.
Примечание: Работа выхода может зависеть от ориентации освещаемого кристалла. К примеру, Ag: 4.26, Ag(100): 4.64, Ag(110): 4.52, Ag(111): 4.74. Диапазоны изменения работы выхода для типичных кристаллографических направлений указаны в таблице.
| Элемент | эВ | Элемент | эВ | Элемент | эВ | Элемент | эВ | Элемент | эВ |
|---|---|---|---|---|---|---|---|---|---|
| Ag: | 4.52 – 4.74 | Al: | 4.06 – 4.26 | As: | 3.75 | Au: | 5.1 – 5.47 | B: | |
| Ba: | 2.52 – 2.7 | Be: | 4.98 | Bi: | 4.31 | C: | Ca: | 2.87 | |
| Cd: | 4.08 | Ce: | 2.9 | Co: | 5 | Cr: | 4.5 | Cs: | 2.14 |
| Cu: | 4.53 – 5.10 | Eu: | 2.5 | Fe: | 4.67 – 4.81 | Ga: | 4.32 | Gd: | 2.90 |
| Hf: | 3.9 | Hg: | 4.475 | In: | 4.09 | Ir: | 5.00 – 5.67 | K: | 2.29 |
| La: | 3.5 | Li: | 2.93 | Lu: | Mg: | 3.66 | Mn: | 4.1 | |
| Mo: | 4.36 – 4.95 | Na: | 2.36 | Nb: | 3.95 – 4.87 | Nd: | 3.2 | Ni: | 5.04 – 5.35 |
| Os: | 5.93 | Pb: | 4.25 | Pd: | 5.22 – 5.6 | Pt: | 5.12 – 5.93 | Rb: | 2.261 |
| Re: | 4.72 | Rh: | 4.98 | Ru: | 4.71 | Sb: | 4.55 – 4.7 | Sc: | 3.5 |
| Se: | 5.9 | Si: | 4.60 – 4.85 | Sm: | 2.7 | Sn: | 4.42 | Sr: | |
| Ta: | 4.00 – 4.80 | Tb: | 3.00 | Te: | 4.95 | Th: | 3.4 | Ti: | 4.33 |
| Tl: | U: | 3.63 – 3.90 | V: | 4.3 | W: | 4.32 – 5.22 | Y: | 3.1 | |
| Yb: | 2.60 [1] | Zn: | 3.63 – 4.9 | Zr: | 4.05 |
Литература
Полезное
Смотреть что такое «Работа выхода» в других словарях:
РАБОТА ВЫХОДА — энергия Ф, к рую необходимо затратить для удаления эл на из твёрдого или жидкого в ва в вакуум (в состояние с равной нулю кинетич, энергией). Р. в. Ф=еj, где j потенциал Р. в., е абс. величина электрич. заряда электрона. Р. в. равна разности… … Физическая энциклопедия
работа выхода — электрона; работа выхода Работа, соответствующая разности энергий между уровнем химического потенциала в теле и уровнем потенциала вблизи поверхности тела вне его при отсутствии электрического поля … Политехнический терминологический толковый словарь
РАБОТА ВЫХОДА — работа, которую необходимо затратить для удаления электрона из конденсированного вещества в вакуум. Измеряется разностью между минимальной энергией электрона в вакууме и Ферми энергией электронов внутри тела. Зависит от состояния поверхности… … Большой Энциклопедический словарь
РАБОТА ВЫХОДА — РАБОТА ВЫХОДА, энергия, затрачиваемая на удаление электрона из вещества. Учитывается при ФОТОЭЛЕКТРИЧЕСКОМ ЭФФЕКТЕ и в ТЕРМОЭЛЕКТРОНИКЕ … Научно-технический энциклопедический словарь
работа выхода — Энергия, необходимая для переноса в бесконечность электрона, находящегося в исходном положении на уровне Ферми в данном материале. [ГОСТ 13820 77] Тематики электровакуумные приборы … Справочник технического переводчика
работа выхода — [work function] энергия, затрачиваемая на удаление электрона из твердого тела или жидкости в вакуум. Переход электрона из вакуума в конденсированную среду сопровождается выделением энергии, равной работе выхода; чем меньше работа выхода, тем… … Энциклопедический словарь по металлургии
работа выхода — работа, которую необходимо затратить для удаления электрона из конденсированного вещества в вакуум. Измеряется разностью между минимальной энергией электрона в вакууме и ферми энергией электронов внутри тела. Зависит от состояния поверхности… … Энциклопедический словарь
работа выхода — išlaisvinimo darbas statusas T sritis Standartizacija ir metrologija apibrėžtis Darbas, kurį atlieka 1 molis dalelių (atomų, molekulių, elektronų) pereidamas iš vienos fazės į kitą arba į vakuumą. atitikmenys: angl. work function vok.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
работа выхода — išlaisvinimo darbas statusas T sritis fizika atitikmenys: angl. work function; work of emission; work of exit vok. Ablösearbeit, f; Auslösearbeit, f; Austrittsarbeit, f rus. работа выхода, f pranc. travail de sortie, m … Fizikos terminų žodynas
48.219. Фотоэффект
Свет обладает двойственной природой: в некоторых случаях он ведет себя как волна, в других ― как частица. При фотоэффекте свет ведет себя как частица. «Порции» света (кванты) ― фотоны. Энергия одного фотона прямо пропорциональна его частоте и равна Ev = hv, где
h ― постоянная Планка, равная 6,6 ∙ 10-34 [Дж∙с];
Фотоэффект (фотоэлектрический эффект) ― испускание электронов веществом под действием света.
Свет поглощают электроны, свободно расположенные в металле. Поглотив квант света, электрон увеличивает свою энергию настолько, что может вылететь из металла. Таким образом, фотоны «выбивают» электроны из металла, если их энергия достаточно велика для этого. Электроны, вылетевшие под действием света (фотонов) называются фотоэлектронами. Поскольку ток ― это направленный поток заряженных частиц ― то при облучении металла светом достаточной энергии, создается ток, который называется фототоком.
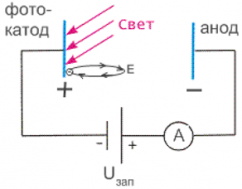
Металлическая пластинка, подключенная к электрической цепи, и облучаемая светом, называется фотокатодом.
Энергия и скорость вылетающих электронов зависит от частоты падающего света ― т. е энергии фотона, который выбивает электрон. Скорость фотоэлектронов тем выше, чем выше частота фотонов. Аналогично, скорость фотоэлектронов тем меньше, чем меньше частота падающих фотонов.
Энергия и скорость вылетающих электронов от интенсивности света не зависят.
Дело в том, что интенсивность (яркость) света определяет не то, какую энергию имеют фотоны (напомним, что энергия фотонов зависит от их частоты), а то, сколько будет этих фотов в свете. Если свет яркий ― в нём находится много фотонов, если свет не яркий ― не много.
Теоретически фотоэффект объяснил Эйнштейн. Формула Эйнштейна для фотоэффекта связывает энергию падающих фотонов и энергию вылетающих электронов: hv = A + EК, где
h ― постоянная Планка, равная 6,6 ∙ 10-34 [Дж∙с];
EК ― кинетическая энергия фотона. [Дж].
Работа выхода фотоэффекта ― постоянная величина и зависит только от природы металла и состояния его поверхности. Работа выхода не зависит от частоты или интенсивности света.
Как видно из формулы Эйнштейна, энергия фотона идет на совершение работы выхода и на увеличение кинетической энергии электрона. Так как работа выхода постоянна, то при уменьшении частоты света ― уменьшается кинетическая энергия, а значит, и скорость вылетающих электронов. Если частота света уменьшается до предельной величины ― частоты красной границы фотоэффекта, скорость электронов становится равной нулю и фотоэффект прекращается. Если частота света меньше частоты красной границы фотоэффекта ― то фотоэффект не наблюдается, поскольку энергии фотонов недостаточно для того, чтобы выбить электрон из материала.
h ― постоянная Планка, равная 6,6 ∙ 10-34 [Дж∙с];
vкрасная граница ― частота света [Гц];
График зависимости кинетической энергии вылетающих электронов от частоты падающих фотонов:
Запирающее напряжение ― это напряжение, не позволяющее электронам покинуть фотокатод. Если напряжение в цепи больше или равно запирающему напряжению, то электроны не могут достигнуть анода: даже если они покидают ненадолго фотокатод, сила электрического поля возвращает их в металл ― и фототока в цепи нет.
Запирающее напряжение определяется выражением eUзап = Eкинетическая, где
e ― заряд электрона равный 1,6 ∙ 10-19 [Кл];
Uзап ― запирающее напряжение [В];
Eкинетическая ― кинетическая энергия фотоэлектрона [Дж].
Когда напряжение в цепи равно нулю U = 0, а фотокатод облучается светом достаточной энергии, чтоб создавать фотоэффект, ― в сети есть ток, его вызывают выбиваемые светом электроны.
Когда напряжение в цепи равно запирающему напряжению U = Uз ― сила тока становится равной нулю, т. к. фототок прекращается.
Как видно из формулы, запирающее напряжение зависит только от кинетической энергии электронов, которая, в свою очередь, зависит от частоты света (но не интенсивности) и работы выхода.
Физика. 11 класс
Конспект урока
Урок 22. Фотоэффект
Перечень вопросов, рассматриваемых на уроке:
Фотоэффект – это вырывание электронов из вещества под действием света.
Работа выхода – это минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл. которую нужно сообщить электрону, для того чтобы он мог преодолеть силы, удерживающие его внутри металла.
Красная граница фотоэффекта – это минимальная частота или максимальная длина волны света излучения, при которой еще возможен внешний фотоэффект.
Основная и дополнительная литература по теме урока:
1. Мякишев Г. Я., Буховцев Б. Б., Чаругин В. М. Физика. 11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 259 – 267.
2. Рымкевич А. П. Сборник задач по физике. 10-11 класс.- М.:Дрофа,2009. – С. 153 – 158.
4. Тульчинский М. Е. Качественные задачи по физике в средней школе. Пособие для учителей. Изд. 4-е, переработ. и доп. М. «Просвещение», 1972. С. 157.
Теоретический материал для самостоятельного изучения
В начале 20-го века в физике произошла величайшая революция. Попытки объяснить наблюдаемые на опытах закономерности распределения энергии в спектрах теплового излучения оказались несостоятельными. Законы электромагнетизма Максвелла неожиданно «забастовали». Противоречия между опытом и практикой были разрешены немецким физиком Максом Планком.
Гипотеза Макса Планка: атомы испускают электромагнитную энергию не непрерывно, а отдельными порциями – квантами. Энергия Е каждой порции прямо пропорциональна частоте ν излучения света: E = hν.
Коэффициент пропорциональности получил название постоянной Планка, и она равна:
После открытия Планка начала развиваться самая современная и глубокая физическая теория – квантовая физика.
Поведение всех микрочастиц подчиняется квантовым законам. Но впервые квантовые свойства материи были обнаружены именно при исследовании излучения и поглощения света.
В 1886 году немецкий физик Густав Людвиг Герц обнаружил явление электризации металлов при их освещении.
Явление вырывания электронов из вещества под действием света называется внешним фотоэлектрическим эффектом.
Законы фотоэффекта были установлены в 1888 году профессором московского университета Александром Григорьевичем Столетовым.
Схема установки для изучения законов фотоэффекта
Зависимость силы тока от приложенного напряжения
Увеличение интенсивности света означает увеличение числа падающих фотонов, которые выбивают с поверхности металла больше электронов.
Второй закон фотоэффекта: максимальная кинетическая энергия фотоэлектронов не зависит от интенсивности падающего излучения и линейно возрастает с увеличением частоты падающего излучения.
Третий закон фотоэффекта: для каждого вещества существует граничная частота такая, что излучение меньшей частоты не вызывает фотоэффекта, какой бы ни была интенсивность падающего излучения. Эта минимальная частота излучения называется красной границей фотоэффекта.
где Ав – работа выхода электронов;
h – постоянная Планка;
λкр – длина волны, соответствующая красной границе.
Фотоэффект практически безынерционен: фототок возникает одновременно с освещением катода с точностью до одной миллиардной доли секунды.
Работа выхода – это минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл.
Для большинства веществ фотоэффект возникает только под действием ультрафиолетового облучения. Однако некоторые металлы, например, литий, натрий и калий, испускают электроны и при облучении видимым светом.
Известно, что фототоком можно управлять, подавая на металлические пластины различные напряжения. Если на систему подать небольшое напряжение обратной полярности, «затрудняющее» вылет электронов, то ток уменьшится, так как фотоэлектронам, кроме работы выхода, придется совершать дополнительную работу против сил электрического поля.
Максимальная кинетическая энергия электронов выражается через задерживающее напряжение:
где 
Е – заряд электрона;

Теорию фотоэффекта разработал Альберт Эйнштейн. На основе квантовых представлений Эйнштейн объяснил фотоэффект. Электрон внутри металла после поглощения одного фотона получает порцию энергии и стремится вылететь за пределы кристаллической решетки, т.е. покинуть поверхность твердого тела. При этом часть полученной энергии он израсходует на совершение работы по преодолению сил, удерживающих его внутри вещества. Остаток энергии будет равен кинетической энергии:
В 1921 году Альберт Эйнштейн стал обладателем Нобелевской премии, которая, согласно официальной формулировке, была вручена «за заслуги перед теоретической физикой и особенно за открытие закона фотоэлектрического эффекта».
Примеры и разбор решения заданий
1. Монохроматический свет с длиной волны λ падает на поверхность металла, вызывая фотоэффект. Фотоэлектроны тормозятся электрическим полем. Как изменятся работа выхода электронов с поверхности металла и запирающее напряжение, если уменьшить длину волны падающего света?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Следовательно, при уменьшении длины волны падающего света, запирающее напряжение увеличивается.
2. Красная граница фотоэффекта для вещества фотокатода λ0 = 290 нм. При облучении катода светом с длиной волны λ фототок прекращается при напряжении между анодом и катодом U = 1,5 В. Определите длину волны λ.
Запишем уравнение для фотоэффекта через длину волны:
Условие связи красной границы фотоэффекта и работы выхода:
Запишем выражение для запирающего напряжения – условие равенства максимальной кинетической энергии электрона и изменения его потенциальной энергии при перемещении в электростатическом поле:
Решая систему уравнений (1), (2), (3), получаем формулу для вычисления длины волны λ:
Подставляя численные значения, получаем: λ ≈ 215 нм.