что такое прямой обратный и дополнительный коды
Обратный и дополнительный коды двоичных чисел



Пример перевода
x1=10101-[x1]пр=010101
x2=-11101-[x2]пр=111101
x3=0,101-[x3]пр=0,101
x4=-0,111-[x4]пр=1,111
2) Обратный код числа, используется для выполнения арифметических операций вычитания, умножения, деления, через сложение. Обратный код положительного числа совпадает с его прямым кодом, обратный код отрицательного числа формируется по правилам: в знаковом разряде записывается “1”; цифровые значения меняются на противоположные.
3) Дополнительный код числа, имеет такое же назначение, как и обратный код числа. Формируется по следующим правилам: положительные числа в дополнительном коде выглядят также как и в обратном и в прямом коде, т.е. не изменяются. Отрицательные числа кодируются следующим образом: к обратному коду отрицательного числа (к младшему разряду) добавляется 1, по правилу двоичной арифметики.
Пример перевода
x1=10101-[x1]доп=010101
x2=-11101-[x2]обр=100010+1-[x2]доп=100011
x3=0,101-[x3]доп=0,101
x4=-0,111-[x4]обр=1,000+1-[x4]доп=1,001
Для выявления ошибок при выполнении арифметических операций используются также модифицированные коды: модифицированный прямой; модифицированный обратный; модифицированный дополнительный, для которых под код знака числа отводится два разряда, т.е. “+”=00; ”-”=11. Если в результате выполнения операции в знаковом разряде появляется комбинация 10 или 01 то для машины это признак ошибки, если 00 или 11 то результат верный.
Прямой, дополнительный и обратный коды
Прямой, дополнительный и обратный код числа (создан по запросу).
Далее идет калькулятор, который переводит введенное положительное или отрицательное целое число в двоичный код, а также выводит обратный код этого числа и его дополнительный код. Под калькулятором, как водится, немного теории.
Обновление: Из комментариев становится ясно, что люди не вполне понимают, что делает этот калькулятор. Точнее, что делал — применял алгоритм вычисления дополнительного кода к любому числу. Люди хотят, чтобы он им просто показывал дополнительный код числа. Ну хорошо — теперь при вводе положительного числа калькулятор показывает представление числа в двоичной форме, ибо для него нет обратного и дополнительного кода, а при вводе отрицательного показывает дополнительный и обратный код.
Прямой, дополнительный и обратный код
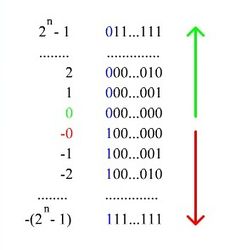
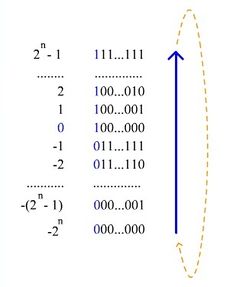
Прямой код числа это представление беззнакового двоичного числа. Если речь идет о машинной арифметике, то как правило на представление числа отводится определенное ограниченное число разрядов. Диапазон чисел, который можно представить числом разрядов n равен
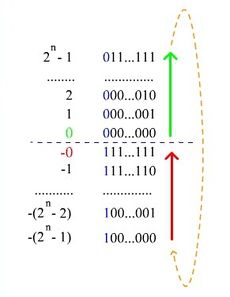
Обратный код числа, или дополнение до единицы (one’s complement) это инвертирование прямого кода (поэтому его еще называют инверсный код). То есть все нули заменяются на единицы, а единицы на нули.
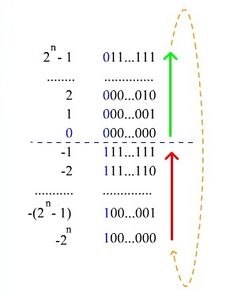
Дополнительный код числа, или дополнение до двойки (two’s complement) это обратный код, к младшему значащему разряду которого прибавлена единица
А теперь «зачем, зачем это все?» ©
Для различия положительных и отрицательных чисел выделяют старший разряд числа, который называется знаковым (sign bit)
0 в этом разряде говорит нам о том, что это положительное число, а 1 — отрицательное.
С положительными числами все вроде бы понятно, для их представления можно использовать прямой код
0 — 0000
1 — 0001
7 — 0111
А как представить отрицательные числа?
И это оказалось очень удобно для машинных вычислений — при таком представлении отрицательного числа операции сложения и вычитания можно реализовать одной схемой сложения, при этом очень легко определять переполнение результата (когда для представления получившегося числа не хватает разрядности)
Пара примеров
7-3=4
0111 прямой код 7
1101 дополнительный код 3
0100 результат сложения 4
-1+7=6
1111 дополнительный код 1
0111 прямой код 7
0110 результат сложения 6
Что касается переполнения — оно определяется по двум последним переносам, включая перенос за старший разряд. При этом если переносы 11 или 00, то переполнения не было, а если 01 или 10, то было. При этом, если переполнения не было, то выход за разряды можно игнорировать.
Примеры где показаны переносы и пятый разряд
00111 прямой код 7
00001 прямой код 1
01110 переносы
01000 результат 8 — переполнение
Два последних переноса 01 — переполнение
-7+7=0
00111 прямой код 7
01001 дополнительный код 7
11110 переносы
10000 результат 16 — но пятый разряд можно игнорировать, реальный результат 0
Два последних переноса 11 з перенос в пятый разряд можно отброс ить, оставшийся результат, ноль, арифметически корректен.
Опять же проверять на переполнение можно простейшей операцией XOR двух бит переносов.
Вот благодаря таким удобным свойствам дополнительный код это самый распространенный способ представления отрицательных чисел в машинной арифметике.
Прямой, обратный и дополнительный коды двоичного числа
Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа

Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.
Прямой код
Обратный код
Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.
Арифметические операции с отрицательными числами в обратном коде:
Дополнительный код
В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).
Арифметические операции с отрицательными числами в дополнительном коде
Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода


Представление целых чисел: прямой код, код со сдвигом, дополнительный код
Выбор способа хранения целых чисел в памяти компьютера — не такая тривиальная задача, как могло бы показаться на первый взгляд. Желательно, чтобы этот способ:
Рассмотрим разные методы представления.
Содержание
Прямой код [ править ]
Достоинства представления чисел с помощью прямого кода [ править ]
Недостатки представления чисел с помощью прямого кода [ править ]
Из-за весьма существенных недостатков прямой код используется очень редко.
Код со сдвигом [ править ]
По сути, при таком кодировании:
Достоинства представления чисел с помощью кода со сдвигом [ править ]
Недостатки представления чисел с помощью кода со сдвигом [ править ]
Из-за необходимости усложнять арифметические операции код со сдвигом для представления целых чисел используется не часто, но зато применяется для хранения порядка вещественного числа.
Дополнительный код (дополнение до единицы) [ править ]
В качестве альтернативы представления целых чисел может использоваться код с дополнением до единицы (англ. Ones’ complement).
Алгоритм получения кода числа:
Достоинства представления чисел с помощью кода с дополнением до единицы [ править ]
Недостатки представления чисел с помощью кода с дополнением до единицы [ править ]
Дополнительный код (дополнение до двух) [ править ]
Чаще всего для представления отрицательных чисел используется код с дополнением до двух (англ. Two’s complement).
Алгоритм получения дополнительного кода числа:
Длинная арифметика для чисел, представленных с помощью кода с дополнением до двух [ править ]
Достоинства представления чисел с помощью кода с дополнением до двух [ править ]
Недостатки представления чисел с помощью кода с дополнением до двух [ править ]
Несмотря на недостатки, дополнение до двух в современных вычислительных системах используется чаще всего.
Коды: прямой, обратный, дополнительный
Коды: прямой, обратный, дополнительный.
В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком: прямой код, обратный код, дополнительный код.. Последние две формы применяются особенно широко, так как позволяют упростить конструкцию арифметико-логического устройства компьютера путем замены разнообразных арифметических операций операцией сложения.
· Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково – с цифрой 0 в знаковом разряде.
ПРИМЕРЫ. Число 110=12: Число 12710=


· Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение.
1. Прямой код. В знаковый ряд помещается цифра 1, а в разряды цифровой части числа – двоичный код его абсолютной величины.


2. Обратный код получается инвентированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяют единицами, а единицы – нулями.
Код модуля числа: 0 0000001. Код модуля числа: 0 1111111
Обратный код числа: 1 1111110. Обратный код числа: 1 0000000
3. Дополнительный код получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду.
ПРИМЕРЫ. Дополнительный код числа-1: Дополнительный код числа-127
Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный двоичный код и в таком виде хранятся, перемещаются и участвуют в операциях. При вводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные числа.
Операция сложения чисел в прямом, обратном и дополнительном кодах выполняется на двоичных сумматорах соответствующего кода.
АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ НАД ЦЕЛЫМИ ЧИСЛАМИ
Сложение и вычитание. В большинстве компьютеров операция вычитания не используется. Вместо неё производится сложение уменьшаемого с обратным или дополнительным кодом вычитаемого. Это позволяет существенно упростить конструкцию АЛУ.
При сложении обратных кодов чисел А и B имеет место четыре основных и два особых случая. Рассмотрим их.
Случай 1. А и В положительные. При суммировании складываются все разряды, включая разряд знака. Так как знаковые разряды положительных слагаемых равны нулю, разряд знака суммы тоже равен нулю.
Десятичная запись: Двоичные коды:
Получен правильный результат.
Случай 2. А положительное, В отрицательное и по абсолютной величине больше, чем А. Приведем пример.
Десятичная запись Двоичные коды
0 0000011 (прямой код числа 3)
1 1110101 (обратный код числа 10)
1 1111000 (обратный код числа 7)
Получен правильный результат в обратном коде. При переводе в прямой код биты цифровой части результата инвертируются: 1 0000111=-710
Случай 3. А положительное, В отрицательное и по абсолютной величине меньше, чем А. Приведем пример.
Десятичная запись Двоичные коды
0 0001010 (прямой код числа 10)
1 1111100 (обратный код числа 3)
10 0000110 (прямой код числа 6)
Компьютер исправляет полученный первоначально неправильный результат (6 вместо 7) переносом единицы из знакового разряда в младший разряд суммы.
Случай 4. А и В отрицательные. Приведем пример.
Десятичная запись Двоичные коды
1 1111100 (обратный код числа 3)
1 1111000 (обратный код числа 7)
11 1110100 (обратный код числа 11)
При сложении может возникнуть ситуация, когда старшие разряды результата операции не помещаются в отведенной для него области памяти. Такая ситуация называется переполнением разрядной сетки формата числа. Для обнаружения переполнения и оповещения о возникшей ошибке в компьютере используются специальные средства. Ниже приведены два возможных случая переполнения.
Случай 5. А и В положительные, сумма А и В больше либо равна 2n-1, где n – количество разрядов количество разрядов для однобайтового формата n=8, 2n-1=2-7=128). Приведем пример.
Десятичная запись: Двоичные коды:
97 1 0100010 Переполнение
Семи разрядов цифровой части числового формата недостаточно для размещения восьмиразрядной суммы (16210=), поэтому старший разряд суммы оказывается в знаковом разряде. Это вызывает несовпадение знака суммы и знаков слагаемых, что является свидетельством переполнения разрядной сетки.
Случай 6. А и В отрицательные, сумма абсолютных величин А и В больше, либо равна 2n-1. Приведем пример.
Десятичная запись: Двоичные коды:
-158 0 1100000 Переполнение

Здесь знак суммы тоже не совпадает со знаками слагаемых, что свидетельствует о переполнении разрядной сетки.
Все рассмотренные случаи имеют место и при сложении дополнительных кодов чисел.
Случай 1. А и В положительные. Здесь нет отличия от случая 1, рассмотренного для обратного кода.
Случай 2. А положительное, В отрицательное и по абсолютной величине больше, чем А. Приведем пример.
Десятичная запись: Двоичные коды:
Получен правильный результат в дополнительном коде. При переводе в прямой код биты цифровой части результата инвентируются и к младшему разряду прибавляется единица: 1 0000110=-710.
Случай 3. А положительное, В отрицательное и по абсолютной величине меньше, чем А. Приведем пример.
Десятичная запись: Двоичные коды:

Получен правильный результат. Единицу переноса из знакового разряда компьютер отбрасывает.
Случай 4. А и В отрицательные и по абсолютной величине меньше, чем А. Приведем пример.
Десятичная запись: Двоичные коды:

Получен правильный результат в дополнительном коде. Единицу переноса из знакового разряда компьютер отбрасывает.
Случаи переполнения для дополнительных кодов рассматриваются по аналогии со случаями 5 и 6 для обратных кодов.
Сравнение рассмотренных форм кодирования целых чисел со знаком показывает: на преобразование отрицательного числа в обратный код компьютер затрачивает меньше времени, чем на преобразование в дополнительный код, так как последнее состоит из двух шагов – образования обратного кода и прибавления единицы к его младшему разряду; время выполнения сложения для дополнительных кодов чисел меньше, чем для их обратных кодов, потому что в таком сложении нет переноса единицы из знакового разряда в младший разряд результата.
· Умножение и деление. Во многих компьютерах умножение производится как последовательность сложений и сдвигов. Для этого в АЛУ имеется регистр, называемый накапливающим сумматором, который до начала выполнения операции содержит число «нуль».в процессе выполнения операции в нем поочередно размещаются множимое и результаты промежуточных сложений, а по завершении операции – окончательный результат.
Другой регистр АЛУ, участвующий в выполнении этой операции, вначале содержит множитель. Затем по мере выполнения сложений содержащееся в нем число уменьшается, пока не достигнет нулевого значения.
Умножим 1100112 на 1011012.
Пример. Накапливающий сумматор: Множитель:
Сдвиг на две позиции влево
+ Сдвиг на две позиции влево
Деление для компьютера является трудной операцией. Обычно оно реализуется путем многократного прибавления к делимому дополнительного кода делителя.