что такое прямая сумма подпространств

Пересечение и сумма подпространств. Прямая сумма

Пусть дано векторное пространство V, в котором заданы два подпространства U и W.

Определение 1. Пересечением подпространств U и W называется множество UÇW векторов, принадлежащих как подпространству U, так и подпространству W, то есть

Используя теорему 1 § 6, легко проверить, что и сумма, и пересечение подпространств являются подпространствами.

Определение 3. Сумма U+W подпространств U и W называется прямой, если UÇW=<0>.

Прямую сумму подпространств U и V обычно обозначают UÅW.

Теорема 1. Сумма двух подпространств U и W является прямой тогда и только тогда, когда любой вектор z этой суммы единственным образом представим в виде z= x+ y, где xÎU, yÎW.

Достаточность. Пусть представление вектора в виде указанной в теореме суммы единственно. Возьмем любой вектор хÎUÇ W. Тогда хÎU и хÎW, и, заметив, что 0принадлежит любому подпространству, мы можем записать равенство 0 = 0+ 0 = х + (-х), откуда, в силу единственности, следует, что х = 0.

Теорема 2. Размерность суммы двух векторных подпространств равна сумме размерностей этих подпространств без размерности их пересечения, то есть

Если мы докажем, что система (1) линейно независима, то она будет являться базисом суммы подпространств и, следовательно, утверждение теоремы будет доказано. Для этого составим равенство

Перепишем равенство (2) в виде

Из (3) следует, что правая часть этого равенства принадлежит U, так как она выражается через базис подпространства U; вектор в левой части, являясь комбинацией базисных векторов из W, принадлежит W. Но это означает, что и левая, и правая часть равенства (3) является вектором из пересечения UÇW этих подпространств. Поскольку каждый вектор разлагается по базису, разложим левую часть равенства (3) по базису UÇW:

Из (5) мы видим, что линейная комбинация векторов базиса W равна нулю. Следовательно, она тривиальна, в частности, g_m+1=…=g_s=0. Внесем значения этих коэффициентов в равенство (2), тогда получим, что линейная комбинация базисных векторов подпространства U равна нулю и, следовательно, эта комбинация также тривиальна, то есть a₁=…= a_m= b_{m+ 1}= … = b_s= 0. Окончательно имеем, что все коэффициенты в равенстве (2) равны нулю и, следовательно, система (1) линейно независима.

Следствие. dimUÅW = dimU+dimW.

Замечание. Понятие пересечения и суммы подпространств переносятся на любое число подпространств. Так, если даны подпространства U₁,…,U_q, то пересечением их называется множество тех векторов, которые одновременно принадлежат всем рассматриваемым подпространствам, а суммой U₁+…+U_q называется множество всевозможных векторов, представимых в виде x₁+…+x_q, где x₁ÎU₁,…,x_qÎU_q. Если представление вектора суммы в виде x₁+…+x_q единственно, то сумму называют прямой и обозначаютU₁Å…ÅU_q.

Пример. Найти базис и размерность суммы и пересечения подпространств, натянутых на векторы:

А = áа₁,а₂ñ, В = áb₁,b₂ñ

Подпространство A + B состоит из векторов вида a + b, где aÎA, bÎB, следовательно, A + B = áа₁,а₂,b₁,b₂ñ. Составим матрицу из координат указанных векторов и найдем её ранг:

Получаем, ранг равен 3, а потому dim(A+B) = 3. В качестве базиса можно взять систему векторов a₁, a₂, b₁.

Подпространство состоит из всех таких векторов x, что

х = α₁a₁ + α₂a₂ = β₁b₁ + β₂b₂.

1. Какая размерность у линейной оболочки, натянутой на векторы (1,0,0,0), (0,1,0,0), (1,1,0,0), (2,2,0,0)?

2. Сколько различных базисов можно выбрать из системы векторов a, b, cдвумерного векторного пространства,если векторы попарно линейно независимы?

x₁-2x₃+4x₄ +1=0 векторное подпространство в R 4 и если да, то какой размерности?

5.Сколько независимых однородных уравнений входит в систему, определяющую двумерное подпространство пятимерного пространства?

6. Какова размерность векторного пространства всех однородных многочленов от двух переменных степени не выше четырех?

7. Из трех векторов а= (1,1), b =(0,1), c = (1,-1) выбран базис. Указать выбранный базис, если известно, что вектор х= (3,1) имеет в этом базисе координаты 1 и 2.

8. Найти матрицу перехода от базиса е₁ = (1,0), е₂ = (0,1) к базису е₁¢ = (1,2), е₂¢ = (3,4).

9. Пусть R₁[x] – пространство многочленов от одного неизвестного х степени не больше единицы, R 2 – арифметическое двумерное пространство. Изоморфизм j из R 2 в R₁[x] переводит базис е₁ = (1,1) и е₂ = (0,1) соответственно в базис х и 1. Найти образ вектора а= (2,4) при этом изоморфизме.

11. Можно ли векторное пространство размерности не меньше 2 представить в виде прямой суммы двух подпространств?

12. Относительно системы векторов е₁,…,е_n известно следующее: каждый вектор линейно выражается через эту систему, и существует некоторый фиксированный вектор, который единственным образом выражается через эту систему. Будет ли такая система образовывать векторный базис?

13. Образуют ли векторное пространство геометрические векторы на плоскости, не параллельные данной прямой?

14. Доказать, что для любого истинного подпространства U векторного пространства V найдется такое подпространство W, что V=UÅW.

15. Доказать, что пересечение всех подпространств векторного пространства, содержащих два данных подпространства, равно сумме этих двух подпространств.

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.011 сек.)

Источник

Разложение линейного пространства в прямую сумму подпространств

Разложение линейного пространства в прямую сумму подпространств

Последнее уравнение обычно называют пространственным разложением. Людмила Фирмаль

Из всех векторов, параллельных плоскости Окси и подпространству R ^ Все векторы параллельны оси Oz. Теорема 2.10. n-мерное пространство R Прямая сумма подпространств R1 и R2 была достаточной Но пересечение R \ и R ^ содержит только нулевые элементы И так, что размерность R равна сумме субпро-измерений Пространство R \ и R2.

Доказательство. Выберите ei, …, ek в подпункте. Подпространство i пространство R \ и некоторая база gi, …, g / Сочетание этих основ e …, ek, gi, …, g / B.20) Представляет базу всего пространства R. Теорема, размерность n полного пространства R равна сумме k + I R \ а я? В случае 2 теорема 2.5 достаточна для доказательства линейности Независимость элементов Б.20).

Представление B.19) остается доказать уникальным В дополнение к Ним B.19), еще один прогноз настройка х = х; + х2, В.24) Где x ^ — элемент ft, а x2 — элемент ft. Вычтите В.24) из В.19) 0 = xi-x ^ + X2-x2 или xi-x ^ = X2-x2. с того времени Левая часть последнего уравнения — это элемент ft, правая.

Поскольку элемент R2 и пересечение R \ и R2 содержат только нули. Людмила Фирмаль

Элемент, из этого уравнения, xi-x ^ = 0, x2-x2 = 0, То есть х. [= xi, X2 = x2. Теорема доказана. Замечания. Space R Нормальная сумма подпространств R \ и R2, а не напрямую B.19) Пробел R элемент x также действителен, Вообще говоря, это единственный. Например, пусть R трехмерное пространство.

Из всех свободных векторов R \ — подпространство всех векторов, параллельное Плоскость оху, R2 подпространство всех векторов Самолет самолета Oxz. В предыдущем абзаце R Представляет сумму подпрофи (но, конечно, не прямую сумму) Подопечные Ри и R2. i, j, k обозначают базисные векторы.

Разделенные по осям Og, Oy, Oz, любой Существует реальный элемент x пространства R относительно базисов i, j, k Числа a, / 3, 7 — это x = w + /? С другой стороны, потому что J + 7 ^ xi = xi + X2, где xi = w + ^ j — элемент ft, X2 = 7 ^ — элемент С другой стороны, ft — это x = x ^ + x2, а x ^ = ^ j — это элемент ft. x2 = w + 7 ^ это элемент ft

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

ПРЯМАЯ СУММА

— конструкция, широко используемая в теориях таких математич. структур, категории к-рых близки к абелевым категориям;в неабелевом случае конструкция прямой суммы обычно наз. дискретным прямым произведением. Пусть — нек-рый класс однотипных алгебраич. систем, содержащих одноэлементную (нулевую) подсистему. Прямой суммой или (дискретным) прямым произведением систем , из класса U наз. подсиcтема прямого произведения, состоящая из таких функций , все значения к-рых, кроме конечного числа, принадлежат соответствующим нулевым подсистемам. П. с. обозначается одним из следующих способов:

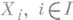
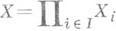
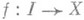
Для конечного числа слагаемых используются также обозначения

Непосредственно из определений следует совпадение П. с. и прямого произведения в случае конечности числа слагаемых.

Для каждого слагаемого П. с. существует канонич. вложение , к-рое элементу сопоставляет функцию , принимающую значение хпри значении аргумента iи равную нулю в остальных случаях. Следовательно, можно считать, что П. с. содержит свои слагаемые. В случае W-групп (в частности, в случае групп, абелевых групп, векторных пространств, колец) можно дать «внутреннее» определение П. с. W-группа G является П. с. своих W-подгрупп , если выполнены следующие условия: a) Gпорождается ; б) каждая W-подгруппа G i является идеалом в G; в) пересечение G i с W-подгруппой, порожденной остальными идеалами, является нулевой подгруппой для каждого i.

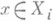
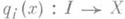
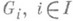
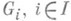
Всякое векторное пространство есть П. с. одномерных подпространств. Всякая свободная абелева группа является П. с. бесконечных циклич. групп. Всякая конечная абелева группа есть П. с. примерных циклич. групп. Всякое ассоциативное кольцо с единицей, удовлетворяющее условию минимальности для идеалов, есть П. с. конечного числа полных колец линейных преобразований подходящих конечномерных векторных пространств.

В теории категории иногда П. с. паз. понятие, двойственное понятию произведения, т. е. копроизведение объектов категории. М. Ш. Цаленко.

Полезное

Смотреть что такое «ПРЯМАЯ СУММА» в других словарях:

Прямая сумма — Символ означает взятие прямой суммы; это также символ Земли в астрономии и астрологии и символ операции исключающее «или». Прямая сумма производный математический объект, создаваемый по определённым ниже правилам из базовых объектов. В качестве… … Википедия

Теория категорий — Теория категорий раздел математики, изучающий свойства отношений между математическими объектами, не зависящие от внутренней структуры объектов. Теория категорий занимает центральное место в современной математике[1], она также нашла… … Википедия

Категория (математика) — Теория категорий раздел математики, изучающий свойства отношений между математическими объектами, не зависящие от внутренней структуры объектов. Некоторые математики[кто?] считают теорию категорий слишком абстрактной и непригодной для… … Википедия

Контравариантный функтор — Теория категорий раздел математики, изучающий свойства отношений между математическими объектами, не зависящие от внутренней структуры объектов. Некоторые математики[кто?] считают теорию категорий слишком абстрактной и непригодной для… … Википедия

Морфизм — Теория категорий раздел математики, изучающий свойства отношений между математическими объектами, не зависящие от внутренней структуры объектов. Некоторые математики[кто?] считают теорию категорий слишком абстрактной и непригодной для… … Википедия

МОДУЛЬ — абелева группа с кольцом операторов. М. является обобщением (линейного) векторного пространства над полем Кдля случая, когда Кзаменяется нек рым кольцом. Пусть задано кольцо А. Аддитивная абелева группа Мназ. левым А модулем, если определено… … Математическая энциклопедия

ЛИ АЛГЕБРА — лиева алгебра, унитарный k модуль Lнад коммутативным кольцом k с единицей, к рый снабжен билинейным отображением прямого произведения в L, обладающим следующими двумя свойствами: 1) [ х, х] = 0 (откуда вытекает антикоммутативность 2) ( х,[ у,… … Математическая энциклопедия

Эллиптическая кривая — Не следует путать с Эллипс. Эллиптическая кривая над полем K это множество точек проективной плоскости над K, удовлетворяющих уравнению вместе с точкой на бесконечности. Эллиптические кривые являются одним из основных объектов изучения в… … Википедия

Источник