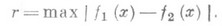что такое пространство в математике
Пространство (математика)
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
В математике (особенно в теории категорий), коммутативная диаграмма — изображаемая в наглядном виде структура наподобие графа, вершинами которой служат объекты определённой категории, а рёбрами — морфизмы. Коммутативность означает, что для любых выбранных начального и конечного объекта для соединяющих их ориентированных путей композиция соответствующих пути морфизмов не будет зависеть от выбора пути.
В математическом анализе, и прилегающих разделах математики, ограниченное множество — множество, которое в определенном смысле имеет конечный размер. Базовым является понятие ограниченности числового множества, которое обобщается на случай произвольного метрического пространства, а также на случай произвольного частично упорядоченного множества. Понятие ограниченности множества не имеет смысла в общих топологических пространствах, без метрики.
О дискретном эквиваленте преобразования Лапласа см. Z-преобразование.В математике дискретный оператор Лапласа — аналог непрерывного оператора Лапласа, определяемого как отношения на графе или дискретной сетке. В случае конечномерного графа (имеющего конечное число вершин и рёбер) дискретный оператор Лапласа имеет более общее название: матрица Лапласа.
В математике особой точкой векторного поля называется точка, в которой векторное поле равно нулю. Особая точка векторного поля является положением равновесия или точкой покоя динамической системы, определяемой данным векторным полем: фазовая траектория с началом в особой точке состоит в точности из этой особой точки, а соответствующая ей интегральная кривая представляет собой прямую, параллельную оси времени.
ПРОСТРАНСТВО
— логически мыслимая форма (или структура), служащая средой, в к-рой осуществляются другие формы и те или иные конструкции. Напр., в элементарной геометрии плоскость или пространство служат средой, где строятся разнообразные фигуры. В большинстве случаев в П. фиксируются отношения, сходные по формальным свойствам с обычными пространственными отношениями (расстояние между точками, равенство фигур и др.), так что о таких П. можно сказать, что они представляют логически мыслимые пространственно-подобные формы. Первым и важнейшим математич. П. является трехмерное евклидово пространство, представляющее приближенный абстрактный образ реального П. Общее понятие «П.» в математике сложилось в результате обобщения и видоизменения понятий геометрии евклидова П. Первые П., отличные от трехмерного евклидова, были введены в 1-й пол. 19 в. Это были Лобачевского пространство и евклидово П. любого числа измерений (см. Многомерная геометрия). Общее понятие о математич. П. как «многократной протяженности» было выдвинуто в 1854 Б. Риманом (В. Riemann); оно обобщалось, уточнялось и конкретизировалось в разных направлениях: таковы, напр., риманово пространство, финслерово пространство, векторное пространство, гильбертово пространство, метрическое пространство, топологическое пространство. В современной математике П. определяют как множество каких-либо объектов, к-рые наз. его точками; ими могут быть геометрич. фигуры, функции, состояния физич. системы и т. д. Рассматривая их множество как П., отвлекаются от всяких их свойств и учитывают только те свойства их совокупности, к-рые определяются принятыми во внимание или введенными по определению отношениями. Эти отношения между точками и теми или иными фигурами, т. е. множествами точек, определяют «геометрию» П. При аксиоматич. ее построении основные свойства этих отношений выражаются в соответствующих аксиомах.
Примерами П. могут служить: 1) метрич. П., в к-рых определено расстояние между точками; напр., П. непрерывных функций на к.-л. отрезке [a, b], где точками служат функции f(x), непрерывные на [ а, b], а расстояние между f 1 (x). и f 2 (x) определяется как максимум модуля их разности:
Полезное
Смотреть что такое «ПРОСТРАНСТВО» в других словарях:
ПРОСТРАНСТВО — фундаментальное (наряду с временем) понятие человеческого мышления, отображающее множественный характер существования мира, его неоднородность. Множество предметов, объектов, данных в человеческом восприятии одновременно, формирует сложный… … Философская энциклопедия
ПРОСТРАНСТВО — П., будучи одним из важнейших элементов мифопоэтической архаичной модели мира, осмысливалось в рамках этой модели совершенно отлично от того, как оно представляется современному человечеству под воздействием научных взглядов (особенно после… … Энциклопедия мифологии
Пространство — Пространство ♦ Espace То, что остается, если убрать все; пустота, но пустота в трех измерениях. Ясно, что понятие пространства – абстракция (если мы действительно уберем все, то не останется вообще ничего, и это будет уже не пространство, а… … Философский словарь Спонвиля
ПРОСТРАНСТВО — в математике множество объектов, между которыми установлены отношения, сходные по своей структуре с обычными пространственными отношениями типа окрестности, расстояния и т. д. Исторически первое и важнейшее математическое пространство евклидово… … Большой Энциклопедический словарь
пространство — См. промежуток. Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. пространство место, промежуток; площадь, участок, зона, район, область; окно, протяженность, прогалина, гаммада,… … Словарь синонимов
пространство — ПРОСТРАНСТВО фундаментальное понятие повседневной жизни и научного знания. Его обычное применение непроблематично в отличие от его теоретической экспликации, поскольку последнее связано с множеством других понятий и предполагает… … Энциклопедия эпистемологии и философии науки
ПРОСТРАНСТВО — ПРОСТРАНСТВО, объективная реальность, форма существования материи, характеризующаяся протяженностью и объемом. В реальном мире мы имеем дело с безграничным трехмерным пространством, в котором расположены объекты. В математике пространством… … Научно-технический энциклопедический словарь
пространство — пространство: восприятие восприятие пространства пространство: восприятие: нарушение … Большая психологическая энциклопедия
ПРОСТРАНСТВО — культуры важнейший аспект модели мира, характеристика протяженности, структурности, сосуществования, взаимодействия, координации элементов отд. культуры и соответствующих отношений между культурами, а также смысловой… … Энциклопедия культурологии
ПРОСТРАНСТВО — ПРОСТРАНСТВО, пространства, ср. 1. Состояние материи, характеризующееся наличием протяженности и объема. Пространство и время основные формы существования материи. 2. Промежуток между чем нибудь; место, способное вместить что нибудь. Свободное… … Толковый словарь Ушакова
Пространство (математика)
В математике слово «пространство» употребляется в большом наборе сложных терминов.
Грубо говоря, пространство есть множество с некоторой дополнительной структурой. В зависимости от этой дополнительной структуры элементы пространства могут называться «точками», «векторами», «событиями» и т. п. Подмножество пространства называется «подпространством», если структура пространства индуцирует на этом подмножестве структуру такого же типа (точное определение зависит от типа пространства).
Примеры
 | Список значений слова или словосочетания со ссылками на соответствующие статьи. Если вы попали сюда из другой статьи Википедии, пожалуйста, вернитесь и уточните ссылку так, чтобы она указывала на статью. |
См. также
Полезное
Смотреть что такое «Пространство (математика)» в других словарях:
ПРОСТРАНСТВО — фундаментальное (наряду с временем) понятие человеческого мышления, отображающее множественный характер существования мира, его неоднородность. Множество предметов, объектов, данных в человеческом восприятии одновременно, формирует сложный… … Философская энциклопедия
МАТЕМАТИКА — наука, или группа наук, о познаваемых разумом многообразиях и структурах, специально – о математических множествах и величинах; напр., элементарная математика – наука о числовых величинах (арифметика) и величинах пространственных (геометрия) и о… … Философская энциклопедия
МАТЕМАТИКА — (греч. mathematike от mathema наука), наука, в которой изучаются пространственные формы и количественные отношения. До нач. 17 в. математика преимущественно наука о числах, скалярных величинах и сравнительно простых геометрических фигурах;… … Большой Энциклопедический словарь
Пространство, время, материя — «ПРОСТРАНСТВО, ВРЕМЯ, МАТЕРИЯ» ставший классическим итоговый труд Г. Вейля по теории относительности (Weyl H. Raum, Zeit, Materie. Verlesungen ueber allgemeine Relativitaetstheorie. Berlin, 1. Aufl. 1918; 5. Aufl. 1923; рус. пер.: Вейль П … Энциклопедия эпистемологии и философии науки
Пространство (физика) — Пространство понятие, используемое (непосредственно или в составе сложных терминов) в естественных языках, а также в таких разделах знания, как философия, математика, физика и т. п. На уровне повседневного восприятия пространство интуитивно… … Википедия
Математика — Евклид. Деталь «Афинской школы» Рафаэля Математика (от др. греч … Википедия
Математика Древнего Востока — История науки По тематике Математика Естественные науки … Википедия
Математика — I. Определение предмета математики, связь с другими науками и техникой. Математика (греч. mathematike, от máthema знание, наука), наука о количественных отношениях и пространственных формах действительного мира. «Чистая … Большая советская энциклопедия
Что такое пространство в математике
Рассказывать школьникам о пространстве не как философской категории, а как о математическом понятии очень непросто. Об этом почти нет популярной литературы, а имеющиеся учебники адресованы студентам математических факультетов университетов. Я предлагаю свой рассказ о том, что такое пространство в математике.
Наверное, нужно начать с того, что пространство — очень объемное понятие, которому в разных контекстах придаются самые различные смыслы: вспомним хотя бы космическое, воздушное, межклеточное или информационное пространство. Конечно, разумно было бы начать с определения, однако пространство, как и любое другое основное понятие, является неопределяемым (аналогично число, множество, функция в алгебре, точка, прямая, плоскость в геометрии). Неопределяемые понятия мы можем только описывать, разъясняя, что имеется в виду, заменяя определяемое слово синонимами, обращаясь к интуиции и жизненному опыту.
Итак, под пространством понимают множество некоторых объектов, правила работы с ними и набор аксиом, которым эти правила должны подчиняться. Иными словами, это множество со введенной на нем структурой. По-разному определяя множество и структуру, мы получаем разные пространства. Из изучаемых школьном курсе можно отметить Евклидово пространство (одномерное, двумерное и трехмерное), линейное или векторное пространство и вероятностное пространство. Их элементами являются соответственно точки, векторы и элементарные события. Упоминается также четырехмерное пространство-время — пространство Минковского. (Заметим, что пространство Минковского не является четырехмерным Евклидовым пространством, поскольку имеет три пространственные и одну временную, но не пространственную, координату).
Одной из важнейших характеристик пространства является его размерность. С точки зрения аналитической геометрии, размерность фигуры равна числу координат, нужных для определения положения лежащей на этой фигуре точки; например, положение точки на кривой определяется одной координатой, на поверхности — двумя координатами, в трёхмерном пространстве — тремя координатами. (Необходимо отметить, что с середины 19 века геометрия стала изучать многомерные пространства, а в 20 веке — и пространства дробных размерностей).
Примером одномерного пространства является числовая прямая, положение каждой точки на ней можно характеризовать единственным числом. На прямой могут располагаться точки и отрезки (интервалы, полуинтервалы), они имеют одну пространственную характеристику — протяженность или длину. Примером двумерного пространства является плоскость, точки плоскости задаются двумя координатами. Плоские объекты характеризуются не только длиной, но и шириной. Примером трехмерного пространства является окружающий нас мир (Это утверждение верно до некоторых пределов. С точки зрения общей теории относительности, наш мир — искривляемое массивными телами четырехмерное пространство-время). Наряду с длиной и шириной появляется третье измерение, называемое высотой. Положение точек в трехмерном пространстве задается тремя пространственными координатами, в прямоугольной системе координат называемыми абсциссой, ординатой и аппликатой.
В рамках базовой школьной программы изучается только прямоугольная система координат. Однако необходимо отметить, что существуют и непрямоугольные системы координат, например, полярная и сферическая. В полярной системе координат на плоскости положение точки характеризуется двумя числами: расстоянием от точки до полюса и углом между полярной осью и отрезком, соединяющим точку с полюсом. Эта система координат удобна тем, что в ней уравнения некоторых линий принимают более простой вид, чем в прямоугольной системе координат. Аналогично, для задания положения точки на поверхности Земного шара понятия широты и долготы более удобны, чем какие-либо другие координаты. В сферической системе координат положение точки задают расстоянием от нее до начала координат, зенитным и азимутальным углами.
В физике используется «фазовая плоскость» — координатная плоскость, в которой по осям координат откладываются какие- либо две переменные (фазовые координаты), однозначно определяющие состояние системы. Каждому возможному состоянию системы соответствует точка фазового пространства. Изменение состояния системы отображается на фазовой плоскости движением этой точки. Фазовая плоскость является частным случаем фазового пространства, которое может иметь большую размерность. Состояние сколь угодно сложной системы представляется в фазовом пространстве одной единственной точкой, а эволюция этой системы — перемещением этой точки.
Конечно, наибольший интерес вызывает обсуждение многомерных гипертел. Приведем схему, позволяющую представить эволюцию геометрических объектов от точки до четырехмерного гиперкуба. Пусть у нас есть точка, которую мы сдвигаем вдоль прямой на некоторое расстояние. Если мы представим, что при движении точка оставляет след, то в результате сдвига мы получим отрезок. Будем теперь смещать отрезок в перпендикулярном ему направлении на расстояние, равное его длине. Результат построения — квадрат. Смещая теперь квадрат в перпендикулярном его плоскости направлению на расстояние, равное длине его стороны, получим куб. Рассуждая аналогично, мы можем вообразить четырехмерный гиперкуб. Он будет результатом смещения нашего трехмерного куба в направлении ему перпендикулярном на расстояние, равное длине любого из его ребер (см. рис. 1).
Больше того, наш алгоритм позволяет заметить геометрические характеристики гиперкуба! Проследим поэтапно: начальное и конечное положение движущейся точки обусловили наличие двух вершин отрезка. В свою очередь, четыре вершины квадрата образовались из двух вершин исходного и еще двух — смещенного отрезка. Число вершин куба представляет собой сумму числа вершин исходного и смещенного квадратов, поэтому их восемь, а число вершин гиперкуба будет равно шестнадцати — это вершины исходного и смещенного кубов. (Заметим, что число вершин 2, 4, 8, 16… является геометрической прогрессией.)
Продолжим наши наблюдения за объектом, который мы не в силах представить, но можем охарактеризовать. Единственная «сторона» отрезка — результат движения точки. Четыре стороны квадрата складываются из начального и конечного отрезков и еще двух отрезков, соединяющих исходные, и полученные смещением вершины этого отрезка. Поэтому же число ребер куба равно 12 (это по 4 стороны исходного и смещенного квадратов и еще 4 ребра, соединяющие соответствующие вершины исходного и смещенного). Аналогично число ребер гиперкуба — 32 (это по 12 ребер исходного и смещенного кубов и еще 8 ребер, образованных при движении 8 вершин исходного куба).
Далее, у нашего трехмерного куба 6 плоских граней — это исходный и смещенный квадраты, а также квадраты, полученные движением 4 сторон исходного квадрата. Аналогично число плоских граней гиперкуба — 24: по 6 граней у исходный и смещенного кубов, и еще 12, полученных движением 12 ребер исходного куба. Помимо 24 плоских граней, гиперкуб будет иметь еще 8 кубических граней: действительно, отрезок ограничен 2 точками, квадрат — 4 сторонами, куб — 6 гранями, гиперкуб — 8 кубами и т. д.; числа 2, 4, 6, 8… образуют арифметическую прогрессию. (Продолжая, мы можем рассматривать пятимерный гиперкуб. Он имеет 32 вершины, 80 ребер, 80 квадратных, 40 кубических и 10 гиперкубических граней. И так далее.)
При всей схожести построения объектов, пространства, в которых они существуют совсем разные.
Рассмотрим мир жителей прямой. Вне прямой для них ничего не существует, просто ничего нет, даже пустоты. Внутри этого мира органами зрения можно видеть лишь точки. Это сами точки, или перпендикулярные проекции отрезков (представьте, что мы смотрим на иголку со стороны острия). Движение возможно только между двумя объектами на прямой, так как обойти точки, не сходя с этой нее, невозможно (см. рис. 2).
Двумерный мир представляет собой плоскость. Обитатели этого мира — точки, отрезки, плоские фигуры. Глядя друг на друга, они могут видеть лишь отрезки, которыми являются проекции плоских фигур на прямую (см. рис. 3).
Трехмерный мир окружает нас. Мы привыкли к нему, объекты, окружающие нас трехмерны, хоть в каждый момент времени мы видим только их плоские проекции — как на фотографии. Если бы мы были четырехмерными, в трехмерном мире перед нами открылись самые фантастические возможности.
Например, рассматривая плоский мир рисунка (см. [3], стр. 101), мы видим внутренность всех комнат, равно как и их обитателей и всего дома (см. рис. 4). Аналогично мы увидели бы улицы, горы и пещеры, извилистые лабиринты и спрятанные тайники, небеса и подземелья — все открывается взгляду и видно насквозь. Один из героев книги — Сфера — является перед жителем плоского мира Флатландии и пытается доказать ему существование неизвестного тому третьего измерения. Для убедительности со словами «… легкая боль, которую вы, быть может, ощутите, не идет ни в какое сравнение с выгодой, извлекаемой из этого прикосновения вашим умом», трехмерная Сфера даже касается желудка двумерного квадрата» [3, стр. 98].
Итак, из следующего измерения мы получаем возможность видеть насквозь все, происходящее в пространстве меньшей размерности, возможность беспрепятственно перемещать предметы сквозь границы, видоизменяться в пространствах меньшей размерности, появляясь в них тем или иным своим многомерным сечением, исчезать в одной точке и появляться в другой точке беспричинно и непредсказуемо для обитателей меньших размерностей. В этом, несмотря на всю непохожесть, наши пространства имеют много общего.
Сила и красота математики, ее абстрактность и универсальность состоят как раз в том, что она находит универсальные единые методы описания пространств, что используемый язык позволяет строить плодотворные модели и аналогии для самых непохожих на первый взгляд объектов.
[3] Эбботт Э. Э. Флатландия, Бюргей Д. Сферландия. — М., «Мир», 1976.
ПРОСТРАНСТВО
— логически мыслимая форма (или структура), служащая средой, в к-рой осуществляются другие формы и те или иные конструкции. Напр., в элементарной геометрии плоскость или пространство служат средой, где строятся разнообразные фигуры. В большинстве случаев в П. фиксируются отношения, сходные по формальным свойствам с обычными пространственными отношениями (расстояние между точками, равенство фигур и др.), так что о таких П. можно сказать, что они представляют логически мыслимые пространственно-подобные формы. Первым и важнейшим математич.П. является трехмерное евклидово пространство, представляющее приближенный абстрактный образ реального П. Общее понятие «П.» в математике сложилось в результате обобщения и видоизменения понятий геометрии евклидова П. Первые П., отличные от трехмерного евклидова, были введены в 1-й пол. 19 в. Это были Лобачевского пространство и евклидово П. любого числа измерений (см. Многомерная геометрия). Общее понятие о математич. П. как «многократной протяженности» было выдвинуто в 1854 Б. Риманом (В. Riemann); оно обобщалось, уточнялось и конкретизировалось в разных направлениях: таковы, напр., риманово пространство, финслерово пространство, векторное пространство, гильбертово пространство, метрическое пространство, топологическое пространство. В современной математике П. определяют как множество каких-либо объектов, к-рые наз. его точками; ими могут быть геометрич. фигуры, функции, состояния физич. системы и т. д. Рассматривая их множество как П., отвлекаются от всяких их свойств и учитывают только те свойства их совокупности, к-рые определяются принятыми во внимание или введенными по определению отношениями. Эти отношения между точками и теми или иными фигурами, т. е. множествами точек, определяют «геометрию» П. При аксиоматич. ее построении основные свойства этих отношений выражаются в соответствующих аксиомах.
Примерами П. могут служить: 1) метрич. П., в к-рых определено расстояние между точками; напр., П. непрерывных функций на к.-л. отрезке [a, b], где точками служат функции f(x), непрерывные на [ а, b], а расстояние между f1(x). и f2(x) определяется как максимум модуля их разности:
Смотреть что такое ПРОСТРАНСТВО в других словарях:
ПРОСТРАНСТВО
(филос.). — Для правильного объяснения П. необходимо, прежде всего, отчетливо различить в нем чистый факт — то, что дано в самом существовании П. как т. смотреть
ПРОСТРАНСТВО
в математике, логически мыслимая форма (или структура), служащая средой, в которой осуществляются другие формы и те или иные конструкции. Напри. смотреть
ПРОСТРАНСТВО
ПРОСТРАНСТВО
ПРОСТРАНСТВО
ПРОСТРАНСТВО
ПРОСТРАНСТВО
ПРОСТРАНСТВО
Пространство (филос.). — Для правильного объяснения П. необходимо, прежде всего, отчетливо различить в нем чистый факт — то, что дано в самом существовании П. как такового и не может подлежать сомнению, — от тех суждений об этом факте, которые выражают его гносеологическую и метафизическую оценку. I. Самый факт П., или то, что в нем дается, заключает, несомненно, две стороны; первая состоит в известном образе или представлении протяженности (зрительно-осязательном для зрячих, только осязательном для слепорожденных), причем этот образ, сохраняя свое единство в целом, разлагается по частям в нашем воззрении на определенные измеримые очертания и расстояния внешних предметов как тел геометрических. От этой формальной или геометрической стороны П. ipso facto различается реальная или механическая его сторона, состоящая в вещественной раздельности или разъединенности («внебытии») всего существующего, в силу которой для реального сближения и теснейшего взаимодействия или соотношения двух отдаленных в П. существ необходимо употребить определенное количество внутренних усилий и внешних движений, прямых и косвенных, единичных и собирательных, в зависимости от данного расстояния и других механических условий. Если бы, находясь, например, в Петербурге и желая пожать руку приятелю в Квебеке, мы всегда могли сразу очутиться около него безо всяких усилий и сложных передвижений, то, конечно, мы не могли бы сознавать себя подчиненными пространственным ограничениям, хотя бы при этом весь наш мир не менее теперешнего был наполнен протяженными образами различных предметов с определенными геометрическими расстояниями между ними: при отсутствии тяготеющей над нами внешней необходимости преодолевать механически нашу разъединенность с другими, мы чувствовали бы не себя в П., а П. в себе, — подобно тому, как в сновидениях, субъект их свободен от границ П., хотя все грезящиеся образы имеют такую же форму определенной протяженности, как и наяву. Когда мы видим во сне башню на высокой горе или женщину с младенцем на руках, то младенец меньше женщины и башня меньше горы, а если бы вслед за тем мы и увидели младенца величиной с мамонта, или башню доходящую до неба, то это были бы уже другие образы; точно так же и наяву предметы воображаемые выступают под формой протяженности со всеми ее определенными отношениями очертаний, величины и расстояния. И если, однако, ни протяженные образы сонных грез, ни протяженные представления фантазии, не выражая никакой внешней необходимости, поэтому и не входят в состав реально-определенного и ограничивающего нас П., то ясно, что сущность последнего состоит не в форме протяженности, а именно лишь в необходимости механических усилий для целесообразного действия в нашей вещественной среде. Будучи выражением рокового разъединения и отчуждения между всеми частями существующего, реальное П., вместе с тем, как нечто общее для всех, постоянное и одинаково необходимое, есть внешнее условие общения и относительного соединения. В обычных сновидениях, когда жизнь индивидуальной души временно отрешается от трудового стремления к реализации в общих принудительных пределах действительного П., у каждого субъекта оказывается свой особый мир, совершенно разобщенный с другими, и субъективная свобода от «оков П. » допускает лишь обманчивую легкость сближения и общения с призраками других субъектов. Итак, реальное П. фактически есть постоянный показатель действительного разъединения и, вместе с тем, необходимое условие для действительного соединения данных в нашем мире существ. Та сторона существ, которой они подлежат такому внешнему разъединению и соединению, называется физическим телом, и самое простое выражение для факта реального П. дается аксиомой непроницаемости: два тела не могут совместно занимать одну и ту же часть П. II. Что касается до теоретического толкования реального факта, то оно менялось сообразно различным точкам зрения, выступавшим в истории философии, причем несогласие между различными теориями П. происходило отчасти от недостаточно ясного разграничения между реально-механическим и формально-геометрическим элементами П.; т. е. между фактом телесной непроницаемости и представлением протяженности с ее измеряемыми образами. В древней философии взгляд на П. самый простой и близкий к наивному (нефилософскому) сознанию представляется атомистикой Левкиппа и Демокрита, видевших в П. пустоту (τό κενον), в которой движутся реальные единицы, образующие все существующее. Для Платона, как можно заключать из диалога Тимей, П. (χωρα) отожествлялось с тем несуществующим (μη όν), в котором он видел материю чувственно-являемого мира: в сущности это сводилось к тому же представлению пустоты или реального ничто. Аристотель отрицает этот взгляд, но не ставит на его место никакого собственного. Настоящего философского объяснения П. мы у него не находим: его определение места (τόπος), как границы объемлющего тела по отношению к объемлемому, есть только вербальное; с другой стороны, понятие где (ποΰ) называется им как одна из 10 категорий; вообще, Аристотель, в противоположность атомистам и Платону, интересовался, по-видимому, только формальной стороной П. — односторонность, завещанная им и средневековой схоластике. В новой философии Декарт, приписывая П. особую, независимую от нашего духа, или несводимую к нашему мышлению реальность, но отрицая атомистическое понятие пустоты, понимал П. как непрерывную или сплошную протяженность; единственным основным качеством тел, как таковых, он признавал протяжение, сводя, таким образом, реальную сторону П. к формальной, причем различие тела геометрического от физического не имело принципиального объяснения. Такое объяснение, хотя и не вполне удовлетворительное, получается с точки зрения Спинозы. Хотя и он отожествляет П. с протяжением, но, признавая последнее атрибутом единой абсолютной субстанции наряду с мышлением, он может дать отчет в реальной независимости П. от мыслящего субъекта, — независимости вполне признанной, но ничем философски не обоснованной у Декарта; для Спинозы она обосновывается равноправностью двух атрибутов. С этой точки зрения понятно различие между телом отвлеченно-мыслимым или геометрическим и телом действительно существующим или данным в опыте (тело физическое): первое, как мысль, есть модус (видоизменение) мышления, формально связанный, но не тожественный реально с соответствующим модусом протяжения, тогда как тело физическое есть модус именно протяжения, другого божественного атрибута, не находящегося ни в какой прямой зависимости от мысли, как таковой — отсюда реальность и необходимость внешних вещей для нас. Хотя в этом грандиозном взгляде дано некоторое общепринципиальное основание для различения тела геометрического, мыслимого, или идеально-протяженного, от тела физического, ощущаемого, или реально-протяженного, но, как и во всем картезианстве, остается необъяснимым познавательное и практическое взаимодействие между мыслящим субъектом и физической телесностью его собственной и посторонней. Ясно, что это взаимодействие не дано ни в атрибуте мышления, ни в атрибуте протяжения, а должно бы происходить в какой-то посредствующей области, недоступной с этой точки зрения (см. Спиноза). По воззрениям Лейбница, которым он сам не дал, к сожалению, полного и последовательного выражения, и которые получили от Вольфа и его школы лишь формальную и поверхностную систематизацию, мир есть совокупность психических единиц (монад), находящихся на различных степенях внутреннего развития, причем П. понимается как порядок существования всего данного или являемого в смутном чувственном восприятии недоразвившихся монад; но так как реального взаимодействия между монадами Лейбниц не допускает, то непреклонное единство пространственной среды для всех монад нашего мира совершенно независимо от степени их развития, остается невыясненным и название Лейбницем видимого мира phaenomenon bene fundat u m не имеет в этой философии достаточного оправдания. Факт достоверного познания пространственных отношений как всеобщих и необходимых объясняется в «трансцендентальной эстетике» Канта через признание П. априорной формой нашего чувственного воззрения, как такового. П. (со всеми геометрическими определениями и отношениями) не воспринимается извне, а налагается познающим субъектом, как присущий ему способ представления, на весь материал чувственных восприятий или ощущений так называемых внешних чувств. Это учение об идеальности или, точнее, — субъективности П., как основной формы представления, — совершенно верное в том, что оно утверждает положительно, ибо, несомненно, что созерцаемые пространственные отношения не могут как созерцаемые существовать вне созерцающего субъекта, — вызывает, однако, новые вопросы, не находящие себе удовлетворительного решения в философии Канта. Когда говорится, что П. есть форма, a priori присущая нашему чувственному воззрению, то что собственно разумеется под словом «нашему»? Если имеется в виду субъект эмпирический, т. е. каждый из множества чувственно-воспринимающих особей, то необъясненными остаются: 1) действительное единство или взаимность пространственных отношений — познавательных и двигательных (геометрических и механических) между всеми, — как человеческими, так и животными, — субъектами, ибо такое единство не вытекает из формальной общности П. как априорного способа воззрения, так как эта общность или одинаковость пространственной формы сохраняется, например, и в сновидениях, причем, однако, каждый грезящий субъект остается, пока грезит, при своем особом воображаемом П. вне всякой связи с другими; то различие между «грезящим» идеализмом и истинным «трансцендентальным», на котором так решительно и, разумеется, искренне настаивает Кант, не имело бы никакого принципиального основания, если субъектом П. (и прочих априорных форм и условий познания) признать субъект эмпирический, т. е. данную множественность познающих органических особей. 2) Несомненно, что самое возникновение эмпирических субъектов дано в мире явлений под формой П. (времени и т. д.) и, следовательно, всякий эмпирический субъект предполагает уже эти априорные формы и условия являемого бытия, и никакой эмпирический субъект не может быть их первоначальным носителем. 3) Если с одной стороны в определении П. как априорной формы воззрения, присущей нашему субъекту, не заключается оснований для данного в опыте действительного общения всех субъектов в одном П., то, вместе с тем, не дано никакого объяснения и для роковых границ, полагаемых этому общению тем же единым П. — в факте тяготеющей над всеми эмпирическими субъектами необходимости практических усилий для преодоления реальных расстояний, что ни в какой логический связи с П., как чистой формой воззрения, не находится, и, однако же, составляет неустранимый признак действительного П., отличающий его от П. грез. Но если таким образом П., будучи априорной формой воззрения субъекта, вместе с тем несомненно предполагается самым существованием эмпирических субъектов и притом имеет над ними принудительную силу, определяющую условия их чувственного общения и разобщения, то ясно, что субъект, которым первоначально полагается эта форма воззрения, не совпадает с множественностью эмпирических субъектов, а есть единый и относительно их объективно-необходимый, самостоятельный трансцендентальный субъект. Итак, вопрос о П. по существу допускает лишь чисто метафизическое решение (см. Философия). Лишь кажущееся отношение к этому вопросу имеет другой — о психофизических условиях образования пространственных восприятий и представлений, где дело идет об известных процессах приспособления нервной и мускульной системы данных организмов к явлениям внешней среды — что, очевидно, может происходить лишь под условием уже существующего П., как общей формы явлений (см. Психофизиология). Поэтому принимать эти эмпирические исследования и гипотезы за философские объяснения самого П. было бы грубой логической ошибкой. См. в особенности Job. Jul. Baumann, «Die Lehren von Raum in der neueren Philosophie» (Берлин, 1868—69). Вл. С.
ПРОСТРАНСТВО
ПРОСТРАНСТВО — фундаментальное (наряду с временем) понятие человеческого мышления, отображающее множественный характер существования мира, его неод. смотреть
ПРОСТРАНСТВО
ПРОСТРАНСТВО культуры важнейший аспект модели мира, характеристика протяженности, структурности, сосуществования, взаимодействия, ко. смотреть
ПРОСТРАНСТВО
ПРОСТРАНСТВО — фундаментальное понятие повседневной жизни и научного знания. Его обычное применение непроблематично в отличие от его теоретичес. смотреть
ПРОСТРАНСТВО
ПРОСТРАНСТВО
ПРОСТРАНСТВОП., будучи одним из важнейших элементов мифопоэтической архаичной модели мира, осмысливалось в рамках этой модели совершенно отлично от тог. смотреть