что такое проекция в геометрии 8 класс в прямоугольном треугольнике
Прямоугольный треугольник
Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).
Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.
Признаки равенства прямоугольных треугольников
Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).
Свойства прямоугольного треугольника
1. Сумма острых углов прямоугольного треугольника равна 90˚.
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.
И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.
3. Теорема Пифагора:
, где
– катеты,
– гипотенуза. Видеодоказательство
4. Площадь прямоугольного треугольника с катетами
:
5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты
и гипотенузу
следующим образом:
6. Центр описанной окружности – есть середина гипотенузы.
7. Радиус описанной окружности есть половина гипотенузы
:
8. Медиана, проведенная к гипотенузе, равна ее половине
9. Радиус вписанной окружности выражается через катеты
и гипотенузу
следующим образом:
Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.
Что такое проекция в геометрии 8 класс в прямоугольном треугольнике
Основные метрические сооьтношения в прямоугольном треугольнике
§1. Прямоугольный треугольник. Метрические соотношения.
Основные метрические сооьтношения в прямоугольном треугольнике
Пусть `ABC` прямоугольный треугольник с прямым углом `C` и острым углом при вершине `A`, равным `alpha` (рис. 1).
Используем обычные обозначения:
`a_c` и `b_c` – проекции `BD` и `AD` катетов на гипотенузу;
`h` – высота `CD`, опущенная на гипотенузу;
`m_c` – медиана `CM`, проведённая к гипотенузе;
`R` – радиус описанной окружности;
`r` – радиус вписанной окружности.
`sin alpha = a/c`, `cos alpha = b/c` и `»tg»alpha = a/b`.
Значения синуса, косинуса и тангенса острого угла прямоугольного треугольника зависят только от меры угла и не зависят от размеров и расположения треугольника.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
`c^2 = a^2 + b^2`
Доказательство теоремы повторите по учебнику.
Выведем ряд соотношений между элементами прямоугольного треугольника.
Квадрат катета равен произведению гипотенузы и его проекции на гипотенузу
Квадрат высоты, опущенной на гипотенузу, равен произведению проекции катетов на гипотенузу
Из треугольника `ACD` (рис. 1) имеем `»tg»alpha = (CD)/(AD)`, а из треугольника `BCD` `»tg»alpha = (BD)/(CD)`.
Значит `(BD)/(CD) = (CD)/(AD)`, откуда `CD^2 = AD * BD`, т. е. `h^2 = a_c * b_c`.
Произведение катетов равно произведению гипотенузы и высоты, опущенной на гипотенузу
Из треугольника `ABC` имеем `sin alpha = (BC)/(AB)`, а из треуольника `ACD` `sin alpha = (CD)/(AC)`.
Таким образом, `(BC)/(AB) = (CD)/(AC)`, откуда `BC * AC = AB * CD`, т. е. `a * b = c * h`.
Медиана, проведённая к гипотенузе, равна половине гипотенузы, т. е.
.
Полезно также запомнить, что медиана к гипотенузе разбивает треугольник на два равнобедренных треугольника.
Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы
Это следует из Свойства 4, действительно, `MA = MB = MC`, следовательно, окружность с центром в точке `M` и радиуса `c/2` проходит через три вершины.
Сумма катетов равна удвоенной сумме радиусов описанной и вписанной окружностей
`a + b = 2(R + r)` или `a + b = c + 2r`
Равенства, доказанные в Свойствах 1 и 2, записываются также как:
Что такое проекция в геометрии 8 класс в прямоугольном треугольнике
§ 16. Теорема Пифагора.
§ 17. Тригонометрические функции острого угла прямоугольного треугольника.
§ 18. Решение прямоугольных треугольников.
ИТОГИ ГЛАВЫ 3
Метрические соотношения в прямоугольном треугольнике
Квадрат высоты прямоугольного треугольника, проведённой к гипотенузе, равен произведению проекций катетов на гипотенузу. Квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу.
Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Синус острого угла прямоугольного треугольника
Синусом острого угла прямоугольного треугольника называют отношение противолежащего катета к гипотенузе.
Косинус острого угла прямоугольного треугольника
Косинусом острого угла прямоугольного треугольника называют отношение прилежащего катета к гипотенузе.
Тангенс острого угла прямоугольного треугольника
Тангенсом острого угла прямоугольного треугольника называют отношение противолежащего катета к прилежащему.
Котангенс острого угла прямоугольного треугольника
Котангенсом острого угла прямоугольного треугольника называют отношение прилежащего катета к противолежащему.
Тригонометрические формулы
Соотношения между сторонами и значениями тригонометрических функций углов в прямоугольном треугольнике
«Мерзляк Геометрия 8 Глава 3» СОДЕРЖАНИЕ: § 15. Метрические соотношения в прямоугольном треугольнике. § 16. Теорема Пифагора. § 17. Тригонометрические функции острого угла прямоугольного треугольника. § 18. Решение прямоугольных треугольников.
Это конспект по теме «Мерзляк Геометрия 8 Глава 3». Выберите дальнейшие действия: Вернуться к Списку конспектов по геометрии.
Узнать ещё
Знание — сила. Познавательная информация
Пропорциональные отрезки в прямоугольном треугольнике
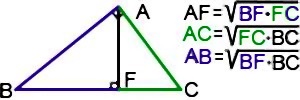
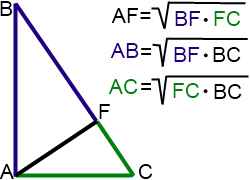
Запомнить соотношения, связывающие пропорциональные отрезки в прямоугольном треугольнике, помогает цветовая ассоциация.
Высота прямоугольного треугольника, проведенная к гипотенузе, делит ее на отрезки, которые называются проекциями катетов на гипотенузу.
Свойства прямоугольного треугольника:
1. Высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу.
2. Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.
Например, в треугольнике ABC AF — высота, проведенная к гипотенузе BC, BF — проекция катета AB на гипотенузу, FC — проекция катета AC на гипотенузу.
Если выделить каждую пару — катет и его проекция на гипотенузу — одним цветом, запомнить пропорциональные отрезки в прямоугольном треугольнике можно быстро и легко.
Как бы ни был расположен на чертеже прямоугольный треугольник, цветовая ассоциация поможет найти пропорциональные отрезки и правильно составить связывающие их соотношения:
Выделить пропорциональные отрезки цветами можно на черновике. При решении задачи, в которой прямоугольный треугольник — только один из элементов чертежа, достаточно для нахождения связи между пропорциональными отрезками на черновике изобразить отдельный фрагмент с этим треугольником.
Прямоугольные треугольники
Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
Значения тригонометрических функций некоторых углов:
Площадь прямоугольного треугольника равна половине произведения его катетов
Подставим найденное значение в формулу косинуса
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.
В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.
Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.