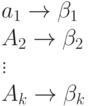что такое префиксный код
Кодирование информации
| Определение: |
| Кодирование информации (англ. information coding) — отображение данных на кодовые слова. |
Обычно в процессе кодирования информация преобразуется из формы, удобной для непосредственного использования, в форму, удобную для передачи, хранения или автоматической обработки. В более узком смысле кодированием информации называют представление информации в виде кода. Средством кодирования служит таблица соответствия знаковых систем, которая устанавливает взаимно однозначное соответствие между знаками или группами знаков двух различных знаковых систем.
Содержание
Код [ править ]
Виды кодов [ править ]
Все вышеперечисленные коды являются однозначно декодируемыми — для такого кода любое слово, составленное из кодовых слов, можно декодировать только единственным способом.
Примеры кодов [ править ]
Однозначно декодируемый код [ править ]
| Определение: |
| Однозначно декодируемый код (англ. uniquely decodable code) — код, в котором любое слово составленное из кодовых слов можно декодировать только единственным способом. |
Пусть есть код заданный следующей кодовой таблицей:
[math]a_1 \rightarrow b_1[/math]
[math]a_2 \rightarrow b_2[/math]
[math]a_k \rightarrow b_k[/math]
Код является однозначно декодируемым, только тогда, когда для любых строк, составленных из кодовых слов, вида:
Всегда выполняются равенства:
Заметим, что если среди кодовых слов будут одинаковые, то однозначно декодировать этот код мы уже не сможем.
Префиксный код [ править ]
| Определение: |
| Префиксный код (англ. prefix code) — код, в котором никакое кодовое слово не является префиксом какого-то другого кодового слова. |
Предпочтение префиксным кодам отдается из-за того, что они упрощают декодирование. Поскольку никакое кодовое слово не выступает в роли префикса другого, кодовое слово, с которого начинается файл, определяется однозначно, как и все последующие кодовые слова.
Пример кодирования [ править ]
Закодируем строку [math]abacaba[/math] :
Такой код можно однозначно разбить на слова:
[math]00\ 01\ 00\ 1\ 00\ 01\ 00[/math]
Преимущества префиксных кодов [ править ]
Недостатки префиксных кодов [ править ]
Пример неудачного декодирования [ править ]
Предположим, что последовательность [math]abacaba[/math] из примера передалась неверно и стала:
[math]c^<**>(abacaba) = 0001001\ 1\ 00100[/math]
Разобьем ее согласно словарю:
[math] 00\ 01\ 00\ 1\ 1\ 00\ 1\ 00[/math]
[math]a\quad b\quad a\ c\ c\quad a\ c\ a[/math]
Полученная строка совпадает только в битах, которые находились до ошибочного, поэтому декодирование неравномерного кода, содержащего ошибки, может дать абсолютно неверные результаты.
Не префиксный однозначно декодируемый код [ править ]
Как уже было сказано, префиксный код всегда однозначно декодируем. Обратное в общем случае неверно:
Мы можем ее однозначно декодировать, так как знаем, что слева от двойки и справа от тройки всегда стоит единица.
После декодирования получаем: [math]abbca[/math]
Префиксный код
Пре́фиксный код в теории кодирования — код со словом переменной длины, имеющий такое свойство (выполнение условия Фано): если в код входит слово a, то для любой непустой строки b слова ab в коде не существует. Хотя префиксный код состоит из слов разной длины, эти слова можно записывать без разделительного символа.
Например, код, состоящий из слов 0, 10 и 11, является префиксным, и сообщение 01001101110 можно разбить на слова единственным образом:
Код, состоящий из слов 0, 10, 11 и 100, префиксным не является, и то же сообщение можно трактовать несколькими способами.
Определение
Так называемые «префиксы» могут быть получены путём последовательного отбрасывания последнего знака кодовой комбинации. Например, для кодовой комбинации 11101101 префиксами будут 11101101, 1110110, 111011, 11101, 1110, 111, 11, 1.
Если промежутков или других знаков препинания между кодовыми комбинациями нет, то для однозначного декодирования комбинации 111011101 ни одна из кодовых комбинаций не может быть представлена перечисленными вариантами (префиксами). Код называется префиксным, если ни одна из его комбинаций не является префиксом другой комбинации того же кода. Часть кодовой комбинации, которая дополняет префикс до самой комбинации, называется суффиксом. Префиксные коды наглядно могут быть представлены с помощью кодовых деревьев. Если ни один узел кодового дерева не является вершиной данного кода, то он обладает свойствами префикса. Узлы дерева, которые не соединяются с другими, называются конечными. Комбинации, которые им соответствуют, являются кодовыми комбинациями префиксного кода.
Примеры
Любой код со словом фиксированной длины, очевидно, является префиксным. Рассмотрим несколько нетривиальных примеров.
Код Морзе не является префиксным. В него, кроме точки и тире, входит также символ-разделитель — пауза длиной в тире.
См. также
 | Это заготовка статьи о компьютерах. Вы можете помочь проекту, исправив и дополнив её. Это примечание по возможности следует заменить более точным. |
Полезное
Смотреть что такое «Префиксный код» в других словарях:
префиксный код — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN prefix code … Справочник технического переводчика
код Хаффмана — Префиксный код, в котором длина кодирующего слова обратно пропорциональна встречаемости кодируемого элемента. [Е.С.Алексеев, А.А.Мячев. Англо русский толковый словарь по системотехнике ЭВМ. Москва 1993] Тематики информационные технологии в целом… … Справочник технического переводчика
Код — У этого термина существуют и другие значения, см. Код (значения). Код правило (алгоритм) сопоставления каждому конкретному сообщению строго определённой комбинации символов (знаков) (или сигналов). Кодом также называется отдельная… … Википедия
Универсальный код — для целых чисел в сжатии данных префиксный код, который преобразует положительные целые числа в двоичные слова, с дополнительным свойством: при любом истинном распределение вероятностей на целых числах, пока распределение монотонно… … Википедия
Универсальный код (сжатие данных) — Универсальный код для целых чисел в сжатии данных префиксный код, который преобразует положительные целые числа в двоичные слова, с дополнительным свойством: при любом истинном распределение вероятностей на целых числах, пока распространение … … Википедия
Вторичный алфавит — Эта статья о коде в теории информации, другие значения этого слова см. в код (значения). Код правило (алгоритм) сопоставления каждому конкретному сообщению строго определённой комбинации символов (знаков) (или сигналов). Кодом также называется… … Википедия
Декодирование — Эта статья о коде в теории информации, другие значения этого слова см. в код (значения). Код правило (алгоритм) сопоставления каждому конкретному сообщению строго определённой комбинации символов (знаков) (или сигналов). Кодом также называется… … Википедия
Кодовое слово — Эта статья о коде в теории информации, другие значения этого слова см. в код (значения). Код правило (алгоритм) сопоставления каждому конкретному сообщению строго определённой комбинации символов (знаков) (или сигналов). Кодом также называется… … Википедия
Первичный алфавит — Эта статья о коде в теории информации, другие значения этого слова см. в код (значения). Код правило (алгоритм) сопоставления каждому конкретному сообщению строго определённой комбинации символов (знаков) (или сигналов). Кодом также называется… … Википедия
Неравенство Крафта — Макмиллана — В теории кодирования, неравенство Крафта Макмиллана даёт необходимое и достаточное условие существования разделимых и префиксных кодов, обладающих заданным набором длин кодовых слов. Содержание 1 Предварительные определения 2 … Википедия
wiki.vspu.ru
портал образовательных ресурсов
Алфавитное неравномерное двоичное кодирование. Префиксный код. Код Хаффмана
Алфавитное неравномерное двоичное кодирование— кодирование при котором символы некоторого первичного алфавита кодируются комбинациями символов двоичного алфавита (т.е. 0 и 1), причем, длина кодов и, соответственно, длительность передачи отдельного кода, могут различаться.
Префиксный код в теории кодирования— код со словом переменной длины, имеющий такое свойство (выполнение условия Фано): если в код входит слово a, то для любой непустой строки b слова ab в коде не существует. Хотя префиксный код состоит из слов разной длины, эти слова можно записывать без разделительного символа.
Например, код, состоящий из слов 0, 10 и 11, является префиксным, и сообщение 01001101110 можно разбить на слова единственным образом:
Код, состоящий из слов 0, 10, 11 и 100, префиксным не является, и то же сообщение можно трактовать несколькими способами.
0 10 0 11 0 11 10
0 100 11 0 11 10
Префиксные коды широко используются в различных областях информационных технологий. На них основаны многие алгоритмы сжатия информации. Их используют различные протоколы. К префиксным кодам относятся такие распространённые вещи, как:
• Юникод,
• телефонные номера,
• Код Хаффмана,
• Код Фибоначчи и мн. другие.
Код Хаффмана
Идея, положенная в основу кодировании Хаффмана, основана на частоте появления символа в последовательности. Символ, который встречается в последовательности чаще всего, получает новый очень маленький код, а символ, который встречается реже всего, получает, наоборот, очень длинный код. Это нужно, так как мы хотим, чтобы, когда мы обработали весь ввод, самые частотные символы заняли меньше всего места (и меньше, чем они занимали в оригинале), а самые редкие — побольше (но так как они редкие, это не имеет значения). В данной статье я решил, что символ будет иметь длину 8 бит, то есть, будет соответствовать печатному знаку.
Я мог бы с той же простотой взять символ длиной в 16 бит (то есть, состоящий из двух печатных знаков), равно как и 10 бит, 20 и так далее. Размер символа выбирается, исходя из строки ввода, которую мы ожидаем встретить. Например, если бы я собрался кодировать сырые видеофайлы, я бы приравнял размер символа к размеру пикселя. Помните, что при уменьшении или увеличении размера символа меняется и размер кода для каждого символа, потому что чем больше размер, тем больше символов можно закодировать этим размером кода. Комбинаций нулей и единичек, подходящих для восьми бит, меньше, чем для шестнадцати. Поэтому вы должны подобрать размер символа, исходя из того по какому принципу данные повторяются в вашей последовательности.
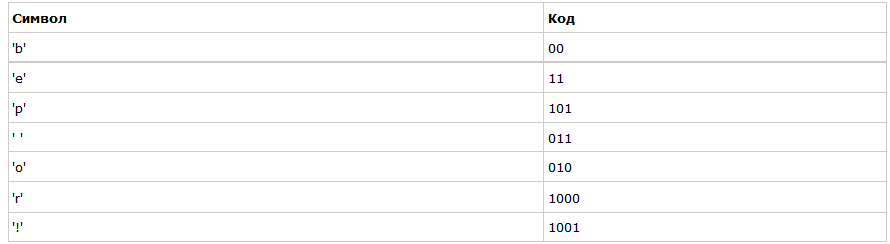
Предположим, у нас есть строка «beep boop beer!», для которой, в её текущем виде, на каждый знак тратится по одному байту. Это означает, что вся строка целиком занимает 15*8 = 120 бит памяти. После кодирования строка займёт 40 бит.
Чтобы получить код для каждого символа строки «beep boop beer!»,на основе его частотности, нам надо построить бинарное дерево, такое, что каждый лист этого дерева будет содержать символ (печатный знак из строки). Дерево будет строиться от листьев к корню, в том смысле, что символы с меньшей частотой будут дальше от корня, чем символы с большей. Скоро вы увидите, для чего это нужно.
Чтобы построить дерево, мы воспользуемся слегка модифицированной очередью с приоритетами — первыми из неё будут извлекаться элементы с наименьшим приоритетом, а не наибольшим. Это нужно, чтобы строить дерево от листьев к корню.
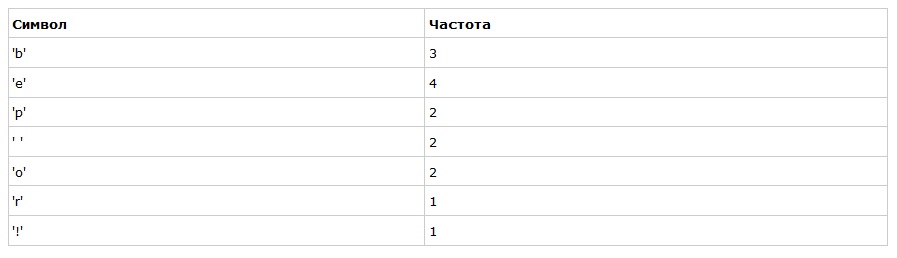
Для начала посчитаем частоты всех символов:
После вычисления частот мы создадим узлы бинарного дерева для каждого знака и добавим их в очередь, используя частоту в качестве приоритета:
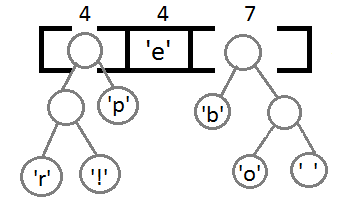
Теперь мы достаём два первых элемента из очереди и связываем их, создавая новый узел дерева, в котором они оба будут потомками, а приоритет нового узла будет равен сумме их приоритетов. После этого мы добавим получившийся новый узел обратно в очередь.
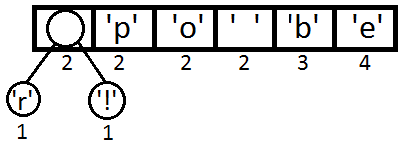
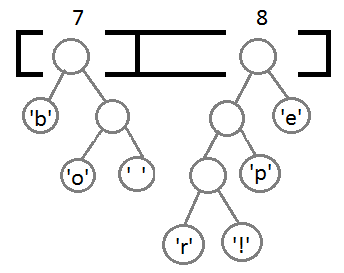
Повторим те же шаги и получим последовательно:
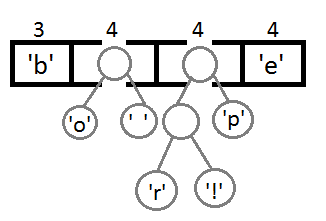
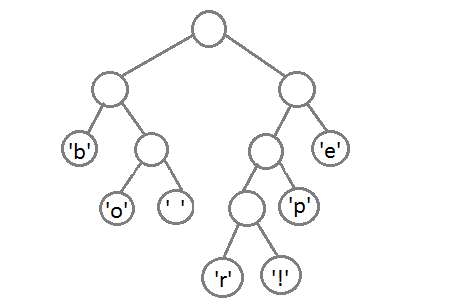
Ну и после того, как мы свяжем два последних элемента, получится итоговое дерево:
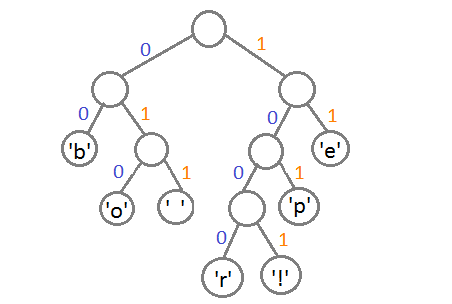
Теперь, чтобы получить код для каждого символа, надо просто пройтись по дереву, и для каждого перехода добавлять 0, если мы идём влево, и 1 — если направо:
Если мы так сделаем, то получим следующие коды для символов:
Чтобы расшифровать закодированную строку, нам надо, соответственно, просто идти по дереву, сворачивая в соответствующую каждому биту сторону до тех пор, пока мы не достигнем листа. Например, если есть строка «101 11 101 11» и наше дерево, то мы получим строку «pepe».
Важно иметь в виду, что каждый код не является префиксом для кода другого символа. В нашем примере, если 00 — это код для „b“, то 000 не может оказаться чьим-либо кодом, потому что иначе мы получим конфликт. Мы никогда не достигли бы этого символа в дереве, так как останавливались бы ещё на „b“.
Кодирование для чайников, ч.1
Не являясь специалистом в обозначенной области я, тем не менее, прочитал много специализированной литературы для знакомства с предметом и прорываясь через тернии к звёздам набил, на начальных этапах, немало шишек. При всём изобилии информации мне не удалось найти простые статьи о кодировании как таковом, вне рамок специальной литературы (так сказать без формул и с картинками).
Статья, в первой части, является ликбезом по кодированию как таковому с примерами манипуляций с битовыми кодами, а во второй я бы хотел затронуть простейшие способы кодирования изображений.
0. Начало
Давайте рассмотрим некоторые более подробно.
1.1 Речь, мимика, жесты
1.2 Чередующиеся сигналы
В примитивном виде кодирование чередующимися сигналами используется человечеством очень давно. В предыдущем разделе мы сказали про дым и огонь. Если между наблюдателем и источником огня ставить и убирать препятствие, то наблюдателю будет казаться, что он видит чередующиеся сигналы «включено/выключено». Меняя частоту таких включений мы можем выработать последовательность кодов, которая будет однозначно трактоваться принимающей стороной.
1.3 Контекст
2. Кодирование текста
Текст в компьютере является частью 256 символов, для каждого отводится один байт и в качестве кода могут быть использованы значения от 0 до 255. Так как данные в ПК представлены в двоичной системе счисления, то один байт (в значении ноль) равен записи 00000000, а 255 как 11111111. Чтение такого представления числа происходит справа налево, то есть один будет записано как 00000001.
Итак, символов английского алфавита 26 для верхнего и 26 для нижнего регистра, 10 цифр. Так же есть знаки препинания и другие символы, но для экспериментов мы будем использовать только прописные буквы (верхний регистр) и пробел.
Тестовая фраза «ЕХАЛ ГРЕКА ЧЕРЕЗ РЕКУ ВИДИТ ГРЕКА В РЕЧКЕ РАК СУНУЛ ГРЕКА РУКУ В РЕКУ РАК ЗА РУКУ ГРЕКУ ЦАП».
2.1 Блочное кодирование
Информация в ПК уже представлена в виде блоков по 8 бит, но мы, зная контекст, попробуем представить её в виде блоков меньшего размера. Для этого нам нужно собрать информацию о представленных символах и, на будущее, сразу подсчитаем частоту использования каждого символа:
Информационные технологии
Неравномерное кодирование. Средняя длина кодирования
В приведенных выше примерах кодирования все кодовые слова имели одинаковую длину. Однако это не является обязательным требованием. Более того, если вероятности появления сообщений заметно отличаются друг от друга, то сообщения с большой вероятностью появления лучше кодировать короткими словами, а более длинными словами кодировать редкие сообщений. В результате кодовый текст при определенных условиях станет в среднем короче.
Наиболее экономным является код с наименьшей средней длиной 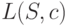
Пусть источник содержит 4 сообщения 


 | 00 |
 | 01 |
| A_3 | 10 |
| A_4 | 11 |
Очевидно, что для представления (передачи) любой последовательности в среднем потребуется 2 знака на одно сообщение. Сравним эффективность такого кодирования с описанным выше кодированием словами переменной длины. Кодовая таблица для данного случая может иметь следующий вид.
 | 0 |
 | 1 |
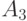 | 10 |
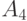 | 11 |
В этой таблице, в отличие от предыдущей, наиболее частые сообщения 

в то время как для равномерного кода средняя длина 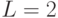
Необходимо отметить, что неоднозначность декодирования слова появилась несмотря на то, что условие однозначности декодирования знаков (инъективность кодового отображения) выполняется.
Решение данной проблемы заключается в том, чтобы иметь возможность в любом кодовом тексте выделять отдельные кодовые слова без использования специальных разделительных знаков. Иначе говоря, необходимо, чтобы код удовлетворял следующему требованию: всякая последовательность кодовых знаков может быть единственным образом разбита на кодовые слова. Коды, для которых последнее требование выполнено, называются однозначно декодируемыми (иногда их называют кодами без запятой).
Рассмотрим код (схему алфавитного кодирования) 
и различные слова, составленные из элементарных кодов.
Определение. Код 
Если таблица кодов содержит одинаковые кодовые слова, то есть если
то код заведомо не является однозначно декодируемым (схема не является разделимой). Такие коды далее не рассматриваются.
Префиксные коды
Наиболее простыми и часто используемыми кодами без специального разделителя кодовых слов являются так называемые префиксные коды [29].
Теорема 1. Префиксный код является однозначно декодируемым.
Множество кодовых слов можно графически изобразить как поддерево словарного дерева (рис.6.5). Для этого из всего словарного дерева следует показать только вершины, соответствующие кодовым словам, и пути, ведущие от этих вершин к корню дерева. Такое поддерево называют деревом кода или кодовым деревом.
Замечание. Свойство префиксности является достаточным, но не является необходимым для однозначной декодируемости.
Если код префиксный, то, читая кодовую запись подряд от начала, мы всегда сможем разобраться, где кончается одно кодовое слово и начинается следующее. Если, например, в кодовой записи встретилось кодовое обозначение 110, то разночтений быть не может, так как в силу префиксности наш код не содержит кодовых обозначений 1, 11 или, скажем, 1101. Именно так обстояло дело для рассмотренного выше кода, который очевидно является префиксным.