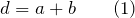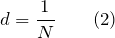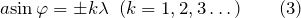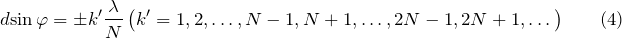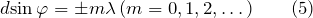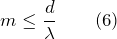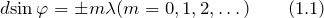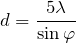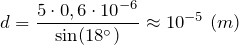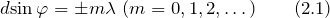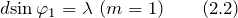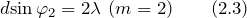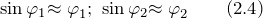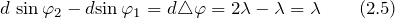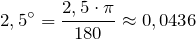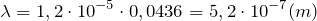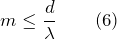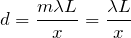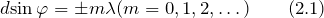что такое постоянная дифракционной решетки

Постоянная дифракционной решетки

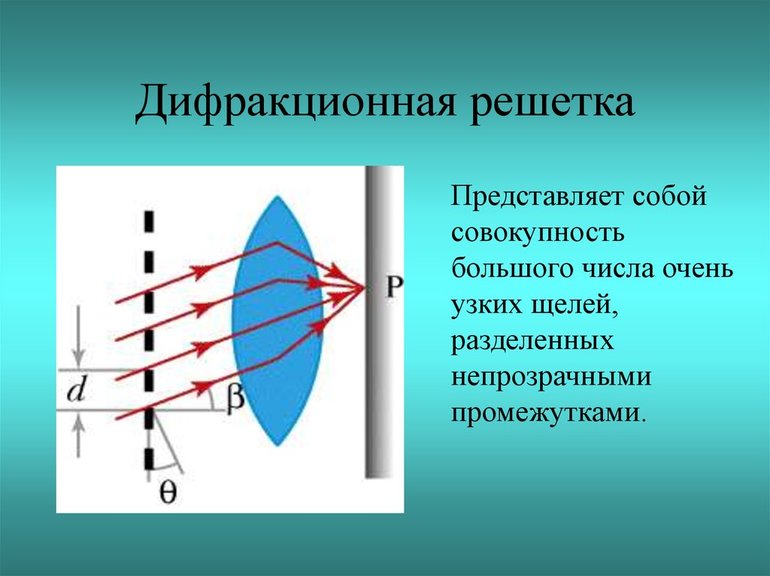
Общие сведения о дифракционной решетки

Дифракционная решетка является простейшим спектральным прибором. Она состоит из системы щелей, разделенных непрозрачными промежутками. Всю совокупность решеток делят на одномерные дифракционные решетки и многомерные. У одномерной дифракционной решетки параллельные участки прозрачные для света расположены в одной плоскости. Все прозрачные участки имеют одинаковую ширину. Прозрачные участки разделены непрозрачными промежутками. При помощи таких решеток исследования проводят в проходящем свете.

Используют так же отражающие дифракционные решетки. Эта решетка чаще всего – это полированная (зеркальная) металлическая пластина, на которой нанесены при помощи резца штрихи, рассеивающие свет. В результате дифракционная решетка является совокупностью участков, отражающих свет и его рассеивающих. Наблюдения в данном случае проводят в отраженном свете.

Дифракционная картина на решетке является результатом взаимной интерференции волн, идущих ото всех щелей. При использовании дифракционной решетки создается многолучевая интерференция когерентных пучков света, которые дифрагировали на щелях прибора.

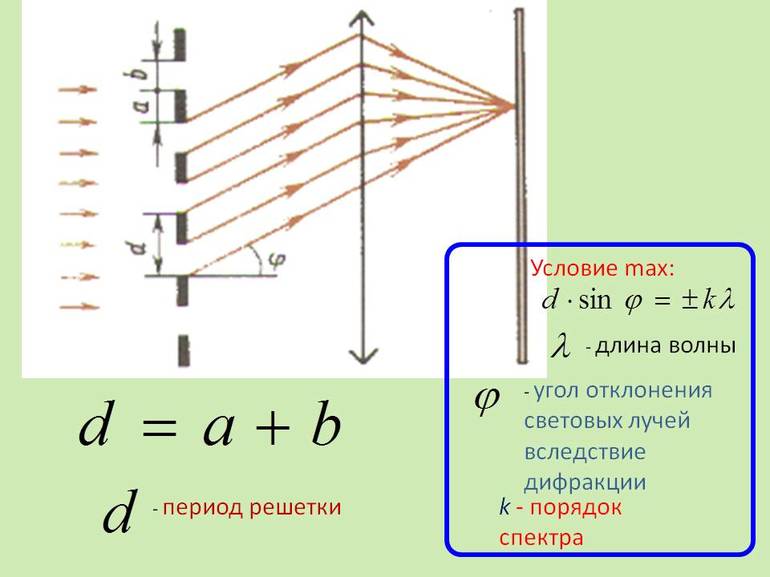
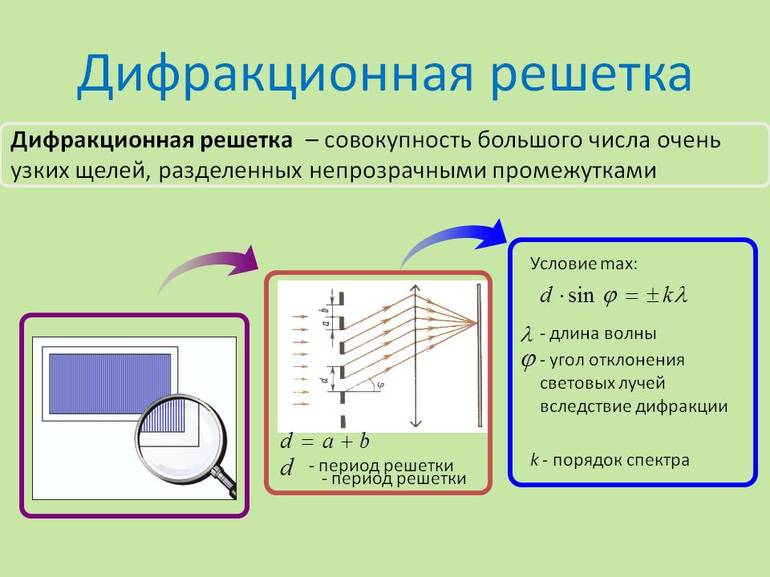
Пусть ширина щели решетки будет a, ширина непрозрачного участка – b, в таком случае сумма этих двух величин даст нам – это постоянную дифракционной решетки ( или ее период) (d):

Постоянная дифракционной решетки

Чаще всего изготавливают дифракционные решетки, которые имею период 10 мкм.

Период дифракционной решетки можно вычислить, если известно число штрихов (N), которыми обладает решетка на единицу своей длины:

Постоянная дифракционной решетки является одной из основных характеристик данного прибора. Она входит в формулы, которые характеризуют дифракционную картину, получаемую с ее помощью. При падении монохроматической волны на одномерную дифракционную решетку нормально к ее плоскости главные минимумы интенсивности наблюдаются в направлениях, которые определенны условием:

где 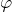– угол между нормалью к решетке и направлением распространения дифрагированных лучей.

Помимо основных минимумов, результатом взаимной интерференции световых лучей, которые посылает пара щелей, появляются дополнительные минимумы интенсивности. Они имеются в тех направлениях, где разность хода лучей равна нечетному числу половин волн:

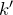
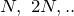
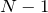
где N – число щелей дифракционной решетки; принимает любые целые значения кроме 0, . Если решетка обладает N щелями, то между двумя главными максимумами имеются дополнительный минимум, которые разделены вторичными максимумами.

Условием наличия главных максимумов дифракционной картины, получаемой при помощи решетки, является формула:

где m определяет порядок спектра.

Синус не может быть больше единицы, значит, количество главных максимумов (m):

При помощи дифракционной решетки проводят точные измерения длины волны. При известном периоде дифракционной решетки длину волны находят, измеряя угол 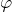, который соответствует направлению на максимум.

Примеры решения задач

Задание	Чему равна постоянная дифракционной решетки (d), если для монохроматического света длиной волны 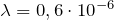м максимум пятого порядка отклонен на угол ?
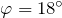Решение	В качестве основы для решения задачи примем условие существования главных максимумов дифракционной картины, получаемой при помощи решетки:

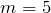
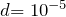По условию речь идет о максимуме пятого порядка, следовательно, . Выразим период дифракционной решетки:

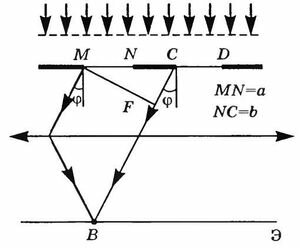
Ответм

Задание	Дифракционная решетка имеет постоянную, равную 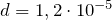м. На нее перпендикулярно ее поверхности падает волна длиной 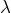. Какова длина волны света, если угол между спектрами первого и второго порядков составляет ?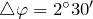
Решение	Сделаем рисунок.

Основой для решения задачи служит формула для максимумов интенсивности в картине дифракции:

Для максимума первого прядка имеем:

Для максимума второго порядка:

Так как мы имеем дело с малыми углами, то если их перевести в радианы, то можно считать, что:

Тогда разность уравнений (2.2) и (2.3) можно записать как:

Переведем 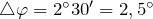в радианы:

Проведем вычисления длины волны:

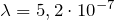Ответм

Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.

Источник

Учебники

Журнал «Квант»

Общие

Дифракционная решетка. Дифракционный спектр

Важную роль в прикладной оптике играют явления дифракции на отверстиях в форме щели с параллельными краями. При этом использование дифракции света на одной щели в практических целях затруднено из-за слабой видимости дифракционной картины. Широко используются дифракционные решетки.

Дифракционная решетка — спектральный прибор, служащий для разложения света в спектр и измерения длины волны. Различают прозрачные и отражающие решетки. Дифракционная решетка представляет собой совокупность большого числа параллельных штрихов одинаковой формы, нанесенных на плоскую или вогнутую полированную поверхность на одинаковом расстоянии друг от друга.

В прозрачной плоской дифракционной решетке (рис. 17.22) ширина прозрачного штриха равна а, ширина непрозрачного промежутка — Ь. Величина \(d = a + b = \frac<1> \) называется постоянной (периодом) дифракционной решетки, где N — число штрихов на единицу длины решетки.

Пусть плоская монохроматическая волна падает нормально к плоскости решетки (рис. 17.22). По принципу Гюйгенса—Френеля каждая щель является источником вторичных волн, способных интерферировать друг с другом. Получившуюся дифракционную картину можно наблюдать в фокальной плоскости линзы, на которую падает дифрагированный пучок.

Допустим, что свет дифрагирует на щелях под углом \(\varphi.\) Так как щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, для данного направления \(\varphi\) будут одинаковыми в пределах всей дифракционной решетки:

В тех направлениях, для которых разность хода равна четному числу полуволн, наблюдается интерференционный максимум. Наоборот, для тех направлений, где разность хода равна нечетному числу полуволн, наблюдается интерференционный минимум. Таким образом, в направлениях, для которых углы \(\varphi\) удовлетворяют условию

\(d \sin \varphi = m \lambda (m = 0,1,2, \ldots),\)

При наблюдении дифракции в немонохроматическом (белом) свете все главные максимумы, кроме нулевого центрального максимума, окрашены. Это объясняется тем, что, как видно из формулы \(\sin \varphi = \frac,\) различным длинам волн соответствуют различные углы, на которых наблюдаются интерференционные максимумы. Радужная полоска, содержащая в общем случае семь цветов — от фиолетового до красного (считается от центрального максимума), называется дифракционным спектром.

Ширина спектра зависит от постоянной решетки и увеличивается при уменьшении d. Максимальный порядок спектра определяется из условия \(

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — С. 517-518.

Источник

Период дифракционной решетки

Определение и общие сведения о дифракционной решетке

Дифракционные решетки подразделяют на одномерные и многомерные. Одномерная дифракционная решетка состоит из параллельных прозрачных для света участков одинаковой ширины, которые располагаются в одной плоскости. Прозрачные участки разделяют непрозрачные промежутки. При помощи данных решеток наблюдения проводят в проходящем свете.

Существуют отражающие дифракционные решетки. Такая решетка представляет собой, например, полированную (зеркальную) металлическую пластинку, на которую нанесены штрихи при помощи резца. В результате получают участки, которые отражают свет и участки, которые свет рассеивают. Наблюдение при помощи такой решетки проводят в отраженном свете.

Картина дифракции на решетке — это результат взаимной интерференции волн, которые идут ото всех щелей. Следовательно, при помощи дифракционной решетки реализуется многолучевая интерференция когерентных пучков света, которые подверглись дифракции и которые идут от всех щелей.

Период дифракционной решетки

Если ширину щели на решетки обозначим a, ширину непрозрачного участка – b, тогда сумма данных двух параметров – это период решетки (d):

Период дифракционной решетки иногда называют еще постоянной дифракционной решетки. Период дифракционной решетки можно определить как расстояние, через которое происходит повтор штрихов на решетке.

Постоянную дифракционной решетки можно найти, если известно количество штрихов (N), которые имеет решетка на 1 мм своей длины:

Период дифракционной решетки входит в формулы, которые описывают картину дифракции на ней. Так, если монохроматическая волна падает на одномерную дифракционную решетку перпендикулярно к ее плоскости, то главные минимумы интенсивности наблюдаются в направлениях, определенных условием:

где 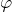– угол между нормалью к решетке и направлением распространения дифрагированных лучей.

Кроме главных минимумов, в результате взаимной интерференции световых лучей, которые посылает пара щелей, в некоторых направлениях они гасят друг друга, в результате появляются дополнительные минимумы интенсивности. Они возникают в направлениях, где разность хода лучей составляют нечетное число полуволн. Условие дополнительных минимумов записывают как:

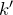
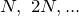
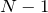
где N – число щелей дифракционной решетки; принимает любые целые значения кроме 0, Если решетка имеет N щелей, то между двумя главными максимумами находятся дополнительный минимум, которые разделяют вторичные максимумы.

Условием главных максимумов для дифракционной решетки служит выражение:

Величина синуса не может превышать единицу, следовательно, число главных максимумов (m):

Примеры решения задач

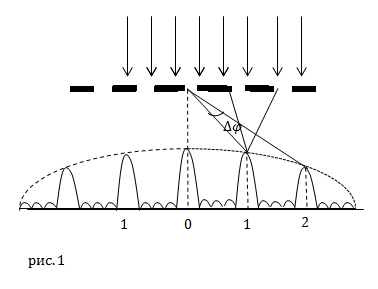
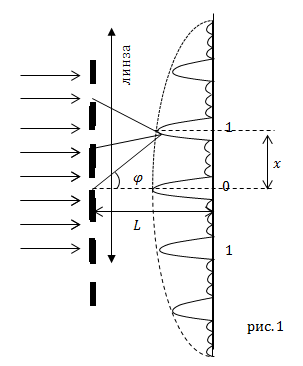
Задание	Сквозь дифракционную решетку проходит пучок света, имеющий длину волны 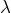. На расстоянии L от решетки размещается экран, на который при помощи линзы формируют картину дифракции. Получают, что первый максимум дифракции расположен на расстоянии x от центрального (рис.1). Каков период дифракционной решетки (d)?
Решение	Сделаем рисунок.

В основу решения задачи положим условие для главных максимумов картины дифракции:

По условию задачи речь идет о первом главном максимуме, то 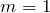. Из рис.1 получим, что:

Из выражений (1.2) и (1.1) имеем:

Выразим искомый период решетки, получаем:

Ответ

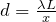
Задание	Каков период дифракционной решетки (d), если углу дифракции 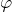будет соответствовать максимум k-го порядка? Длина волны света, падающего на дифракционную решетку равна .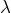
Решение	Условием главных максимумов для дифракционной решетки служит выражение:

По условию . Остается только выразить искомый период решетки:

Источник

Дифракционная решетка. Постоянная и период решетки. Использование в спектроскопии

Дифракционная решетка часто используется для определения спектра падающего на нее света, поскольку она позволяет расщеплять его на отдельные цвета. В данной статье рассмотрим, что такое дифракционная решетка, постоянная и период ее, и приведем пример решения задачи с использованием этого оптического прибора.

Явление дифракции

Суть его заключается в изменении направления распространения волны, когда она встречает на своем пути препятствие. Результат дифракции хорошо различим, если размеры препятствия сравнимы с длиной волны или меньше нее. Дифрагированная волна способна проникать в области за препятствием, куда она не смогла бы попасть, если бы двигалась вдоль прямой.

Вам будет интересно: Пузырь Алькубьерре — как передвигаться быстрее света?

На рисунке ниже приведен пример дифракции морской волны.

Видно, как прямой фронт волны после прохождения препятствия приобретает форму окружности.

Математическое описание дифракции осуществляется с использованием принципа Гюйгенса-Френеля, который гласит, что каждая точка волнового фронта является источником вторичной волны некоторой интенсивности.

Дифракция часто сопровождается интерференцией. Благодаря этим двум явлениям можно наблюдать так называемые дифракционные картины.

Дифракционная решетка

Это решетка представляет собой прозрачную пластинку, на которую нанесены непрозрачные штрихи с определенным периодом. Когда свет проходит через такую пластинку, то она вносит периодическое возмущение в его волновой фронт. В результате возникает ряд вторичных источников, которые испускают когерентные волны. В результате интерференции когерентные волны образуют на экране совокупность максимумов и минимумов, то есть дифракционную картину.

Описанная выше решетка называется проходящей или прозрачной. Существует также отраженная дифракционная решетка, которая представляет собой совокупность периодических бороздок, нанесенных на гладкую поверхность материала. Примером этого вида решетки является DVD-диск.

Уравнение решетки

В приближении дальнего поля (дифракция Фраунгофера) уравнение для решетки выглядит следующим образом:

Приведенная формула непосредственно следует из условия интерференционного максимума. В лабораторных работах ее используют для определения либо постоянной дифракционной решетки, когда λ известна, либо длины волны, когда d известен.

Использование дифракционной решетки в спектроскопии

Приведенное выше уравнение решетки позволяет сделать вывод, что углы θm, в которых появляются максимумы, зависят от длины волны. Чем больше она, тем больше эти углы (длинные волны лучше дифрагируют, чем короткие). Это означает, что если на решетку направить белый свет, то она его разложит на ряд цветов подобно дисперсионной призме. Причем последовательность цветов, начиная от центра (m=0), будет идти от фиолетового к красному.

Каждый максимум для соответствующего порядка дифракции и белого света будет представлять собой «радугу». Единственным максимумом, который всегда будет белым, является центральный или нулевой (m=0).

Явление разложения белого света на отдельные составляющие позволяет использовать дифракционную решетку в спектроскопии. Например, пропуская свет от далекой галактики через решетку, а затем анализируя полученный спектр, можно с достоверностью сказать, какие элементы присутствуют в галактике, какая у них температура, с какой скоростью движется эта галактика относительно нас (в последнем случае учитывается эффект Доплера).

Пример решения задачи

Покажем, как пользоваться уравнением решетки, на примере решения простой задачи. Пусть постоянная дифракционной решетки равна 300 штрихов на 1 мм. Необходимо определить, при каком угле будет наблюдаться максимум первого порядка для фиолетовой (400 нм) и для красной (700 нм) волн.

Учитывая, что число штрихов N обратно пропорционально периоду d, перепишем уравнение решетки в виде:

Угол для первого максимума равен:

Подставляем данные в единицах СИ в это выражение, получаем:

Для фиолетового: θ1 = arcsin(400*10-9*300*103) = 6,89o.

Для красного: θ1 = arcsin(700*10-9*300*103) = 12,12o.

Если экран поставить на расстоянии 1 метра от решетки, тогда на нем красная и фиолетовая полосы для первого порядка дифракции будут находиться на расстоянии около 9 см друг от друга.

Источник

Зона Френеля

При поддержке ДР осуществляется взаимное наращивание многолучевого распространения или уменьшение амплитуды когерентных световых пучков, которые считаются дифракционными. Правильное определение принципа Гюйгенса-Френеля: плоскость волны в любой момент является не простой оболочкой вторичных линий, а результатом их интерференции.

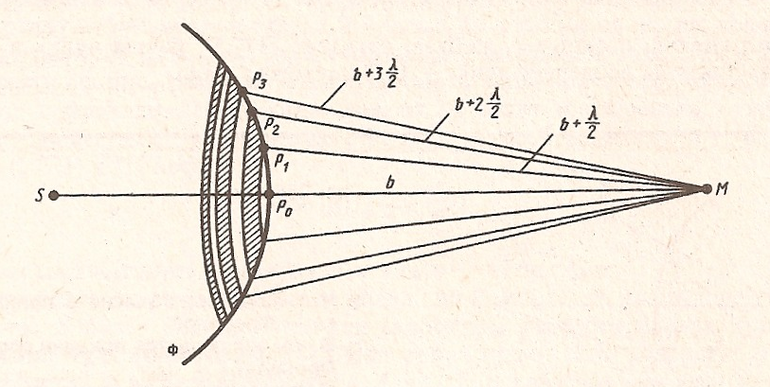
Чтобы найти амплитуду световой волны от монохроматического точечного источника света в случайной точке O изотропной среды, необходимо обрамить основные устройства шаром с радиусом r = QD. Интерференция волн от вторичных источников, расположенных на плоскости, определяет амплитуду в рассматриваемой точке О, то есть необходимо добавить когерентные колебания от всех вторичных объектов на плоскости волны.

Поскольку расстояния от них до точки О различны, барабаны начнут растягиваться в разные фазы. Длина кратчайшего пути от точки O до плоской волны равна 0. Первая зона Френеля ограничена точками плоскости, расстояния от которых до точки О такие же. Края других зон нацелены таким же образом. Когда отличие траекторий от двух соседних зон составляет половину длины волны, барабаны из них попадают в точку О в циркулирующих фазах, появляется небольшое количество шума, если разность траекторий равна длине волны интерференции.

Таким образом, если препятствие соответствует целому числу линий волн, оно станет взаимно скомпенсированным, и в этой точке будет замечено чёрное пятнышко. В случае нечётного числа полуволн, это красочное пятно. Расчёты могут помочь правильно понять, каким образом свет от точечного источника, излучающего сферические волны, достигает случайной точки в пространстве.

Дифракция от всех типов препятствий:

Наблюдение при исследовании

Дифракция происходит на объектах любого размера, а не только пропорционально длине волны λ. Сложность исследования заключается в том, что из-за малой длины световой волны максимумы интерференции находятся достаточно близко друг к другу, а их интенсивность быстро уменьшается. ДФ может великолепно следовать на расстоянии.

Если дифракция незаметна и происходит затемнение, объект невидим, появляется резкая тень. Диаметр экрана D определяет границу геометрической оптики. Если наблюдение выполняется на расстоянии, волновые свойства света начинают проявляться в пропорциях применимости геометрической оптики, где d-величина объекта.

Шаблоны распределения шума из разных точек объекта перекрываются, и изображение становится размытым, в результате чего устройство не выделяет отдельные части объекта. Дифракция может наблюдаться и определяет разрешение любого оптического устройства.

Человеческому глазу оно видно примерно под тем же углом:

Можно видеть объекты, размеры которых сопоставимы с длиной линии света.

Дифракционная особенность

Световая дифракция — предельное отклонение лазерного луча и изменение направления волны. Отклонение силы разложения связано с прохождением света через сетку, которая содержит многочисленные щели. Дифракционная сетка является тем лучше, чем большее количество зазоров содержит уплотнение.

Ширина щели сравнима с размером световой волны. Когда лазерный свет проходит через зазор в дифракционной сетке, происходит дифракция света. Период дифракционной решётки обладает свойством: когда последовательный лазерный луч проходит через несколько зазоров, плотно расположенных рядом друг с другом, происходят помехи волн (перекрытие) и на экране можно наблюдать полосы.

Прибор главной оптики состоит из большого числа параллельных равноудалённых черт одинаковой формы, нанесенных на плоскую или вогнутую подложку, где происходит дифракция падающей волны. Обычно это прозрачная пластина или металлическое зеркало с плотно нанесёнными — более 1 тыс. в 1 мм — трещинами или с полосками, полученными методами голографии. Возникающие щели вызывают угловой прогиб дисперсии, проходящих (отражённых) линейных лучей света.

Собранные через линзу лучи дают на экране в случае монохроматического света изображение бликов (очередные яркие полоски возникают в направлениях, для которых различия оптики и интерференционных пучков являются целым кратным длине линии сгибаемого света), а в случае белого света — непрерывным спектром. Особым типом дифракционной сетки является ступенчатая (отражающая), построенная А. Михельсоном. ДР является основным компонентом большинства спектральных приборов.

Спектральный анализ

ДС является инструментом для проведения спектрального анализа света. Она образует систему равных, параллельных и одинаково расположенных зазоров. Используется для точных измерений длин световых волн и представляет собой систему препятствий для линий, расположенных в пространстве или на поверхности, периодически или случайно. Препятствий возникает явление дифракции (отсюда и название сетки).

Постоянная дифракционная решётка — параметр, характеризующий сетку. Он выражает расстояние между отверстиями (щелями). Зависимость значения постоянной линии и угла изгиба α представляет формулу дифракционной решётки:

общее уравнение — nλ = d•sina

Фиксированная сетка может легко измеряться:

Установить устройство следует таким образом, чтобы солнце хорошо светило на панель, расположенную в его узкой части. Там размещена ДС. Смотреть изображение нужно фокусирующим экраном. Следует обратить внимание, что наблюдаемые оттенки расположены в обратном порядке, чем призма. Красный цвет является наиболее сильно отклоняемым от направления света, падающего на сетку, а фиолетовая гамма на третьем месте.

Особенности явления

Дифракционная сетка представляет собой плотно очерченную пластину, которая может содержать до тысячи зазоров на миллиметр. Солнечный свет в этом опыте проявляет волновую природу, проходя через щели, наклоняется и качается. Это явление носит название отклонения и есть на каждом слоте сетки. Расходящиеся с прорезями волны накладываются друг на друга и усиливаются в определённых местах (различных для света длины волны и разного цвета), что называют излучением. Благодаря дифракции и интерференции можно наблюдать спектр солнечного света с цветами, расположенными в обратном порядке, чем в призме.

Дифракционные сетки используются при строительстве спектрометров — устройств, используемых для разделения света на его составляющие. Такой анализ позволяет определить, какие химические элементы входят в объект. Благодаря анализу спектра учёные могут определить химический состав даже очень далёких звёзд. Аналогичным образом преобразуются радужные блики, наблюдаемые, когда свет отскакивает от компакт-диска.

Когда необходимо разделить свет с разными длинами волн с высоким разрешением, дифракционная решётка является наиболее предпочтительным инструментом. Этот «суперпризменный» аспект приводит ДС к применению для измерения атомных спектров как в лабораторных приборах, так и в телескопах.

Условие максимальной интенсивности такое же, как и для двойной щели или нескольких, но большое количество зазоров обеспечивает высокое разрешение для применения в спектроскопии, то есть результат может отличаться. Различные длины волн дифрагируют под разными углами в зависимости от классификации сетки. Важна разрешающая способность дифракционной решётки и некоторые другие характеристики.

Источник