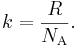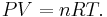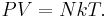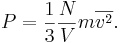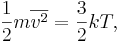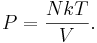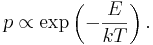что такое постоянная больцмана в физике определение
Постоянная Больцмана
Постоянной Больцмана называется физическая постоянная, с помощью которой определяется связь между энергией и температурой.
Не следует путать ее с постоянной Стефана-Больцмана, связанной с излучением энергии абсолютно твердого тела.
Существуют различные методы вычисления данного коэффициента. В рамках этой статьи мы рассмотрим два их них.
Нахождение постоянной Больцмана через уравнение идеального газа
Для этого запишем уравнение дважды, подставив в него параметры состояний.
Зная результат, можем найти значение параметра k :
Нахождение постоянной Больцмана через формулу броуновского движения
Для второго способа вычисления нам также потребуется провести эксперимент. Для него нужно взять небольшое зеркало и подвесить в воздухе с помощью упругой нитки. Допустим, что система зеркало-воздух находится в стабильном состоянии (статическом равновесии). Молекулы воздуха ударяют в зеркало, которое, по сути, ведет себя как броуновская частица. Однако с учетом его подвешенного состояния мы можем наблюдать вращательные колебания вокруг определенной оси, совпадающей с подвесом (вертикально направленной нитью). Теперь направим на поверхность зеркала луч света. Даже при незначительных движениях и поворотах зеркала отражающийся в нем луч будет заметно смещаться. Это дает нам возможность измерить вращательные колебания объекта.
Следующее уравнение является законом сохранения энергии, который будет выполняться для данных колебаний (то есть потенциальная энергия будет переходить в кинетическую и обратно). Мы можем считать эти колебания гармоническими, следовательно:
При выведении одной из формул ранее мы использовали закон равномерного распределения энергии по степеням свободы. Значит, можем записать так:
Следовательно, зная основы броуновского движения, мы можем найти постоянную Больцмана с помощью измерения макропараметров.
Значение постоянной Больцмана
Значение изучаемого коэффициента состоит в том, что с его помощью можно связать параметры микромира с теми параметрами, что описывают макромир, например, термодинамическую температуру с энергией поступательного движения молекул:
Этот коэффициент входит в уравнения средней энергии молекулы, состояния идеального газа, кинетической теории газа, распределение Больцмана-Максвелла и многие другие. Также постоянная Больцмана необходима для того, чтобы определить энтропию. Она играет важную роль при изучении полупроводников, например, в уравнении, описывающем зависимость электропроводности от температуры.
Переходим к определению количества степеней свободы молекулы:
Сначала вычислим общую массу смеси.
Теперь из данного уравнения выразим концентрацию первого газа:
Далее нам потребуется уравнение, описывающее состояние идеального газа:
Подставим полученное равнее значение:
Поскольку молярные массы газов нам известны, мы можем найти массы молекул первого и второго газа:
Исторические данные
Как точная наука, физика не считается абсолютной без набора довольно весомых констант, которые интегрируются как универсальные коэффициенты в уравнения, устанавливающие связь между какими-либо величинами. Это фундаментальные элементы, благодаря которым многие вещи приобретают неизменность.
Между этими характеристиками, присущими материи Вселенной, существует постоянная Больцмана, значение которой входит в ряд весомых уравнений. Стоить сказать об определённом количестве решений с помощью неизменной.
Законы Ньютона управляют силами, массами и движениями объектов или систем и считаются детерминированными: то есть тот, кто полностью знает начальные условия в системе, может точно предсказать будущее. Именно так космические миссии размещают посадочные модули роботов в определённых желаемых местах в сотнях миллионов километров от Земли.
Для огромного комплекса объектов, таких как миллиарды триллионов горячих молекул, движущихся в паровом двигателе, доминирующей единицей расчёта является постоянная Больцмана, но невозможно определить состояние каждой независимой частицы: они движутся с разными скоростями и энергетическими диапазонами.
Например, молекулы воздуха при комнатной температуре 25 градусов по Цельсию (300 Кельвинов, или 77 гр. по Фаренгейту) движутся со средней скоростью около 500 метров в секунду (1100 миль в час). Но некоторые движутся 223 м/с и 717 м/с и так далее, и все они идут в разных направлениях. Каждое их свойство не может быть известно.
Однако понимание физики тепловых явлений требует некоторого способа сделать математически полезные утверждения о коллекциях огромного числа объектов. Больцман и другие учёные показали, что это можно вычислить с точки зрения статистики и вероятностей механики. Коллективные термодинамические свойства комбинаций вытекают из суммы энергий каждого отдельного объекта. Интересно, что разные значения энергии имеют иные вероятности возникновения. Для вычислений нужно знать, чему равно значение постоянной Больцмана. Вот уравнение: E=32kT
Молекулы и тепловые вещества
Физический смысл постоянной Больцмана и температуры применяется к свойству степени нагрева тела. В физике используется безусловная шкала, основанная на выводе молекулярно-кинетической доктрины в качестве меры, показывающей количество энергии теплового движения частиц.
Данные для вычислений, используемые в системе СГС, считаются очень большими единицами, чтобы выразить энергию молекул, и, таким образом, довольно сложно измерить температуру этим способом. Удобной единицей снятия данных считается градус, и данные фиксируются косвенно, путём регистрации изменяющихся макроскопических показаний вещества.
В однородном безупречном газе при определённой температуре энергия на любом поступательном уровне свободы равна, как следует из определения Максвелла. При комнатной температуре эта энергия равна j или 0,013 эВ. В одноатомном безупречном газе любой атом содержит 3 степени свободы, это соответствует 3 пространственным осям, что фактически означает, что любой атом содержит энергию B. С учётом тепловой энергии можно определить среднее значение квадрата скорости атомов, которое обратно пропорционально корню массы.
Особенности энергии
Для расчёта веществ при температурах и давлениях, ближайших к обычным, применяется совершенная газовая модель, то есть та, величина молекулы которой гораздо меньше занята конкретной численностью веществ, а расстояние между частичками гораздо больше радиуса их взаимодействия. Основываясь на уравнениях кинетической доктрины, средняя энергия этих частиц нацелена как ECP = 3/2 ∙ kT, где E-кинетическая энергия, T-температура, а 3/2 — коэффициент пропорциональности K, введённый Больцманом.
Численность здесь характеризует:
Смысл k, который позднее был назван в честь Больцмана, демонстрирует, сколько Джоулей на уровне 1. В иных доктринах его смысл определяет, как статистически, в среднем, энергия термического неселективного перемещения 1-го моноатомного безупречного газа возрастает с температурой на 1 градус.
Статистическое рассредотачивание
Так как макроскопические состояния материи считаются итогом поведения большого числа частиц, они описываются статистическими способами. Последнее подразумевает выяснение того, как распределяются энергосвойства молекул газа.
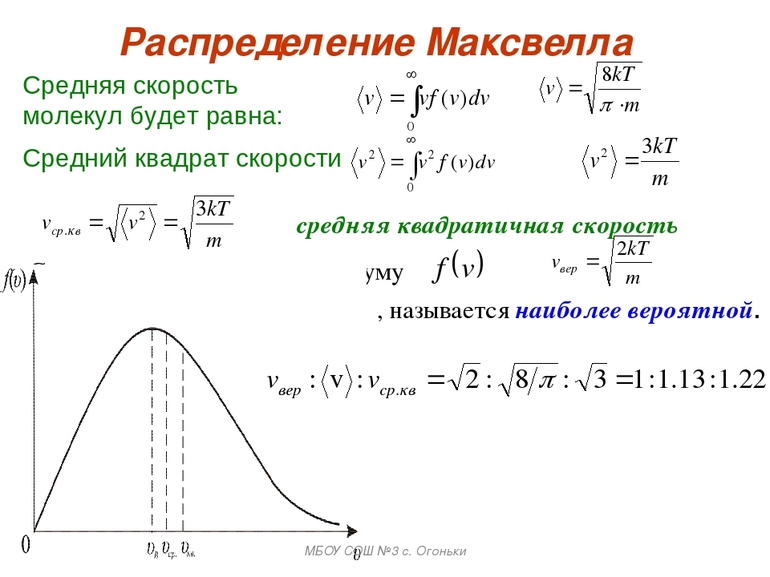
Рассредотачивание кинетических скоростей по Максвеллу происходит по-разному. Практически он показывает, что в равновесном газе главное множество молекул содержит части, более близкие к вероятным v = √ (2kT / m0), где m0-масса молекулы.
Определение Больцманом возможных энергий для газов будет пребывать на фоне всякой силы, к примеру, гравитации. Это зависит от пропорции 2-х вещей:
В итоге чем меньше возможность энергии молекул (ближе к плоскости планеты), тем выше их сосредоточение.
Оба статистических способа связаны с рассредотачиванием Максвелла-Больцмана, содержащим экспоненциальный коэффициент eE / kT, где E — сумма кинетической и возможной энергий, а kT — средняя сила термического смещения, обусловленная ПБ. Формула постоянной Больцмана — коэффициент, равный k=1,38·10−23 ДжК.
Константа пропорциональности неизменна по Больцману. Это выражение, которое определяет связь между микроскопическим и макроскопическим состояниями, выражает центральную идею статистической механики. Планковское число измерений температуры составляет 1 416 785 (71) • 1032 К, что фактически соответствует энергии массового спокойствия.
Безграничная материя
С точки зрения теории неограниченного погружения материи, ПБ является величиной только 1-го атомного смысла. Как показывает идеальный тест физических единиц измерения значений, при использовании шкалы температуры и тепловой энергии, содержащиеся в единице количества вещества, они считаются неизменными. Отсюда выделяют данные, практически используя температуру как физическое определение на одном уровне. Вещества могут быть пересчитаны по значению неизменной со вступлением надлежащих коэффициентов схожести. Теоретическим критерием этой процедуры считается SPF-симметрия.
Можно получить определение звёздного неба и по теории Планка оно будет простым минусом импульса объектов. Его данные также равны понятию Kps = K ∙ f = 9,187 ∙ 1032 Дж / К, где f — коэффициент однородности массы.
ПБ определяет ассоциация между действенной температурой большого количества обычных звёздных объектов как меру термической энергии и средней кинетической при смещении. Не считая того, что она связывает внутреннюю температуру объектов с имеющейся энергией. Такие константы могут быть рассчитанными для любого значения материи.
В результате ПБ:
Измерение постоянной Больцмана является одной из ведущих констант. Это не только разрешает установить ассоциацию между линиями микроскопичных явлений молекулярного значения с параметрами процессов, наблюдаемых в макромире. И дело не только в том, что эта величина включена в ряд значимых уравнений.
В настоящем времени непонятно, есть ли какой-нибудь вещественный принцип произведения, на базе которого он имел бы возможность получить вывод на теоретическом уровне. В иных доктринах ничего не рассказывается об этом. На самом деле смысл этой константы может быть практически схожим с другими величинами.
Изменения в фиксации постоянной
Хотя Кельвин не был основан на физическом артефакте, его изменение также важно. Более раннее определение размерности было основано на специфических свойствах универсальной постоянной природы. Основываясь на постоянной Стефана Больцмана, Кельвин также используют учёные, применя букву K в вычислениях. Это позволяет измерениям температуры быть действительно универсальными.
Постоянная Больцмана
Для постоянной, связанной с энергией излучения чёрного тела, смотри Постоянная Стефана-Больцмана
Значение постоянной k [1]
1,380 6504(24) • 10 −23
Смотри также Значения в различных единицах ниже.
Постоянная Больцмана ( k или kB ) — физическая постоянная, определяющая связь между температурой вещества и энергией теплового движения частиц этого вещества. Названа в честь австрийского физика Людвига Больцмана, сделавшего большой вклад в статистическую физику, в которой эта постоянная играет ключевую роль. Её экспериментальное значение в системе СИ равно
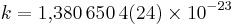
В таблице последние цифры в круглых скобках указывают стандартную погрешность значения постоянной. В принципе, постоянная Больцмана может быть получена из определения абсолютной температуры и других физических постоянных. Однако точное вычисление постоянной Больцмана с помощью основных принципов слишком сложно и невыполнимо при современном уровне знаний.
Экспериментально постоянную Больцмана можно определить с помощью закона теплового излучения Планка, описывающего распределение энергии в спектре равновесного излучения при определённой температуре излучающего тела, а также другими методами.
Существует связь между универсальной газовой постоянной 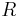
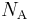
Размерность постоянной Больцмана такая же, как и у энтропии.
Содержание
История
В 1877 г. Больцман впервые связал между собой энтропию и вероятность, однако достаточно точное значение постоянной k как коэффициента связи в формуле для энтропии появилось лишь в трудах М. Планка. При выводе закона излучения чёрного тела Планк в 1900–1901 гг. для постоянной Больцмана нашёл значение 1,346 • 10 −23 Дж/K, почти на 2,5% меньше принятого в настоящее время. [2]
До 1900 г. соотношения, которые сейчас записываются с постоянной Больцмана, писались с помощью газовой постоянной R, а вместо средней энергии на одну молекулу использовалась общая энергия вещества. Лаконичная формула вида S = k log W на бюсте Больцмана стала таковой благодаря Планку. В своей нобелевской лекции в 1920 г. Планк писал: [3]
Эта константа часто называется постоянной Больцмана, хотя, насколько я знаю, сам Больцман никогда не вводил её — странное состояние дел, при том, что в высказываниях Больцмана не было речи о точном измерении этой константы.
Такая ситуация может быть объяснена проведением в то время научных дебатов по выяснению сущности атомного строения вещества. Во второй половине 19 века существовали значительные разногласия в отношении того, являются ли атомы и молекулы реальными, либо они лишь удобный способ описания явлений. Не было единства и в том, являются ли «химические молекулы», различаемые по их атомной массе, теми же самыми молекулами, что и в кинетической теории. Далее в нобелевской лекции Планка можно найти следующее: [3]
«Ничто не может лучше продемонстрировать положительную и ускоряющуюся скорость прогресса, чем искусство эксперимента за последние двадцать лет, когда было открыто сразу множество методов измерения массы молекул практически с той же точностью, что и измерение массы какой-нибудь планеты».
Уравнение состояния идеального газа
Для идеального газа справедлив объединённый газовый закон, связывающий давление P, объём V, количество вещества n в молях, газовую постоянную R и абсолютную температуру T:
В данном равенстве можно сделать замену 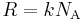
Связь между температурой и энергией
Соотношения газовой термодинамики
Кинетическая теория даёт формулу для среднего давления P идеального газа:
Учитывая, что средняя кинетическая энергия прямолинейного движения равна:
находим уравнение состояния идеального газа:
Это соотношение неплохо выполняется и для молекулярных газов; однако зависимость теплоёмкости изменяется, так как молекулы могут иметь дополнительные внутренние степени свободы по отношению к тем степеням свободы, которые связаны с движением молекул в пространстве. Например, двухатомный газ имеет уже приблизительно пять степеней свободы.
Множитель Больцмана
В общем случае система в равновесии с тепловым резервуаром при температуре T имеет вероятность p занять состояние с энергией E, что может быть записано с помощью соответствующего экспоненциального множителя Больцмана:
В данном выражении фигурирует величина kT с размерностью энергии.
Вычисление вероятности используется не только для расчётов в кинетической теории идеальных газов, но и в других областях, например в химической кинетике в уравнении Аррениуса.
Роль в статистическом определении энтропии
Постоянная Больцмана
Краткое описание
Постоянная Больцмана — физическая постоянная, определяющая связь между температурой и энергией.
Взаимосвязь между макроскопическими свойствами материи (давление, температура) и характером движения атомов и молекул описывается молекулярно-кинетической теорией. Одним из ее создателей являлся Людвиг Больцман.
В рамках этой теории температура газа объясняется кинетической энергией его молекул (скоростью движения), а давление — их упругими ударами о стенки сосуда. Это соотношение устанавливает формула:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
где m — масса молекул газа, v — их средняя скорость, k — постоянная Больцмана, а T — температура газа по шкале Кельвина.
Физический смысл постоянной Больцмана заключается в обеспечении взаимосвязи характеристик атомно-молекулярного уровня и объемными свойствами газа, которые можно измерить при помощи приборов.
Постоянная Больцмана обозначается буквой k, а ее величина равна
Как соотносится энергия и температура
В идеальном одноатомном газе каждый атом имеет три степени свободы, которые соответствуют трем пространственным осям. Поэтому энергию, приходящуюся на каждый атом можно выразить как
Если известна величина тепловой энергии, то нетрудно рассчитать среднеквадратичную скорость атомов. Она будет обратно пропорциональна корню квадратному из атомной массы. Например, при температуре 300 К среднеквадратичная скорость молекул ксенона составит 240 м/с, а гелия — 1370 м/с.
Вычисления для молекулярного газа усложняются. Это связано с увеличением степеней свобод. Так, например, при низкой температуре двухатомный газ имеет уже две вращательных и три поступательных степеней свободы. Рассмотрим решение конкретной задачи.
Задача
Газ состоит из N-атомных объемных молекул и находится при определенной температуре Т, при которой у молекул возбуждены колебательные, вращательные и поступательные степени свободы. Найти среднюю энергию молекул этого газа.
На каждую степень свободы в среднем приходится одинаковая величина кинетической энергии (закон равномерного распределения энергии по степеням свободы), которая равна
Тогда можно утверждать, что средняя энергия молекулы составит
Сделаем небольшое пояснение: i — сумма поступательных, вращательных и удвоенного количества колебательных степеней свободы, то есть
Теперь необходимо определить сколько степеней свободы имеют молекулы рассматриваемого газа:
Сокращаем полученное выражение и получаем:
Ключевые нюансы
Постоянная Больцмана представляет собой отношение газовой постоянной (R) к постоянной Авогадро (Na):
По состоянию на 2017 год в международной системе единиц (СИ) ее значение составляет
а размерность — Дж/К.
Постоянную Больцмана не следует путать с постоянной Стефана-Больцмана, которая является константой пропорциональности в законе Стефана-Больцмана.
Способы нахождения постоянной Больцмана
Для нахождения постоянной Больцмана можно использовать различные методы.
Универсальный метод
Искомый коэффициент входит в уравнение состояния идеального газа:
Многочисленные опыты показывают, что при нагревании любого газа от T0=273 К до Т1=373 K его давление на стенки сосуда увеличивается с \(P_0=1.013\times10^5\) Па до \(P_1=1.38\times10^5 Па.\)
Провести такой опыт совсем несложно. В качестве газа используется обычный воздух, давление измеряется при помощи манометра, а температура — термометра. При этом известно, что один моль любого газа при нормальных условиях занимает объем V=22,4 л и содержит \(6.02\times10^<23>\) молекул.
Подставим известные параметры в уравнение состояния идеального газа:
Отсюда, коэффициент k
Подставив в получившиеся уравнение известные данные и решив его получаем значение постоянной Больцмана равное \(1.38\times10^<-23>.\)
Через формулу броуновского движения
Небольшое зеркальце подвешивают на упругой нити. Система зеркало-воздух находится в статическом равновесии. О поверхность зеркала ударяются хаотично движущиеся молекулы воздуха. Поэтому оно ведет себя как одна из броуновских частиц. Помимо этого, зеркало будет совершать и крутильные колебания вокруг оси, которой является упругая нить-подвес.
Зеркальную поверхность освещают лучом света. При ее, даже небольших поворотах, отраженный луч будет смещаться. Это позволяет не только увидеть, но и измерить крутильные колебания.
Умножив обе части уравнения на \(\varphi\) и преобразовав его получаем:
Так как малые крутильные колебания являются гармоничными, то можно записать:
Исходя из него получаем:
Подставив в полученную формулу полученные опытным путем данные, например
Получаем приблизительное значение постоянной Больцмана равное
Области применения
Постоянная Больцмана является важным членом многих уравнений:
Кроме того, постоянная Больцмана играет роль в распределении энергии, используется в определении энтропии. Немаловажное значение имеет эта константа и в физике полупроводников. Она входит в состав формулы, описывающей зависимость между электропроводимостью и температурой.
| Значения k | Единицы измерения |
|---|---|
| 1,380 649 × 10 −23 | Дж ⋅ К −1 |
| 8,617 333 262 145 × 10 −5 | эВ ⋅ K −1 |
| 1,380 649 × 10 −16 | эрг ⋅ K −1 |
Подробнее см. § Значение в различных единицах ниже.СОДЕРЖАНИЕРоли постоянной БольцманаМакроскопически закон идеального газа гласит, что для идеального газа произведение давления p и объема V пропорционально произведению количества вещества n (в молях ) и абсолютной температуры T : Роль в равнораспределении энергииКинетическая теория дает среднее давление p для идеального газа как Сочетание с законом идеального газа показывает, что средняя поступательная кинетическая энергия равна Уравнению идеального газа также строго подчиняются молекулярные газы; но форма для теплоемкости более сложна, потому что молекулы обладают дополнительными внутренними степенями свободы, а также тремя степенями свободы для движения молекулы в целом. Например, двухатомные газы обладают в общей сложности шестью степенями простой свободы на молекулу, которые связаны с движением атомов (три поступательных, два вращательных и одна колебательная). При более низких температурах не все эти степени свободы могут полностью участвовать в теплоемкости газа из-за квантово-механических ограничений на доступность возбужденных состояний при соответствующей тепловой энергии на молекулу. Роль в факторах БольцманаВ более общем смысле, системы, находящиеся в равновесии при температуре T, имеют вероятность P i занять состояние i с энергией E, взвешенной с помощью соответствующего фактора Больцмана : Роль в статистическом определении энтропииЭто уравнение, которое связывает микроскопические детали или микросостояния системы (через W ) с ее макроскопическим состоянием (через энтропию S ), является центральной идеей статистической механики. Его важность такова, что он начертан на надгробии Больцмана. Константа пропорциональности k служит для приведения статистической механической энтропии к классической термодинамической энтропии Клаузиуса: Вместо этого можно было бы выбрать масштабированную безразмерную энтропию в микроскопических терминах так, чтобы Тепловое напряжениеИсторияВ 1920 году Планк написал в своей лекции о присуждении Нобелевской премии :
В версиях СИ до переопределения базовых единиц СИ в 2019 году постоянная Больцмана была измеренной величиной, а не фиксированным значением. Его точное определение также менялось на протяжении многих лет из-за переопределения кельвина (см. Кельвин § История ) и других базовых единиц СИ (см. Джоуль § История ). Стоимость в разных единицахНатуральные единицыТогда формула равнораспределения энергии, связанной с каждой классической степенью свободы, принимает вид E d о ж знак равно 1 2 Т <\ Displaystyle E _ <\ mathrm Использование натуральных единиц упрощает многие физические отношения; в этой форме определение термодинамической энтропии совпадает с формой информационной энтропии :
| |