что такое порядок фильтра

Что такое порядок фильтра

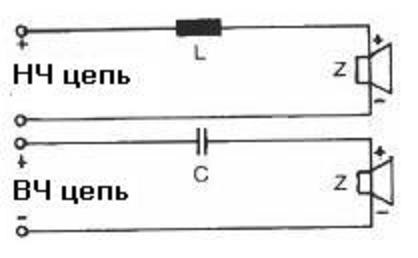
Вспомним школьный курс физики. Основное свойство катушки индуктивности заключается в том, что она сопротивляется быстрым изменениям протекающего через нее тока. Иными словами, на низких частотах ее сопротивление маленькое, а с ростом частоты оно заметно растет. Если включить её последовательно с динамиком, она пропустит на него низкие частоты, но ослабит высокие, и мы получим самый настоящий фильтр нижних частот.

А вот у конденсатора свойства прямо противоположные – он вообще не пропускает через себя постоянный ток, но зато может пропускать переменный. Причем чем выше частота сигнала, тем меньшее сопротивление он ему будет оказывать. Так что если мы включим конденсатор последовательно с твитером, то получим ФВЧ, который ослабит низкие частоты, зато легко пропустит высокие.

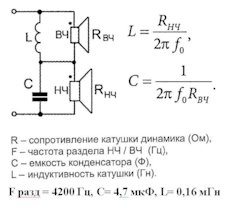
Каждый из таких фильтров будет состоять из одного элемента и назваться они будут фильтрами первого порядка. Они простые в расчете, потому что содержат всего по одному элементу – катушке или конденсатору. Если мы захотим сделать фильтры с определенной частотой среза Fc (она определяется по уровню –3 дБ), то нам нужно будет подобрать катушку и конденсатор вот с такими параметрами (индуктивность в мГн, емкость в мкФ):

где Z – это импедансы динамиков (Ом), которые мы собираемся подключить к фильтрам. Часто в расчетах в качестве Z подставляют номинальные импедансы. В общем-то, так действительно можно в первом приближении оценить, какого примерно порядка нам понадобятся катушка или конденсатор, но не более того. Если требуется точный расчет параметров, то для этого нужно знать саму Z-характеристику динамиков, а в формулу подставлять не номинальные значения импедансов, а значения на конкретной частоте Fc.

Недостаток фильтров первого порядка – невысокая крутизна среза, порядка 6 дБ/октава. Иными словами, они не очень «старательно» фильтруют сигнал, а значит, с такими фильтрами широкий диапазон частот будет воспроизводиться и твитером, и мидбасовым динамиком одновременно.

Это плохо из-за того, что динамики, как правило, разносятся в автомобиле на довольно приличное расстояние друг от друга. В результате до ушей будет доходить не то, что они излучают, а некий результат сложения, интерференции. Ну а то, что разные динамики не могут воспроизводить один и тот же сигнал абсолютно одинаково, только усугубляет ситуацию.

Чтобы избавиться от этого недостатка и уменьшить диапазон совместной работы динамиков, применяют фильтры более высоких порядков. Например, если добавить к фильтрам первого порядка еще по одному элементу, то получим уже фильтр второго порядка.

Такой фильтр даёт более крутой спад АЧХ за пределами зоны пропускания, отсюда и более узкая полоса совместной работы.

При дальнейшем добавлении элементов по тому же принципу можно получить фильтры третьего, четвертого и еще выше порядков. Они будут еще лучше справляться с фильтрацией.

И всё бы хорошо, но любые фильтры имеют одну неприятную особенность – они сдвигают сигнал по фазе, задерживают его. На первый взгляд, ничего страшного в этом нет, ведь, к примеру, звуковые процессоры тоже задерживают сигнал. Но дело в том, что процессоры задерживают сигнал «целиком», а у фильтров эта задержка разная на разных частотах. А что получится, если мы в широкополосном музыкальном сигнале одни частоты задержим сильнее других? Форма сигнала, понятное дело, исказится. Такие искажения называются фазовыми. И чем выше порядки фильтров, тем больше эта фазовая неравномерность. Я ни в коем случае не призываю отказываться от фильтров высоких порядков, но к ним лучше относиться с осторожностью.

Источник

Фильтры первого и второго порядка.

Для разделения пищалок и мидбасов по частотам дабы не перегрузить динамики и отсечь не нужные для воспроизведения частоты используют фильтры.

Фильтры бывают различных порядков (первого, второго, третьего…). Рассмотрим самый доступные это фильтр первого порядка и второго порядка.

Фильтр первого порядка.

Для подбора компонентов существует таблица номиналов.

Фильтр первого порядка позволяет отсечь мидбас от пищалки на желаемой частоте раздела к примеру 4000 Гц. При этом мидбас будет играть в нижней части до 4000 Гц, а пищалка в верхней. Крутизна спада (затухания сигнала) для такого фильтра всего лишь 6 дБ/окт. При использовании такого фильтра возникает сдвиг фаз 90 градусов. Которые потребуют коррекции либо смещением компонентов, либо необходима коррекция при помощи временных задержек.

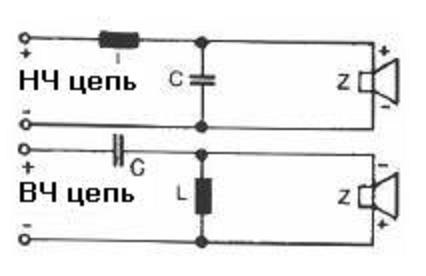
Фильтр второго порядка.

Крутизна спада для такого фильтра 12 дБ/окт. При использовании такого фильтра возникает сдвиг фаз 180 градусов. Которые потребуют коррекции, как вариант это смена полярности динамиков.

Спасибо что дочитали! Всем добра и ровных дорог! Да прибудет с вами автозвук! Если считаете данную запись полезной нажмите поделиться.

Комментарии 22

Приветствую! Скажи пожалуйста, т.е чтобы динамик нч играл до 100гц а потом плавно затухал — достаточно катушки 6,4мГ (миллиГенри?), верно?

Не сильно понятно присутствие на НЧ индуктивности. В параллельном фильтре первого порядка. Я понял бы если бы НЧ был широкополосник. Ну и по мимо фильтров надо учитывать чувствительность НЧ и ВЧ, и добавлять сопротивление на ВЧ головку т.к. у них чувствительность обычно за 100.
Лучше использовать последовательный фильтр первого порядка, а не параллельный, чтобы не получить ужас из АЧХ.
Аудиофилы называют любителей автозвука родственниками с колхоза.

Лучше всего, если позволяет бюджет, строить поканалку, с фильтрацией каждого отдельно канала через процессор) А если бюджет поет романсы, то пилим фильтры, методом подбора)

Не финансы должны быть. Мозги.
Сейчас продаются куча разных компонентов — транзисторы, резисторы и другая прибулда. Очень не дорого.
Куча калькуляторов в интернете.
Паяльник в руки и вперёд.

Не сильно понятно присутствие на НЧ индуктивности. В параллельном фильтре первого порядка. Я понял бы если бы НЧ был широкополосник. Ну и по мимо фильтров надо учитывать чувствительность НЧ и ВЧ, и добавлять сопротивление на ВЧ головку т.к. у них чувствительность обычно за 100.
Лучше использовать последовательный фильтр первого порядка, а не параллельный, чтобы не получить ужас из АЧХ.
Аудиофилы называют любителей автозвука родственниками с колхоза.

Такая схема подключения (последовательная) натуральное ОВНО!
Я её уже строил 30 лет назад, когда в школе учился.

Здравствуйте. это МикроФарад и МикроГенри (или милли)?

В таблице представлены номиналы ёмкости и индуктивности, я правильно понимаю на вч и нч одни и те же номиналы, только схема подключения разная?

нашел калькулятор для фильтра НЧ
нашел в Красноярске где купить катушку индуктивности и конденсатор… и подставил их параметры в калькулятор
получилось вот что:
(параметры которые можно изменить это индуктивность и емкость)

Индуктивность катушки L1 10 микрогенри мкГн µH
Ёмкость конденсатора С1 2200 микрофарад мкФ µF
получилось:
Частота среза фильтра Fср 1517.48 Гц
Характеристическое сопротивление 0.07 Ом

Даров. У меня саб босэ без усилка. Хочу сделать фильтр только для низких частот что нужно сделать. Транзистор на 133 микрофорат?

Привет, смотри ответ ниже.

Подсчитай сам вот ссылка на калькулятор www.aie.sp.ru/Calculator_filter.html

Привет всем подскажите как правильно подобрать фильтры? Хочу сделать чтобы овалы играли только бас. А в дверях средина и высокие. Авто седан ставить в багажник саб пока не вижу смысла. Маг обычный не процессорный. Всем спасибо за помощь)

Привет, можно катушки намотать и будет тебе фильтр первого порядка, можно еще конденсатор подцепить и будет фильтр второго, срез круче получается. А так в идеале купить магнитолу линейки 100 от пионер, а они уже умеют резать. Там режим сабвуфера есть, т.е. блины подключенные на тыловой канал будут как саб работать.

привет, подскажи на схеме С-это конденсатор а L-?

Источник

Опции темы

Поиск по теме

Отображение

Кроссоверы— это устройства в звуковых системах, которые создают нужные рабочие частотные диапазоны для динамиков. Динамики сконструированы таким образом, чтобы работать в определенном частотном диапазоне. Они не приемлют частоты, не входящие в эти рамки. Если на высокочастотный динамик (твитер) подать низкую частоту, то звуковая картина испортится, а если сигнал еще и мощный, то твитер «сгорит». Высокочастотные динамики должны работать только с высокими частотами, а низкочастотные динамики должны получить от общего звукового сигнала только низкочастотный диапазон. Оставшаяся средняя полоса достается среднечастотным динамикам (мидвуферы). Следовательно, задача кроссоверов заключается в разделении звукового сигнала на нужные (оптимальные) частотные полосы для соответствующих типов динамиков.

Кроссоверы четвертого порядка. Кроссоверы Баттерворта четвертого порядка имеют высокую чувствительность равную 24 дБ на октаву, что резко уменьшает взаимовлияние динамиков в области разделения частот. Сдвиг по фазе составляет 360 градусов, что фактически означает его отсутствие. Однако величина фазового сдвига в данном случае непостоянна и может привести к неустойчивой работе кроссовера. Эти кроссоверы практически не применяются на практике.
Оптимизировать конструкцию кроссовера четвертого порядка удалось Линквицу и Рили. Данный кроссовер состоит из двух последовательно соединенных кроссоверов Баттерворта второго порядка для твитера, и тоже самое для басового динамика. Чувствительность их также равна 24 дБ на октаву, однако уровень выходного сигнала на каждом фильтре меньше на 6 дБ, чем уровень выходного сигнала кроссовера. Кроссовер Линквица-Рили не имет фазовых сдвигов и позволяет проводить временную коррекцию для динамиков, не работающих в одной физической плоскости. Эти кроссоверы по сравнению с другими конструкциями дают самые лучшие акустические характеристики.

Конструирование пассивных кроссоверов

Пассивные и активные кроссоверы

Настройка активного кроссовера

В этой таблице приведены начальные величины частот среза для различных типов динамиков при настройке активных кроссоверов.

Источник

Симметричные НЧ-ВЧ фильтры

В задачах обработки сигналов часто возникает необходимость фильтрации сигналов, когда сигнал разбивается на узкополосные диапазоны. В бытовом плане мы с этим сталкиваемся при воспроизведении музыки через акустические системы, в которых каждый громкоговоритель (динамик) воспроизводит свою полосу частот, которых обычно три — низкие (НЧ), средние (СЧ) и высокие (ВЧ); для воспроизведения сверхнизких частот иногда выделяют отдельную акустическую систему под названием «сабвуфер». Конкретные границы частот зависят от реализации и ориентировочно находятся на границах 100 Гц, 1 кГц и 5 кГц. Для того, чтобы не было резких скачков громкости между динамиками, используют частичное перекрытие — когда амплитуда воспроизводимой полосы частот плавно спадает на одном, одновременно нарастая на другом.

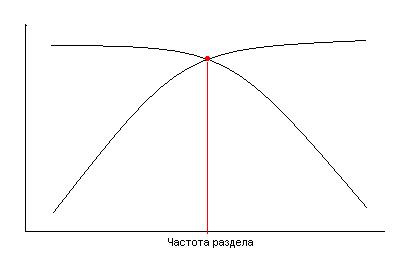
Наиболее популярными фильтрами для такого разбиения являются фильтры Линквитца-Рейли 4-го порядка, представляющих из себя два последовательно соединённых фильтра Баттерворта, изображение АЧХ которых многим хорошо знакомо:

Популярность их обусловлена простотой схемотехнической реализации и гладкой АЧХ с отсутствием пульсаций. Порядок фильтра, обуславливающий скорость затухания, обычно выбирают 4-ым.

У всех аналоговых фильтров есть недостатки — нестабильность параметров и сложность в настройке. Другой немаловажным недостатком является неустранимый сдвиг фаз. Реализовать фазолинейный фильтр в аналоге невозможно, потому что это нарушает причинно-следственную связь выходного сигнала от входного.

Появление цифровой техники в целом и цифровых источников сигналов в частности позволило избавиться от недостатков аналоговых фильтров путём реализации их непосредственно программным образом, в цифре. Такой подход требует «мультиампинг» — когда используется отдельный усилитель мощности для каждой полосы частот — в отличие от классического подхода, когда сначала усиливается широкополосный сигнал, который разбивается на частотные полосы (обычно) пассивными фильтрами. Применение нескольких усилителей вместо одного очевидным образом удорожает технику, поэтому такое решение выбирают для особо качественных систем.

▍ Краткое введение в цифровые фильтры

Цифровой фильтр — это функция, которую можно рассматривать как во временной, так и в частотной области. Во временной области она определяет импульсную характеристику, получаемой при реакции некоторого устройства или его мат. модели на единичный импульс (на слух воспринимаемый как щелчок). В частотной области она определяет затухание или усиление амплитуды и сдвиг фазы на отдельно взятой частоте. Переход между этими областями (в англоязычной литературе используется слово domain) осуществляется через преобразование Фурье, которое между функциями во временной и в частотной области задаёт однозначное соответствие.

Разделяют два типа цифровых фильтров:

IIR (Infinite Impulse Response) — фильтры с бесконечной импульсной характеристикой. По сути, представляют собой всё те же аналоговые фильтры, но «моделируемые» в цифре — математический аппарат в обоих случаях идентичен (в основе которого лежит преобразование Лапласа). Отсюда следует бесконечность импульсной характеристики, которую можно представить в виде суммы экспоненциально затухающих синусоид.

Вот так выглядит (обрезанная справа) импульсная характеристика рекурсивного фильтра низких частот с высокой добротностью

Их преимуществом является низкая вычислительная сложность — каждое новое значение вычисляется рекурсивно в зависимости от предыдущих. Они также чувствительны к погрешностям вычисления и ошибкам округления — поэтому вопрос устойчивости (гарантированного затухания при отсутствии сигнала на входе) таких фильтров в теории рассматривается отдельно.

Наиболее простым является фильтр низких частот первого порядка:

FIR (Finite Impulse Response) — фильтры с конечной импульсной характеристикой. Самый известный фильтр такого рода — это скользящее среднее, а сама фильтрация осуществляется посредством линейной свёртки отсчётов фильтра с отсчётами входного сигнала. Здесь сложность уже квадратичная — однако её можно уменьшить до , если использовать алгоритм быстрой свёртки с использованием быстрого преобразования Фурье (FFT). Конечность количества отсчётов накладывает свои ограничения на форму АЧХ, приводя к пульсациям.

А так выглядит импульсная характеристика фазолинейного FIR-фильтра низких частот

Довольно популярной практикой при проектировании фильтров является линеаризация — когда берётся АЧХ известного IIR фильтра и формируется из неё FIR с линейной фазой.

▍ Постановка задачи

Итак, нашей задачей является сформировать пару фильтров, делящих полосу частот на две с перекрытием. При этом они должны обладать следующими характеристиками:

Cимметричность (зеркальность) АЧХ решает две задачи:
1) ВЧ-составляющую сигнала можно получить вычитанием из исходного НЧ-составляющей — как в частотной, так и во временной области;
2) избавляет от мучительного выбора, для какого фильтра — НЧ или ВЧ — предпочтительнее более пологий или крутой спад АЧХ.

Похожее требование есть у квадратурных зеркальных фильтров, в которых задаётся симметрия в линейном масштабе частот. Но нас интересует именно логарифмический масштаб, как более естественный для человеческого слуха.

▍ Общий алгоритм построения

Существует несколько подходов к проектированию КИХ-фильтров, из которых наиболее простым и интуитивно-понятным является следующий:

▍ Аналитическое решение

Озвученным выше требованиям гладкости и симметрии (но не фазолинейности) соответствует фильтр Линквитца-Рейли. Зная формулу АЧХ , где — порядок фильтра, формулу импульсной характеристики можно получить аналитически через интеграл Фурье, а конкретные отсчёты FIR фильтра считать непосредственным её вычислением.

График фильтра в логарифмическом масштабе:

Лучший способ для вычисления интеграла Фурье — это использовать какую-нибудь систему компьютерной алгебры. Например, в Wolfram Mathematica это будет выглядеть так:

InverseFourierTransform[1/(1 + w^2), w, x] // FullSimplify
↓

График получившейся функции, она же импульсная характеристика:

Как видно из формулы и графика, импульсная характеристика бесконечна — стремится к нулю, но не достигает его; а также симметрична относительно нуля (за счёт фазолинейности). Ограничение её во времени осуществляется путём умножения на оконную функцию, за счёт чего значения функции за пределами окна приобретают нулевые значения, не требующих участия в расчётах. Побочным эффектом этого становится искажения исходного спектра фильтра — поскольку при умножении функций их спектры сворачиваются. Итоговый спектр можно увидеть также через преобразование Фурье. Например, для прямоугольного окна получим

в результате чего АЧХ фильтра изменится на

Помножив её на импульсную характеристику фильтра, получим:

Как видно, величина пульсаций значительно уменьшилась. По графику видно, что «полка» фильтра слегка опустилась — в идеале это тоже нужно учитывать и компенсировать. В данном случае она составила (на нулевой частоте):

FourierTransform[E^-Abs[x] Sqrt[Pi/2] NuttallWindow[x/20], x, w] /.w->0.0
↓

Мнимая часть здесь получилась вследствие погрешности при численных вычислениях и её можно смело отбрасывать (об этом говорит значение , поскольку точность вычислений в формате double и представляет примерно 16 десятичных цифр).

Аналогичным образом можно посчитать импульсные характеристики и для более высоких (но только целых) порядков, например:

InverseFourierTransform[1/(1+w^4), w, x] // FullSimplify
↓

Как видно, автоматического упрощения уже недостаточно и здесь требуется ручная работа по приведению формулы к удобочитаемому виду. В итоге получается следующая формула (в комплексных числах) для импульсной характеристики фильтра Линквитца-Рейли произвольного порядка:

При вычислении за счёт сложения комплексно-сопряжённых чисел мнимая часть обнуляется и в результате получится чисто действительная функция. Эту формулу можно выписать и непосредственно в действительных числах:

▍ Переход в дискретную область

Синтез фильтра в дискретном виде осуществляется сходным образом. Принципиальное отличие состоит в том, что:

Также имеются различия (но не результат) при работе с классическим (комплексным) FFT, Real-FFT, который работает только с половиной спектра, предполагая его симметрию, и FHT (быстрое преобразование Хартли), в котором изначально и данные, и спектр определены в поле действительных чисел. Здесь будет использоваться классический FFT.

Итак, определим формулу для фильтра — для примера 4-го порядка:

Выберем частоту дискретизации (в герцах), стандартную для современных ЦАП:

Выберем частоту среза, на которой подавления будет составлять 0.5 (-6 дБ) и соответствовать нормированной частоте w=1:

Выберем размер массива (маленький, для наглядности):

Далее необходимо заполнить массив. Каждому элементу в нём будет соответствовать частота от 0 (постоянная составляющая) до (частота Найквиста), равномерно распределённых в линейном масштабе. Определим функцию, которая в зависимости от индекса будет считать нормированную частоту:

Заполняем первую половину (положительную часть спектра) массива:

Здесь фазу на каждой нечётной частоте мы повернули на 180° для того чтобы после БПФ максимум импульса был расположен по центру массива.

Вторую половину (отрицательную часть спектра) получаем реверсом первой, за исключением крайних частот (нулевой — постоянной составляющей и максимальной — частоты Найквиста, потому что для их описания достаточно одного числа).

spectrumdata =
Join[halfspectrumdata, Reverse[halfspectrumdata[[2;;size/2]]]];

Теперь делаем обратное преобразование Фурье:

И накладываем оконную функцию — Нутталла, как и в прошлый раз:

В качестве заключительного аккорда можно нормировать полку фильтра к единице. Для этого снова потребуется прямое FFT, чтобы узнать значение постоянной составляющей:

Fourier[wavedata][[1]]
↓

и затем просто поделить на него значение каждого отсчёта в импульсе

Сделав FFT ещё раз, можно убедиться, что постоянная составляющая стала равной единице:

Fourier[wavedata][[1]]
↓

Если бы мы проектировали фильтр высоких частот, но нормализацию нужно было бы делать по амплитуде не на нулевой частоте, а на частоте Найквиста.

▍ Кусочно-непрерывные фильтры

Из её графика в линейном масштабе симметрия, обеспечивающая суммирование в единицу, хорошо видна:

А вот в логарифмическом масштабе — уже нет, зато хорошо видно главное отличие от фильтра Линквитца-Рейли — спад не пологий, а имеет выраженную границу справа, за которой громкость (в децибелах) равна минус бесконечности. Дополнение до единицы даёт ВЧ-фильтр (жёлтым цветом), который и обладает желаемой симметрией:

На большем диапазоне громкости это свойство фильтров выглядит ещё более наглядным:

1) через граничные частоты

2) через центральную частоту и ширину (в октавах)

3) через центральную и верхнюю граничную частоту

4) через центральную и нижнюю граничную частоту

Теперь, используя некоторую функцию фильтра, можно получить его импульсную характеристику по вышеописанному алгоритму, который можно определить отдельной функцией:

Передав в эту функцию наш кубический фильтр и окно Нуттала получим

SymmetricFilterImpulseResponse[1000, 0.5, 512, 48000, FilterCubicClip, NuttallWindow]
↓

▍ Несколько интересных фильтр-функций

Помимо уже рассмотренной кубической, можно придумать множество и других функций для фильтров, основанных на какой-нибудь математической идее. Также имеет значение, насколько легко может быть вычислена (и может ли быть вычислена вообще) обратная функция.

Параболическая, наименее вычислительно затратная. При необходимости, обратная к ней функция находится довольно элементарно:

\frac<1> <2>\end \right.$» data-tex=»display»/>

Кубическая. Обратная к ней функция уже немного контринтуитивна (а если вам интересно, откуда здесь взялись тригонометрические функции — тогда сюда):

Используя полином 5-ой степени, с двумя нулевыми производными на границах сопряжения. Обратная функция здесь уже в элементарных функциях не выражается (потому и не приведена):

Используя полином 13-ой степени — с дополнительным «выпрямлением»:

Используя рациональный полином — даёт более гладкую характеристику и более простую обратную функцию, чем у кубической:

С заданным количеством нулевых производных в точках стыковки, частным случаем которой является предыдущая функция. Обратная к ней функция также легко находится:

Линейно спадающая в логарифмическом масштабе:

\frac<1> <2>\end \right.$» data-tex=»display»/>

Более плавный вариант предыдущего с возможностью регулировки «жёсткости». Здесь уже обратная функция для произвольного n в элементарных функциях не выражается:

С бесконечным количеством нулевых производных в точках стыковки, что обеспечивает идеальное сопряжение. А здесь обратная функция легко находится:

С максимально быстро затухающей импульсной характеристикой — что при достаточно больших (5$» data-tex=»inline»/>) позволяет обойтись без оконной функции вообще. Сама формула получена модуляцией аргумента кубической функции, т.е. :

▍ Заключение

Несмотря на очевидность постановки задачи, мне не встречалось ничего подобного ни в специализированных решениях, ни в мат. пакетах общего назначения. Возможно, что это связано с инерцией мышления в стиле «всё, что можно придумать, уже придумано». Однако это не так хотя бы потому, что сейчас доступны технологии и вычислительные мощности, о которых всего лишь 50 лет назад инженеры и математики не могли и мечтать.

В качестве proof of concept фильтры по такой методике были реализованы в плагине для популярного в аудиофильских кругах плеера foobar, извлекающего канал сабвуфера из стереосигнала (официальный репозиторий); и ещё в одном, просто для демонстрации звучания (неофициальный репозиторий). Для реализации таких фильтров в «мультиампинг»-системах можно использовать готовые решения, позволяющие загружать заранее посчитанные импульсные файлы. При отсутствии мат.пакетов их можно посчитать даже в excel-е (используя преобразование Фурье из пакета анализа).

Насколько такие фильтры «звучат» лучше классических решений — вопрос уже аудиофильский, но, как минимум, разницу в звучании обеспечивают вполне объективную и обеспечивают возможность для более точной настройки.

Источник