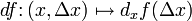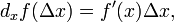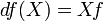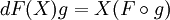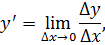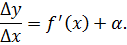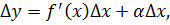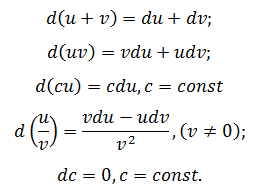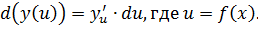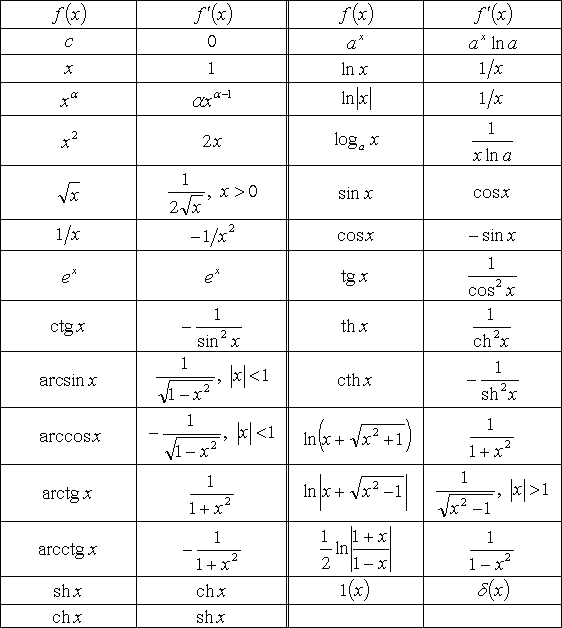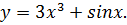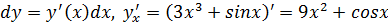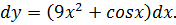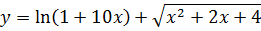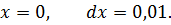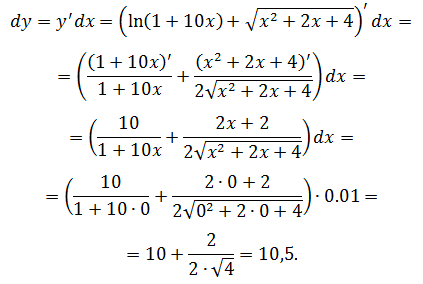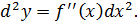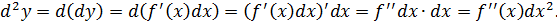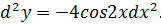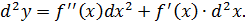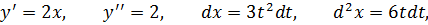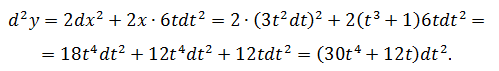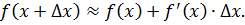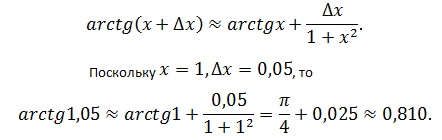что такое полный дифференциал функции

Полный дифференциал

Дифференциа́л в математике — линейная часть приращения функции или отображения. Это понятие тесно связанное с понятием производной по направлению.

Содержание

Неформальное описание

в частности, разность приращения функции и её дифференциала — бесконечно малая величина:

Определения

Для функций

Дифференциал гладкой вещественнозначной функции f определённой на M ( M — область в или гладкое многообразие) представляет собой 1-форму и обычно обозначается df и определяется соотношением

Для отображений

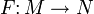
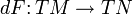
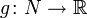
Дифференциал гладкого отображения из гладкого многообразия в многообразие есть отображение между их касательными расслоениями, , такое что для любой гладкой функции имеем

Это понятие естественно обобщает дифференциал функции.

Связанные определения

Свойства

Примеры

История

Термин Дифференциал (от лат. differentia — разность, различие) введён Лейбницем. Изначально, dx применялось для обозначения «бесконечно малой» — величины, которая меньше всякой конечной величины и всё же не равна нулю. Подобный взгляд оказался неудобным в большинстве разделов математики (за исключением нестандартного анализа).

См. также

Полезное

Смотреть что такое «Полный дифференциал» в других словарях:

полный дифференциал — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN ordinary differentialtotal differential … Справочник технического переводчика

Полный дифференциал — функции f (x, у, z. ) нескольких независимых переменных выражение в случае, когда оно отличается от полного приращения (См. Полное приращение) Δf = f (x + Δx, y + Δy, z + Δz,…) f (x, y, z, …) на… … Большая советская энциклопедия

ДИФФЕРЕНЦИАЛ — (лат., от differe различать). Предел бесконечно малой разности между функцией переменного, получившего бесконечно малое приращение, и первоначальной функцией того же переменного (мат. терм.). Словарь иностранных слов, вошедших в состав русского… … Словарь иностранных слов русского языка

Дифференциал (механика) — У этого термина существуют и другие значения, см. Дифференциал (значения). Устройство дифференциала (центральная часть) Дифференциал это механическое устройство, котор … Википедия

Дифференциал (автомобиль) — Устройство дифференциала(центральная часть) Дифференциал это механическое устройство, которое передает вращение с одного источника на два независимых потребителя таким образом, что угловые скорости вращения источника и обоих потребителей могут… … Википедия

Полный привод — У этого термина существуют и другие значения, см. Полный привод (значения). Наиболее распространённая (но не единственная) схема трансмиссии полноприводного автомобиля. Полный привод (4×4, 4WD … Википедия

Постоянный полный привод — Наиболее распространённая (но не единственная) схема трансмиссии полноприводного автомобиля. Полный привод (4×4, 4WD, AWD) конструкция трансмиссии автомобиля, когда крутящий момент, создаваемый двигателем, передаётся на все колеса. До… … Википедия

Теплота — 1) Т. мы называем причину, вызывающую в нас специфические, всем известные тепловые ощущения. Источником этих ощущений являются всегда какие либо тела внешнего мира, и, объективируя наши впечатления, мы приписываем этим телам содержание некоторого … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Источник

Дифференциал функции определение, виды, свойства, формула полного дифференциала функции, геометрический смысл, правило применения, примеры решения уравнений

При выполнении некоторых расчётов в исследованиях, проектировании, анализе полученных опытных путём данных часто возникает необходимость предварительной прикидки результата, которую удобно выполнять, используя дифференциал функции.

Приближённые вычисления, выполненные с его помощью, могут дать новые направления дальнейшего изучения объектов и их разработок.

Понятие и геометрический смысл дифференциала

Пусть y = f (x) имеет производную

Применяя свойства предела функции, получают равенство

После умножения обеих частей на приращение аргумента Δx, образуется тождество:

в котором в правой части записано слагаемое, являющееся бесконечно малой одного порядка с Δx, далее идет слагаемое более высокого порядка.

Определение 1

Дифференциалом функции y = f (x) первого порядка называется главная часть её приращения f′(x)Δx, которую обозначают dy (или d(f(x)).

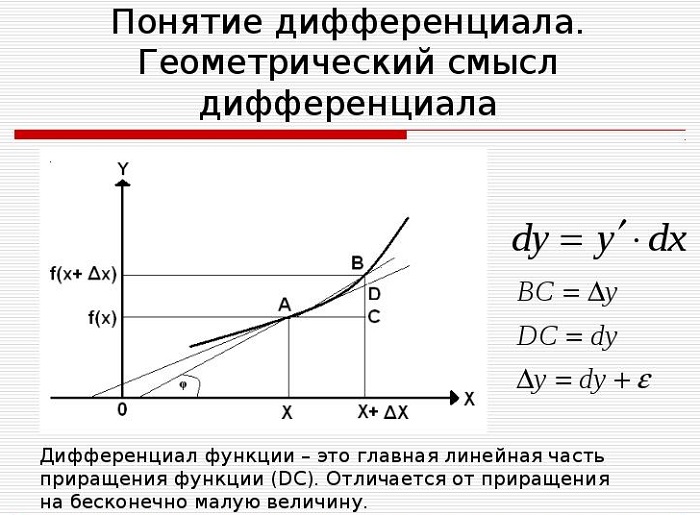
Для наглядного представления и понимания определения рассматривается касательная к графику функции y = f(x) в точке x. Когда значение переменной сдвигается по построенной прямой (получает приращение) на некоторую малую величину Δx, значение второй координаты точки тоже меняется.

Значит, дифференциал функции y = f(x) в точке x равен приращению ординаты касательной, когда её абсцисса меняется на величину Δx.

Определение 2

Дифференциал от дифференциала называется дифференциалом второго порядка. Таким же рекуррентным образом вводятся понятия дифференциалов более высоких порядков.

Формы записи дифференциала

Для нахождения дифференциала независимой переменной рассматривают функцию y = x, учитывая, что x’ = 1, а, следовательно:

Отсюда получается формула:

Для второго порядка вводится обозначение d 2 y.

Свойства дифференциала

Существующая таблица производных помогает выделить некоторые свойства дифференциалов, например, для суммы, произведения, частного получаются следующие правила:

Одним из важных свойств является инвариантность (неизменность) формы записи, независимо от того, является ли функция элементарной или композицией элементарных (сложной). Фактически,

Примеры решения задач

Задача №1

Найти дифференциал функции

Задача №2

Вычислить значение дифференциала функции

В помощь студентам создан онлайн калькулятор, который позволяет ввести функцию, нажать кнопку и получить форму или значение дифференциала.

Если dx есть константа, то для высших порядков имеет место следующая формула:

Этот результат вытекает непосредственно из определения:

Задача №3

Найти d 2 y, если y = cos2x и x – независимая переменная.

Если x – функция от некоторой другой независимой переменной, то свойство инвариантности перестаёт работать, следовательно,

Задача №4

Найти d 2 y, если y = x 2 и x = t 3 + 1, t – независимый аргумент.

Нетрудно заметить, что если выразить y напрямую через t, то получится тот же результат.

с высокой степенью точности можно вычислить приращение любой дифференцируемой зависимости.

Раскрыв Δy, сделав соответствующие преобразования, приходят к формуле приближённых вычислений:

Задача №5

Вычислить приближённо arctg1,05.

Пусть f(x) = arctg x. Тогда

Полный дифференциал функции

Математика не ограничивается множеством функций одного независимого аргумента. Рассматриваются зависимости от двух и более переменных.

Определения похожи, отличается вид главной части. Рассматриваются несколько слагаемых.

Например, если z = f(x;y) то

Последнее равенство есть формула полного дифференциала. Для функции нескольких переменных сохраняется принцип построения.

Если рассматривают приращения только по одной переменной, то приходят к понятию частных дифференциалов.

Заключение

Высшая математика позволяет находить приближённо общий корень системы уравнений, пользуясь дифференциальным исчислением, делать прикидку результатов, прогнозировать получаемое.

Источник

При выполнении некоторых расчётов в исследованиях, проектировании, анализе полученных опытных путём данных часто возникает необходимость предварительной прикидки результата, которую удобно выполнять, используя дифференциал функции. Приближённые вычисления, выполненные с его помощью, могут дать новые направления дальнейшего изучения объектов и их разработок.

Понятие и геометрический смысл дифференциала

Пусть y = f (x) имеет производную

Применяя свойства предела функции, получают равенство

После умножения обеих частей на приращение аргумента Δx, образуется тождество:

в котором в правой части записано слагаемое, являющееся бесконечно малой одного порядка с Δx, далее идет слагаемое более высокого порядка.

Определение 1

Дифференциалом функции y = f (x) первого порядка называется главная часть её приращения f′(x)Δx, которую обозначают dy (или d(f(x)).

Для наглядного представления и понимания определения рассматривается касательная к графику функции y = f(x) в точке x. Когда значение переменной сдвигается по построенной прямой (получает приращение) на некоторую малую величину Δx, значение второй координаты точки тоже меняется.

Значит, дифференциал функции y = f(x) в точке x равен приращению ординаты касательной, когда её абсцисса меняется на величину Δx.

Определение 2

Дифференциал от дифференциала называется дифференциалом второго порядка. Таким же рекуррентным образом вводятся понятия дифференциалов более высоких порядков.

Формы записи дифференциала

Для нахождения дифференциала независимой переменной рассматривают функцию y = x, учитывая, что x’ = 1, а, следовательно:

Отсюда получается формула:

Для второго порядка вводится обозначение d 2 y.

Свойства дифференциала

Существующая таблица производных помогает выделить некоторые свойства дифференциалов, например, для суммы, произведения, частного получаются следующие правила:

Одним из важных свойств является инвариантность (неизменность) формы записи, независимо от того, является ли функция элементарной или композицией элементарных (сложной). Фактически,

Примеры решения задач

Задача №1

Найти дифференциал функции

Задача №2

Вычислить значение дифференциала функции

В помощь студентам создан онлайн калькулятор, который позволяет ввести функцию, нажать кнопку и получить форму или значение дифференциала.

Если dx есть константа, то для высших порядков имеет место следующая формула:

Этот результат вытекает непосредственно из определения:

Задача №3

Найти d 2 y, если y = cos2x и x – независимая переменная.

Если x – функция от некоторой другой независимой переменной, то свойство инвариантности перестаёт работать, следовательно,

Задача №4

Найти d 2 y, если y = x 2 и x = t 3 + 1, t – независимый аргумент.

Нетрудно заметить, что если выразить y напрямую через t, то получится тот же результат.

с высокой степенью точности можно вычислить приращение любой дифференцируемой зависимости.

Раскрыв Δy, сделав соответствующие преобразования, приходят к формуле приближённых вычислений:

Задача №5

Вычислить приближённо arctg1,05.

Пусть f(x) = arctg x. Тогда

Полный дифференциал функции

Математика не ограничивается множеством функций одного независимого аргумента. Рассматриваются зависимости от двух и более переменных.

Определения похожи, отличается вид главной части. Рассматриваются несколько слагаемых.

Например, если z = f(x;y) то

Последнее равенство есть формула полного дифференциала. Для функции нескольких переменных сохраняется принцип построения.

Если рассматривают приращения только по одной переменной, то приходят к понятию частных дифференциалов.

Заключение

Высшая математика позволяет находить приближённо общий корень системы уравнений, пользуясь дифференциальным исчислением, делать прикидку результатов, прогнозировать получаемое.

Источник

Как найти полный дифференциал функции?

При выполнении некоторых расчётов в исследованиях, проектировании, анализе полученных опытных путём данных часто возникает необходимость предварительной прикидки результата, которую удобно выполнять, используя дифференциал функции.

Приближённые вычисления, выполненные с его помощью, могут дать новые направления дальнейшего изучения объектов и их разработок.

Понятие и геометрический смысл дифференциала

Пусть y = f (x) имеет производную не равную нулю.

Применяя свойства предела функции, получают равенство.

После умножения обеих частей на приращение аргумента Δx, образуется тождество:

в котором в правой части записано слагаемое, являющееся бесконечно малой одного порядка с Δx, далее идет слагаемое более высокого порядка.

Определение 1

Дифференциалом функции y = f (x) первого порядка называется главная часть её приращения f′(x)Δx, которую обозначают dy (или d(f(x)). Для наглядного представления и понимания определения рассматривается касательная к графику функции y = f(x) в точке x.

Когда значение переменной сдвигается по построенной прямой (получает приращение) на некоторую малую величину Δx, значение второй координаты точки тоже меняется.

Значит, дифференциал функции y = f(x) в точке x равен приращению ординаты касательной, когда её абсцисса меняется на величину Δx.

Определение 2

Дифференциал от дифференциала называется дифференциалом второго порядка. Таким же рекуррентным образом вводятся понятия дифференциалов более высоких порядков.

Формы записи дифференциала

Для нахождения дифференциала независимой переменной рассматривают функцию y = x, учитывая, что x’ = 1, а, следовательно:

Отсюда получается формула:

Для второго порядка вводится обозначение d2y.

Свойства дифференциала

Существующая таблица производных помогает выделить некоторые свойства дифференциалов, например, для суммы, произведения, частного получаются следующие правила:

Одним из важных свойств является инвариантность (неизменность) формы записи, независимо от того, является ли функция элементарной или композицией элементарных (сложной). Фактически:

Полный дифференциал функции

Математика не ограничивается множеством функций одного независимого аргумента. Рассматриваются зависимости от двух и более переменных.

Определения похожи, отличается вид главной части. Рассматриваются несколько слагаемых. Например, если z = f(x;y) то

Последнее равенство есть формула полного дифференциала. Для функции нескольких переменных сохраняется принцип построения.

Если рассматривают приращения только по одной переменной, то приходят к понятию частных дифференциалов.

Высшая математика позволяет находить приближённо общий корень системы уравнений, пользуясь дифференциальным исчислением, делать прикидку результатов, прогнозировать получаемое.

Дифференциальные уравнения в полных дифференциалах

Дифференциальным уравнением в полных дифференциалах называется уравнение вида:

Обозначим неизвестную функцию двух переменных (её-то и требуется найти при решении уравнений в полных дифференциалах) через F и скоро вернёмся к ней. Первое, на что следует обратить внимание: в правой части уравнения обязательно должен быть нуль, а знак, соединяющий два члена в левой части, должен быть плюсом.

Второе — должно соблюдаться некоторое равенство, которое является подтверждением того, что данное дифференциальное уравнение является уравнением в полных дифференциалах.

Эта проверка является обязательной частью алгоритма решения уравнений в полных дифференциалах (он во втором параграфе этого урока), так процесс поиска функции F достаточно трудоёмкий и важно на начальном этапе убедиться в том, что мы не потратим время зря.

Итак, неизвестную функцию, которую требуется найти, обозначили через F. Сумма частных дифференциалов по всем независимым переменным даёт полный дифференциал. Следовательно, если уравнение является уравнением в полных дифференциалах, левая часть уравнения представляет собой сумму частных дифференциалов. Тогда по определению:

Вспоминаем формулу вычисления полного дифференциала функции двух переменных:

Решая два последних равенства, можем записать:

Первое равенство дифференцируем по переменной «игрек», второе — по переменной «икс»:

Так как, получим, что является условием того, что данное дифференциальное уравнение действительно представляет собой уравнение в полных дифференциалах.

Алгоритм решения дифференциальных уравнений в полных дифференциалах

Шаг 2. Записать систему уравнений из частных производных, составляющих функцию F:

Шаг 3. Проинтегрировать первое уравнение системы — по x (y остаётся константой и выносится за знак интеграла). Таким образом восстанавливаем функцию F:

, где — пока неизвестная функция от y.

Альтернативный вариант (если так интеграл найти проще) — проинтегрировать второе уравнение системы — по y (x остаётся константой и выносится за знак интеграла). Таким образом так же восстанавливается функция F:

, где — пока неизвестная функция от х.

Шаг 4. Результат шага 3 (найденный общий интеграл) продифференцировать по y (в альтернативном варианте — по x) и приравнять ко второму уравнению системы:

а в альтернативном варианте — к первому уравнению системы:

Из полученного уравнения определяем (в альтернативном варианте ).

Шаг 5. Результат шага 4 интегрировать и найти (в альтернативном варианте найти ).

Шаг 6. Результат шага 5 подставить в результат шага 3 — в восстановленную частным интегрированием функцию F. Произвольную постоянную C чаще записывают после знака равенства — в правой части уравнения. Таким образом получаем общее решение дифференциального уравнения в полных дифференциалах. Оно, как уже говорилось, имеет вид F(x, y) = C.

Источник