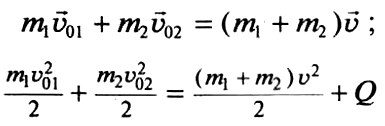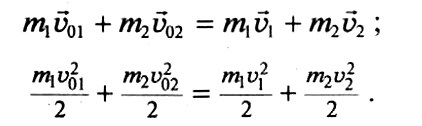что такое полная энергия системы

Полная механическая энергия

Вы будете перенаправлены на Автор24

Энергия в физике означает действие, силу, деятельность. Она представляет скалярную физическую величину, представляющую единую меру разных форм взаимодействия и движения материи, меру превращения одной формы в другую.

Введение понятия энергии в физике удобно, поскольку при условии замкнутости системы, ее энергия будет сохраняться в данной системе все время, на протяжении которого она будет замкнутой. Данное утверждение получило название закона сохранения энергии.

Определение полной механической энергии

Полная механическая энергия в физике характеризуется суммой кинетической и потенциальной энергии, присутствующих в компонентах механической системы. Этот вид энергии связан с движением объектов или его определенным положением, его способностью совершать механическую работу.

Классификация энергии по разным видам зачастую соответствует границам областей изучения в естественных науках. Существуют следующие виды энергии:

Кинетическая и потенциальная энергии

Полную механическую энергию составляют два вида энергии: потенциальная и кинетическая.

Кинетическая энергия представляет энергию механической системы, зависящую от скоростей движения точек. Зачастую выделяют 2 типа энергии: вращательного и поступательного движения. Единицей измерения выступает джоуль.

В более строгом формате, кинетическая энергия представляет разность полной энергии системы и ее энергии покоя. Кинетическая энергия, таким образом, представляет часть полной энергии, обусловленной движением.

Готовые работы на аналогичную тему

Потенциальная энергия представляет скалярную физическую величину, характеризующую запас энергии некоторого тела (материальной точки), которое находится в потенциальном силовом поле. Данный запас энергии идет на приобретение (или изменение) кинетической энергии тела с помощью работы сил поля.

Согласно еще одному определению, потенциальная энергия представляет функцию координат, которая является слагаемым в лагранжиане системы и описывает взаимодействие ее элементов.

Сам термин «потенциальная энергия» ввел в 19 в. шотландский физик У. Рэнкин. Потенциальная энергия принимает нулевое значение для определенной конфигурации тел в пространстве. Выбор этой конфигурации определяется удобством последующих вычислений. Процесс выбора конфигурации называют нормировкой потенциальной энергии.

Закон сохранения энергии

Закон сохранения энергии в физике представляет фундаментальный закон природы, эмпирически установленный. Этот закон заключается в том, что относительно изолированной физической системы можно ввести скалярную физическую величину, представляющую функцию параметров системы и называемую энергией сохранения во времени.

Закон сохранения энергии не относится к конкретным величинам и явлениям, а выражает общую закономерность, его также называют принципом сохранения энергии.

Согласно теореме Нётер, закон сохранения энергии представляет следствие однородности времени (независимости законов физики от момента времени, в который данная система рассматривается).

Допускается переход энергии из одного вида в другой. При этом полная энергия системы, представляющая сумму отдельных видов энергий, будет сохраняться. Для каждого типа энергии закон сохранения может быть сформулирован индивидуально.

Закон сохранения энергии с математической точки зрения будет эквивалентным утверждению: система дифференциальных уравнений, описывающих динамику этой физической системы, имеет первый интеграл движения, связанный с симметричностью уравнений относительно времени.

В теореме Нетер раскрывается фундаментальный смысл закона сохранения энергии. Согласно данной теореме, каждый закон сохранения будет однозначно соответствовать определенной симметрии описывающих физическую систему уравнений.

Вывод этого утверждения сформирован в физике на основании лагранжева формализма. При условии однородности времени, функция Лагранжа, описывающая систему, не зависит от времени. Тогда полная ее производная во времени имеет следующий вид:

Рисунок 1. Функция Лагранжа. Автор24 — интернет-биржа студенческих работ

В механике Ньютона сформулирован частный случай закона сохранения энергии. Закон сохранения механической энергии звучит таким образом: полная механическая энергия для замкнутой системы тел, между которыми действуют исключительно консервативные силы, остается постоянной. Если отсутствуют диссипативные силы (например, силы трения), механическая энергия из ничего не возникнет и в никуда исчезать не может.

В качестве классического примера подтверждения этого утверждения можно рассмотреть математический или пружинный маятники. При наблюдении за пружинным маятником, потенциальная энергия деформированной пружины переходит в кинетическую энергию груза. В случае изучения поведения математического маятника, мы наблюдаем, что аналогично поведет себя в поле силы тяжести потенциальная энергия груза.

Закон сохранения механической энергии выводится из второго закона Ньютона. При учете, что в консервативной системе все силы, воздействующие на тело, потенциальны, их можно представить в виде:

Рисунок 2. Закон сохранения механической энергии. Автор24 — интернет-биржа студенческих работ

Рисунок 3. Потенциальная энергия материальной точки. Автор24 — интернет-биржа студенческих работ

– будет потенциальной энергией материальной точки.

Источник

Механическая энергия, полная механическая энергия

Вы будете перенаправлены на Автор24

Понятие энергии для физики является базовым. Нам известно, что закон сохранения энергии – это фундаментальный закон природы. Он служит основанием для пояснения множества явлений механики, термодинамики, электричества и других физических разделов.

Понятие энергии используется при исследовании задач техники, поскольку самая важная техническая проблема – это проблема генерации, передачи и использования энергии.

Механической энергией считают сумму потенциальной и кинетической энергии. Это энергия, которую связывают с перемещением тел, их расположением, возможностью выполнять работу, взаимодействовать.

Полная энергия тела

Самое общее понятие энергии получают из представлений теории относительности Эйнштейна.

Полной энергией тела ($E$) называют физическую величину, равную произведению релятивистской массы тела ($m$) на скорость света ($c$) в квадрате:

Минимальную энергию имеет тело в той системе отсчета, по отношению к которой оно покоится.

Энергию тела называют энергией покоя ($E_0$), если относительно рассматриваемо системы отсчета тело находится в покое.

Кинетическая энергия

Кинетическую энергию тела можно определить как разность полной энергии и энергии покоя тела:

Кинетическая энергия зависит от скорости перемещения тела по отношению к избранной системе отсчета.

Принимая во внимание выражение (2), формулу (4) преобразуем к виду:

Готовые работы на аналогичную тему

Кинетическая энергия в классической механике

в этом случае для вычисления кинетической энергии мы имеем простую формулу:

Выражение (7) является приближенным, однако, при скоростях с которыми мы имеем дело в обыденной жизни, она дает достаточную точность. Даже, если скорость тела будет несколько сотен метров в секунду, результаты вычисления кинетической энергии при помощи формулы (7) отличны от точных (формула (6)) меньше, чем на десятитысячную часть процента.

Если скорость тела значительно меньше скорости света, кинетическая энергия будет существенно меньше энергии покоя:

Кинетическая энергия протонов в синхрофазотроне в 30 раз больше энергии их покоя.

Для ультра релятивистских скоростей можно считать, что:

Кинетическая энергия – это часть полной энергии тела, которая связана с его движением.

Изменение кинетической энергии будет равно работе ($A$), которую выполняют силы, которые действуют на тело:

Потенциальная энергия

При описании взаимодействия тел при помощи сил в истории использовались две концепции:

Обе концепции присутствовали в науке достаточно долгое время. Для описания гравитационного взаимодействия с позиций близкодействия было введено понятие поля силы. При помощи понятия силового поля, взаимодействие тел на расстоянии определяется так:

Потенциальным полем называют силовое поле, которое выражается при помощи скалярной потенциальной функции ($U(x,y,z,t)$), зависящей от пространственных координат и времени. Данную функцию называют потенциальной. При этом сила, оказывающая воздействие на частицу и потенциальная функция связаны соотношением:

$\vec F=- grad E_p (x,y,z)(10).$

Работа консервативной силы равна изменению потенциальной энергии материальной точки с противоположным знаком, и она не зависит от траектории по которой совершает перемещение частица.

Полная механическая энергия

В общем случае тело обладает и кинетической и потенциальной энергиями одновременно. Сумма данных энергий составляет полную механическую энергию. Полной механической энергией называют физическую величину, равную:

Изменение полной механической энергии материальной точки, которая находится в поле консервативных сил, равно работе, которую выполняют эти силы, оказывающие воздействие на частицу:

Потенциальная и кинетическая энергия способны переходить друг в друга. Полная механическая энергия системы тел, внутри которой действуют исключительно консервативные силы, складывается из потенциальной энергии системы, как единого целого и суммы кинетических энергий, входящих в нее тел.

Источник

Полная энергия

Гамильтониа́н (функция Гамильтона) — функция, зависящая от обобщённых координат, импульсов и, возможно, времени, описывающая динамику механической системы в гамильтоновой формулировке классической механики, а также оператор в квантовой механике и квантовой теории поля. В формализме фейнмановского интеграла по траекториям в квантовой механике и квантовой теории поля используется также и классический гамильтониан (функция Гамильтона).

Гамильтониан (если не зависит от времени) выражает полную энергию системы.

Содержание

Гамильтониан в классической механике

Гамильтониан в квантовой механике

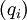
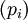
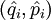
Гамильтониан в квантовой теории — оператор, соответствующий функции Гамильтона в классической теории. Гамильтониан может быть получен заменой обобщённых координат и импульсов в функции Гамильтона классической механики на соответствующие операторы , подчиняющиеся перестановочным соотношениям.

В соответствии с уравнением Шрёдингера гамильтониан определяет эволюцию квантового состояния со временем.

См. также

Ссылки

Полезное

Смотреть что такое «Полная энергия» в других словарях:

полная энергия — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN apparent energy … Справочник технического переводчика

полная энергия W_T — 3.4 полная энергия WT: Суммарная энергия, затраченная на проникновение бойка в испытуемый образец и пробой образца (рисунки 1 3). В отличие от результатов аналогичных испытаний на пробой с измерительной аппаратурой хрупких пластмасс в виде… … Словарь-справочник терминов нормативно-технической документации

полная энергия — visuminė energija statusas T sritis Standartizacija ir metrologija apibrėžtis Visų sistemos energijos rūšių suma. atitikmenys: angl. total energy vok. Gesamtenergie, f rus. полная энергия, f pranc. énergie totale, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas

полная энергия — pilnutinė energija statusas T sritis chemija apibrėžtis Laisvosios ir surištosios energijos suma. atitikmenys: angl. total energy rus. полная энергия … Chemijos terminų aiškinamasis žodynas

полная энергия — pilnutinė energija statusas T sritis fizika atitikmenys: angl. total energy vok. Gesamtenergie, f rus. полная энергия, f pranc. énergie totale, f … Fizikos terminų žodynas

полная энергия ветрового потока — Энергия ветрового потока, проходящего через ометаемую площадь ВК, отнесенная к незаторможенному потоку перед ВК. [ГОСТ Р 51237 98] Тематики ветроэнергетика EN wind energy total … Справочник технического переводчика

полная энергия связи — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN total binding energyTBE … Справочник технического переводчика

полная энергия, распределяемая энергосистемой — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN net electric system energy … Справочник технического переводчика

полная энергия частицы — pilnutinė dalelės energija statusas T sritis radioelektronika atitikmenys: angl. total particle energy vok. Partikelgesamtenergie, f rus. полная энергия частицы, f pranc. énergie totale de particule, f … Radioelektronikos terminų žodynas

удельная полная энергия — Энергия жидкости, равная сумме удельных кинетической энергии, энергии давления и потенциальной энергии … Политехнический терминологический толковый словарь

Источник

Что такое полная энергия системы

Подведем некоторые итоги. В предыдущих параграфах было выяснено, что:

1) если отдельные тела системы движутся с некоторыми скоростями, то от них может быть получена работа за счет уменьшения кинетической энергии этих тел:

где равно сумме изменений кинетической энергии всех тел системы;

2) если в системе тел действуют какие-либо консервативные силы, то работа может быть получена также за счет уменьшения

потенциальной энергии этой стемы:

где

Поэтому можно сказать, что полная работа, которую может отдать такая система, будет всегда равна

Сумма потенциальной и кинетической энергий системы тел получила название полной энергии системы:

Полная энергия системы определяет ту работу, которую можно получить от данной системы тел при ее взаимодействии о какими-либо другими телами, не входящими в эту систему.

Определим сначала, что может происходить с энергией изолированной системы, если телам предоставить возможность свободно двигаться под действием внутренних сил.

Пусть тело массы находится на высоте над поверхностью Земли и имеет скорость (рис. 5.33). В этом положении у тела будет кинетическая энергия и потенциальная энергия Полная энергия системы будет равна

Допустим, что тело перешло на высоту и его скорость стала равной При этом движении сила тяжести совершит работу

Вся эта работа будет израсходована на увеличение кинетической энергии тела:

(Трения и внешних сил нет.) Подставим в это выражение значение работы и перегруппируем члены уравнения:

Левая часть найденного выражения определяет полную энергию системы для начального момента времени:

Правая же часть определяет полную энергию системы для конечного момента времени:

В результате можно записать:

Оказалось, что при движении тел изолированной системы только под действием внутренних сил полная энергия системы не изменяется. При движении тел произошло только превращение части потенциальной энергии в кинетическую. В этом и состоит закон сохранения энергии, который можно сформулировать следующим образом: в изолированной системе тел полная энергия остается постоянной во все время движения тел; в системе происходят лишь превращения энергии из одного вида в другой.

Отсюда же следует, что если на систему действуют какие-либо внешние силы, то изменения полной энергии системы равны работе этих внешних сил.

Если в системе действуют силы трения, то полная энергия системы при движении тел уменьшается. Она расходуется на работу против этих сил. Одновременно работа сил трения производит нагревание. Как уже говорилось ранее, при работе сил трения происходит превращение механического движения в тепловое. Количество выделившегося тепла при этом в точности равно убыли полной механической энергии системы.

Источник

Что такое полная энергия системы

Раздел ОГЭ по физике: 1.18. Механическая энергия. Закон сохранения механической энергии. Формула для закона сохранения механической энергии в отсутствие сил трения. Превращение механической энергии при наличии силы трения.

1. Энергия тела – физическая величина, показывающая работу, которую может совершить рассматриваемое тело (за любое, в том числе неограниченное время наблюдения). Тело, совершающее положительную работу, теряет часть своей энергии. Если же положительная работа совершается над телом, энергия тела увеличивается. Для отрицательной работы – наоборот.

2. Кинетической энергией называется энеpгия движущихся тел. Под движением тела следует понимать не только перемещение в пространстве, но и вращение тела. Кинетическая энергия тем больше, чем больше масса тела и скорость его движения (перемещения в пространстве и/или вращения). Кинетическая энеpгия зависит от тела, по отношению к которому измеряют скорость рассматриваемого тела.

3. Потенциальной энергией называется энергия взаимодействующих тел или частей тела. Различают потенциальную энергию тел, находящихся под действием силы тяжести, силы упругости, архимедовой силы. Любая потенциальная энергия зависит от силы взаимодействия и расстояния между взаимодействующими телами (или частями тела). Потенциальная энергия отсчитывается от условного нулевого уровня.

4. Механической энергией тела называют сумму его кинетической и потенциальной энергий. Поэтому механическая энеpгия любого тела зависит от выбора тела, по отношению к которому измеряют скорость рассматриваемого тела, а также от выбора условных нулевых уровней для всех разновидностей имеющихся у тела потенциальных энергий.

5. Внутренней энергией называется такая энергия тела, за счёт которой может совершаться механическая работа, не вызывая убыли механической энергии этого тела. Внутренняя энеpгия не зависит от механической энергии тела и зависит от строения тела и его состояния.

6. Закон сохранения и превращения энергии гласит, что энеpгия ниоткуда не возникает и никуда не исчезает; она лишь переходит из одного вида в другой или от одного тела к другому.

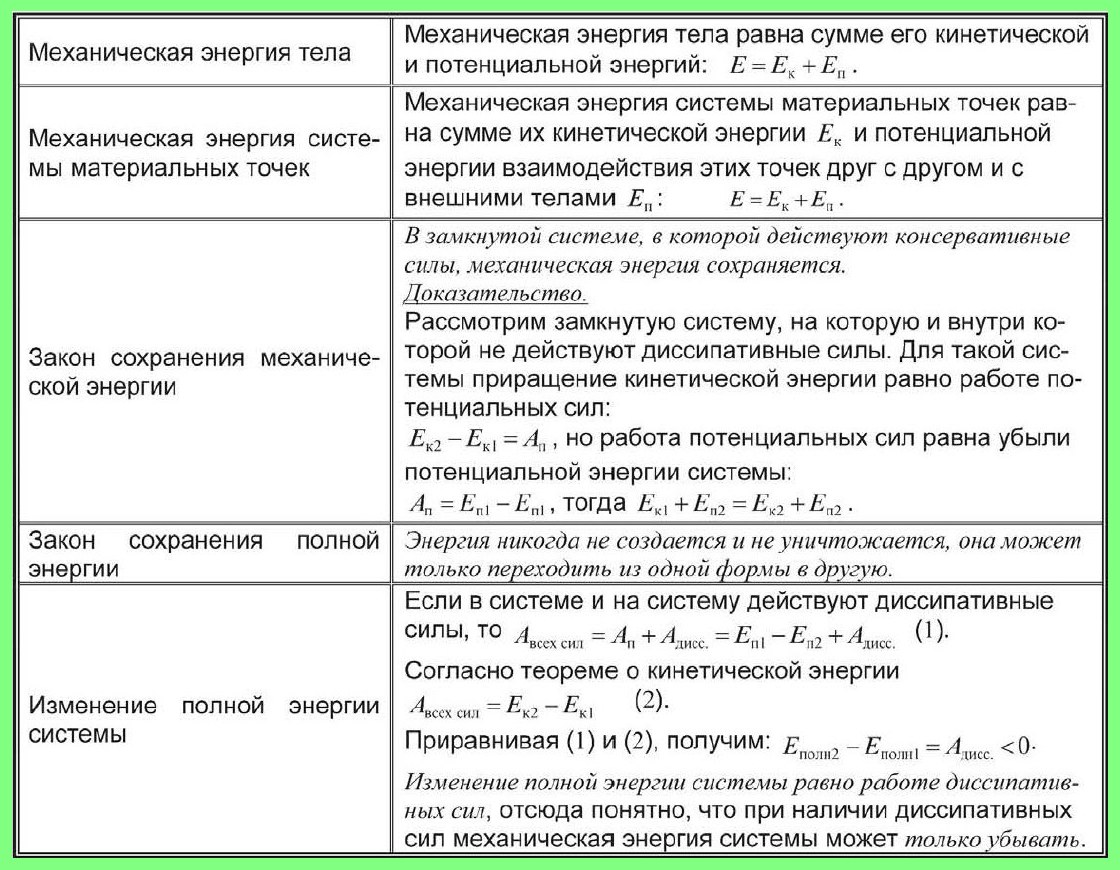
Таблица «Механическая энергия. Закон сохранения энергии».

7. Изменение механической энергии системы тел в общем случае равно сумме работы внешних по отношению к системе тел и работы внутренних сил трения и сопротивления: ΔW = А_внешн + А_диссип

Если система тел замкнута (А_внешн = 0), то ΔW = А_диссип, то есть полная механическая энергия системы тел меняется только за счёт работы внутренних диссипативных сил системы (сил трения).

Если система тел консервативна (то есть отсутствуют силы трения и сопротивления А_тр = 0), то ΔW = А_внешн, то есть полная механическая энергия системы тел меняется только за счёт работы внешних по отношению к системе сил.

Удар, при котором тела до соударения движутся по прямой, проходящей через их центры масс, называется центральным ударом.

Схема «Механическая энергия.
Закон сохранения энергии. Углубленный уровень«

Конспект урока по физике «Механическая энергия. Закон сохранения энергии». Выберите дальнейшие действия:

Источник