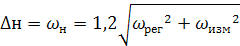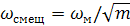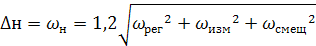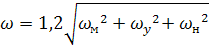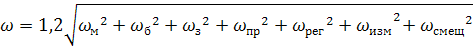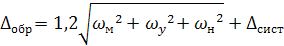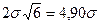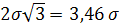что такое поле рассеяния размеров

Что такое поле рассеяния размеров

к случайным погрешностям относятся погрешности, обусловленные изменением величины припуска, колебаниями механических свойств материала, разной силой зажима заготовки при настройке станка, которые для конкретной детали невозможно определить расчетом.

Для оценки точности обработки деталей применяют методы (основанные на математической статистике) построения кривых распределения размеров и точечных диаграмм размеров.

Кривые распределения размеров. Способ построения кривых распределения размеров применим при производстве большого числа одинаковых деталей, обрабатываемых как на предварительно настроенных станках, так и методом пробных рабочих ходов (пробных стружек). Данный способ позволяет оценить точность обработки.

Кривые распределения размеров строят следующим образом. Обрабатывают партии деталей в одинаковых условиях. Затем детали измеряют по одному важному размеру, определяющему точность. При этом оказывается, что, несмотря на одинаковые условия обработки, размеры отличаются друг от друга, хотя в отдельных случаях и совпадают. Разность максимального и минимального размеров, полученных для партии деталей, называют полем рассеивания размеров. Поле рассеивания размеров характеризует точность обработки: чем меньше поле рассеивания, тем точнее принятый метод и условия обработки.

Точность обработки характеризуется также законом распределения размеров (кривая распределения).

Для построения кривых распределения измеряют данный размер на определенном числе деталей n (от 50 до 250). Совокупность измерений деталей разбивают на ряд групп размеров с одинаковыми интервалами. Число групп размеров К определяют по приближенной формуле:

Полученные данные представляют в виде графика, называемого гистограммой распределения, на котором по оси абсцисс откладывают размеры групп, а по оси ординат — число деталей m, размеры которых находятся в пределах соответствующих групп. После нанесения на график точек получают ломаную линию, называемую полигоном распределения. Вместо абсолютного числа деталей m — абсолютной частости в данном интервале размеров — по оси ординат можно откладывать отношение этого числа деталей m к общему числу деталей и в партии; отношение m/n называют относительной частотой, или частостью.

При обработке деталей на металлорежущих станках кривая расселения часто близка к кривой нормального распределения закон Гаусса) (рис. 4.9). При обработке точных деталей (5. 7-й валитет) распределение размеров деталей может следовать другим законам (равной вероятности, треугольника — закон Симпсона и др.)

Кривая нормального распределения выражается уравнением Гаусса

Где х и у текущая абцисса и ордината кривой; хср – среднеарифметическое значение всех размеров; среднеквадратичное всех отклонений.

Среднее значение размера

где хi — значение текущего измерения; n — число произведенных измерений.

Величина хср соответствует максимуму кривой уmах. В этом случае х = xcp

Рис. 4.9. Пример построения кривой нормального распределения (Гаусса):

/ — гистограмма распределения; 2— полигон распределения; 3 — теоретическая кривая нормального распределения

Ветви кривой Гаусса уходят в бесконечность, асимптотически приближаясь к оси X.

Приближенное построение теоретической кривой Гаусса возможно по пяти точкам, координаты которых даны в табл. 4.1.

4.1. Координаты точек для приближенного построения кривой Гаусса

Из уравнения кривой распределения Гаусса следует, что форма кривой определяется величиной среднего квадратичного отклонения а. При уменьшении величины а кривая менее растянута, что соответствует меньшему рассеиванию размеров.

Большим значениям величины а соответствует большее рассеивание размеров — кривая более растянута. На рис. 4.10 приведены кривые нормального распределения при = 1/2, = 1, = 2.

При помощи кривой распределения можно определить вероятное число годных деталей и вероятное число бракованных деталей с размерами, выходящими за поле допуска.

Вследствие действия систематических причин (например, под-наладка станка) кривая распределения может быть двухвершинной (рис. 4.11). В этом случае поле рассеивания увеличивается на величину и допуск на размер (без опасности появления брака) должен быть равен

Определение вероятности возникновения брака при обработке. Брак возникает, если допуск на обработку меньше поля рассеивания размеров. Предположим, что поле 5 установлено двумя размерами х1 и х2 границ этого допуска от среднего размера (рис. 4.12). Вероятное количество годных деталей определяется в этом случае отношением

где F1 и F2 — площади между участками кривых Гаусса и осью абсцисс при размерах x1 и х2; F — площадь между всей кривой Гаусса и осью абсцисс.

При значительном расширении поля допуска (хх =х2 = З.) отношение площадей приближается к единице, так как F1 + F2 = F. В этом случае считают, что вероятность данного достоверного события равна единице.

Определим площади заштрихованных участков F1 и F2 при симметричном распределении кривой распределения относительно оси ординат:

Метод построения кривых распределения размеров сравнительно прост, надежен и поэтому широко применяется для оценки точности размеров деталей при разных методах их обработки. К недостаткам метода следует отнести то, что он в основном дает только суммарную оценку точности обработки и не вскрывает механизм действия разных факторов. Кроме того, метод кривых распределения размеров не учитывает их изменение в процессе обработки при переходе от одной детали к другой, так как вся совокупность деталей рассматривается безотносительно порядка их обработки.

Другие законы распределения. Кроме закона Гаусса существуют и другие законы распределения: закон равной вероятности (рис. 4.13, б), закон треугольника (закон Симпсона. рис. 4.13, г), закон параболы (рис. 4.13, е), сочетание двух законов (Гаусса и равной вероятности), двухвершинная кривая Гаусса и др.

Распределение размеров по закону равной вероятности возникает в том случае, когда увеличение размеров деталей происходит из-за размерного износа инструмента (рис. 4.13, а), т. е. размер деталей х = cn, где с — коэффициент пропорциональности, n — число обработанных деталей.

Если на выполняемый размер влияет закономерно изменяющаяся погрешность вначале замедленно, а затем ускоренно (рис. 4.13, в), то действует закон треугольника (закон Симпсона). Такой закон может быть при совместном действии размерного износа режущего инструмента с сильной фазой начального износа и увеличения силы резания в результате его значительного затупления.

Параболический закон распределения получается в результате тепловых деформаций технологической системы (рис. 4.13, д) от числа обработанных деталей (времени обработки). Кривая распределения размеров приведена на рис. 4.13, е.

Сочетание кривой Гаусса и кривой равной вероятности показано на рис. 4.13, з. Это случай, когда на точность обработки влияет износ инструмента.

Двухвершинная кривая распределения (рис. 4.13, ж, и) получается в случае, если партию деталей обрабатывали при двух различных настройках станка.

Методы точечных диаграмм.

Метод точечных диаграмм размеров. Этот метод дает возможность анализировать точность деталей с учетом последовательности их обработки. Для построения точечной диаграммы по оси абсцисс откладывают номера деталей в последовательности их обработки, а по оси ординат — их размеры, полученные после обработки (рис. 4.14). Для уменьшения длины диаграммы по оси абсцисс вместо номеров деталей откладывают номера групп деталей (например, группа из четырех или пяти деталей), а по оси ординат — размеры всех деталей или средние арифметические значения размеров групп деталей.

Точечные диаграммы позволяют оценить изменение размеров деталей в процессе обработки при переходе от одной детали к другой, т. е. оценить влияние закономерно изменяющихся систематических погрешностей (прежде всего влияние износа режущего инструмента) на точность обработки. В качестве недостатка метода можно отметить, что при наличии нескольких закономерно изменяющихся погрешностей их влияние оценивается суммарно, а не раздельно.

Метод точечных диаграмм используют при применении статистического метода контроля продукции, что ведет к уменьшению числа контролеров и снижению брака. При статистическом методе контроля контролируется не вся партия изготовленных деталей (после обработки всей партии), а выборочно (5. 10% деталей) в процессе обработки на станке. Для регистрации результатов контроля применяют контрольную диаграмму, на которой в увеличенном масштабе нанесены поле допуска и параллельные линии аа и аа, ограничивающие поле допуска примерно по 20 % с каждой стороны. При достижении размера детали (вала), соответствующего контрольной линии аа, подналаживают станок, смещая инструмент в направлении детали. Обычно настроечный размер при точении по наружному диаметру бывает в нижней части допуска, чтобы увеличить продолжительность работы без подналадки станка из-за износа резца. Таких подналадок может быть одна-две, после чего меняют затупленный резец на острый.

Источник

Рассеяние размеров, связанное с погрешностью настройки

Погрешность настройки станка D_н = w_н изменяется как случайная величина в результате воздействия погрешности регулирования w_рег положения режущего инструмента и отдельных узлов станка относительно установленного инструмента и под влиянием погрешности измерения w_изм пробных заготовок, по которым производится настройка станка.

Погрешность положения режущего инструмента на станке определяется точностью используемых при настройке регулировочных средств (лимбов, индикаторов, миниметров, упоров и др.). При упрощенных расчетах точности обработки w_рег можно принимать равной цене деления регулировочного устройства или предельной погрешности мерительного инструмента, с помощью которого регулируют положение режущего инструмента. Точность установки требуемого положения отдельных узлов станка (например, стола фрезерного станка по высоте относительно положения шпинделя) относительно установленного режущего инструмента зависит от конструкции и состояния станка и определяется по его характеристикам.

Погрешность измерения w_изм пробных заготовок принимается равной предельной погрешности используемого измерительного инструмента.

Суммарная погрешность настройки в общем случае определяется выражением

При настройке станков по пробным заготовкам с помощью универсального измерительного инструмента на погрешность настройки оказывает дополнительное влияние величина смещения w_смещ центра группирования групповых средних, которая определяется формулой

Общее (суммарное) рассеяние размеров заготовок и общая погрешность обработки. Суммарное поле общего рассеяния размеров партии заготовок, обработанных на настроенном станке по методу автоматического получения размеров, выражается формулой

или в развернутом виде

Общая погрешность обработки D_обр включает в себя все поля рассеяния размеров заготовок под влиянием причин случайного характера, а также систематические и переменные систематические погрешности обработки, т. е.

Величина D_сист представляет собой алгебраическую сумму неустранимых при настройке станка систематических погрешностей, возникающих при обработке заготовок и влияющих на их размеры, и наибольших значений переменных систематических погрешностей.

Ранее было отмечено, что систематические погрешности не изменяют форму кривой рассеяния размеров обрабатываемых заготовок, а только сдвигают положение ее вершины, соответственно увеличивая общее поле колебания размеров партии обработанных заготовок, а следовательно, и общую погрешность обработки. Особенно большое практическое значение при этом имеет определение величин и знаков переменных систематических погрешностей.

Известно, что переменные систематические погрешности, обусловленные износом режущего инструмента, изменяются по закону равной вероятности. Однако при нахождении суммарной погрешности обработки заготовок определять полную долю погрешности, вызываемую износом режущего инструмента, по этому закону практически не всегда нужно, так как эта составляющая погрешности задается при настройке станков, исходя из условий проведения операции и необходимого периода работы станка между его поднастройками, которые компенсируют смещение центра группирования размеров, связанное с износом инструмента.

Погрешности, вызываемые тепловыми деформациями технологической системы (смещение передней бабки токарного или шлифовального станка в направлении на рабочего, удлинение резцов и др.), обычно имеют знак, противоположный погрешностям, обусловленным износом инструмента, и в период тепловых деформаций (период разогревания технологической системы до наступления ее тепловой стабилизации, устанавливающейся через несколько часов после начала работы станка) могут уменьшать влияние износа инструмента.

Для уменьшения погрешности настройки D_н = w_н необходимо сократить погрешность измерения w_изм пробных заготовок путем применения более точного измерительного инструмента и погрешность регулирования w_рег за счет использования более точных установочных устройств.

Снижения погрешности закрепления w_з можно достигнуть в результате применения более совершенных конструкций приспособлений, предусматривающих плотный прижим базирующих поверхностей заготовок к жестким и точным установочным элементам, а также за счет использования при построении операции настроечных или проверочных технологических баз.

Погрешность базирования D_б = w_б можно устранить полностью или свести до минимума посредством правильного выбора формы установочных элементов приспособлений, базирующих поверхностей заготовок и правильной простановки размеров в чертеже заготовки, предусматривающей совмещение технологических и измерительных баз.

Только после использования всех указанных способов уменьшения погрешностей обработки следует анализировать возможности сокращения мгновенного рассеяния w_м. Это связано с тем, что для снижения w_м обычно приходится заменять производительные и экономичные способы обработки на автоматах и револьверных станках обработкой на более точных, но менее производительных токарных, шлифовальных и доводочных станках.

Изложенная методика расчета рассеяния размеров заготовок и общей погрешности их обработки на станках рекомендуется для использования в проектно-технологических организациях и в отделах Главного технолога завода при выполнении проектных расчетов для сопоставления точности обработки заготовок при разных вариантах технологических процессов на различных станках и с разной технологической оснасткой. В этом случае в расчет следует вводить данные о значениях отдельных составляющих погрешностей и рассеяния, приведенные в литературе, справочниках и заводских нормативах.

ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ РАЗМЕРОВ ДЛЯ АНАЛИЗА ТОЧНОСТИ ОБРАБОТКИ

Изложенные законы распределения размеров используются в технологии машиностроения для установления надежности проектируемого технологического процесса в обеспечении обработки заготовок без брака; расчета количества вероятного брака при обработке; определения количества обработанных заготовок, требующих дополнительной обработки; расчета экономической целесообразности использования высокопроизводительных станков пониженной точности; расчета настройки станков; сопоставления точности обработки заготовок при различном состоянии оборудования, инструмента, смазочно-охлаждающей жидкости и т. п.

Установление надежности обработки заготовок без брака. Надежность обеспечения требуемой точности обработки заготовок характеризуется запасом точности y данной операции, который определяется по формуле

Величина поля рассеяния w при различных законах распределения размеров обрабатываемых заготовок приводится ниже.

Нормальное распределение (закон Гаусса) 6s

Равнобедренный треугольник (закон Симпсона)

Равная вероятность

Эксцентрисет (закон Релея) 3,44s_o; 5,25s_r

Линейная функция a(t)

Когда запас точности y > 1,0, обработка заготовок может быть осуществлена без брака (при условии правильной настройки станка, обеспечивающей совмещение вершины кривой рассеяния с серединой поля допуска). При y 1,2 процесс обработки считается надежным. Для всех законов распределения размеров условием обработки заготовок без брака является выражение w

Источник

Большая Энциклопедия Нефти и Газа

Поле рассеивания размеров заготовок после каждой операции разбивается на равное число интервалов. Каждому интервалу присваивается номер. [2]

Иногда поле рассеивания размеров было в 2, 5, 6, 12, 15 раз больше поля допуска для данного размера ( см. рис. 3 и 4); причем эти цифры относятся к таким важнейшим параметрам, как задний угол сверла, утолщение сердцевины, осевое биение режущих кромок, обратный конус сверла, падение затылка метчика, половина угла профиля резьбы метчика, отклонение шага резьбы и др. Это свидетельствует о большой дисперсии размеров, контролируемых параметров сверл и метчиков. [4]

Разделим поле рассеивания размеров на три зоны. [5]

Разбиваем поле рассеивания размеров на равное число интервалов. [6]

Определяют поле рассеивания размеров деталей как приближенную меру их точности. Поле рассеивания размеров определяется на основе рассчитываемых параметров соответствующего теоретического закона распределения. [7]

Величина поля рассеивания размеров зависит от величины суммарной погрешности обработки, поэтому с технологических позиций точность обработки следует определять величиной Суммарной погрешности обработки, возможной при изготовлении совокупности настроечных партий деталей. [9]

При симметричном расположении поля рассеивания размеров относительно поля допуска ( см. фиг. [11]

Размерный брак возникает, когда поле рассеивания размеров обработанных на станке деталей не укладывается в пределы поля допуска. [15]

Источник

Рассеивание размеров обрабатываемых заготовок и законы распределения размеров

Размеры двух любых деталей, взятых из одной партии, различны. У деталей одной партии, изготовленных в одинаковых условиях, можно установить максимальное значение разности их размеров, или поле рассеивания размеров. Он охарактеризует точность вы бранного метода обработки для данных производственных условий.

Неточность обработки поверхностей является результатом влияния различных факторов, которые вызывают погрешности. Теорией и практиком технологии машиностроения установлено, что действие

этих факторов характеризуется полем рассеивания размеров и законом распределения размеров (кривая распределения и характеризующие ее параметры). На основании этого закона при решении практических задач, касающихся точности обрабатываемых заготовок, применяют методы, рекомендуемые математической статистикой и теорией вероятности. Пользуясь этими методами, можно расчетно-аналитическим путем определить наиболее вероятные значения размеров обрабатываемой заготовки при данных условиях обработки.

В зависимости от степени влияния различных факторов, действующих в процессе получения размеров, можно получить весьма разнообразные формы кривых, характеризующих законы распреде ления. Наиболее характерными являются: кривая распределения по закону равной вероятности, кривая распределения по закону Симпсона и кривая распределения по закону Гаусса, или, как часто его называют, закону нормального распределения.

Источник

2.4.2. Составляющие общего рассеяния размеров деталей

Рассеяние размеров изготавливаемых деталей вызывается многочисленными случайными факторами различного характера, оказывающими своё воздействие на отдельные элементы технологической системы одновременно и независимо друг от друга. По своему происхождению эти факторы могут быть объединены в определённые группы, вызывающие свою долю общего рассеяния размеров.

Рассеяние размеров, связанное с видом обработки (мгновенное рассеяние). Каждому виду обработки, осуществляемому на определённом оборудовании, свойственна своя величина рассеяния размеров,

характеризуемая полем ω м рассеяния. Однако и внутри данного вида обработки

значение ω м изменяется в зависимости от конструкции, типоразмера и состояния станка (т.е. от его точности и жёсткости). Развитие конструкции станков и появление их новых типоразмеров могут вызывать переоценку установившихся представлений о рассеянии размеров при данном виде обработки. Рассеяние размеров, связанное с видом обработки, не остаётся постоянным и в продолжении обработки партии заготовок, а изменяется в зависимости от состояния режущего инструмента (рис. 2.7, а). В начале (начальный износ инструмента) и в конце (интенсивный катастрофический износ и разрушение инструмента) обработки партии заготовок поле рассеяния ω м нач и ω м конеч больше, чем ω м ср в середине обработки партии (рис. 2.10, б).

Рис. 2.10. Износ режущего инструмента (а) и изменение поля мгновенного рассеяния размеров изнашиваемой детали (б)

Рассеяние размеров в каждый данный момент времени (мгновенное рассеяние) определяется факторами, не зависящими от нагрузки (зазором в подшипнике шпинделя, неравномерностью процесса резания) и оказывающими влияние на нагрузку (колебаниями припусков на обработку, колебаниями твёрдости обрабатываемого материала).

Рассеяние размеров, связанное с погрешностью установки. При установке заготовки на станке для обработки методом автоматического получения размеров достигаемая точность размеров зависит от положения измерительной базы заготовки относительно режущего инструмента. Колебание положения измерительной базы заготовки является причиной возникновения погрешности

базирования) можно определить как разность предельных расстояний измерительной базы заготовки относительно установленного на размер инструмента. Поле рассеяния размера а (рис. 2.8, а), связанное с погрешностью

Источник