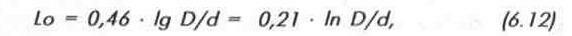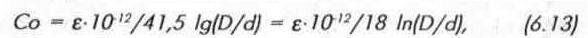что такое погонная индуктивность

6.1. Разновидности линий.

6.1. Разновидности линий.

Существует несколько видов линий передачи высокочастотной энергии. Для выполнения междуэтажных или междурядных соединений в сложных синфазных антеннах применяются двухпроводные воздушные линии (рис. 6.1.).

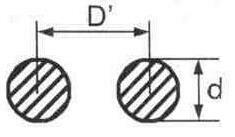
Рис. 6.1. Поперечное сечение двухпроводной неэкранированной линии из проводов круглого сечения

Интервал величины волнового сопротивления этих линий может быть достаточно широким. Оба провода воздушной симметричной линии должны располагаться строго симметрично относительно друг друга и земли, что является ее недостатком, так как практически трудно выдержать одинаковые расстояния между проводами на протяжении всей длины линии, а также между каждым проводом и землей. Волновое сопротивление для линии из проводов круглого сечения зависит от отношения расстояния между двумя проводниками к их диаметру, и определяется по формуле

Формула справедлива при Ь>3а и d Z (6.7)

где Z — волновое сопротивление линии;

R — сопротивление нагрузки линии.

Следовательно, этот коэффициент характеризует собой степень согласования линии с нагрузкой. При R=Z oн равен единице, что означает полное согласование линии с нагрузкой, при котором в линии будет режим бегущей волны.

В действительности такие линии не существуют из-за невозможности идеального согласования нагрузки с линией.

Величина, обратная коэффициенту бегущей волны, называется КОЭФФИЦИЕНТОМ СТОЯЧЕЙ ВОЛНЫ:

Отношение амплитуд напряжения отраженной и падающей волн

называется КОЭФФИЦИЕНТОМ ОТРАЖЕНИЯ, который определяется из формул:

Измеряют амплитуды напряжений падающей и отраженной волн с помощью направленных ответвителей.

6.1.2. Параметры фидерных линий

Основными параметрами линии передачи являются волновое сопротивление, погонная емкость, погонное затухание.

ВОЛНОВЫМ СОПРОТИВЛЕНИЕМ ЛИНИИ (Z) называется отношение комплексных амплитуд напряжения к току падающих или отраженных волн. Оно носит комплексный характер и связано с погонной индуктивностью Lo и погонной емкостью линии Со соотношением:

Для коаксиальных кабелей Lo и Со определяются по формулам:

где D — диаметр [внутренний) экрана, мм;

d— диаметр внутреннего проводника, мм.

Погонная емкость кабеля — емкость единицы длины кабеля. Обычно погонная емкость кабеля указывается в пф/м:

где е — диэлектрическая проницаемость изоляции;

D — диаметр (внутренний) экрана, мм;

d—диаметр внутреннего проводника, мм.

Значения диэлектрической проницаемости e материалов приведены в приложении 9.

Волновое сопротивление коаксиального кабеля определяется геометрическими размерами его поперечного сечения и диэлектрической постоянной [см. формулу 6.4).

Электромагнитная волна в фидерной линии с диэлектриком распространяется с меньшей скоростью, чем в свободном пространстве (для вакуума, е = 8,854*10^(-12)). Так, в воздушной линии скорость распространения волны всего на 2-3% меньше, чем в свободном пространстве, а в кабельной линии, заполненной диэлектриком, скорость зависит от диэлектрической проницаемости материала заполнения,

В зарубежной справочной литературе вместо коэффициента укорочения длины волны приводят КОЭФФИЦИЕНТ ЗАМЕДЛЕНИЯ ЛИНИИ ПЕРЕДАЧ, (k = 1/с). Радиоволны в свободном пространстве распространяются со скоростью света ( с = 3*10^8 м/с). В линии передачи их скорость уменьшается в k раз. Значения k меняются в зависимости от конструкции линии.

0,75 — для двухпроводной линии с пластмассовой изоляцией;

0,67 — для коаксиальной линии с твердой пластмассовой изоляцией;

0,85 — для коаксиальной линии с воздушной изоляцией;

0,97 — для открытой воздушной двухпроводной линии. Вследствие потерь электромагнитная волна, распространяясь вдоль линии, уменьшается по величине — затухает. Эффективность прохождения сигнала по линии (фидеру) определяется величиной погонного затухания (Р). ПОГОННОЕ ЗАТУХАНИЕ характеризуется уменьшением напряжения сигнала по мере его распространения вдоль линии на рабочей частоте, приходящееся на единицу длины кабеля. Выражают затухание в децибелах на метр (или неперах на километр).

При небходимости перевода единиц затухания можно воспользоваться следующим соотношением: 1дБ = 0,115 неп (или 1неп = 8,686дВ).

Погонное затухание зависит от материалов, из которых изготовлены проводники и изоляция, их поперечных размеров, частоты измерения и определяется по формуле

Чем выше частота и чем длиннее кабель, тем больше затухание Р фидерной линии.

ПРИМЕР: Определить общее затухание фидерной пинии, выполненной из коаксиального кабеля РК-75-4-11 длиной l=25м для V-TB канала. Из табл. 1.2 находим частоту V-TB канала: Fср=96МГц. По табл. 6.3 определяем затухание кабеля на этой частоте в=0.1 дБ/м. Общее затухание составит T=в*l;T=0.1*25=2.5дБ

Уменьшение напряжения сигнала, по мере его распространения вдоль линии, происходит по экспоненциальному закону:

Затухание сигнала по мощности в фидерной линии определяется формулой

КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ линии определяется как отношение мощности на выходе линии к мощности на ее входе:

Из формулы следует, что чем меньше коэффициент погонного затухания линии и меньше ее длина, тем больше КПД.

Источник

Расчёт межпроводной индуктивности и ёмкости симметричных прямых пар методами Конформных отображений и конечных элементов

Этой работой мы открываем цикл статьей, посвящённых расчёту погонных ёмкостей и индуктивностей – важнейших первичных параметров любых кабельных конструкций: для передачи информации (телефонные и телеграфные провода, витые пары, коаксиальные кабели. ), для передачи энергии (силовые кабели, воздушные линии электропередач. ) и специального назначения (триады, каротажные кабели, подводные, шахтные, нефтяные. ). Потому что именно ёмкость и индуктивность определяют скорость сигналов и волновое сопротивление линий. И, следовательно, величину и распространение напряжений и токов. А также искроопасность кабелей, используемых во взрывоопасных зонах.

Не исключено, что такое намерение может кого-то удивить, так как существует огромное количество учебной и методической литературы, а также фундаментальных монографий, посвящённых данному предмету. Как основополагающих трудов старых и заслуженных мастеров [1,2], так и современных [3,4]. И что здесь можно сказать существенно новое?

Тем не менее, неумолимый ход Времени заставляет по-новому взглянуть и на эту отрасль расчётной деятельности. Которая, казалось бы, досконально изучена и отшлифована десятилетиями труда многих и многих поколений инженеров.

21-й век начался как век информационных технологий и энергетики. Но прогресс этих отраслей невозможен без адекватного, а лучше и опережающего, развития кабельной индустрии – производства средств передачи сигналов и энергии. Этот процесс сопровождается быстрым ростом номенклатуры кабельных изделий и их компонентов, галопом цен на проводниковые и изолирующие материалы и общим ужесточением требований к качеству.

Всё вместе обусловливает ужесточение требований к точности технологических режимов и регламентов, к точности и достоверности контроля качества исходных материалов и продукции. А также значительное увеличение затрат на разработку новых изделий. Последнее не в малой степени обусловлено низкой точностью и достоверностью применяемых до сих пор методик расчёта.

Это связано с тем, что указанные методики основаны на применении формул, полученных более полувека назад для некоторых простейших геометрий проводников и изоляторов. И в практическом применении они – всего лишь приближения. Не спасают и поправочные коэффициенты для геометрий, более приближенных к реальным, но тоже достаточно простым. Так как на все случаи жизни поправок нет, и результаты таких «расчётов» (а точнее говоря, оценок) зависят от произвола или, говоря мягче, интуиции расчётчика.

Конечно, интуиция мастера, за плечами которого не один десяток лет и тысячи километров кабелей – вещь ценная. Но в условиях быстрых изменений она может и подводить. Помимо прочего, её вообще надо освободить от тупой расчётной рутины. Это тем более необходимо, что существенный прогресс в расчётном деле давно отсутствует. Чтобы убедиться в этом, достаточно сравнить упомянутые выше работы, разделённые полувеком.

Они же вооружили нас мощными персональными компьютерами. И тем самым закрыли эпоху арифмометров и номограмм, приближённых формул и поправок к ним. Открыв дорогу новым, «абсолютным» расчётным технологиям. Которые, как представляется, должны:
1.Обеспечить расчёт проектируемого изделия из «первых принципов».
2.Исключить какие-либо приближения и поправки.
3.Обеспечить расчёт с любой, наперёд заданной, степенью точности.

Здесь, однако, требуется уточнение. Дело в том, что устройство даже простейших кабельных сборок на самом деле настолько сложно, что оно не зубам даже самым продвинутым суперкомпьютерам. И для расчётов требуются упрощения, то есть работа интуиции. А вот как раз после этого расчёт и должен отвечать указанным выше требованиям.

Существуют разные методы расчёта электрических параметров «из первых принципов»:
— с помощью вариационных процедур;
— методом конечных разностей;
— методом конечных элементов.

∫E 2 dω (интеграл по всему объёму ω поля).

Во втором дифференциальное уравнение заменяют системой алгебраических для конечных разностей. Где, например, производную ∂U/∂x заменяют частным ΔU/Δx.

Третий способ – как бы гибрид первых двух. Здесь объём ω покрывают сеткой небольших участков – конечных элементов, обычно в форме симплексов (на плоскости – это треугольники, в трёхмерном объёме – тетраэдры). Внутри элементов поле представляют приближением, зависящим от подгоночных параметров. Например, для двумерных задач – плоскостями, проходящими через 3 узла сетки. И подбирают параметры с таким расчётом, чтобы значения U(x,y) в узлах сетки обеспечивали минимум энергии поля, а на границах – граничные условия. Более подробно с этим методом можно ознакомиться в [5].

Разработано множество программ для решения задач с конечными элементами: ANSYS, NASTRAN, PATRAN. Но для них необходимо мощное оборудование и высокая квалификация расчётчиков. Для решения двумерных задач (а к таковым относится большинство кабельных) более пригоден пакет ELCUT [6].

Поэтому предлагаемый вниманию цикл работ мы посвящаем исследованию существующей и доступной версии ELCUT, имея в виду его перспективы в реализации указанной выше «абсолютной» расчётно-кабельной технологии.

Забегая вперёд, отметим, что, как представляется на настоящий момент, в полном объёме это реализуемо лишь для «прямых» кабельных систем, то есть таких, где можно пренебречь эффектами скрутки. Кроме того, при известном искусстве, можно получить оценки влияния скрутки на ряд параметров линий. Есть, однако, и такие «скрученные» параметры, которые в существующей версии ELCUT оценить нельзя. Хотя сам по себе его метод позволяет точно решать все эти задачи. Так что у ELCUT есть перспектива стать основным расчётным инструментом в кабельно-расчётном деле. Но, после надлежащей доработки, о чем подробнее в последующих статьях.

Если, однако, отвлечься от таких деталей, то уже первое знакомство с ELCUT убеждает в полезности этого инструмента в инженерной деятельности. Но у него есть два недостатка:
— конечный размер геометрических моделей;
— решение двумерных задач.

Первый ограничивает ELCUT при расчёте первичных параметров – погонной ёмкости и индуктивности линий с распределёнными параметрами.

Дело в том, что часть кабельной продукции оборудуют металлическими экранами, естественным образом ограждающими область электромагнитного поля в ELCUT. Но вот основная масса: телефонные линии, бытовая электропроводка, витые пары низших категорий, линии электропередач экранами не оборудованы. И в ELCUT такие задачи решают приближённо (пример – разбираемая ниже задача Lab3_Сu, приведенная в доступной для широкой общественности библиотеке демонстрационных программ).

Второе ограничивает тем, что многие практически важные кабельные объекты – структуры трёхмерные, так как при сборке сердечников кабелей их токопроводящие жилы, как правило, скручивают между собой. Равно как и сами жилы, если их свивают из нескольких (7, 19 и т.д.) проволок. И потому, на первый взгляд, применение ELCUT тут невозможно.

Тем не менее, обе эти задачи здесь могут быть решены: как точный расчёт неэкранированных кабельных конструкций, так и оценка влияния всех видов скруток.

Цель настоящей работы – показать, как без потерь точности решить (любую) «неэкранированную» задачу. А скрутки оставим для обсуждения в последующих статьях.

Индуктивность неэкранированной пары в решении задачи Lab3_Сu (http://www.tor.ru/elcut/courses/ toe/rus/lab3_r.htm).

Сначала разберём решение этой задачи, посвящённой моделированию магнитного поля бесконечной прямой симметричной двухпроводной медной линии (рис.1) по которой течёт переменный ток J = 300A. Изолятор – воздух (в отличие от рассматриваемой ниже пары с изолированными проводами). Провода толстые и близкие: a =15 мм и b = 59 мм, так что существенны скин-эффект и эффект близости.

Здесь есть две плоскости зеркальной симметрии: одна проходит через оси проводников, рассекая их, а вторая, перпендикулярная ей, – через середину расстояния между проводами. Поэтому геометрическую модель задаче строят лишь в одном квадранте. В целом линия открыта в Космос и вектор-потенциал её магнитного поля А

1/Д (Д – расстояние от линии).

По этой причине в Lab3_Сu квадрант ограничили квадратом со стороной Д =1000 мм >> a, b. На стороне квадрата, рассекающей проводники, касательная составляющая магнитного поля Нt = 0.На остальных трёх сторонах А = 0. Отметим, что на плоскости симметрии А = 0 точно, а на остальных сторонах – лишь приближённо.

С = εε₀π / ln[b/a + (b 2 /a 2 –1) 1/2 ] ;

L = μ₀/π ln[b/a + (b 2 /a 2 – 1) 1/2 ] = 0.81843 МкГн/м (3)

Межпроводная индуктивность конформно преобразованной пары.

Тогда решаемое в ELCUT уравнение Пуассона:

преобразуется к виду :

R 4 [ ∂ (R ∂ A/ ∂ R)/ ∂ R/R + ∂ 2 A/ ∂ φ 2 /R 2 ] /M 2 + i µ₀ g ω A = – µ₀ j_стор (5)

где: R = [u 2 + v 2 ] 1/2 = М 2 /r

В ELCUT величину j_вихр = i µ₀ g ω A называют плотностью вихревых токов, j_стор – плотностью сторонних токов. По физическому смыслу первый – это ток самоиндукции проводника, вызываемый переменным магнитным полем протекающего через него тока j = j_вихр + j_стор, а второй по величине равен постоянному току, который протекал бы через проводник при том же падении напряжения на нём (то есть при отсутствии индуктивного сопротивления).

∂ (r ∂ A/ ∂ r)/ ∂ r + ∂ 2 A/ ∂ φ 2 /r 2 = 0 ;

∂ (R ∂ A/ ∂ R)/ ∂ R + ∂ 2 A/ ∂ φ 2 /R 2 = 0

То есть, в изоляторах конформное преобразование не меняет вид уравнения Лапласа (отметим попутно, что дробно-линейное отображение в некотором смысле не меняет и вид уравнений Пуассона (4) и (5) [9] ). Это значит, что вместо приближённого решения безграничной задачи можно точно решить ей конформную, ограниченную экраном, в который отображаем один из проводов. В данном случае – получить точно известные индуктивность и ёмкость коаксиального кабеля:

Проверим это с помощью ELCUT, для чего вычислим поток Ф магнитного поля вокруг жилы с током. Для этого достаточно вычислить поле в узком секторе (100 на рис. 4).

Тогда получим L = Ф / J = 0.81878 мкГн/м, что всего на 0.04% больше точного. И это всего при 254 узлах сетки (0.14%, если узлов 119). Отметим попутно, что в ELCUT предусмотрен ещё более точный и быстрый способ вычисления индуктивных параметров, о чём подробнее – в одной из следующих статей.

Отображение пар в структуры, близкие к коаксиальным, полезно ещё и потому, что такие структуры имеют широкий минимум ёмкости (максимум индуктивности). На рис.5 представлены графики зависимости ёмкости от смещения жилы относительно центра экрана. Как видно, небольшое смещение осей экрана и/или провода мало влияет на ёмкость. Цифры около кривых – отношение а’2/a’1.

Отметим, что такое смещение можно рассматривать и как частный случай искажения формы провода и/или экрана. Поэтому можно ожидать, что если пару произвольных проводов отобразить в почти коаксиальную фигуру, то выражения (3’) дадут неплохое приближение к параметрам пары, точность которого можно оценить с помощью кривых на рис.5. Кроме того, практическая полезность данного наблюдения ещё и в том, что, получая точные значения параметров кабеля в среде ELCUT, расчётчик легко сравнит их с традиционными оценками, которые производят до сих пор с помощью (3’).

Емкость неэкранированной прямой симметричной пары.

Тогда пара отобразится в коаксиальную структуру с радиусом жилы a₁ = a = 1.000 мм, экрана a₂ = a [b/a ± (b 2 /a 2 – 1) 1/2 ] 2 = 4.540 мм и центром 2.131 мм. (рис.6). Границы изоляции отобразятся в две касающиеся эксцентричные окружности с радиусами a₄ = 3.131 мм (центр 1.1304 мм ) и a₃ = 1.615 мм (центр 2.647 мм ).

На основании этих данных строим геометрическую модель ELCUT и вычисляем ёмкость пары C = 61.13 пФ/м с погрешностью не больше 0.1% при числе узлов

Картина поля вокруг пары – это (обратное) конформное отображение линий потенциала, изображённых на рис. 6. Если необходимо, можно пересчитать и отобразить другие величины и объекты. Но здесь в этом нет надобности.

Выводы

1. С помощью ELCUT можно точно вычислить параметры любой открытой системы проводников, если с помощью конформного преобразования, например, дробнолинейного, отобразить её закрытую экраном. Поэтому дополнение математического инструментария ELCUT мастером (прямых и обратных) конформных отображений хотя бы в объёме справочника [10] позволит обеспечить максимальную точность вычислений межпроводной ёмкости и индуктивности любых нескрученных кабельных конструкций.

2. В общем случае конформное отображение модифицирует вид уравнений Лапласа и Пуассона. Например, появляются коэффициенты, пропорциональные степеням радиуса R. Потому целесообразно научить ELCUT работать с произвольными координатно-зависимыми коэффициентами при производных, а также координатно-зависимыми плотностями зарядов и токов в блоках (в правых частях уравнения (4), о чём подробнее в следующей статье).

Тогда ELCUT имеет шанс стать весьма востребованным инструментом в кабельно-расчётном деле.

Подробнее о конформном отображении можно прочитать в монографии:

К.Каратеодори Конформное отображение. – М.-Л.: ОНТИ Государственное технико-теоретическое издательство, 1934. Книгу можно скачать из библиотеки мехмата МГУ http://lib.mexmat.ru/books/1663

Достаточно подробное изложение можно найти в статьях пятитомника «Математическая Энциклопедии». – М: БСЭ, 1979.

Нашли ошибку? Выделите и нажмите Ctrl + Enter

Источник

Длинная линия

Длинная линия

Содержание

1 Дифференциальные уравнения длинной линии
1.1 Погонные параметры 1.2 Эквивалентная схема участка длинной линии 1.3 Телеграфные уравнения 1.4 Условие регулярности линии 1.5 Однородные волновые уравнения длинной линии 1.6 Распределение поля падающей волны

2 Комплексный коэффициент отражения по напряжению 3 Коэффициенты бегущей и стоячей волны 4 Входное сопротивление длинной линии 5 Режимы работы длинной линии

5.1 Режим бегущей волны 5.2 Режим стоячей волны 5.3 Режим смешанных волн

6 Линия без потерь

6.1 Разомкнутая линия 6.2 Замкнутая линия 6.3 Ёмкостная нагрузка 6.4 Индуктивная нагрузка 6.5 Активная нагрузка 6.6 Комплексная нагрузка

7 КПД линии с потерями 8 Пределы применимости теории длинной линии 9 См. также 10 Примечания

Длинная линия — регулярная линия передачи[1], длина которой превышает длину волны (λ) колебаний, распространяющихся в линии.

Характерной особенностью длинных линий является проявление интерференции двух волн, распространяющихся навстречу друг другу. Одна из этих волн создается генератором электромагнитных колебаний, подключенным к линии, и называется падающей. Другая волна может возникать из-за отражения падающей волны от нагрузки, подключенной к противоположному концу линии, и называется отраженной. Отраженная волна распространяется в направлении, обратном падающей волне. Все разнообразие процессов, происходящих в длинной линии, определяется амплитудно-фазовыми соотношениями между падающей и отраженной волнами.

Дифференциальные уравнения длинной линии

Рассмотрим двухпроводную длинную линию, представленную на рисунке 1. На рисунке обозначено: ZН = RН + iXН — комплексное сопротивление нагрузки; z — продольная координата линии, отсчитываемая от места подключения нагрузки.

Погонные параметры

Рис.1 — К выводу дифференциальных уравнений длинной линии

Из электродинамики известно, что линия передачи может быть охарактеризована ее погонными параметрами:

R1 — погонное сопротивление, Ом/м; G1 — погонная проводимость, 1/Ом м; L1 — погонная индуктивность Гн/м; C1 — погонная ёмкость Ф/м;

Погонные сопротивление R1 и проводимость G1 зависят от проводимости материала проводов и качества диэлектрика, окружающего эти провода, соответственно. Чем меньше тепловые потери в металле проводов[2] и в диэлектрике, тем меньше соответственно, R1[3] и G1[4]. Погонные индуктивность L1 и емкость C1 определяются формой и размерами поперечного сечения проводов, а также расстоянием между ними.

Эквивалентная схема участка длинной линии

Рис.2 — Эквивалентная схема участка длинной линии

Выделим из линии элементарный участок бесконечно малой длины dz и рассмотрим его эквивалентную схему, покзанную на рисунке 2. На этой схеме стрелками обозначены направления отсчета напряжения U и тока I в линии; dU и dI — приращения напряжения и тока в линии на элементе длины dz. Значения параметров схемы определяются соотношениями:

Используя эквивалентную схему, запишем выражения для приращений напряжения и тока:

Подставляя сюда значения параметров схемы из (1), получаем:

,

где Z1 = R1 + iωL1, Y1 = G1 + iωC1 — погонные комплексные сопротивление и проводимость линии. Из последних соотношений находим дифференциальные уравнения линии:

Телеграфные уравнения

Основная статья: Телеграфное уравнение

Эти соотношения называются телеграфными уравнениями длинной линии. Они определяют связь между током и напряжением в любом сечении линии. Решим телеграфные уравнения относительно напряжения и тока. Для этого продифференцируем их по z:

При этом учтем, что:

Условие регулярности линии

Данные соотношения являются математическим определением регулярности длинной линии. Смысл соотношения (4) состоит в неизменности вдоль линии ее погонных параметров.

Подставляя в (3) значения производных напряжения и тока из (2), после преобразований получаем:

Однородные волновые уравнения длинной линии

,

где γ — коэффициент распространения волны в линии: .

Соотношения (5) называются однородными волновыми уравнениями длинной линии. Их решения известны и могут быть записаны в виде:

,

где AU, BU и AI, BI — коэффициенты, имеющие единицы измерения напряжения и тока соответственно, смысл которых будет ясен ниже.

Решения волновых уравнений в виде (3.6) имеют весьма характерный вид: первое слагаемое в этих решениях представляет собой падающую волну напряжения или тока, распространяющуюся от генератора к нагрузке, второе слагаемое — отраженную волну, распространяющуюся от нагрузки к генератору. Таким образом, коэффициенты AU, AI представляют собой комплексные амплитуды падающих волн напряжения и тока соответственно, а коэффициенты BU, BI — комплексные амплитуды отраженных волн напряжения и тока соответственно. Так как часть мощности, передаваемой по линии, может поглощаться в нагрузке, то амплитуды отраженных волн не должны превышать амплитуды падающих:

Направление распространения волн в (6) определяется знаком в показателях степени экспонент: плюс — волна распространяется в отрицательном направлении оси z; минус — в положительном направлении оси z (см. рис. 1).Так, например, для падающих волн напряжения и тока можно записать:

,

Коэффициент распространения волны в линии γ в общем случае является комплексной величиной и может быть представлен в виде:

,

где α — коэффициент затухания волны[5] в линии; β — коэффициент фазы[6]. Тогда соотношение (7) можно переписать в виде:

.

.

При этом фазовая скорость волны в линии VФ определяется через коэффициент фазы:

.

Сравнив коэффициенты при экспонентах с одинаковыми показателями степеней, получим:

,

где — волновое сопротивление линии[7].

Перепишем (6) с учетом (12):

.

Для определения коэффициентов A и B в этих уравнениях воспользуемся условиями в конце линии z = 0:

.

Тогда из (13) при z = 0 найдем

,

Подставив полученные значения коэффициентов из (14) в (13), после преобразований получим:

.

При выводе (15) учтены определения гиперболических синуса и косинуса[8].

Соотношения для напряжения и тока (15) так же, как и (6), являются решениями однородных волновых уравнений. Их отличие состоит в том, что напряжение и ток в линии в соотношении (6) определены через амплитуды падающей и отраженной волн, а в (15) — через напряжение и ток на нагрузке.

Рассмотрим простейший случай, когда напряжение и ток в линии определяются только падающей волной, а отраженная волна отсутствует[9]. Тогда в (6) следует положить BU = 0, BI = 0:

.

Распределение поля падающей волны

Рис.3. Эпюры напряжений падающей волны в длинной линии. а) амплитуда; б) фаза

На рис.3. представлены эпюры изменения амплитуды |U| и фазы φU апряжения вдоль линии. Эпюры изменения амплитуды и фазы тока имеют такой же вид. Из рассмотрения эпюр следует, что при отсутствии в линии потерь (α[5] = 0) амплитуда напряжения в любом сечении линии остается одной и той же. При наличии потерь в линии (α[5] > 0) часть переносимой мощности преобразуется в тепло (нагревание проводов линии и окружающего их диэлектрика). По этой причине амплитуда напряжения падающей волны экспоненциально убывает в направлении распространения.

Фаза напряжения падающей волны φU = β z изменяется по линейному закону и уменьшается по мере удаления от генератора.

Рассмотрим изменение амплитуды и фазы, например, напряжения при наличии падающей и отраженной волн. Для упрощения положим, что потери в линии отсутствуют, то есть α[5] = 0. Тогда напряжение в линии можно представить в виде:

,

где Γ = BU / AU — комплексный коэффициент отражения по напряжению.

Комплексный коэффициент отражения по напряжению

Характеризует степень согласования линии передачи с нагрузкой. Модуль коэффициента отражения изменяется в пределах:

| Г | = 0, если отражения от нагрузки отсутствуют и BU = 0[9]; | Г | = 1, если волна полностью отражается от нагрузки, то есть | AU | = | BU | ;

Соотношение (16) представляет собой сумму падающей и отраженной волн.

Рис.4. Векторная диаграмма напряжений в линии с отраженной волной

Отобразим напряжение на комплексной плоскости в виде векторной диаграммы, каждый из векторов которой определяет падающую, отраженную волны и результирующее напряжение (рис. 4). Из диаграммы видно, что существуют такие поперечные сечения линии, в которых падающая и отраженная волны складываются в фазе. Напряжение в этих сечениях достигает максимума, величина которого равна сумме амплитуд падающей и отраженной волн:

.

Кроме того, существуют такие поперечные сечения линии, в которых падающая и отраженная волны складываются в противофазе. При этом напряжение достигает минимума:

.

Рис.5. Эпюры распределения напряжения вдоль линии с отражённой волной. а) Модуль напряжения; б) фаза напряжения.

Напряжение в такой линии изменяется от нуля до удвоенной амплитуды падающей волны. На рис. 5 представлены эпюры изменения амплитуды и фазы напряжения вдоль линии при наличии отраженной волны.

Коэффициенты бегущей и стоячей волны

Эти коэффициенты, судя по определению, изменяются в пределах:

,

.

На практике наиболее часто используется понятие коэффициента стоячей волны, так как современные измерительные приборы (панорамные измерители kСВ) на индикаторных устройствах отображают изменение именно этой величины в определенной полосе частот.

Входное сопротивление длинной линии

Входное сопротивление линии — является важной характеристикой, которое определяется в каждом сечении линии как отношение напряжения к току в этом сечении:

Так как напряжение и ток в линии изменяются от сечения к сечению, то и входное сопротивление линии изменяется относительно ее продольной координаты z. При этом говорят о трансформирующих свойствах линии, а саму линию рассматривают как трансформатор сопротивлений. Подробнее свойство линии трансформировать сопротивления будет рассмотрено ниже.

Режимы работы длинной линии

Различают три режима работы линии:

режим бегущей волны; [10] режим стоячей волны; [10] режим смешанных волн.

Режим бегущей волны

Режим бегущей волны характеризуется наличием только падающей волны, распространяющейся от генератора к нагрузке. Отраженная волна отсутствует. Мощность, переносимая падающей волной, полностью выделяется в нагрузке. В этом режиме BU = 0, | Г | = 0, kбв =kсв = 1[10].

Режим стоячей волны

Режим стоячей волны характеризуется тем, что амплитуда отраженной волны равна амплитуде падающей BU = AU т. е. энергия падающей волны полностью отражается от нагрузки и возвращается обратно в генератор. В этом режиме, | Г | = 1, kсв = , kбв = 0[10].

Режим смешанных волн

В режиме смешанных волн амплитуда отраженной волны удовлетворяет условию 0 W Сопротивление нагрузки меньше волнового сопротивления линии RН

Источник