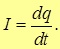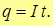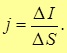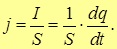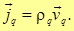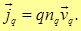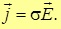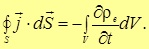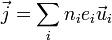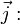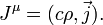что такое плотность электрического тока

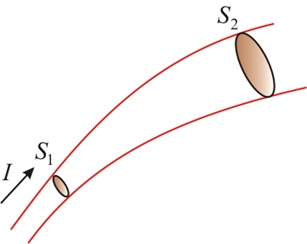
Сила и плотность тока. Линии тока

Сила тока I для тока, протекающего через некоторую площадь сечения проводника S эквивалентна производной заряда q по времени t и количественно характеризует электрический ток.

Электрический ток является процессом движения как отрицательных, так и положительных зарядов.

Перенос заряда одного знака в определенную сторону равен переносу заряда, обладающего противоположным знаком, в обратном направлении. В ситуации, когда ток образуется зарядами и положительного, и отрицательного знаков ( d q + и d q − ), справедливым будет заключение о том, что сила тока равна следующему выражению:

В качестве положительного определяют направление движения положительных зарядов. Ток может быть постоянным, когда ни сила тока, ни его направление не претерпевают изменений с течением времени, или, наоборот, переменным. При условии постоянства, формула силы тока может выражаться в следующем виде:

Плотность тока. Связь плотности тока с зарядом и силой тока, напряженностью

где j представляет собой модуль плотности электрического тока.

где j является модулем плотности электрического тока в проводнике, в котором заряд переносится электронами. В случае, если ток появляется как результат движения нескольких типов зарядов, то формула плотности тока может быть определена в виде следующего выражения:

Таким образом, плотность тока эквивалентна количеству электричества, другими словами заряду, который протекает за одну секунду через единицу сечения проводника. В отношении однородного цилиндрического проводника справедливым будет записать, что:

Основываясь на законе Ома для плотности токов можно записать такое выражение:

где λ обозначает коэффициент удельной электропроводности. Определив плотность тока, мы имеем возможность выразить силу тока в следующем виде:

Источник

4.1. Сила тока и плотность тока в проводнике

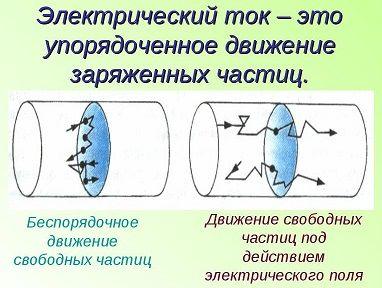
В проводниках часть валентных электронов не связана с определенными атомами и может свободно перемещаться по всему его объему. В отсутствие приложенного к проводнику электрического поля такие свободные электроны — электроны проводимости — движутся хаотично, часто сталкиваясь с ионами и атомами, и изменяя при этом энергию и направление своего движения. Через любое сечение проводника в одну сторону проходит столько же электронов, сколько и в противоположную. Поэтому результирующего переноса электронов через такое сечение нет, и электрический ток равен нулю. Если же к концам проводника приложить разность потенциалов, то под действием сил электрического поля свободные заряды в проводнике начнут двигаться из области большего потенциала в область меньшего — возникнет электрический ток. Исторически сложилось так, что за направление тока принимают направление движение положительных зарядов, которое соответствует их переходу от большего потенциала к меньшему.

Электрический ток характеризуется силой тока I (рис. 4.1).

Сила тока есть скалярная величина, численно равная заряду переносимому через поперечное сечение проводника в единицу времени

Рис. 4.1. Сила тока в проводнике

Согласно (4.1), сила тока в проводнике равна отношению заряда , прошедшего через поперечное сечение проводника за время к этому времени.

Замечание: В общем случае сила тока через некоторую поверхность равна потоку заряда через эту поверхность.

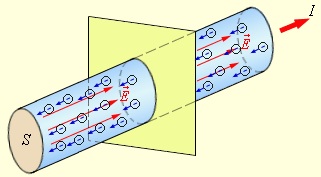
Если сила тока с течением времени не изменяется, то есть за любые равные промежутки времени через любое сечение проводника проходят одинаковые заряды, то такой ток называется постоянным, и тогда заряд, протекший за время t, может быть найден как (рис. 4.2)

Рис. 4.2. Постоянный ток, протекающий через разные сечения проводника

Величина 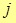, численно равная заряду, проходящему через единицу площади поперечного сечения проводника за единицу времени, называется плотностью тока.

С учетом определения силы тока плотность тока через данное сечение может быть выражена через силу тока , протекающего через это сечение

При равномерном распределении потока зарядов по всей площади сечения проводника плотность тока равна

В СИ единицей измерения силы тока является ампер (А). В СИ эта единица измерения является основной.

Уравнение (4.1) связывает единицы измерения силы тока и заряда

В СИ единицей измерения плотности тока является ампер на квадратный метр (А/м 2 ):

Это очень малая величина, поэтому на практике обычно имеют дело с более крупными единицами, например

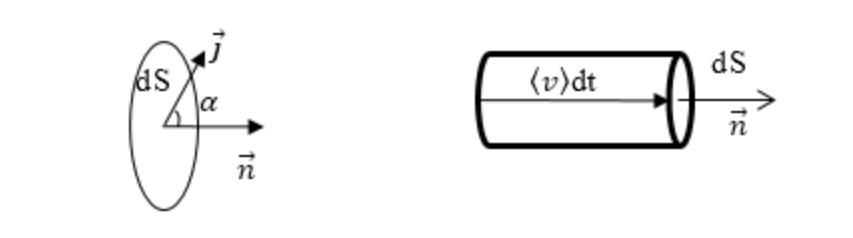
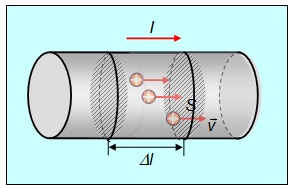
Плотность тока можно выразить через объемную плотность зарядов и скорость их движения v (рис. 4.3).

Рис. 4.3. К связи плотности тока j с объемной плотностью зарядов и дрейфовой скоростью v носителей заряда. За время dt через площадку S пройдут все заряды из объема dV = vdt S

Полный заряд, проходящий за время dt через некоторую поверхность S, перпендикулярную вектору скорости v, равен

Так как dq/(Sdt) есть модуль плотности тока j, можно записать

Поскольку скорость v есть векторная величина, то и плотность тока также удобно считать векторной величиной, следовательно

Здесь плотность заряда, скорость направленного движения носителей заряда.

Замечание: Для общности использован индекс , так как носителями заряда, способными участвовать в создании тока проводимости, могут быть не только электроны, но, например, протоны в пучке, полученном из ускорителя или многозарядные ионы в плазме, или так называемые «дырки» в полупроводниках «р» типа, короче, любые заряженные частицы, способные перемещаться под воздействием внешних силовых полей.

Кроме того, удобно выразить плотность заряда через число носителей заряда в единице объема — (концентрацию носителей заряда) . В итоге получаем:

Следует подчеркнуть, что плотность тока, в отличие от силы тока — дифференциальная векторная величина. Зная плотность тока, мы знаем распределение течения заряда по проводнику. Силу тока всегда можно вычислить по его плотности. Соотношение (4.4) может быть «обращено»: если взять бесконечно малый элемент площади , то сила тока через него определится как . Соответственно, силу тока через любую поверхность S можно найти интегрированием

Что же понимать под скоростью заряда v, если таких зарядов — множество, и они заведомо не движутся все одинаково? В отсутствие внешнего электрического поля, скорости теплового движения носителей тока распределены хаотично, подчиняясь общим закономерностям статистической физики. Среднее статистическое значение ввиду изотропии распределения по направлениям теплового движения. При наложении поля возникает некоторая дрейфовая скорость — средняя скорость направленного движения носителей заряда:

которая будет отлична от нуля. Проведем аналогию. Когда вода вырывается из шланга, и мы интересуемся, какое ее количество поступает в единицу времени на клумбу, нам надо знать скорость струи и поперечное сечение шланга. И нас совершенно не волнуют скорости отдельных молекул, хотя они и очень велики, намного больше скорости струи воды, как мы убедились в предыдущей части курса.

Таким образом, скорость в выражении (4.7) — это дрейфовая скорость носителей тока в присутствии внешнего электрического поля или любого другого силового поля, обуславливающего направленное (упорядоченное) движение носители заряда. Если в веществе возможно движение зарядов разного знака, то полная плотность тока определяется векторной суммой плотностей потоков заряда каждого знака.

Как уже указывалось, в отсутствие электрического поля движение носителей заряда хаотично и не создает результирующего тока. Если, приложив электрическое поле, сообщить носителям заряда даже малую (по сравнению с их тепловой скоростью) скорость дрейфа, то, из-за наличия в проводниках огромного количества свободных электронов, возникнет значительный ток.

Поскольку дрейфовая скорость носителей тока создается электрическим полем, логично предположить пропорциональность

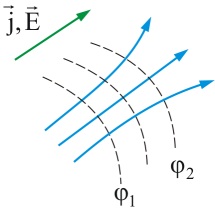
так что и плотность тока будет пропорциональна вектору напряженности (рис. 4.4)

Более подробно этот вопрос обсуждается в Дополнении

Входящий в соотношение (4.9)

Коэффициент пропорциональности 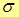называется проводимостью вещества проводника.

Проводимость связывает напряженность поля в данной точке с установившейся скоростью «течения» носителей заряда. Поэтому она может зависеть от локальных свойств проводника вблизи этой точки (то есть от строения вещества), но не зависит от формы и размеров проводника в целом. Соотношение (4.9) носит название закона Ома для плотности тока в проводнике (его называют также законом Ома в дифференциальной форме).

Рис. 4.4. Силовые линии электрического поля совпадают с линиями тока

Теперь получаем искомую оценку дрейфовой скорости электронов

Для сравнения: скорости хаотического теплового движения электронов при 20°С в меди по порядку величины составляют 10 6 м/с, то есть на одиннадцать порядков величины больше.

Возьмем произвольную воображаемую замкнутую поверхность S, которую в разных направлениях пересекают движущиеся заряды. Мы видели, что полный ток через поверхность равен

где dq — заряд, пересекающий поверхность за время dt. Обозначим через q ‘ заряд, находящийся внутри поверхности. Его можно выразить через плотность заряда , проинтегрированную по всему объему, ограниченному поверхностью

Подставляя сюда написанные выше выражения для скоростей изменения заряда внутри поверхности , получаем математическое соотношение, выражающее закон сохранения заряда в интегральной форме

Напомним, что интегрирования ведутся по произвольной поверхности S и ограниченному ею объему V.

Источник

Плотность электрического тока

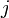
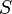
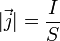
Плотность то́ка — векторная величина, имеющая смысл силы тока, протекающего через единицу площади. Например, при равномерном распределении плотности тока по сечению проводника .

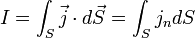
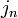
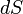
В общем случае, , где — нормальная (ортогональная) составляющая вектора плотности тока по отношению к элементу площади .

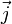
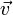
Направление вектора соответствует направлению вектора скорости , с которой движутся заряды, создающие ток, в предположении, что заряды положительны. В сложных системах (с различными типами носителей заряда, например, в плазме)

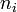
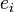
Для всех типов подвижных носителей заряда, сумма концентраций частиц данного типа (), домноженных на заряд одной частицы данного типа () и на среднюю скорость частиц этого типа.

4-вектор плотности тока

В теории относительности вводится четырёхвектор плотности тока (4-ток), составленный из объёмной плотности заряда ρ и 3-вектора плотности тока

Это позволяет записывать уравнения электродинамики в ковариантном виде.

См. также

Полезное

Смотреть что такое «Плотность электрического тока» в других словарях:

ПЛОТНОСТЬ ЭЛЕКТРИЧЕСКОГО ТОКА — векторная характеристика тока, равная по модулю электрич. заряду, проходящему за единицу времени через единичную площадку, перпендикулярную направлению упорядоченного движения заряж. ч ц. Если плотность заряда (заряд в единице объёма) r, то П. э … Физическая энциклопедия

плотность электрического тока — плотность электрического тока; плотность полного тока Векторная величина, равная сумме плотности тока проводимости, плотности тока переноса и плотности тока смещения … Политехнический терминологический толковый словарь

плотность электрического тока — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN current densityCD … Справочник технического переводчика

плотность (электрического) тока — 52 плотность (электрического) тока Векторная величина, равная сумме плотности электрического тока проводимости, плотности электрического тока переноса и плотности электрического тока смещения Источник: ГОСТ Р 52002 2003: Электротехника. Термины и … Словарь-справочник терминов нормативно-технической документации

плотность электрического тока — elektros srovės tankis statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. areic electric current; electric current density vok. elektrische Stromdichte, f rus.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

плотность электрического тока — elektros srovės tankis statusas T sritis Standartizacija ir metrologija apibrėžtis Elektros srovės stipris vienetiniame plote. Matavimo vienetas: A/m². atitikmenys: angl. areic electric current; electric current density vok. elektrische… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

плотность электрического тока — elektros srovės tankis statusas T sritis Standartizacija ir metrologija apibrėžtis Vektorius, kurio skaitinė vertė lygi krūviui, pereinančiam per vienetinį laiko tarpą per vienetinio ploto paviršių, statmeną elektringųjų dalelių (krūvininkų)… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

плотность электрического тока — elektros srovės tankis statusas T sritis fizika atitikmenys: angl. electric current density vok. elektrische Stromdichte, f rus. плотность электрического тока, f pranc. densité de courant électrique, f … Fizikos terminų žodynas

Плотность (электрического) тока — 1. Векторная величина, равная сумме плотности электрического тока проводимости, плотности электрического тока переноса и плотности электрического тока смещения Употребляется в документе: ГОСТ Р 52002 2003 Электротехника. Термины и определения… … Телекоммуникационный словарь

Источник

Плотность тока формула

Электрическое поле воздействует на заряды, в результате, они начинают упорядоченно перемещаться. Такое перемещение получило определение электрического тока. Как правило, заряды двигаются в какой-либо среде, называемой проводником, и являются носителями тока. Одной из основных характеристик движения зарядов является плотность тока, формула которого описывает электрический заряд, переносимый за 1 секунду через сечение проводника, которое перпендикулярно направлению этого тока.

Чем определяется плотность тока

Понятие плотности тока определяется количеством электричества, протекающим через сечение проводника в течение одной секунды. Направление электротока является перпендикулярным сечению проводника.

Если взять однородный проводник цилиндрической формы, в котором ток имеет равномерное распределение по всему сечению, то его плотность будет выражаться в виде формулы: J = I / S, где I является силой тока, а S – площадью поперечного сечения. Единицей измерения этой величины служит А/м2 (ампер на метр квадратный). Данная величина является векторной. Ее направление совпадает с направлением напряженности электрического поля.

Использование плотности тока на практике

Очень часто возникает вопрос о возможности использования конкретного провода для тех или иных целей. То есть, способен ли он выдержать определенную нагрузку. В этих случаях, очень важно определить плотность электротока с допустимой величиной.

Данный показатель очень важен, поскольку в каждом проводнике возникает сопротивление току, протекающему через него. Происходят потери тока, из-за чего проводник начинает нагреваться. При слишком больших потерях, наступает критическое нагревание, вызывающее расплавление проводника. Чтобы исключить подобные ситуации, каждому прибору или потребителю устанавливается наиболее оптимальная плотность тока, формула которой позволит рассчитать нужное сечение провода.

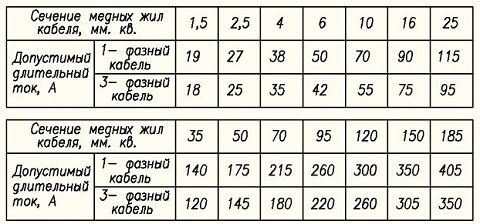
Когда возникает необходимость выбрать нужное сечение провода или кабеля, необходимо учитывать допустимое значение плотности электротока. Для практических расчетов во время проектирования используются специальные таблицы и формулы, позволяющие получить желаемый результат.

Для разных металлов существуют различные значения плотности. В настоящее время используются только медные провода, в которых плотность электротока не должна превышать 6-10 А/мм2. Это особенно актуально для долговременной эксплуатации, когда проводке обеспечивается облегченный режим. Допускается эксплуатация и при повышенных нагрузках, только на очень короткое время.

Что такое плотность тока

Формула для закона Ома

Плотность энергии магнитного поля

Формула удельного сопротивления

Правило левой руки: применение правила Буравчика, формулы, примеры задач

Источник