что такое плоскость симметрии фигуры
Презентация по геометрии » Симметрия относительно плоскости»
Ищем педагогов в команду «Инфоурок»
Описание презентации по отдельным слайдам:
«Симметрия…есть идея, с помощью которой человек веками пытался объяснять и создавать порядок, красоту и совершенство» ( Герман Вейль)
История симметрии Однако как люди дошли до такой сложной и одновременно такой простой вещи, как симметрия? Ещё древние греки считали, что симметрия – это гармония, соразмерность. Они же и ввели термин συμμετρία, который сейчас перешёл в русское слово «симметрия» А у древних народов, таких как шумеры и египтяне, у первобытных племён, да и у кое-кого в наше время симметрия ассоциируется не только с красотой и гармонией, но и прежде всего с магией. Не зря же люди в эпоху мегалита для ритуальных целей сооружали кромлихи в форме круга – «идеально симметричной» геометрической фигуры.
Вспомогательные образы (плоскости, точки, прямые и т.д.), с помощью которых устанавливается симметрия, называются элементами симметрии.
Симметричные фигуры В трехмерном мире пространственных тел, где мы с вами живем, существуют плоскости симметрии. При взгляде на круглые тела сразу видно, что они имеют плоскости симметрии, но вот сколько именно — решить не всегда просто. На плоскости фигурой с бесчисленным множеством осей симметрии был круг. Поэтому нас не должно удивлять, что в. пространстве аналогичные свойства присущи шару. Но если круг является единственным в своем роде, то в трехмерном мире имеется целый ряд тел, обладающих бесконечным множеством плоскостей симметрии: прямой цилиндр с кругом в основании, конус с круговым или полусферическим основанием, шар или сегмент шара. Или возьмем примеры из жизни: сигарета, сигара, стакан, конусообразный фунтик с мороженым, кусочек проволоки, труба.
Элементы симметрии: Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.
Симметрия встречается в физике, биологии, в архитектуре, в религии и искусстве
Симметрия в природе
Симметрия в архитектуре
Симметрия в одежде
Симметрия в архитектуре г. Санкт- Петербурга Александринский театр Исаакиевский собор
Улица Росси имеет плоскость симметрии в общем обзоре, но не все детали в архитектуре зданий симметричны.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Номер материала: ДБ-070120
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
В Минпросвещения предложили организовать телемосты для школьников России и Узбекистана
Время чтения: 1 минута
Путин попросил привлекать родителей к капремонту школ на всех этапах
Время чтения: 1 минута
В Москве запустили онлайн-проект по борьбе со школьным буллингом
Время чтения: 2 минуты
В российских школах оборудуют кабинеты для сообщества «Большой перемены»
Время чтения: 1 минута
Минпросвещения будет стремиться к унификации школьных учебников в России
Время чтения: 1 минута
Российские адвокаты бесплатно проконсультируют детей 19 ноября
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Осевая и центральная симметрия
Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.
Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
Рассмотрите фигуры с осевой и центральной симметрией.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Осевая симметрия
Вот как звучит определение осевой симметрии:
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.
При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.
В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.
Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.
Центральная симметрия
Теперь поговорим о центральной симметрии — вот ее определение:
Центральной симметрией называется симметрия относительно точки.
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах на 8 марта.
Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.
Пример 2. Постройте треугольник A1B1C1, симметричный треугольнику ABC, относительно центра (точки О).
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно центра (точки О).
Задачи на самопроверку
В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.
Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:
Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная
Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М1 и N1 — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М1N1.
Подсказка: опустите перпендикуляры из точек N и N1 на прямую MМ1.
Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.
Что такое плоскость симметрии фигуры
Итак, что касается геометрии: выделяют три основных вида симметрии.
Во-первых, центральная симметрия (или симметрия относительно точки) – это преобразование плоскости (или пространства), при котором единственная точка (точка О – центр симметрии) остаётся на месте, остальные же точки меняют своё положение: вместо точки А получаем точку А1 такую, что точка О середина отрезка АА1. Чтобы построить фигуру Ф1, симметричную фигуре Ф относительно точки О, нужно через каждую точку фигуры Ф провести луч, проходящий через точку О (центр симметрии), и на этом луче отложить точку, симметричную выбранной относительно точки О. Множество построенных таким образом точек даст фигуру Ф1.
Большой интерес вызывают фигуры, имеющие центр симметрии: при симметрии относительно точки О любая точка фигурф Ф преобразуется опять же в некоторую точку фигуры Ф. Таких фигур в геометрии встречается много. Например: отрезок (середина отрезка – центр симметрии), прямая (любая её точка – центр её симметрии), окружность (центр окружности – центр симметрии), прямоугольник (точка пересечения его диагоналей – центр симметрии). Много центральносимметричных объектов в живой и неживой природе (сообщение учащихся). Часто люди сами создают объекты, имеющие центр симмет рии (примеры из рукоделия, примеры из машиностроения, примеры из архитектуры и много других примеров).
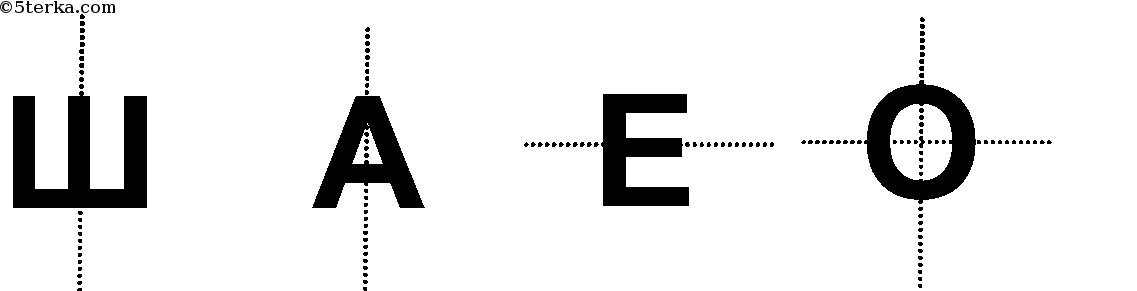
Чтобы построить фигуру Ф1,симметричную фигуре Ф относительно плоскости α, нужно для каждой точки фигуры Ф выстроить симметричные относительно α точки, они в своём множестве и образуют фигуру Ф1.
Материал к уроку геометрии «Симметрия в пространстве», 10 класс
Ищем педагогов в команду «Инфоурок»
Выбранный для просмотра документ Симметрия в пространстве УРОК.doc
Федеральное государственное бюджетное образовательное учреждение
«Всероссийский детский центр «Океан»
Конкурс « XXI век – торжество информационных технологий»
«Симметрия в пространстве. Элементы симметрии правильных многогранников»
ФИО конкурсанта: Скворцова
Наталья Вячеславна, учитель математики
Тип урока: комбинированный
Продолжительность: 45 мин.
г. Владивосток, 2012 г.
Цель: ознакомить учащихся с симметрией и ее видами в пространстве.
ознакомить учащихся с основными видами симметрии в пространстве и её элементами;
показать возможности использования понятия «симметрия» в математике, химии, физике, биологии.
развивать познавательную активность и творческие способности;
активизировать самостоятельную деятельность.
воспитывать коммуникативность учащихся.
Компьютер, видеопроектор, электронная доска, О MS Module file «Оси и плоскости симметрии», презентация «Элементы симметрии правильных многогранников», демонстрационные модели многогранников, доска меловая, чертёжные инструменты.
Организационный момент (3 мин)
Изучение нового материала (5 мин) + Практикум (5 мин)
Использования понятия «симметрия» в других областях (5 мин)
Фронтальный опрос (3 мин) +Симметрия куба – демонстрация (4 мин)
Закрепление нового материала (5 мин)
Проверочная работа (7 +1мин)
Итог урока (рефлексия) (4 мин)
«Раз, стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия приятна для глаз? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно основано? Разве во всём в жизни есть симметрия?»
Л. Толстой «Отрочество»
Организационный момент: откройте тетради, запишите сегодняшнее число и тему урока
Сообщение темы, целей урока.
Вводное слово учителя.
Понятие симметрии проходит через всю многовековую историю человеческого творчества.
Изучение нового материала (Слайд)
Новый словарь русского языка Т.Ф.Ефремовой:
Толковый словарь русского языка Д.Н.Ушакова:
П
1
1б) Точка О считается симметричной самой себе. (Слайд)
2
2
3а) Точки А и А1 называются симметричными относительно плоскости (плоскость симметрии), если эта плоскость проходит через середину отрезка АА1 и перпендикулярна этому отрезку.
3б) Каждая точка плоскости считается симметричной самой себе. (Слайд)
Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры.
Если фигура имеет центр (ось, плоскость) симметрии, то говорят, что она обладает центральной (осевой, зеркальной) симметрией. (Слайд с анимацией)
Задание (работа 3 учеников у доски, остальные учащиеся выполняют работу в тетрадях):
Сколько осей симметрии имеют каждая из фигур? (Множество, три, ни одной)
Начертите окружность, правильный треугольник и многоугольник используя осевую и центральную симметрию.
Я предлагаю вам рассмотреть проявление этой идеи в различных областях науки.
Симметрия в физике и технике (Слайд)
Взаимосвязь электрического и магнитного полей. В 1894 г. на свет появилась последняя работа Пьера Кюри, посвящённая симметрии физических явлений. Статья называлась «О симметрии физических явлений: симметрия электрического и магнитного поля».
С
Симметрия обнаруживается также и на атомном уровне изучения вещества. Она проявляется в недоступных непосредственному наблюдению геометрически упорядоченных атомных структурах молекул.
Симметрия в биологии. (Слайд)
Н
С
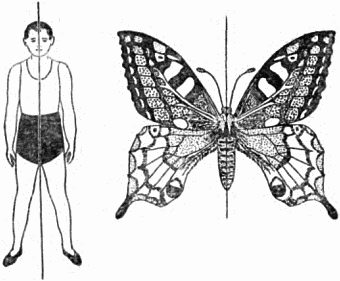
Симметрия у человека.
Тело человека построено по принципу двусторонней симметрии.
Обладает ли симметрией лицо человека? (Слайд)
– 
Фронтальный опрос (повторение)
Что называют многогранником? Поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело. (Слайд)
Какой многогранник называется правильным?
Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники и в каждой его вершине сходится равное число ребер.
К
Д
З 
ЗАДАНИЕ 1: Какой из представленных физических приборов обладает осевой симметрией? (Ответ: весы)
З 
ЗАДАНИЕ 3: Определите (и покажите) количество осей симметрии изображения. (Ученик на доске проводит 5 осей симметрии)
ЗАДАНИЕ 4-6: О MS Module file «Оси и плоскости симметрии» (Ученик у доски)
Проверочная работа с взаимопроверкой (7 мин + 1 мин)
Итог урока. Рефлексия. (4 мин)
Учитель озвучивает домашнее задание, оценки за устную работу на уроке. Работу на уроке каждого, определяет проверочная работа. Спасибо за урок, до свидания!
Атанасян Л.С., Бутузов В.Ф и др. Геометрия 10-11: базовый и профильный уровни – М.: Просвещение, 2010
Смирнова И.М. В мире многогранников. М., 1990.
Шафрановский И.И. Симметрия в природе. Л., 1988.
Геометрия. 11 класс
Конспект урока
Геометрия, 11 класс
Урок №4. Движения в пространстве
Перечень вопросов, рассматриваемых в теме:
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 121-126.
Шарыгин И.Ф. Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 178-196.
Потоскуев Е.В., Звавич Л. И., Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-63.
Открытые электронные ресурсы:
Теоретический материал для самостоятельного изучения
1. Определение движения в пространстве
Преобразованием пространства называется взаимно-однозначное отображение пространства на себя.
Два преобразования называются равными, если образы любой точки при этих преобразованиях совпадают.
Точка А называется неподвижной точкой при некотором преобразовании f, если при этом преобразовании она отображается на себя.
Фигура F называется неподвижной фигурой при некотором преобразовании f, если при этом преобразовании она отображается на себя.
Преобразование пространства, которое каждую точку отображает на себя, называется тождественным преобразованием. Оно обычно обозначается Е. При тождественном преобразовании все точки и все фигуры пространства являются неподвижными.
Для любых двух преобразований можно рассмотреть третье, которое получается последовательным применением этих преобразований. Например, если преобразование f отображает точку М на точку М’, а преобразование g отображает точку М’ на точку M», то преобразование f°g отображает точку М на точку M»: f°g(М)=g(f(M))=M».
Под движением пространства понимается отображение пространства на себя, при котором любые две точки A и B переходят (отображаются) в некие точки A1 и B1 так, что |AB|=|A1B1|.
Иными словами, движение пространства — это отображение пространства на себя, сохраняющее расстояния между точками. Так же, как и для движения на плоскости, можно доказать, что при движении в пространстве
— прямые переходят в прямые,
— полупрямые — в полупрямые,
— отрезки — в отрезки,
— сохраняются углы между прямыми.
Новое свойство движения в пространстве: движение переводит плоскости в плоскости.
В пространстве, так же как и на плоскости, две фигуры называются равными, если они совмещаются движением.
Можно доказать, что композиция двух движений пространства есть движение.
Центральная симметрия в пространстве задается и определяется так же, как и на плоскости
Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно точки O, называется центральной симметрией пространства относительно точки O. При этом точка O отображается на себя и называется центром симметрии.
Рисунок 1 – Центральная симметрия
На рисунке точка О – центр симметрии, АО=А1О, ВО=В1О, СО=С1О, DО=D1О (по определению точки, симметричной данной).
Центральная симметрия имеет только одну неподвижную точку – центр симметрии.
Сформулируем некоторые свойства центральной симметрии:
1) Прямая, проходящая через центр симметрии, отображается на себя.
2) Прямая, не проходящая через центр симметрии, отображается на параллельную ей прямую.
3) Плоскость, проходящая через центр симметрии, отображается на себя (то есть является неподвижной плоскостью этой центральной симметрии).
4) Плоскость, не проходящая через центр симметрии, отображается на параллельную ей плоскость.
3. Осевая симметрия (симметрия относительно прямой):
Точка M’ пространства, не лежащая на прямой m, называется симметричной точке М относительно прямой m, если отрезок ММ’ перпендикулярен этой прямой и делится ею пополам.
Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно прямой m, называется осевой симметрией пространства относительно прямой m. Прямая m отображается на себя и называется осью симметрии.
Рисунок 2 – Осевая симметрия
Неподвижные прямые осевой симметрии:
2) любая прямая, перпендикулярная прямой m
Неподвижные плоскости осевой симметрии:
1) любая плоскость, проходящая через прямую m
2) любая плоскость, перпендикулярная прямой m.
Зеркальная симметрия (симметрия относительно плоскости):
Точка M’ пространства, не лежащая на плоскости α, называется симметричной точке М относительно плоскости α, если отрезок ММ’ перпендикулярен этой плоскости и делится ею пополам.
Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно плоскости α, называется зеркальной симметрией пространства относительно плоскости α. Плоскость α отображается на себя и называется плоскостью симметрии.
Рисунок 3 – Зеркальная симметрия
Неподвижные прямые зеркальной симметрии:
1) любая прямая плоскости α
2) любая прямая, перпендикулярная плоскости α
Неподвижные плоскости зеркальной симметрии:
1) сама плоскость α
2) любая плоскость, перпендикулярная плоскости α.
Параллельный перенос (точки переносятся на данный вектор):
Рисунок 4 – параллельный перенос
Пусть дан вектор 
Преобразование пространства, при котором каждая точка пространства M, отображается на такую точку M’, что выполняется равенство 

Перенос на нулевой вектор 
Параллельный перенос отображает прямую на параллельную ей прямую либо на себя; плоскость на параллельную ей плоскость либо на себя.
Неподвижных точек параллельный перенос на ненулевой вектор не имеет.
Неподвижными прямыми при параллельном переносе на вектор 
Неподвижными плоскостями при параллельном переносе на вектор 
Поворот на данный угол вокруг данной оси:
Поворотом пространства на угол φ вокруг прямой n называется такое преобразование пространства, при котором любая точка прямой остается неподвижной и в любой плоскости, перпендикулярной прямой n, осуществляется поворот этой плоскости на угол φ вокруг точки ее пересечения с прямой n.
Рисунок 5 – Поворот вокруг прямой
Неподвижными точками являются любая точка оси вращения.
Неподвижной прямой является ось поворота.
Неподвижной плоскостью является любая плоскость, перпендикулярная оси поворота.
Поворот вокруг оси на угол 180 0 является осевой симметрией.
Примеры и разбор решения заданий тренировочного модуля
Дан треугольника АВС: А(3,- 2, 4), В (4, 6, 0), С (2, 2, 2)
В какую точку перейдет центр О пересечения медиан данного треугольника при:
Симметрия относительно начала координат
Симметрия относительно координатной плоскости ZOY
Поворот на угол 180 0 относительно координатной оси OZ
Симметрия относительно плоскости х=2
Найдем точку пересечения медиант данного треугольника.
М (
Так как медианы треугольника пересекаются в одной точке и делятся в отношении 2:1, считая от вершины, то можем найти координаты точки О, зная координаты А и М:
Теперь найдем координаты образа точки О при каждом из преобразований:.


Эта плоскость параллельная плоскости ZOY, поэтому ордината и аппликата точки остаются такими же. Так как абсцисса токи О хо =3, то расстояние от точки до плоскости α равно 1. Точка, симметричная точке О относительно плоскости α, будет иметь абсциссу, равную хо’ =1.

























