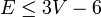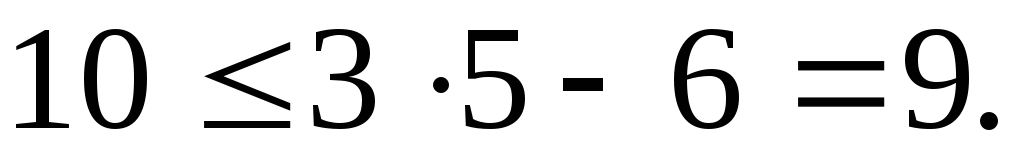что такое планарный граф

Планарность

Планарный граф — граф, который может быть изображен на плоскости без пересечения ребер.

Более строго: Граф укладывается на некоторой поверхности, если его можно на ней нарисовать без пересечения ребер. Уложенный граф называется геометрическим, его вершины это точки плоскости, а ребра линии на ней, области, на которые граф разбивает поверхность называются гранями. Плоский граф — граф уложенный на плоскость. Граф называется планарным, если он изоморфен некоторому плоскому графу.

Содержание

Критерий непланарности

Теорема Понтрягина-Куратовского

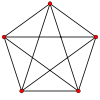
Граф планарен тогда и только тогда, когда не содержит подграфов, гомеоморфных K₅ или K_3,3.

Граф планарен тогда и только тогда, когда он не содержит подграфов, стягиваемых в K₅ или K_3,3.

Формула Эйлера

Для связного плоского графа справедливо следующее соотношение между количеством вершин V, ребер E и граней F:

Оно было найдено Эйлером в 1736 г. [1] при изучении свойств выпуклых многогранников. Это соотношение справедливо и для других поверхностей с точностью до коэффициента, называемого эйлеровой характеристикой. Это инвариант поверхности, для плоскости или сферы он равен двум.

Формула имеет множество полезных следствий. Из того, что каждая грань ограничена не более чем тремя ребрами, следует, что для плоского графа

то есть, при большем числе ребер граф заведомо непланарен. (Обратное утверждение не верно, пример.) Отсюда следует, что в планарном графе всегда можно найти вершину степени не более 5.

Планарные графы в задачах

Задача о трех колодцах. Есть три дома и три колодца. Доказать, что невозможно так проложить дорожки между домами и колодцами, чтобы от каждого дома к каждому колодцу вела дорожка, и никакие две дорожки не пересекались бы. (Мосты строить нельзя.)

Раскраска карты. Необходимо раскрасить плоскую карту заданным числом красок так, что любые две страны имеющий общий участок границы имели различные цвета. Оказывается, что при отсутствии анклавов, всегда достаточно четырех красок, но это утверждение чрезвычайно сложно доказать, см. Проблема четырёх красок.

См. также

Примечания

Ссылки

Полезное

Смотреть что такое «Планарность» в других словарях:

Киприанов, Андрей Иванович — [р. 4 (16) июля 1896] сов. химик органик, акад. АН УССР (с 1945). В 1919 окончил Харьков. ун т, где работал до 1941 (с 1940 проф.). С 1944 проф. Киев. ун та; одновременно (с 1945) дир. Ин та органич. химии АН УССР. Осн. работы выполнены в области … Большая биографическая энциклопедия

ИНТЕГРАЛЬНАЯ СХЕМА — твердотельное устройство, содержащее группу приборов и их соединения (связи), выполненное на единой пластине (подложке). В И. с. интегрируются пассивные элементы (ёмкости, сопротивления) и активные элементы, действие к рых основано на разл. физ.… … Физическая энциклопедия

ГИПЕРГРАФ — обобщение понятия графа. Г. задается множеством V, элементы к рого наз. вершинами, и семейством подмножеств множества V, называемых ребрами Г.; Г. обозначается Понятие Г. является вариантом давно известных понятий комплекса, блок схемы, а также… … Математическая энциклопедия

Теория графов — Граф с шестью вершинами и семью рёбрами Теория графов раздел дискретной математики, изучающий свойства графов. В общем смысле граф представляется как множество вершин (узлов), соединённых рёбрами. В строго … Википедия

Планарный граф — Планарный граф граф, который может быть изображен на плоскости без пересечения ребер. Более строго: Граф укладывается на некоторой поверхности, если его можно на ней нарисовать без пересечения ребер. Уложенный граф называется геометрическим … Википедия

Гамма-алгоритм — Гамма алгоритм алгоритм плоской укладки графа и проверки его на планарность. Содержание 1 Определения 2 Алгоритм 3 Реализация … Википедия

Гипотеза Хадвигера — Не следует путать с проблемой Нелсона Эрдеша Хадвигера. Гипотеза Хадвигера одна из неразрешённых гипотез теории графов. Она формулируется следующим образом: всякий k хроматический граф стягиваем к полному графу на вершинах.… … Википедия

Система графов — Системой графов является такая совокупность или множество графов, где между элементами зафиксировано соотношение. Графы систематизируются исходя из характеристик, чаще всего, таких как планарность, регулярность, транзитивность и т.д. Большая… … Википедия

Источник

П.11. Планарные графы.

11.1. Планарные графы.

Графы, которые рассматривались выше, изображали на плоскости, где вершинами являются точки плоскости, а ребра – непрерывные плоские линия. Среди многих прикладных задач из теории графов интерес представляют те, которые можно изобразить на плоскости так, чтобы их ребра не пересекались.

Вот, например, некоторые прикладные задачи. Интегральная микросхема состоит из слоев миниатюрных микросхем, впечатанных в пластину. В такой ситуации крайне важно исключить пересечение проводов в местах, не предназначенных для соединений. Если изобразить места указанных соединений вершинами графа, то возникает задача построения графа с непересекающимися ребрами. Аналогичная задача возникает при проектировании железнодорожных и других путей, где нежелательны переезды.

Но надо подчеркнуть, что нас интересует возможностьпостроения графа с непересекающимися ребрами.

Определение 11.1. Планарным графом называется граф, который может быть изображен на плоскости, так что его ребра не пересекаются.

Все планарные графы укладываются на плоскости (имеют плоскую укладку).

1) Всякий подграф планарного графа планарен.

2) Граф планарен тогда и только тогда, когда каждая связная компонента этого графа – планарный граф.

Рассмотрим граф как рисунок, изображенный на листе бумаги. Если граф планарен и нарисован так, что никакие линии не пересекаются, и его необходимо разрезать вдоль ребер, то граф окажется разделенным на части, включая внешнюю часть. Такие части называются гранями. Заметим, что границы каждой грани являются циклом.

Определение 11.2.Граньюпланарного графа называется множество точек плоскости, каждая из которых может быть соединена плоской кривой, не пересекающей ребер графа.Границейграни называется множество вершин и ребер, принадлежащих этой грани.

Теорема 11.1.(теорема Эйлера) ЕслиG– связный планарный граф, содержащийvвершин,eребер иfграней, то

(11.1.1)

Пусть G– связный планарный граф, который имеетvвершин. Рассмотрим некоторый остовэтого графа. Остов имеет всего одну внешнюю грань,vвершин иребер, т.е.,и. Значит,. Формула (11.1.1) для остовавыполняется.

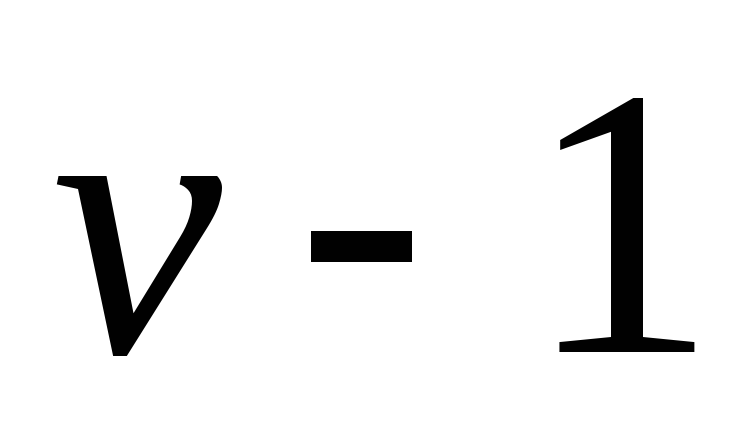
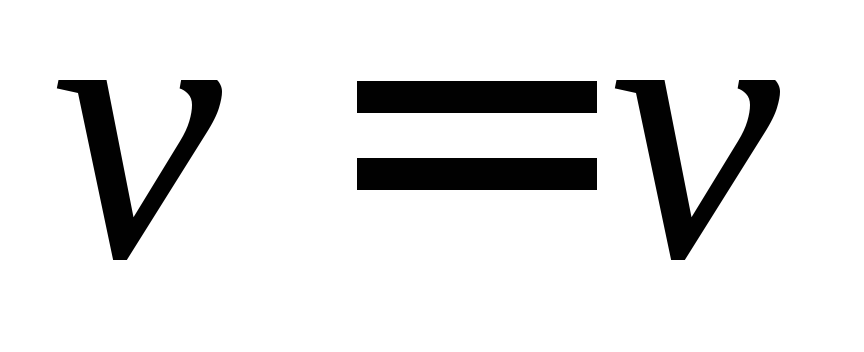
Будем поочередно добавлять к остову недостающие ребра графаG. При каждом добавлении число вершин не изменится, число ребер увеличивается на единицу, так же как и число граней, поскольку при добавлении к остову ребра, связывающего две несмежные вершины, получается цикл, разделяющий текущую грань на две.

Таким образом, формула (11.1.1) будет верна для всякого графа, получающегося в результате таких операций, а поскольку графом Gзаканчивается вся эта процедура, то эта формула будет верна и для него.

Пример 1.3.Планарный граф имеет вершины со степенями 2, 2, 2, 3, 3, 3, 4, 4, 4 и 5, соответственно. Сколько у него ребер и граней?

Решение.Всего вершин 10, т.е.. Найдем сумму степеней вершин графа. Значит, число ребер равно(по теореме Эйлера о сумме степеней вершин графа). Тогда число граней.

Источник

Планарный граф

Связанные понятия

В теории графов неориентированный граф H называется минором графа G, если H может быть образован из G удалением рёбер и вершин и стягиванием рёбер.

В теории графов графом-циклом называется граф, состоящий из единственного цикла, или, другими словами, некоторого числа вершин, соединённых замкнутой цепью. Граф-цикл с n вершинами обозначают как Cn. Число вершин в Cn равно числу рёбер и каждая вершина имеет степень 2, то есть любая вершина инцидентна ровно двум рёбрам.

Кликой неориентированного графа называется подмножество его вершин, любые две из которых соединены ребром. Клики являются одной из основных концепций теории графов и используются во многих других математических задачах и построениях с графами. Клики изучаются также в информатике — задача определения, существует ли клика данного размера в графе (Задача о клике) является NP-полной. Несмотря на эту трудность, изучаются многие алгоритмы для поиска клик.

В теории графов outerplanar graph — это граф, допускающий планарную диаграмму, в которой все вершины принадлежат внешней грани.

В теории графов рёберным графом L(G) неориентированного графа G называется граф L(G), представляющий соседство рёбер графа G.

Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице).

В теории графов совершенным графом называется граф, в котором хроматическое число любого порождённого подграфа равно размеру максимальной клики этого подграфа. Благодаря строгой теореме о совершенных графах, с 2002 года известно, что совершенные графы — это то же самое, что и графы Бержа. Граф G является графом Бержа если ни G, ни его дополнение не имеет порождённых циклов нечётной длины (5 и более рёбер).

В теории графов вершиной называется фундаментальная единица, образующая графы — неориентированный граф состоит из множества вершин и множества рёбер (неупорядоченных пар вершин), в то время как ориентированный граф состоит из множества вершин и множества дуг (упорядоченных пар вершин). На рисунках, представляющих граф, вершина обычно обозначается кружком с меткой, ребро — линией, дуга — стрелкой, соединяющей вершины.

В теории графов графом пересечений называется граф, представляющий схему пересечений семейства множеств. Любой граф можно представить как граф пересечений, но некоторые важные специальные классы можно определить посредством типов множеств, используемых для представления в виде пересечений множеств.

В теории графов графом гиперкуба Qn называется регулярный граф с 2n вершинами, 2n−1n рёбрами и n рёбрами, сходящимися в одной вершине. Его можно получить как одномерный скелет геометрического гиперкуба. Например, Q3 — это граф, образованный 8 вершинами и 12 рёбрами трёхмерного куба. Граф можно получить другим образом, отталкиваясь от семейства подмножеств множества с n элементами путём использования в качестве вершин все подмножества и соединением двух вершин ребром, если соответствующие множества.

В теории графов графом единичных расстояний называется граф, образованный точками на евклидовой плоскости, при этом две вершины соединяются ребром если расстояние между ними равно в точности единице. Рёбра графа единичных расстояний иногда пересекаются, так что они не всегда планарны. Граф единичных расстояний без пересечений называется спичечным графом.

В теории графов говорят, что граф G гипогамильтонов, если сам по себе граф не имеет гамильтонова цикла, но любой граф, полученный удалением одной вершины из G, является гамильтоновым.

В теории графов графом без клешней называется граф, который не содержит порождённых подграфов, изоморфных K1,3 (клешней).

Источник

СОДЕРЖАНИЕ

Теоремы Куратовского и Вагнера

Вместо того, чтобы рассматривать подразделения, теорема Вагнера имеет дело с несовершеннолетними :

Минор графа результатов принимать подграф и неоднократно стягивание края в вершину, с каждым соседом исходных конечных вершин становится соседом новой вершины.

Другие критерии планарности

На практике трудно использовать критерий Куратовского, чтобы быстро решить, является ли данный граф плоским. Однако существуют быстрые алгоритмы решения этой проблемы: для графа с n вершинами можно определить за время O ( n ) (линейное время), может ли граф быть плоским или нет (см. Проверка планарности ).

Для простого связного плоского графа с v вершинами, e ребрами и f гранями для v ≥ 3 выполняются следующие простые условия :

Формула Эйлера

Средняя степень

Графики монет

Плотность планарного графика

Связанные семейства графов

Максимальные плоские графы

Внешнепланарные графы

Графики Халина

Другие родственные семьи

Перечисление планарных графов

Почти все плоские графы имеют экспоненциальное число автоморфизмов.

Другие факты и определения

Теорема о четырех цветах утверждает, что каждый планарный граф можно раскрашивать в четыре цвета (т. Е. С четырьмя частями).

Двойственные полезны, потому что многие свойства двойственного графа связаны простыми способами со свойствами исходного графа, что позволяет доказывать результаты о графах, исследуя их двойственные графы.

Хотя дуальный, построенный для конкретного вложения, уникален (с точностью до изоморфизма ), графы могут иметь разные (т. Е. Неизоморфные) дуальные, полученные из разных (т. Е. Негомеоморфных ) вложений.

Теорема о плоском разделителе утверждает, что любой планарный граф с n вершинами можно разбить на два подграфа размером не более 2 n / 3 путем удаления O ( √ n ) вершин. Как следствие, планарные графы также имеют ширину дерева и ширину ветвления O ( √ n ).

Для двух плоских графов с v вершинами можно определить за время O ( v ), изоморфны они или нет (см. Также проблему изоморфизма графов ).

Представимые в виде слов плоские графы включают в себя плоские графы без треугольников и, в более общем смысле, трехцветные плоские графы, а также определенные подразделения граней треугольных сеточных графов и определенные триангуляции покрытых сеткой цилиндрических графов.

Источник

23 Лекция № 22. Планарные графы

Продолжительность: 2 часа (90 мин.)

23.1 Ключевые вопросы

23 Лекция № 22. Планарные графы 1

23.1 Ключевые вопросы 1

23.2 Текст лекции 1

23.2.1 Планарные графы 1

23.2.2 Условия планарности 2

23.2.3 Алгоритм построения плоского изображения графа 3

23.2.4 вопросы для контроля к п. 23.2 5

23.2 Текст лекции

23.2.1 Планарные графы

Планарный граф – это граф, допускающий укладку на плоскости, т.е. он может быть изображен на плоскости так, что никакие ребра не имеют общих точек, кроме своих вершин.

Изображение графа на плоскости с соблюдением этого условия называется плоским графом.

Планарность нужна, например, для реализации печатного монтажа, в процессе разработки которого схема устройства представляется в виде графа: элементы – вершины, связи между выводами элементов – ребра. Печатный монтаж выполняется в одной или нескольких плоскостях, называемых слоями, поэтому обычно возникают вопросы:

Как получить планарное изображение графа?

Если граф не планарен, то приходится удалять (переносить на другой слой, на другую плоскость) отдельные ребра.

Минимальное число ребер, которое надо удалить для получения плоского изображения, называется числом планарности графа и обозначается (G). Для полных графов с

(K_n) = (n–3)(n–4)/2.

Из формулы следует, что при n = 4 (K₄) = 0. Для K₅ (K₅) = 1, следовательно, чтобы граф K₅ стал плоским, из него надо удалить одно ребро.

При перенесении на вторую плоскость, перенесенная часть может опять оказаться не плоской. Тогда отдельные ребра переносят на новую плоскость и т.д.

Минимальное число плоскостей, при котором граф разбивается на плоские части, называется толщиной графа и обозначается t(G).

Толщина произвольного графа удовлетворяет неравенству

t(G).

Здесь [x] – целая часть x.

Толщина полных графов удовлетворяет неравенству

t(K_n).

23.2.2 Условия планарности

Ответ на первый вопрос: – Граф планарен? – можно получить, если воспользоваться условиями планарности.

У связного плоского графа с n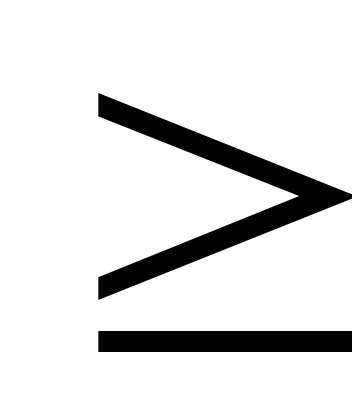3 число ребер m удовлетворяет условию

У связного плоского двудольного графа

Пример. Полный граф K₄ (рис. 23.1, а) – планарен?

В этом графе n = 4, m = 6.

Р исунок 23.1

Подставим эти значения в условие планарности

Условие выполняется. Следовательно, граф планарен. Действительно, граф K₄ можно представить так, как показано на рис. 23.1, б.

Из рисунка ясно, что граф K₄ планарен.

Пример. Полный граф K₅ (рис. 23.1, в) – планарен?

В этом графе n = 5, m = 10.

Подставим эти значения в условие планарности

Условие не выполняется. Следовательно, граф не планарен.

Пример. Двудольный полный граф К_3,3 (рис. 23.1, г) – планарен?

В этом графе n = 6, m = 9.

Подставим эти значения в условие планарности

Условие не выполняется. Следовательно, граф не планарен.

Из примеров видно, что расположить на плоскости без пересечения ребер можно далеко не всякий граф. А вот в трехмерном пространстве так может быть изображен любой конечный граф.

Расположим все вершины на одной прямой рис. 23.2.

Р исунок 23.2

Построим m плоскостей на этой прямой, т. е. для каждого ребра свою плоскость.

Проведем ребра на своих плоскостях. Ребра не пересекаются (кроме как на своих вершинах).

Непланарность графов K₅ и К_3,3 используется для оценки планарности “больших графов”: граф не планарен, если он содержит подграфы вида K₅ или К_3,3, или сводимые к ним.

Грани плоского графа

У плоского графа кроме вершин и ребер можно выделить еще один геометрический образ – грань.

Область плоскости, ограниченная ребрами связного плоского графа и не содержащая внутри себя ни ребер, ни вершин, называется его гранью.

Внешняя неограниченная грань называется бесконечной гранью.

У графа без циклов ровно одна грань – бесконечная. Не следует думать, что она какая–то исключительная. При укладке графа на сферу эта грань ничем не будет отличаться от других.

Число граней f в связном плоском графе определяется из соотношения

где n – число вершин, m – число ребер.

23.2.3 Алгоритм построения плоского изображения графа

Ответ на второй вопрос: – Как получить плоское изображение графа? – дает алгоритм, рассмотренный ниже.

Будем называть куском графа G относительно G₁:

ребро вместе с его концами, которые принадлежат V₁,

Алгоритм использует последовательный процесс присоединения к некоторому плоскому подграфу цепи , оба конца которой (и только они) – вершины . Эта цепь разобьет одну из граней на две.

В качестве начального плоского графа 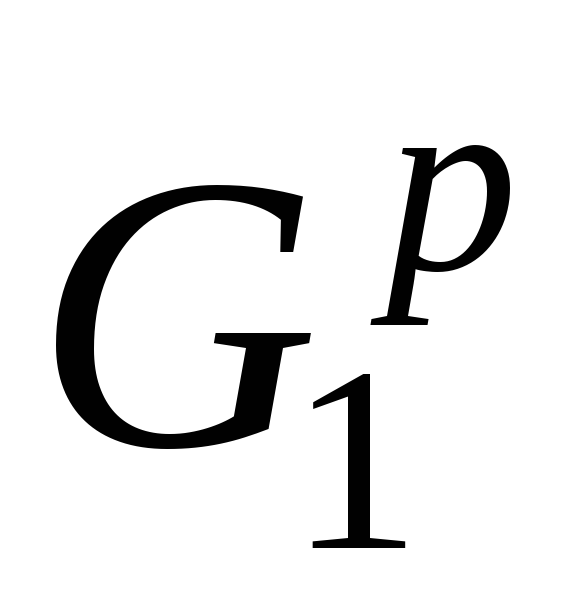выбирают некоторый цикл графа G.

Чтобы перейти от подграфа к , предварительно рассматривают все куски P_j графа G относительно .

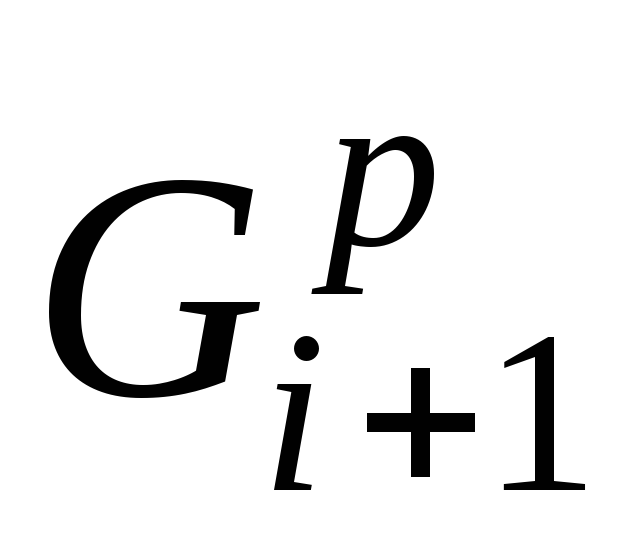
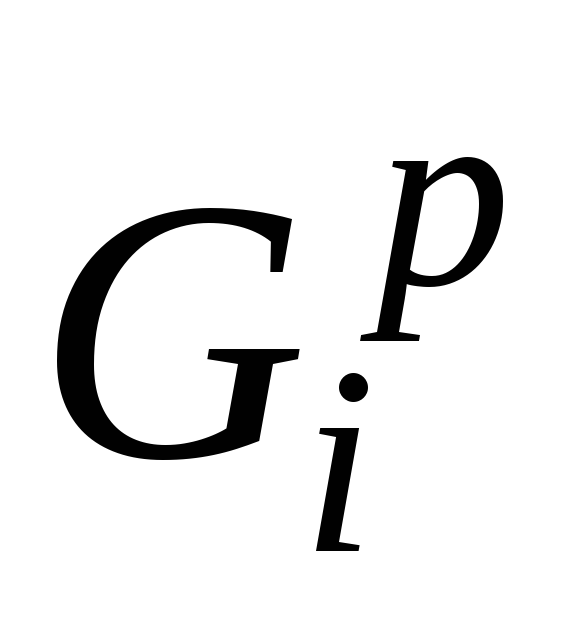
Грань f_k графа и кусок Р_j совместимы, если все его контактные точки принадлежат множеству вершин этой грани.

Для каждого куска определяем грани, которые с ним совместимы. Возможны три случая:

Некоторый кусок не совместим ни с какой гранью графа . Тогда граф не плоский.

Какой–либо кусок совместим с единственной гранью f_k графа . Тогда выберем в этом куске цепь такую, что оба ее конца (и только они) принадлежат . Дополняя ребрами и вершинами этой цепи, получаем , проводя внутри грани f_k.

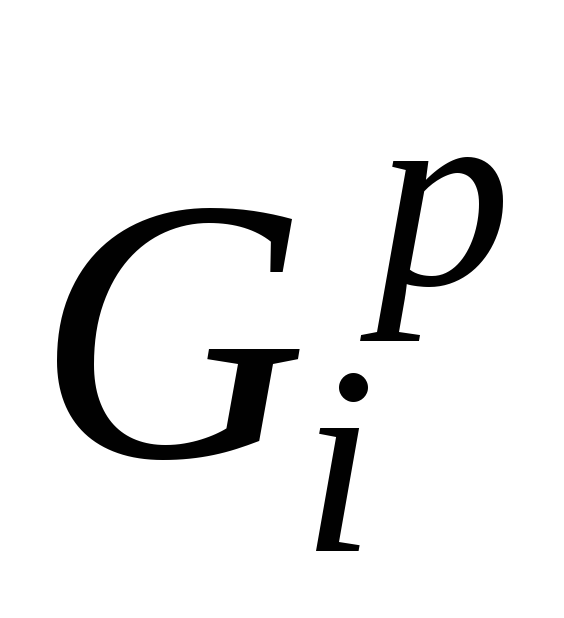
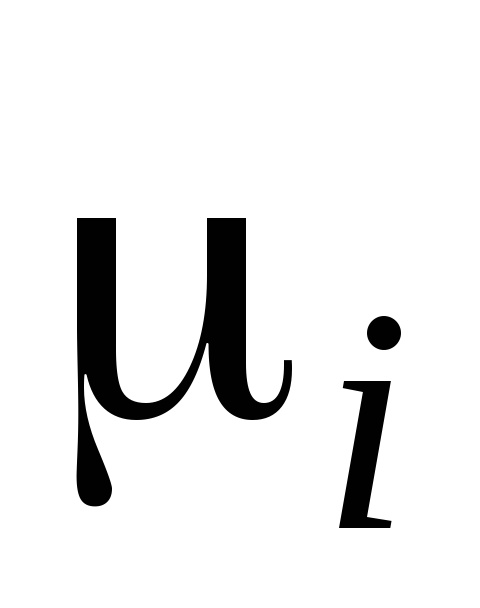
Если каждый из кусков Р_j совместим, по крайней мере, с двумя гранями графа , то можно выбрать цепь в любом из кусков и действовать как в случае 2.

Пример. Проиллюстрируем этот алгоритм на примере графа G(V,E) рис. 23.3.

Р исунок 23.3

Шаг 1. Берем произвольный цикл, например u₀ = (1, 2, 6, 5, 1), представляющий плоский граф (рис. 23.4, а).

Грани:

A₀ — внешняя грань (1, 2, 6, 5, 1),

Куски графа G относительно :

Источник