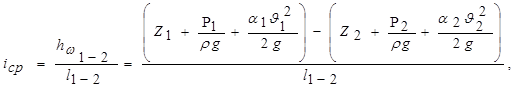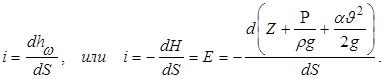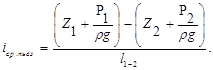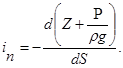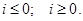что такое пьезометрический уклон

Гидравлический и пьезометрический уклоны

Для характеристики относительного изменения полного напора по длине потока введем понятие о гидравлическом уклоне.

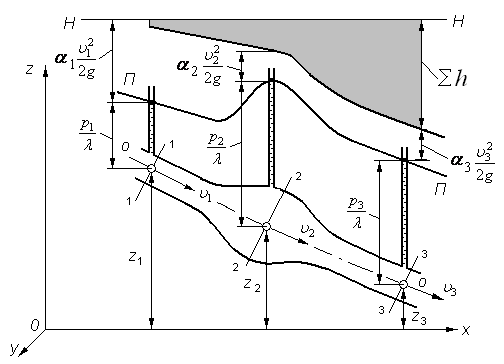
Среднее значение гидравлического уклона на участке потока между сечениями 1–1 и 2–2 (рис.6) определяется как отношение потери напора к длине участка:

где 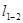− расстояние (по пути движение потока жидкости) между сечениями 1–1 и 2–2.

Гидравлический уклон −величина безразмерная и всегда больше нуля. В общем случае величина гидравлического уклона по длине потока переменная и в данном сечении потока определяется выражением

Здесь знак «минус» указывает на убывание полного напора по пути движения жидкости.

Понятие об уклоне можно ввести и для пьезометрической линии.

Средний пьезометрический уклон определяется по формуле

Значение пьезометрического уклона для некоторого сечения потока определяется выражением

Пьезометрический уклон может быть положительным, равным нулю и отрицательным

В случае, изображенном на рис. 4, пьезометрический уклон отрицательный, а на рис. 6 – положительный.

Источник

Большая Энциклопедия Нефти и Газа

Пьезометрический уклон

Из определения гидравлического уклона следует, что гидравлический уклон мыслим только в вязкой жидкости и всегда направлен в сторону движения жидкости, так как потеря напора по длине неуклонно возрастает. Пьезометрический уклон может быть направлен как в сторону движения, так и в сторону, противоположную-1 движению. [32]

Знак минус здесь показывает, что имеет место действительное понижение напорной линии. Пьезометрическим уклоном называется падение потенциальной энергии на единице длины. [33]

Очевидно, при статическом расчете основания плотины необходимо знать сдвигающую силу, развиваемую потоком. Эта сдвигающая сила зависит от величины пьезометрических уклонов J в разных точках основания. [36]

Пьезометрическая линия при неравномерном плавно изменяющемся движении жидкости ( при распределении давлений в поперечных сечениях по гидростатическому закону) совпадает со свободной поверхностью потока. При неравномерном движении гидравлический уклон /, пьезометрический уклон и уклон дна потока гд в общем случае не равны между собой. [37]

Гидравлический уклон мыслим только в вязкой жидкости. Он всегда направлен в сторону движения, так как потеря энергии по длине неуклонно возрастает. Пьезометрический уклон также связан с потерей энергии. Обычно он направлен в сторону движения. Но в тех случаях, когда живые сечения струйки по течению увеличиваются в результате перехода кинетической энергии в потенциальную, пьезометрические уклоны могут иметь направление, обратное движению. [42]

Источник

Гидравлический и пьезометрический уклоны

Как известно, энергия в природе не может ни теряться, ни возникатьиз ничего. Говоря о потерях энергии в потоке, имеют в виду ту часть механической энергии, которая из-за вязкости жидкости превращается в тепловую и через стенку трубопровода рассеивается в окружающую среду. Для природы в целом эта энергия не потеряна, но для потока она теряется необратимо, поскольку не может быть снова превращена в механическую энергию жидкости.

Причиной всех гидравлических потерь является вязкость жидкости, но далеко не всегда она оказывает существенное влияние на их величину. Потери удельной энергии или гидравлические потери зависят от формы потока, скорости течения и вязкости жидкости, а иногда и от абсолютного давления.

Потери на трение по длине – это потери, обусловленные действием внутреннего трения в жидкости и трением между ограничивающими поток стенками. Эти потери определяются по формуле Дарси-Вейсбаха

, (3.28)

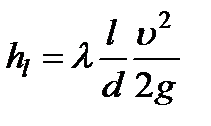
где 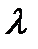— коэффициент трения по длине или коэффициент Дарси.

Местные потери обусловлены местными сопротивлениями, вызывающими деформацию потока. Местные потери напора определяются по формуле Вейсбаха

, (3.29)

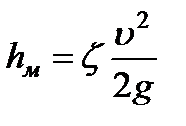
где 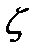— безразмерный коэффициент, так называемый коэффициент местных потерь, или местных гидравлических сопротивлений.

При протекании жидкости через местные сопротивления изменяется её направление и скорость, и возникают завихрения. Примерами местных сопротивлений могут служить сужения, расширения, повороты, дроссели, вентили, клапаны и другие устройства.

В гидравлических расчётах иногда удобно местные потери приводить к потерям по длине, оперируя фиктивной «эквивалентной длиной» трубопровода. Приравняв местные потери к потерям на эквивалентной длине потока, можно легко определить эту длину

,

,

. (3.30)

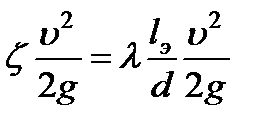
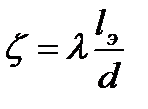
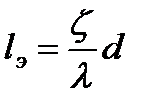
При таком подходе общие гидравлические потери в трубопроводе постоянного диаметра формально определяются как потери подлине

. (3.31)

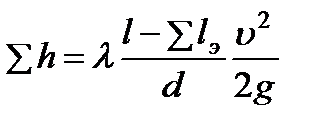
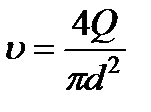
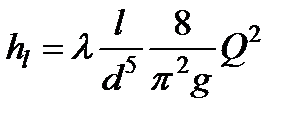
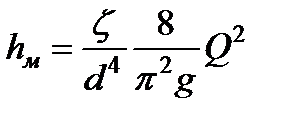
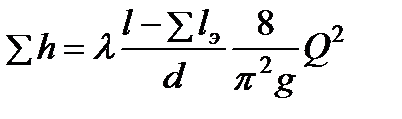
При решении многих задач технической гидродинамики потери удобнее определять через расход. Подставляя в формулы (3.28), (3.29) и (3.31), получим соответственно

; (3.32)

; (3.33)

. (3.34)

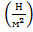
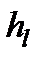
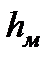
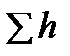
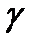
Если потери необходимо выражать в паскалях , то для этого достаточно умножить , или на удельный вес жидкости .

Откладывая последовательно потери и скоростной напор в виде соответствующих вертикальных отрезков вниз от линии полного напора для идеальной жидкости, получим напорную и пьезометрические линии для установившегося потока вязкой несжимаемой жидкости (рис. 3.13).

При построении такой диаграммы (или «эпюры трубопровода») местные потери рассматриваются как сосредоточенные, скачкообразные, поскольку участок возмущения, в пределах которого реализуется каждое из них, обычно мал по сравнению с общей протяжённостью потока. Что касается потерь по длине, то они уменьшают полный напор постепенно на протяжении всего трубопровода, определяя тем самым форму напорной линии.

Рис. 3.13. Линии полных напоров Н-Н и пьезометрических

высот П-П для потока вязкой жидкости

Отношение потерь напора на цилиндрических участках трубопровода к соответствующей длине называют гидравлическим уклоном и обозначают буквой :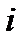

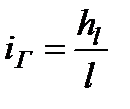
. (3.35)

Гидравлический уклон – величина безразмерная и в общем случае переменная.

Понятие об уклоне можно ввести и для пьезометрической линии. Пьезометрическим уклоном называется изменение удельной потенциальной энергии жидкости, отнесённое к единице длины.

. (3.36)

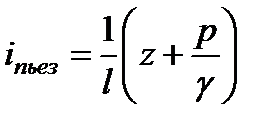
Пьезометрический уклон может быть положительным, равным нулю и отрицательным (рис. 3.13).

На цилиндрических участках трубопровода напорная и пьезометрическая линии представляют собой параллельные прямые, поскольку расстояние между ними по вертикали равно постоянной величине .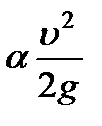

Источник

Уклоны: геометрический, пьезометрический и гидравлический

Геометрическим уклоном называется падение геометрической линии струйки или потока жидкости на единицу длины. Для элементарной струйки, показано на рис. 3.8, на участке длиной l между сечениями 1-1 и 2-2 полное падение геометрической линии S-S равно разности геометрических высот .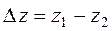

Средний геометрический уклон на

Рис. 3.8 этом участке равен

. (3.41)

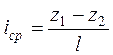
В случае, когда геометрическая линия криволинейна

. (3.42)

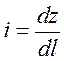
За геометрическую линию напорных потоков (в трубах) обычно принимается их осевая линия.

Пьезометрическим уклоном называется падение пьезометрической линии П-П на единицу длины струйки или потока жидкости.

. (3.43)

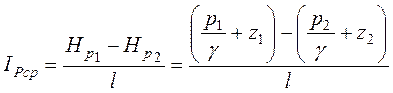
При криволинейной пьезометрической линии

. (3.44)

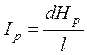
Гидравлическим уклоном называется падение напорной линии Н-Н на единицу длины струйки или потока жидкости

. (3.45)

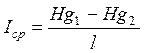
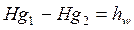
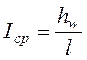
Так как, , то гидравлический уклон выражает так же потерю напора на единицу длины струйки или потока жидкости.

. (3.46)

При криволинейной напорной линии

. (3.47)

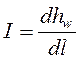
Следует отметить, что геометрический и пьезометрический уклоны в различных случаях могут быть и положительными и отрицательными. Гидравлический уклон всегда положителен.

Дата добавления: 2016-10-07 ; просмотров: 6020 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Тема 21 Уравнение Бернулли для потока конечных размеров. Гидравлический и пьезометрический уклоны

Уравнение Бернулли для установившегося движения невязкой несжимаемой жидкости в форме давлений имеет вид:

r × g × z + р + r × a × 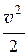= const, (21.1, а)

где r × g × z – гравитационное давление;

р – статическое давление;

r × 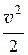– динамическое давление.

Для двух произвольных сечений 1-1 и 2-2 уравнение имеет вид:

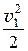
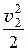
r × g × z₁ + р₁ + r × a₁ × = r × g × z₂ + р₂ + r × a₂ × = const. (21.1, б)

Уравнение Бернулли для установившегося движения невязкой несжимаемой жидкости в форме напоров имеет вид:

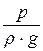
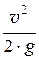
z + + a× = Н = const, (21.2, а)

где z – удельная потенциальная энергия положения;

– удельная потенциальная энергия давления;

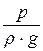
a × 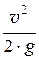– удельная кинетическая энергия (динамический напор для потока);

Н – полная удельная энергия потока.

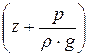
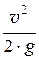
Таким образом, полная удельная энергия потока есть сумма удельной потенциальной энергии и удельной кинетической энергии a × .

Для двух произвольных сечений 1-1 и 2-2 уравнение имеет вид:

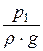
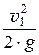
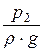
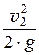
z₁ + + a₁ × = z₂ + + a₂ × = Н = const. (21.2, б)

С энергетической точки зрения уравнение Бернулли можно сформулировать так:

при установившемся движении невязкой несжимаемой жидкости вдоль потока сумма удельных энергий – потенциальной (положения и давления) и кинетической – есть величина постоянная.

Все члены уравнения Бернулли имеют линейную размерность и их можно интерпретировать как высоты:

z – геометрическая высота, то есть высота положения рассматриваемой точки пространства с жидкостью (центра тяжести сечения) над горизонтальной плоскостью сравнения x0y;

Если в уравнении Бернулли:

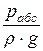
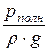
· р – абсолютное (полное) давление, то величина = – высота давления;

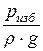
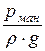
· р – избыточное (манометрическое) давление, то величина = называется пьезометрической высотой;

a × 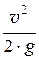– скоростн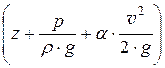ая (или динамическая) высота.

Н = – полная высота в данном сечении потока.

Таким образом, геометрический смысл уравнения Бернулли можно сформулировать так:

при установившемся движении невязкой несжимаемой жидкости вдоль потока сумма высот – положения, давления (или пьезометрической) и скоростной – есть величина постоянная.

В потоке скорости в разных точках поперечного сечения различны, а скоростной напор, определяемый средней скоростью v, дополнен коэффициентом кинетической энергии (или коэффициентом Кориолиса) a. Величина этого коэффициента отражает степень неравномерности распределения скоростей по сечению потока. Коэффициент равен отношению истинной кинетической энергии массы жидкости, протекающей через живое сечение, к кинетической энергии, вычисленной в предположении, что во всех точках живого сечения местные скорости равны средней скорости.

Обычно при прямолинейном турбулентном движении в трубах a = 1,03…1,1. Обычно при расчётах при турбулентном течении в трубах принимают коэффициент Кориолиса a равным 1,1 или 1. При прямолинейном ламинарном движении в трубах a = 2.

При движении реальной (вязкой) жидкости часть механической энергии теряется (переходит в тепловую).

Уравнение Бернулли для установившегося движения вязкой несжимаемой жидкости между двумя сечениями имеет вид:

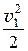
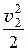
r × g × z₁ + р₁ + r × a₁ × = r × g × z₂ + р₂ + r × a₂× + Dр, (21.3)

где Dр – потери давления на участке между рассматриваемыми сечениями;

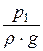
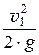
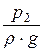
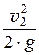
z₁ + + a₁× = z₂ + + a₂ × + Dh_пот, (21.4)

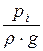
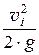
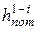
z_i + + a_i × + D = Н = const.

где Dh_пот – потери напора на участке между рассматриваемыми сечениями.

Для потока жидкости сумма удельной потенциальной и удельной кинетической энергии

Н = 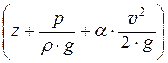(21.5)

называется гидродинамическим (или полным) напором.

При движении вязкой жидкости линия удельной энергии (напорная линия) не горизонтальна, как при движении невязкой жидкости, а представляет собой наклонную линию, так как удельная энергия потока (гидродинамический напор) Е = Н = 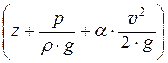при движении вязкой жидкости уменьшается в направлении движения.

Энергетический смысл уравнения Бернулли для потока вязкой жидкости:

удельная энергия потока в предыдущем сечении всегда больше чем в последующем на величину потерь удельной энергии.

Геометрический смысл уравнения Бернулли для потока вязкой жидкости:

полная высота в предыдущем сечении всегда больше чем в последующем на высоту потерь Dh_пот.

Гидравлическим уклоном i называется отношение потерь напора Dh_потк длине участка l, на котором эти потери происходят:

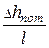
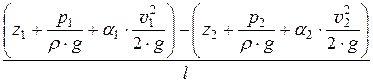
i = = > 0. (21.6, а)

Так как напор уменьшается вдоль движения, то гидравлический уклон всегда положителен.

Удельная потенциальная энергия 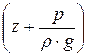(пьезометрический напор) в направлении движения может, и уменьшатся, и увеличиваться, в зависимости от конкретных условий.

Пьезометрическим уклоном i_п называется отнесённое к единице длины изменение пьезометрического напора 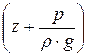или изменение отметок пьезометрической линии.

Для двух сечений имеем

i_п = 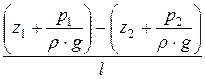. (21.7, б)

Пьезометрический уклон может быть положительным, отрицательным и равным нулю. Пьезометрический уклон считается положительным, если по течению пьезометрическая линия понижается.

Источник