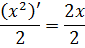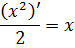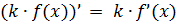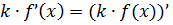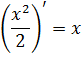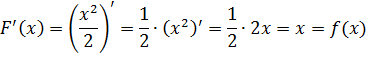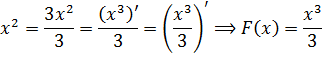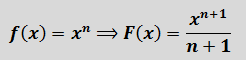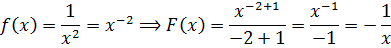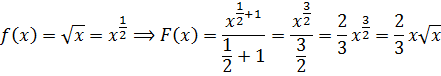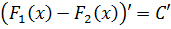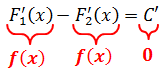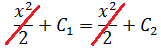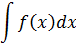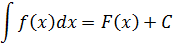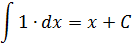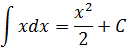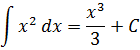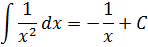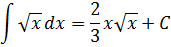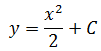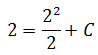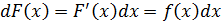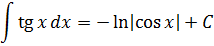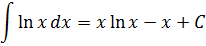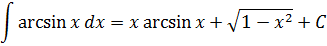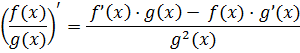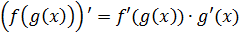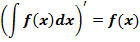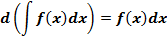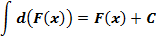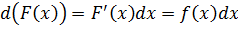что такое первообразная в математике

Первообразная функция и неопределенный интеграл

Первообразная

Определение первообразной функции

Можно прочесть двумя способами:

Правила вычисления первообразных

Запомни!

Любая функция F(x) = х 2 + С, где С — произвольная постоянная, и только такая функция, является первообразной для функции f(x) = 2х.

Связь между графиками функции и ее первообразной:

Неопределенный интеграл

Определение:

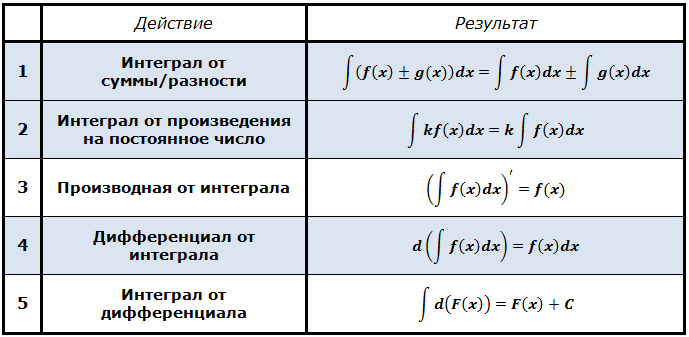
Свойства неопределённого интеграла

Таблица первообразных и неопределенных интегралов

Функция

Первообразная

F(x) + C

Неопределенные интегралы

\int f(x) dx = F(x) + C

Формула Ньютона–Лейбница

Пусть f (х) данная функция, F её произвольная первообразная.

То есть, интеграл функции f (x) на интервале [a;b] равен разности первообразных в точках b и a.

Площадь криволинейной трапеции

Криволинейной трапецией называется фигура, ограниченная графиком неотрицательной и непрерывной на отрезке [a;b] функции f, осью Ox и прямыми x = a и x = b.

Площадь криволинейной трапеции находят по формуле Ньютона-Лейбница:

Источник

Что такое первообразная в математике

Изучая математику, мы не раз сталкивались со взаимно-обратными операциями.
Примерами взаимно-обратных операций являются:

Операция, обратная дифференцированию, называется интегрированием, а процессом, обратным нахождению производной, является процесс нахождения первообразной.

Или Первообразной для функции F(x) называется функция, производная которой равна данной.

Зад ача интегрирования состоит в том, чтобы для заданной функции найти все ее первообразные. Важную роль в решении этой задачи играет признак постоянства функции:
Если

Все первообразные функции а можно записать с помощью одной формулы, которую называют общим видом первообразных для функции f.

Основное свойство первообразных:
Любая первообразная для функции f на промежутке I может быть записана в виде

где F(x) – одна из первообразных для функции f(х) на промежутке I, а С – произвольная постоянная.

В этом утверждении сформулированы два свойства первообразной
1) какое бы число ни подставить вместо С, получим первообразную для f на промежутке I;
2) какую бы первообразную Ф для f на промежутке I ни взять, можно подобрать такое число С, что для всех х из промежутка I будет выполнено равенство Ф(х) = F(x) + C.

Геометрический смысл первообразной

Пример 1. Выяснить, является ли функция F (x) = х 3 – 3х + 1 первообразной для функции f(x) = 3(х 2 – 1).

Решение: F'(x) = (х 3 – 3х + 1)′ = 3х 2 – 3 = 3(х 2 – 1) = f(x), т.е. F'(x) = f(x), следовательно, F(x) является первообразной для функции f(x).

Пример 2. Найти все первообразные функции f(x): f(x) = х 4 + 3х 2 + 5

Решение: Используя таблицу и правила нахождения первообразных, получим:

Ответ:

Задание № 1
Скачай задание из Приложений к странице. Распечатай, выполни предложенные задания, отсканируй и отошли учителю

Источник

Первообразная и неопределенный интеграл, их свойства

Определение первообразной

Определение неопределенного интеграла

Имея заданный дифференциал функции, мы можем найти неизвестную функцию.

∫ f ( x ) d x ‘ = F ( x ) + C ‘ = f ( x )

∫ d ( F ( x ) ) = ∫ F ‘ ( x ) d x = ∫ f ( x ) d x = F ( x ) + C

∫ f ( x ) ± g ( x ) ) d x = ∫ f ( x ) d x ± ∫ g ( x ) d x

Промежуточные равенства первого и второго свойств неопределенного интеграла мы привели в качестве пояснения.

Для того, чтобы доказать третье и четвертое свойства, необходимо найти производные от правых частей равенств:

k · ∫ f ( x ) d x ‘ = k · ∫ d ( x ) d x ‘ = k · f ( x ) ∫ f ( x ) d x ± ∫ g ( x ) d x ‘ = ∫ f ( x ) d x ‘ ± ∫ g ( x ) d x ‘ = f ( x ) ± g ( x )

Производные правых частей равенств равны подынтегральным функциям, что является доказательством первого свойства. Его же мы используем в последних переходах.

Как видите, задача интегрирования представляет собой обратный процесс по отношению к задаче дифференцирования. Обе эти задачи тесно связаны между собой.

Первое свойство может быть использовано для проведения проверки интегрирования. Для проверки нам достаточно вычислить производную полученного результата. Если полученная функция будет равна подынтегральной функции, то интегрирование проведено верно.

Благодаря второму свойству по известному дифференциалу функции мы можем найти ее первообразную и использовать ее для вычисления неопределенного интеграла.

Решение

Используя таблицу производных основных элементарных функций получаем

d ( ln x ) = ( ln x ) ‘ d x = d x x = f ( x ) d x ∫ f ( x ) d x = ∫ d x x = ∫ d ( ln ( x ) )

Ответ: f ( x ) = 1 x = ln ( x ) + 1

Необходимо найти неопределенный интеграл ∫ 2 sin x 2 cos x 2 d x и проверить результат вычисления дифференцированием.

Решение

Используем таблицу производных для тригонометрических функций, получим:

Проверим полученный результат дифференцированием.

В результате проверки мы получили подынтегральную функцию. Это значит, что интегрирование было проведено нами верно. Для осуществления последнего перехода мы использовали формулу синуса двойного угла.

Если таблицу производных основных элементарных функций переписать в виде дифференциалов, то из нее по второму свойству неопределенного интеграла можно составить таблицу первообразных.

Подробнее эту тему мы рассмотрим в следующем разделе «Таблица первообразных (таблица неопределенных интегралов)».

Источник

Первообразная функции и общий вид

Этот урок — первый из серии видео, посвященных интегрированию. В нём мы разберём, что такое первообразная функции, а также изучим элементарные приёмы вычисления этих самых первообразных.

На самом деле здесь нет ничего сложного: по существу всё сводится к понятию производной, с которым вы уже должны знакомы.:)

Сразу отмечу, что, поскольку это самый первый урок в нашей новой теме, сегодня не будет никаких сложных вычислений и формул, но то, что мы изучим сегодня, ляжет в основу гораздо более сложных выкладок и конструкций при вычислении сложных интегралов и площадей.

Кроме того, приступая к изучению интегрирования и интегралов в частности, мы неявно предполагаем, что ученик уже, как минимум, знаком к понятиям производной и имеет хотя бы элементарные навыки их вычисления. Без четкого понимания этого, делать в интегрировании совершенно нечего.

Однако здесь же кроется одна из самых частых и коварных проблем. Дело в том, что, начиная вычислять свои первые первообразные, многие ученики путают их с производными. В результате на экзаменах и самостоятельных работах допускаются глупые и обидные ошибки.

Поэтому сейчас я не буду давать четкого определения первообразной. А взамен предлагаю вам посмотреть, как она считается на простом конкретном примере.

Что такое первообразная и как она считается

Допустим, нам необходимо посчитать следующую производную:

Мы знаем такую формулу:

Считается эта производная элементарно:

Но мы можем записать и так, согласно определению производной:

А теперь внимание: то, что мы только что записали и есть определением первообразной. Но, чтобы записать ее правильно, нужно написать следующее:

Аналогично запишем и такое выражение:

Если мы обобщим это правило, то сможем вывести такую формулу:

Теперь мы можем сформулировать четкое определение.

Первообразной функции называется такая функция, производная которой равна исходной функции.

Вопросы о первообразной функции

Казалось бы, довольно простое и понятное определение. Однако, услышав его, у внимательного ученика сразу возникнет несколько вопросов:

На последний вопрос я отвечу сразу. К сожалению, первообразная, в отличие от производной, считается не всегда. Нет такой универсальной формулы, по которой из любой исходной конструкции мы получим функцию, которая будет равна этой сходной конструкции. А что касается степеней и констант — сейчас мы об этом поговорим.

Решение задач со степенными функциями

Давайте попробуем посчитать такое выражение:

Поэтому мы с уверенностью можем записать следующее:

Эту формулу нужно знать, точно так же, как и производную степенной функции.

Итак, что нам известно на данный момент:

Идем далее. Что нам еще может потребоваться? Конечно же, правило вычисления первообразных от суммы и от разности. Запишем так:

\[f\left( x \right)\to F\left( x \right)\]

\[g\left( x \right)\to G\left( x \right)\]

\[c\cdot f\to c\cdot F\left( c=const \right)\]

А если простейшие функции мы начнем умножать и делить, как тогда посчитать первообразную произведения или частного. К сожалению, аналогии с производной произведения или частного здесь не работают. Какой-либо стандартной формулы не существует. Для некоторых случаев существуют хитрые специальные формулы — с ними мы познакомимся на будущих видеоуроках.

Однако запомните: общей формулы, аналогичной формуле для вычисления производной частного и произведения, не существует.

Решение реальных задач

Задача № 1

Давайте каждую из степенных функций посчитаем отдельно:

Возвращаясь к нашему выражению, мы запишем общую конструкцию:

Задача № 2

Как я уже говорил, первообразные произведений и частного «напролом» не считаются. Однако здесь можно поступить следующим образом:

Мы разбили дробь на сумму двух дробей.

\[F\left( x \right)=1\cdot x+\ln x\]

\[F\left( x \right)=x+\ln x\]

Все эти приемы можно и нужно комбинировать. Степенные выражения можно

Решение выражений со степенью с рациональным показателем

Пример № 1

Посчитаем каждый корень отдельно:

Итого всю нашу конструкцию можно записать следующим образом:

Пример № 2

Следовательно, мы получим:

Итого, собирая все в одно выражение, можно записать:

Пример № 3

Надеюсь, я никого не удивлю, если скажу, что то, что мы только что изучали — это лишь самые простые вычисления первообразных, самые элементарные конструкции. Давайте сейчас рассмотрим чуть более сложные примеры, в которых помимо табличных первообразных еще потребуется вспомнить школьную программу, а именно, формулы сокращенного умножения.

Решение более сложных примеров

Задача № 1

Вспомним формулу квадрата разности:

Давайте перепишем нашу функцию:

\[f\left( x \right)=\left( \sqrt[3] \right)-2\cdot \sqrt[3]\cdot 2+4\]

Первообразную такой функции нам сейчас предстоит найти:

Собираем все в общую конструкцию:

Задача № 2

В этом случае нам нужно раскрыть куб разности. Вспомним:

С учетом этого факта можно записать так:

Давайте немного преобразуем нашу функцию:

Считаем как всегда — по каждому слагаемому отдельно:

Запишем полученную конструкцию:

Задача № 3

Сверху у нас стоит квадрат суммы, давайте его раскроем:

Давайте напишем итоговое решение:

А теперь внимание! Очень важная вещь, с которой связана львиная доля ошибок и недопониманий. Дело в том, что до сих пор считая первообразные с помощью производных, приводя преобразования, мы не задумывались о том, чему равна производная константы. А ведь производная константы равна «нулю». А это означает, что можно записать такие варианты:

Вот это очень важно понимать: если производная функции всегда одна и та же, то первообразных у одной и той же функции бесконечно много. Просто к нашим первообразным мы можем дописывать любые числа-константы и получать новые.

Еще раз переписываем наши конструкции:

Во второй нашей функции мы получим следующую конструкцию:

И вот теперь мы действительно получили то, что от нас требовалось в исходном условии задачи.

Решение задач на нахождение первообразных с заданной точкой

Сейчас, когда мы знаем о константах и об особенностях записи первообразных, вполне логично возникает следующий тип задач, когда из множества всех первообразных требуется найти одну-единственную такую, которая проходила бы через заданную точку. В чем состоит эта задача?

Дело в том, что все первообразные данной функции отличаются лишь тем, что они сдвинуты по вертикали на какое-то число. А это значит, что какую бы точку на координатной плоскости мы не взяли, обязательно пройдет одна первообразная, и, причем, только одна.

Итак, задачи, которые сейчас мы будем решать, сформулированы следующем образом: не просто найти первообразную, зная формулу исходной функции, а выбрать именно такую из них, которая проходит через заданную точку, координаты которой будут даны в условии задачи.

Пример № 1

Для начала просто посчитаем каждое слагаемое:

Теперь подставляем эти выражения в нашу конструкцию:

Давайте запишем то самое решение, которое мы искали:

Пример № 2

В первую очередь необходимо раскрыть квадрат разности по формуле сокращенного умножения:

Исходная конструкция запишется следующим образом:

Осталось отобразить итоговое выражение:

Решение тригонометрических задач

Забегая наперед, хотел бы отметить, что тот прием, который мы сейчас будем использовать для нахождения первообразных от тригонометрических функций, на самом деле, является универсальным приемом для самопроверки.

Задача № 1

Вспомним следующую формулу:

Исходя из этого, мы можем записать:

Перепишем выражение с учетом этого факта:

Задача № 2

Тут будет чуть сложнее. Сейчас увидите, почему.

Вспомним такую формулу:

Чтобы избавится от «минуса», необходимо сделать следующее:

Вот наша конструкция

Итого запишем окончательную конструкцию:

Вот и все, о чем я хотел сегодня вам рассказать. Мы изучили сам термин первообразных, как считать их от элементарных функций, а также как находить первообразную, проходящую через конкретную точку на координатной плоскости.

Надеюсь, этот урок хоть немного поможет вам разобраться в этой сложной теме. В любом случае, именно на первообразных строятся неопределенные и неопределенные интегралы, поэтому считать их совершенно необходимо. На этом у меня все. До новых встреч!

Источник

Что такое первообразная? Понятие первообразной.

Прежде чем знакомиться с понятием первообразной, давайте в самых общих чертах вспомним самую обычную производную. Не углубляясь в занудную теорию пределов, приращений аргумента и прочего, можно сказать, что нахождение производной (или дифференцирование) — это просто математическая операция над функцией. И всё. Берётся любая функция (допустим, f(x) = x 2 ) и по определённым правилам преобразовывается, превращаясь в новую функцию. И вот эта самая новая функция и называется производной.

Грубо говоря, f(x) = x 2 — это мама, а f’(x) = 2x — её любимая дочка.) Это понятно. Идём дальше.

Математики — народ неугомонный. На каждое своё действие стремятся найти противодействие. 🙂 Есть сложение — есть и вычитание. Есть умножение — есть и деление. Возведение в степень — извлечение корня. Синус — арксинус. Точно также есть дифференцирование – значит, есть и… интегрирование.)

А теперь поставим такую интересную задачу. Есть у нас, допустим, такая простенькая функция f(x) = 1. И нам надо ответить на такой вопрос:

Производная КАКОЙ функции даёт нам функцию f(x) = 1?

Иными словами, видя дочку, с помощью анализа ДНК, вычислить, кто же её мамаша. 🙂 Так от какой же исходной функции (назовём её F(x)) произошла наша производная функция f(x) = 1? Или, в математической форме, для какой функции F(x) выполняется равенство:

Пример элементарный. Я старался.) Просто подбираем функцию F(x) так, чтобы равенство сработало. 🙂 Ну как, подобрали? Да, конечно! F(x) = x. Потому, что:

Разумеется, найденную мамочку F(x) = x надо как-то назвать, да.) Знакомьтесь!

Первообразной для функции f(x) называется такая функция F(x), производная которой равна f(x), т.е. для которой справедливо равенство F’(x) = f(x).

Вот и всё. Больше никаких научных хитростей. В строгом определении добавляется ещё дополнительная фраза «на промежутке Х». Но мы пока в эти тонкости углубляться не будем, ибо наша первоочередная задача — научиться находить эти самые первообразные.

В нашем случае как раз и получается, что функция F(x) = x является первообразной для функции f(x) = 1.

Почему? Потому что F’(x) = f(x) = 1. Производная икса есть единица. Возражений нет.)

Термин «первообразная» по-обывательски означает «родоначальница», «родитель», «предок». Сразу же вспоминаем самого родного и близкого человека.) А сам поиск первообразной — это восстановление исходной функции по известной её производной. Иными словами, это действие, обратное дифференцированию. И всё! Сам же этот увлекательный процесс тоже называется вполне научно — интегрирование. Но об интегралах — позже. Терпение, друзья!)

Запоминаем:

Интегрирование — это математическая операция над функцией (как и дифференцирование).

Интегрирование — операция, обратная дифференцированию.

Первообразная — результат интегрирования.

А теперь усложним задачу. Найдём теперь первообразную для функции f(x) = x. То есть, найдём такую функцию F(x), чтобы её производная равнялась бы иксу:

Кто дружит с производными, тому, возможно, на ум придёт что-то типа:

Что ж, респект и уважуха тем, кто помнит таблицу производных!) Верно. Но есть одна проблемка. Наша исходная функция f(x) = x, а (x 2 )’ = 2x. Два икс. А у нас после дифференцирования должен получиться просто икс. Не катит. Но…

Мы с вами народ учёный. Аттестаты получили.) И со школы знаем, что обе части любого равенства можно умножать и делить на одно и то же число (кроме нуля, разумеется)! Так уж тождественные преобразования устроены. Вот и реализуем эту возможность себе во благо.)

Мы ведь хотим, чтобы справа остался чистый икс, верно? А двойка мешает… Вот и берём соотношение для производной (x 2 )’ = 2x и делим обе его части на эту самую двойку:

Так, уже кое-чего проясняется. Идём дальше. Мы знаем, что любую константу можно вынести за знак производной. Вот так:

Все формулы в математике работают как слева направо, так и наоборот — справа налево. Это значит, что, с тем же успехом, любую константу можно и внести под знак производной:

В нашем случае спрячем двойку в знаменателе (или, что то же самое, коэффициент 1/2) под знак производной:

А теперь внимательно присмотримся к нашей записи. Что мы видим? Мы видим равенство, гласящее, что производная от чего-то (это что-то — в скобочках) равняется иксу.

Полученное равенство как раз и означает, что искомой первообразной для функции f(x) = x служит функция F(x) = x 2 /2. Та, что стоит в скобочках под штрихом. Прямо по смыслу первообразной.) Что ж, проверим результат. Найдём производную:

Отлично! Получена исходная функция f(x) = x. От чего плясали, к тому и вернулись. Это значит, что наша первообразная найдена верно.)

Полученная формулка, между прочим, справедлива не только для натурального показателя степени n, но и для любого другого — отрицательного, дробного. Это позволяет легко находить первообразные от простеньких дробей и корней.

Что такое неопределённый интеграл? Таблица интегралов.

Идём дальше. Те студенты, которые хотя бы мало-мальски «шарят» в производных, — люди грамотные. И, возможно, уже приготовили мне убойный вопрос. 🙂

Скажем, чему равна производная для функции F(x) = x? Ну, единица, единица — слышу недовольные ответы… Всё верно. Единица. Но… Для функции G(x) = x+1 производная тоже будет равна единице:

Также производная будет равна единице и для функции x+1234, и для функции x-10, и для любой другой функции вида x+C, где С — любая константа. Ибо производная любой константы равна нулю, а от прибавления/вычитания нуля никому ни холодно ни жарко.)

Получается неоднозначность. Выходит, что для функции f(x) = 1 первообразной служит не только функция F(x) = x, но и функция F₁(x) = x+1234 и функция F₂(x) = x-10 и так далее!

Но! Всех наших родственников-первообразных объединяет одно важное свойство. На то они и родственники.) Свойство настолько важное, что в процессе разбора приёмов интегрирования мы про него ещё не раз вспомним. И будем вспоминать ещё долго.)

Вот оно, это свойство:

Любые две первообразные F₁(x) и F₂(x) от одной и той же функции f(x) отличаются на константу:

Кому интересно доказательство — штудируйте литературу или конспекты лекций.) Ладно, так уж и быть, докажу. Благо доказательство тут элементарное, в одно действие. Берём равенство

и дифференцируем обе его части. То есть, просто тупо ставим штрихи:

Вот и всё. Как говорится, ЧТД. 🙂

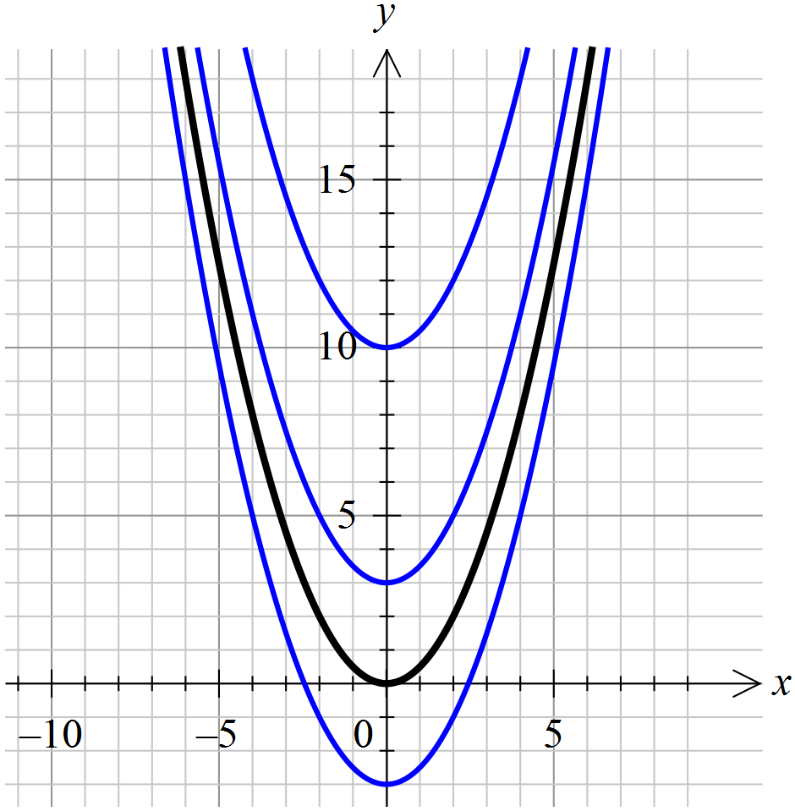
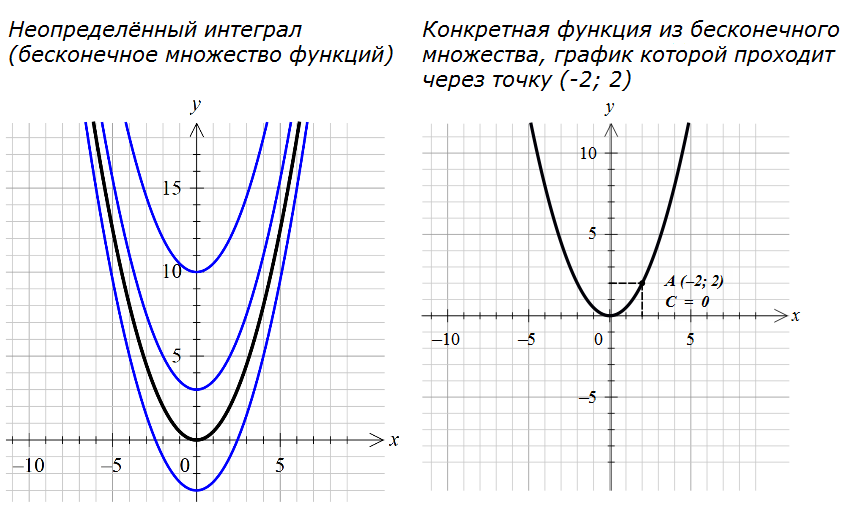
Посмотрим, как это выглядит на примере функции f(x) = x. Все её первообразные, как нам уже известно, имеют общий вид F(x) = x 2 /2+C. На картинке это выглядит как бесконечное множество парабол, получаемых из «основной» параболы y = x 2 /2 сдвигом вдоль оси OY вверх или вниз в зависимости от значения константы С.

Помните школьное построение графика функции y=f(x)+a сдвигом графика y=f(x) на «а» единиц вдоль оси игреков?) Вот и тут то же самое.)

Причём, обратите внимание: наши параболы нигде не пересекаются! Оно и естественно. Ведь две различные функции y₁(x) и y₂(x) неизбежно будут соответствовать двум различным значениям константы — С₁ и С₂.

Поэтому уравнение y₁(x) = y₂(x) никогда не имеет решений:

А теперь мы плавненько подходим ко второму краеугольному понятию интегрального исчисления. Как мы только что установили, у всякой функции f(x) существует бесконечное множество первообразных F(x) + C, отличающихся друг от друга на константу. Это самое бесконечное множество тоже имеет своё специальное название.) Что ж, прошу любить и жаловать!

Что такое неопределённый интеграл?

Множество всех первообразных для функции f(x) называется неопределённым интегралом от функции f(x).

Вот и всё определение.)

«Интеграл» — с подробной расшифровкой этого зверского слова мы познакомимся в следующем большом разделе, посвящённом определённым интегралам. А пока, в грубой форме, будем считать интегралом нечто общее, единое, целое. А интегрированием — объединение, обобщение, в данном случае переход от частного (производной) к общему (первообразным). Вот, как-то так.

Обозначается неопределённый интеграл вот так:

Читается так же, как и пишется: интеграл эф от икс дэ икс. Или интеграл от эф от икс дэ икс. Ну, вы поняли.)

Теперь разберёмся с обозначениями.

∫ — значок интеграла. Смысл тот же, что и штрих для производной.)

d — значок дифференциала. Не пугаемся! Зачем он там нужен — чуть ниже.

f(x) — подынтегральная функция (через «ы»).

f(x)dx — подынтегральное выражение. Или, грубо говоря, «начинка» интеграла.

Согласно смыслу неопределённого интеграла,

Здесь F(x) — та самая первообразная для функции f(x), которую мы так или иначе нашли сами. Как именно нашли — не суть. Например, мы установили, что F(x) = x 2 /2 для f(x)=x.

А теперь вернёмся к нашим самым первым примерам на поиск первообразной. В терминах неопределённого интеграла можно теперь смело записать:

И так далее.) Идея понятна, думаю. Ни в коем случае не забываем приплюсовывать константу С!

Что такое интегральная константа и зачем она нужна?

Вопрос очень интересный. И очень (ОЧЕНЬ!) важный. Интегральная константа из всего бесконечного множества первообразных выделяет ту линию, которая проходит через заданную точку.

В чём суть. Из исходного бесконечного множества первообразных (т.е. неопределённого интеграла) надо выделить ту кривую, которая будет проходить через заданную точку. С какими-то конкретными координатами. Такое задание всегда и везде встречается при начальном знакомстве с интегралами. Как в школе, так и в ВУЗЕ.

Среди множества всех первообразных функции f=x выделить ту, которая проходит через точку (2;2).

Начинаем думать головой… Множество всех первоообразных — это значит, сначала надо проинтегрировать нашу исходную функцию. То есть, икс (х). Этим мы занимались чуть выше и получили такой ответ:

А теперь разбираемся, что именно мы получили. Мы получили не одну функцию, а целое семейство функций. Каких именно? Вида y=x 2 /2+C. Зависящее от значения константы С. И вот это значение константы нам и предстоит теперь «отловить».) Ну что, займёмся ловлей?)

Удочка наша — семейство кривых (парабол) y=x 2 /2+C.

Константы — это рыбины. Много-много. Но на каждую найдётся свой крючок и приманка.)

А что же служит приманкой? Правильно! Наша точка (-2;2).

Вот и подставляем координаты нашей точки в общий вид первообразных! Получим:

Отсюда уже легко ищется C = 0.

Что сиё означает? Это значит, что из всего бесконечного множества парабол вида y=x 2 /2+C только парабола с константой С=0 нам подходит! А именно: y=x 2 /2. И только она. Только эта парабола будет проходить через нужную нам точку (-2; 2). А в се остальные параболы из нашего семейства проходить через эту точку уже не будут. Через какие-то другие точки плоскости — да, а вот через точку (2; 2) — уже нет. Уловили?

Для наглядности вот вам две картинки — всё семейство парабол (т.е. неопределённый интеграл) и какая-то конкретная парабола, соответствующая конкретному значению константы и проходящая через конкретную точку:

Видите, насколько важно учитывать константу С при интегрировании! Так что не пренебрегаем этой буковкой «С» и не забываем приписывать к окончательному ответу.

А теперь разберёмся, зачем же внутри интегралов везде тусуется символ dx. Забывают про него студенты частенько… А это, между прочим, тоже ошибка! И довольно грубая. Всё дело в том, что интегрирование — операция, обратная дифференцированию. А что именно является результатом дифференцирования? Производная? Верно, но не совсем. Дифференциал!

В нашем случае, для функции f(x) дифференциал её первообразной F(x), будет:

Кому непонятна данная цепочка — срочно повторить определение и смысл дифференциала и то, как именно он раскрывается! Иначе в интегралах будете тормозить нещадно….

Поэтому, строго говоря, интеграл «берётся» не от функции f(x), как принято считать, а от дифференциала f(x)dx! Но, в упрощённом варианте, принято говорить, что «интеграл берётся от функции». Или: «Интегрируется функция f(x)«. Это одно и то же. И мы будем говорить точно так же. Но про значок dx при этом забывать не будем! 🙂

И сейчас я подскажу, как его не забыть при записи. Представьте себе сначала, что вы вычисляете обычную производную по переменной икс. Как вы обычно её пишете?

Вот так: f’(x), y’(x), у’_x. Или более солидно, через отношение дифференциалов: dy/dx. Все эти записи нам показывают, что производная берётся именно по иксу. А не по «игреку», «тэ» или какой-то там другой переменной.)

Так же и в интегралах. Запись ∫ f(x)dx нам тоже как бы показывает, что интегрирование проводится именно по переменной икс. Конечно, это всё очень упрощённо и грубо, но зато понятно, я надеюсь. И шансы забыть приписать вездесущее dx резко снижаются.)

Итак, что такое же неопределённый интеграл — разобрались. Прекрасно.) Теперь хорошо бы научиться эти самые неопределённые интегралы вычислять. Или, попросту говоря, «брать». 🙂 И вот тут студентов поджидает две новости — хорошая и не очень. Пока начнём с хорошей.)

Новость хорошая. Для интегралов, так же как и для производных, существует своя табличка. И все интегралы, которые нам будут встречаться по пути, даже самые страшные и навороченные, мы по определённым правилам будем так или иначе сводить к этим самым табличным.)

Итак, вот она, таблица интегралов!

Вот такая вот красивая табличка интегралов от самых-самых популярных функций. Рекомендую обратить отдельное внимание на группу формул 1-2 (константа и степенная функция). Это — самые употребительные формулы в интегралах!

Третья группа формул (тригонометрия), как можно догадаться, получена простым обращением соответствующих формул для производных.

C четвёртой группой формул (показательная функция) — всё аналогично.

А вот четыре последние группы формул (5-8) для нас новые. Откуда же они взялись и за какие такие заслуги именно эти экзотические функции, вдруг, вошли в таблицу основных интегралов? Чем же эти группы функций так выделяются на фоне остальных функций?

Так уж сложилось исторически в процессе развития методов интегрирования. Когда мы будем тренироваться брать самые-самые разнообразные интегралы, то вы поймёте, что интегралы от перечисленных в таблице функций встречаются очень и очень часто. Настолько часто, что математики отнесли их к табличным.) Через них выражаются очень многие другие интегралы, от более сложных конструкций.

Ради интереса можно взять какую-нибудь из этих жутких формул и продифференцировать. 🙂 Например, самую зверскую 7-ю формулу.

Всё нормально. Не обманули математики. 🙂

Ответ. Ничем не хуже.) Просто вышеназванные интегралы (от тангенса, логарифма, арксинуса и т.д.) не являются табличными. И встречаются на практике значительно реже, нежели те, что представлены в таблице. Поэтому знать наизусть, чему они равны, вовсе не обязательно. Достаточно лишь знать, как они вычисляются.)

Что, кому-то всё-таки невтерпёж? Так уж и быть, специально для вас!

Ну как, будете заучивать? 🙂 Не будете? И не надо.) Но не волнуйтесь, все подобные интегралы мы обязательно найдём. В соответствующих уроках. 🙂

Что ж, теперь переходим к свойствам неопределённого интеграла. Да-да, ничего не поделать! Вводится новое понятие — тут же и какие-то его свойства рассматриваются.

Свойства неопределённого интеграла.

Теперь не очень хорошая новость.

В отличие от дифференцирования, общих стандартных правил интегрирования, справедливых на все случаи жизни, в математике нету. Это фантастика!

Например, вы все прекрасно знаете (надеюсь!), что любое произведение любых двух функций f(x)·g(x) дифференцируется вот так:

Любое частное дифференцируется вот так:

А любая сложная функция, какой бы накрученной она ни была, дифференцируется вот так:

И какие бы функции ни скрывались под буквами f и g, общие правила всё равно сработают и производная, так или иначе, будет найдена.

А вот с интегралами такой номер уже не пройдёт: для произведения, частного (дроби), а также сложной функции общих формул интегрирования не существует! Нету никаких стандартных правил! Вернее, они есть. Это я зря математику обидел.) Но, во-первых, их гораздо меньше, чем общих правил для дифференцирования. А во-вторых, большинство методов интегрирования, о которых мы будем разговаривать в следующих уроках, очень и очень специфические. И справедливы лишь для определённого, очень ограниченного класса функций. Скажем, только для дробно-рациональных функций. Или каких-то ещё.

А какие-то интегралы, хоть и существуют в природе, но вообще никак не выражаются через элементарные «школьные» функции! Да-да, и таких интегралов полно! 🙂

Именно поэтому интегрирование — гораздо более трудоёмкое и кропотливое занятие, чем дифференцирование. Но в этом есть и своя изюминка. Занятие это творческое и очень увлекательное.) И, если вы хорошо усвоите таблицу интегралов и освоите хотя бы два базовых приёма, о которых мы поговорим далее ( замена переменной и интегрирование по частям ), то интегрирование вам очень понравится. 🙂

А теперь познакомимся, собственно, со свойствами неопределённого интеграла. Их всего ничего. Вот они.

Первые два свойства полностью аналогичны таким же свойствам для производных и называются свойствами линейности неопределённого интеграла. Тут всё просто и логично: интеграл от суммы/разности равен сумме/разности интегралов, а постоянный множитель можно вынести за знак интеграла.

А вот следующие три свойства для нас принципиально новые. Разберём их поподробнее. Звучат по-русски они следующим образом.

Третье свойство

Производная от интеграла равна подынтегральной функции

Конечно же, в ответе могут получаться настолько зверские и громоздкие функции, что и обратно дифференцировать их неохота, да. Но лучше, по возможности, стараться себя проверять. Хотя бы в тех примерах, где это несложно.)

Идём дальше, по порядочку.

Четвёртое свойство

Тут ничего особенного. Суть та же самая, только dx на конце появляется. Согласно предыдущему свойству и правилам раскрытия дифференциала.

Пятое свойство

Тоже очень простое свойство. Им мы тоже будем регулярно пользоваться в процессе решения интегралов. Особенно — в методе подведения функции под знак дифференциала и замены переменной .

Вот такие вот полезные свойства. Занудствовать с их строгими доказательствами я здесь не собираюсь. Желающим предлагаю это сделать самостоятельно. Прямо по смыслу производной и дифференциала. Докажу лишь последнее, пятое свойство, ибо оно менее очевидно.

Итак, у нас есть утверждение:

Вытаскиваем «начинку» нашего интеграла и раскрываем, согласно определению дифференциала:

На всякий случай, напоминаю, что, согласно нашим обозначениям производной и первообразной, F’(x) = f(x).

Вставляем теперь наш результат обратно внутрь интеграла:

Получено в точности определение неопределённого интеграла (да простит меня русский язык)! 🙂

Что ж. На этом наше начальное знакомство с таинственным миром интегралов считаю состоявшимся. На сегодня предлагаю закруглиться. Мы уже достаточно вооружены, чтобы идти в разведку. Если не пулемётом, то хотя бы водяным пистолетом базовыми свойствами и таблицей. 🙂 В следующем уроке нас уже ждут простейшие безобидные примеры интегралов на прямое применение таблицы и выписанных свойств.

Источник