что такое периодическое движение в физике

Что такое периодическое движение в физике

Если положение автомобиля меняется относительно домов или деревьев, то говорят, что он движется относительно этих тел.

Путь- это длина траектории.

Перемещение- это вектор направленный из начального положение в конечное.

Виды механического движения.

Равномерное, неравномерное и прямолинейное движение.

По разным признакам можно выделить разные виды механического движения.

Равномерное движение встречается очень редко. Почти равномерно движется Земля вокруг Солнца, проходя приблизительно равные пути за одинаковое время.

Неравномерное движение- если тело проходит за равные промежутки времени разные пути.

При поступательном движении любая линия, проведенная на теле, будет перемещаться параллельно самой себе.

Если тело движется поступательно то его тоже можно считать материальной точкой.

Например, проведем несколько линий на игрушечном автомобиле и переместим его из одной точки в другую. На всех участках траектории автомобиль совершает поступательное движение.

Источник

Что такое периодическое движение в физике

Периодические процессы характеризуются последовательностью состояний, через которые проходит система в течение одного периода. Если эта последовательность точно повторяется через равные промежутки времени, то колебания называются незатухающими. При нарастающих или затухающих колебаниях периодически повторяются только определенные состояния системы, например прохождение колеблющегося тела через положение равновесия и т. п.

Среди множества различных незатухающих колебаний простейшим является гармоническое колебательное движение, описываемое функцией синуса или косинуса:

Во всех случаях, когда рассматривается одно колебание, можно выбрать начало отсчета времени так, чтобы однако при одновременном существовании нескольких колебаний (например, при сложении колебаний) начальные фазы каждого колебания отличаются друг от друга и лишь в частных случаях эти фазы могут одновременно равняться нулю.

Формула (4.1) описывает гармонические колебательные движения, происходящие вдоль какой-нибудь линии — отрезка прямой или кривой. В этом случае для определения положения колеблющегося тела достаточно задать только расстояние х от тела до положения равновесия. Колебательные системы, в которых возможно только одно

колебательное движение (вдоль одной линии), изображены на рис. 1.37; их называют колебательными системами с одной степенью свободы. Простой маятник (см. рис. 1.36, а) может совершать два независимых друг от друга колебания в двух взаимно перпендикулярных направлениях, поэтому его относят к колебательным системам, обладающим двумя степенями свободы. Пружинный маятник, изображенный на рис. 1.36, б, может колебаться в трех независимых направлениях и поэтому является колебательной системой с тремя степенями свободы.

Для описания колебательного движения сплошного твердого тела (рис. 1.38, а) удобнее измерять углы поворота а от равновесного состояния; углы, отсчитываёмые по одну сторону от , принимаются положительными, по другую сторону — отрицательными. Аналогичное правило знаков выбирается и для тел, совершающих так называемые крутильные колебания (рис. 1.38, б). Гармонические колебания для углов поворота имеют вид где амплитуда угла поворота.

Источник

§ 1. Колебательное движение. Гармонические колебания

1. Какое движение называют периодическим? Колебательным?

Движение называют периодическим, если физические величины, характеризующие движение, принимают одни и те же значения через равные промежутки времени. Колебательным движение называют движение, которое неоднократно повторяется
по одной и той же траектории.

2. Что называют амплитудой колебаний? Периодом? Частотой?

Амплитудой колебаний называют максимальное отклонение маятника от положения равновесия.

Периодом колебаний называют минимальный промежуток времени, в течение которого повторяются значения всех физических величин этого колебания, т.е. совершается одно полное колебание.

Частотой колебаний называют число колебаний, которое совершает тело в единицу времени.

3. Каким соотношением связаны между собой частота колебаний ν и циклическая частота колебаний ω?

Частота и циклическая частота колебаний связаны между собой соотношение:

4. Что такое кинематический закон движения? Запишите закон движения при гармонических колебаниях.

Кинематический закон движения — это зависимость координаты от времени x(t).

Закон движения при гармонических колебаниях:

по закону косинуса:

5. Какой путь проходит гармонически колеблющееся тело за два периода колебаний, если амплитуда колебаний равна A?

За два периода тело пройдёт расстояние 4А, поскольку за один период тело проходит расстояние, равное двум амплитудам.

6. Приведите примеры колебательных систем в природе и технике.

Колебательные системы в природе: землетрясения, приливы и отливы.

Колебательные системы в технике: маятниковые часы, детские качели.

Источник

Презентация «Кинематика периодического движения»

Ищем педагогов в команду «Инфоурок»

Тема: «КИНЕМАТИКА ПЕРИОДИЧЕСКОГО ДВИЖЕНИЯ»

Цель : знать законы периодического движения, уметь применять и на практике

Оборудование: компьютер, экран, проектор, планетарная модель земли.

СЛ.1.«КИНЕМАТИКА ПЕРИОДИЧЕСКОГО ДВИЖЕНИЯ»

Периодическое движение – движение, повторяющееся через равные промежутки времени.

Виды периодического движения:

Вращательное движение –движение в одном направлении по замкнутой траектории

( например, движение спутника вокруг земли)

Колебательное движение-движение вдоль одного и того же отрезка с изменением направления движения

(Например, колебания поплавка на поверхности воды)

(Например, колебания крыльев комара, колебание)

Сл. 6 РАВНОМЕРНОЕ ДВИЖЕНИЕ ПО ОКРУЖНОСТИ

(Рисунок в презентации)

-Ускорение при равномерном движении по окружности направлено к центру окружности и называется центростремитель-ным

-Скорость тела при равномерном движении по окружности не меняется по модулю, меняется по направлению, направлена по касательной к окружности

-Скорость тела всегда остается перпендикулярной ускорению

Сл. 7 ХАРАКТЕРИСТИКИ РАВНОМЕРНОГО ДВИЖЕНИЯ ПО ОКРУЖНОСТИ

T =2П R / V (единица измерения- секунда)

Фаза вращения – угол поворота радиус-вектора тела в произвольный момент времени

а ( единица измерения- радиан)

Угловая скорость – физическая величина, равная отношению угла поворота тела к промежутку времени, в течение которого этот поворот произошел

W = a / t (единица измерения радиан/секунда)

Сл.8 СВЯЗЬ ЛИНЕЙНОЙ И УГЛОВОЙ СКОРОСТИ ДВИЖЕНИЯ ПО ОКРУЖНОСТИ

T =2П R / V период вращения

Т=2П/ W период вращения

2П R / V =2П/ W то есть V = WR

— колебания, при которых колеблющееся величина изменяется со временем синусоидально (косинусоидально).

Найти линейную скорость вращения Земли вокруг Солнца с радиусом R = 1.5*10 8 км. Период= 1 год.

-вывод по материалу.

5. Домашнее задание.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс профессиональной переподготовки

Физика: теория и методика преподавания в образовательной организации

Курс повышения квалификации

Современные педтехнологии в деятельности учителя

Номер материала: ДВ-033676

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

Заболеваемость ковидом среди студентов и преподавателей снизилась на 33%

Время чтения: 4 минуты

В Москве запустили онлайн-проект по борьбе со школьным буллингом

Время чтения: 2 минуты

Путин попросил привлекать родителей к капремонту школ на всех этапах

Время чтения: 1 минута

В России выбрали топ-10 вузов по работе со СМИ и контентом

Время чтения: 3 минуты

Минобрнауки разработало концепцию преподавания истории российского казачества

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Периодическое движение: вращение и колебание

Пока я смотрел прямо вверх (маятник приходился как раз надо мною), мне почудилось, что он двигается. Минуту спустя впечатление подтвердилось. Ход маятника был короткий и, разумеется, медленный. Несколько мгновений я следил за ним с некоторым страхом, но скорей с любопытством. Наконец, наскуча его унылым качанием, я решил оглядеться.

Э. По. Колодец и маятник

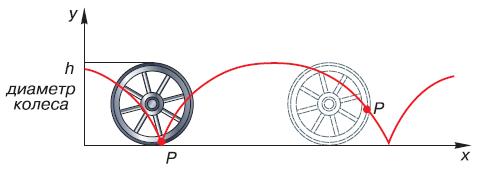
Теперь познакомимся с тем, что происходит, если тело движется прямолинейно и одновременно с этим участвует во вращательном движении. Представьте себе, что катится колесо. Мы уже говорили, что при этом его единственная точка, а именно центр, движется прямолинейно, а остальные, наряду с этим поступательным движением, движутся по окружности вокруг этого центра. Какие траектории будут описывать эти точки, например точка, находящаяся на ободе колеса? Рассмотрим это на графике, где по оси x отложим положение точки относительно места начала её движения, а по оси у – её высоту над землёй (рис. 55). Мы видим, что эта высота меняется в пределах от нуля до размеров диаметра колеса. По мере того как колесо катится всё дальше, высота положения точки на его ободе постепенно повышается, затем начинает плавно снижаться до нуля и снова постепенно повышаться. Такое движение называют периодическим.

Вращение.

Для того чтобы наблюдать периодические движения, необязательно, чтобы тела передвигались в пространстве вдоль прямой линии. В некоторых случаях достаточно, чтобы они просто вращались. В этом легко убедиться, посмотрев на обычные часы. Их стрелки вращаются вокруг оси, и при этом мы замечаем, что они периодически возвращаются в одну и ту же точку циферблата. Можно построить график, аналогичный предыдущему, но теперь по оси x отложить уже не расстояние, а время. По оси у отложим цифры, на которые указывает стрелка. Правда, может возникнуть проблема: как измерять отрезки времени? Этого нельзя сделать по нашим часам, поскольку с их помощью мы измеряем движение стрелок самих часов.

Рис. 55. Траектория движения точки оси и обода колеса при его качении

Для этой цели нужно воспользоваться другими часами, например песочными. Также можно считать свой пульс, как это делал Галилей, или просто довериться внутреннему ощущению времени, о котором мы говорили в предыдущей главе. В любом случае мы знаем, что время проходит, правильнее сказать, длится. И по мере того как оно длится, стрелки на циферблате часов меняют своё положение от 1 до 12, снова от 1 до 12 и так всё время, пока мы будем наблюдать. Но если часы имеют три стрелки – часовую, минутную и секундную, то они будут возвращаться в исходное положение, скажем, к цифре 1, через неодинаковое время. Секундной стрелке для этого понадобится 60 с, минутной – час, т. е. 3600 с, а часовой – 12 ч, т. е. 43 200 с. Это означает, что разные стрелки имеют различные периоды обращения, которые равны соответственно минуте, часу и 12 часам. Такое движение называют периодическим, и мы его уже обсуждали в предыдущем параграфе. По завершении цикла – полного оборота стрелки – она возвращается в исходное положение, и всё начинается сначала. Но это начало будет началом только с точки зрения этой стрелки, а с точки зрения других – процесс будет продолжаться. Если у нас есть часы с разными стрелками, мы можем не пользоваться для отсчёта никакими другими часами, а просто построить график, отложив по оси х показания минутной стрелки, а по оси у – секундной. Ровно через минуту секундная стрелка вернётся в исходное положение и начнёт отсчёт сначала, а минутная сдвинется только на одно деление и будет отсчитывать всё новые отрезки времени. Посмотрев на график, мы увидим, что на нём изображена периодическая функция. Через равные отрезки на оси х, соответствующие минуте, точка будет иметь одинаковые значения, если отсчитывать их по оси х. Мы получили периодическое движение с периодом , составляющим 1 мин.

Под периодическими процессами понимают такие изменения в системах, когда их положение или состояние через определённый промежуток времени возвращается к тому, которое уже имело место раньше. Самым наглядным периодическим процессом служит движение Земли вокруг своей оси и вокруг Солнца. С интервалом в 24 ч Солнце появляется над горизонтом, проходит через зенит и исчезает за другой точкой горизонта. С интервалом приблизительно в 365 дней меняется температура воздуха, распускаются и опадают листья, празднуется день рождения, начинается и кончается учебный год. Но эти примеры хотя и наглядны, но не совсем точны. Солнце сегодня восходит и заходит не совсем в тех точках, где оно это делало вчера, листья в этом году могут распуститься раньше или позже, чем в предыдущем, да и вообще Земля оборачивается вокруг Солнца не за 365 дней, а несколько медленнее. Так что такая периодичность, в отличие от периодичности точных физических процессов, имеет приблизительный характер. Но именно чередование времени суток и времён года послужило для человечества началом измерения времени, создания календаря и внесло порядок в хозяйственное и социальное устройство.

Колебания.

Математический маятник. Процесс колебания математического маятника выглядит следующим образом (рис. 56). Отведём груз на некоторое расстояние. Тогда на него будет действовать сила тяжести, направленная вертикально вниз, и сила натяжения нити. В результате сложения этих сил груз будет совершать движение по дуге. Оказавшись в самой низкой точке, он достигнет положения равновесия. Но он не останавливается, а по инерции продолжает своё движение по дуге, но уже поднимаясь вверх. Так как ускорения во время снижения и во время подъёма равны по модулю, высота этой точки будет в точности равна той, с которой маятник начал своё снижение. Поэтому весь процесс движения повторяется, но в обратном направлении. При отсутствии трения эти колебания будут продолжаться бесконечно.

Пружинный маятник. Пружинный маятник похож по принципу действия на математический, но вместо гравитации в нём действует сила упругости пружины. Если закрепить груз на горизонтальной пружине, а затем эту пружину растянуть, то сила упругости будет пропорциональна удлинению пружины (рис. 57). Под действием этой силы груз начнёт двигаться вверх к положению равновесия. Но, дойдя до точки равновесия, он не остановится, а будет по инерции продолжать двигаться в противоположную сторону, сжимая пружину. Упругая сила сжимаемой пружины сначала остановит груз, а потом заставит его двигаться в обратном направлении, пока он не вернётся в исходную точку.

Рис. 56. Разложение сил при колебании маятника

Там на груз опять будет действовать сила растянутой пружины, и колебательный процесс будет продолжаться.

Источник