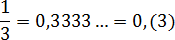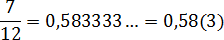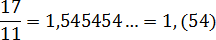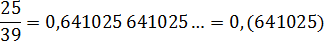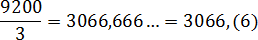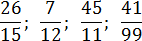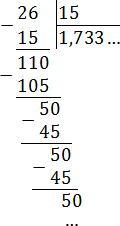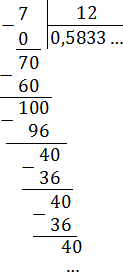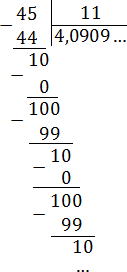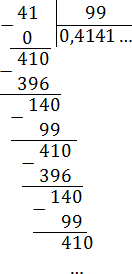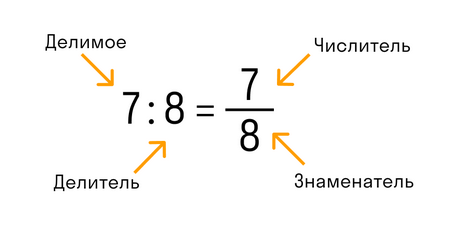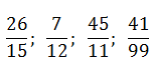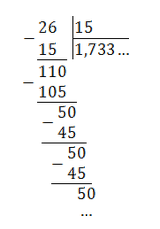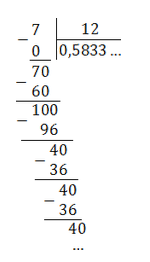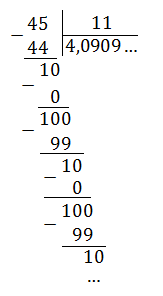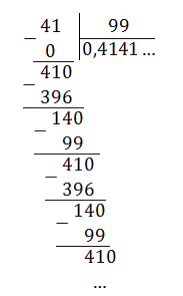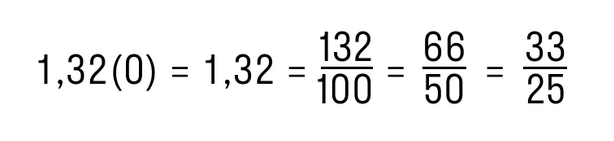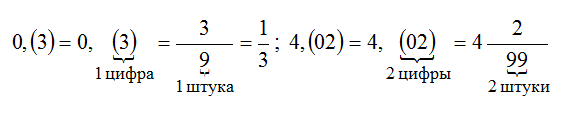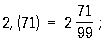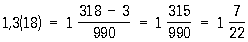что такое период дроби
Периодические десятичные дроби
Помните, как в самом первом уроке про десятичные дроби я говорил, что существуют числовые дроби, не представимые в виде десятичных (см. урок «Десятичные дроби»)? Мы еще учились раскладывать знаменатели дробей на множители, чтобы проверить, нет ли там чисел, отличных от 2 и 5.
Так вот: я наврал. И сегодня мы научимся переводить абсолютно любую числовую дробь в десятичную. Заодно познакомимся с целым классом дробей с бесконечной значащей частью.
— это любая десятичная дробь, у которой:
Поскольку определений много, стоит подробно рассмотреть несколько таких дробей:
Эта дробь встречается в задачах чаще всего. Непериодическая часть: 0; периодическая часть: 3; длина периода: 1.
Непериодическая часть: 0,58; периодическая часть: 3; длина периода: снова 1.
Непериодическая часть: 1; периодическая часть: 54; длина периода: 2.
Непериодическая часть: 0; периодическая часть: 641025; длина периода: 6. Для удобства повторяющиеся части отделены друг от друга пробелом — в настоящем решении так делать не обязательно.
Непериодическая часть: 3066; периодическая часть: 6; длина периода: 1.
Как видите, определение периодической дроби основано на понятии значащей части числа. Поэтому если вы забыли что это такое, рекомендую повторить — см. урок «Умножение и деление десятичных дробей».
Переход к периодической десятичной дроби
Рассмотрим обыкновенную дробь Разложим ее знаменатель на простые множители. Возможны два варианта:
Чтобы задать периодическую десятичную дробь, надо найти ее периодическую и непериодическую часть. Как? Переведите дробь в неправильную, а затем разделите числитель на знаменатель «уголком».
При этом будет происходить следующее:
Вот и все! Повторяющиеся цифры после десятичной точки обозначаем периодической частью, а то, что стоит спереди — непериодической.
Задача. Переведите обыкновенные дроби в периодические десятичные:
Все дроби без целой части, поэтому просто делим числитель на знаменатель «уголком»:
Как видим, остатки повторяются. Запишем дробь в «правильном» виде:
В итоге получается дробь:
Записываем в нормальном виде:
Переход от периодической десятичной дроби к обыкновенной
Рассмотрим периодическую десятичную дробь Требуется перевести ее в классическую «двухэтажную». Для этого выполним четыре простых шага:
Задача. Приведите к обыкновенной неправильной дроби числа:
Работаем с первой дробью:
В скобках содержится лишь одна цифра, поэтому период Далее умножаем эту дробь Имеем:
Вычитаем исходную дробь и решаем уравнение:
Теперь разберемся со второй дробью. Итак,
Период k = 2, поэтому умножаем все
Снова вычитаем исходную дробь и решаем уравнение:
100 X − X =
99 X = 3207;
X = 3207/99 = 1069/33.
Приступаем к третьей дроби: Схема та же самая, поэтому я просто приведу выкладки:
Период k = 1 ⇒ умножаем все на 10 k = 10 1 = 10;
Наконец, последняя дробь: Опять же, для удобства периодические части отделены друг от друга пробелами. Имеем:
Бесконечные периодические десятичные дроби
В данной публикации мы рассмотрим, что из себя представляют бесконечные периодические десятичные дроби, какие бывают виды, и как их можно перевести в обыкновенную дробь. Также разберем примеры для закрепления материала.
Периодические десятичные дроби
Определение
Если в дробной части бесконечной десятичной дроби есть один или несколько цифр, которые повторяются в одной и той же последовательности, такая дробь является периодической.
Примеры периодических десятичных дробей:
Запись
Повторяющаяся цифра/цифры – это период дроби, который пишется в скобке для сокращения длины записи. Например, дроби выше сокращенно следует писать так:
Произношение
Чистые периодические дроби – это такие бесконечные десятичные дроби, период которых начинается сразу после запятой.
Смешанные периодические дроби – бесконечные десятичные дроби, у которых между запятой и периодом присутствует одна и более цифр (их количество ограничено).
Перевод периодической десятичной дроби в обыкновенную
Для того, чтобы перевести периодическую дробь в обыкновенную (простую), выполняем следующие шаги:
Пример 1
Давайте переведем число 0,8(3) в обыкновенную дробь.
Действовать будет пошагово согласно инструкции выше:
1. n = 1
2. m = 1
3. a = 83
4. b = 8
5. x = 0
6. Остается только применить формулу:
Пример 2
Представим периодическую дробь 2,64(378) в виде обыкновенной.
1. n = 3
2. m = 2
3. a = 64378
4. b = 64
5. x = 2
6. Подставляем эти значения в формулу нахождения простой дроби и получаем:
Как перевести периодическую дробь
Определение дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
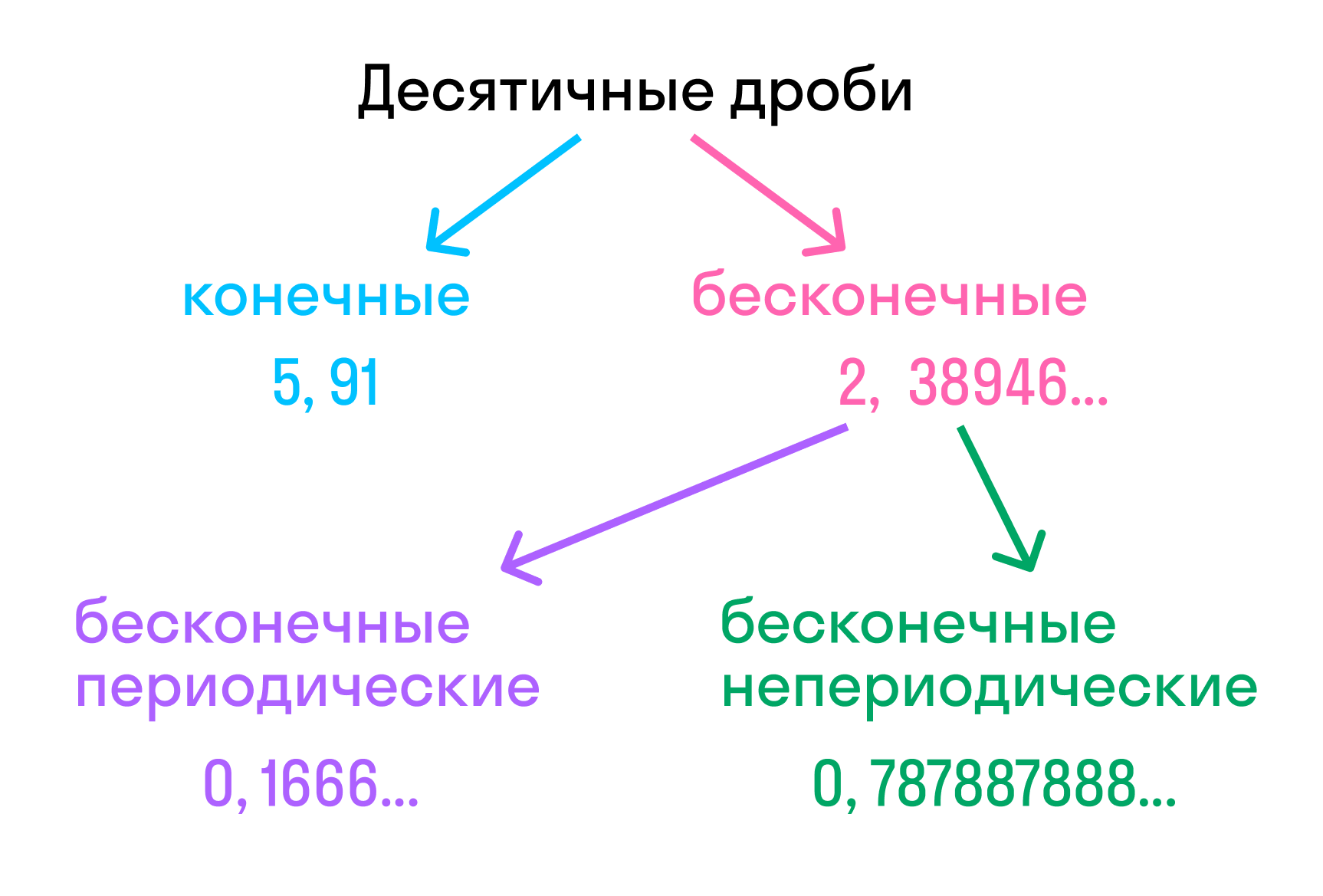
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Переход к периодической десятичной дроби
Рассмотрим обыкновенную дробь вида a/b. Разложим ее знаменатель на простые множители. Тут есть два варианта:
Чтобы задать периодическую десятичную дробь, нужно найти ее периодическую и непериодическую часть. Чтобы это сделать нужно привести дробь в неправильную, а затем разделить числитель на знаменатель столбиком.
Что будет происходить в процессе:
Повторяющиеся цифры после десятичной точки нужно обозначить периодической частью, а то, что стоит спереди — непериодической.
Пример. Перевести обыкновенные дроби в периодические десятичные:
Все дроби без целой части, поэтому просто делим числитель на знаменатель уголком:
Определение периодической дроби
Периодическая дробь — это бесконечная десятичная дробь, в которой, начиная с некоторого места, периодически повторяется определенная группа цифр.
Периодическая часть дроби — это набор повторяющихся цифр, из которых состоит значащая часть.
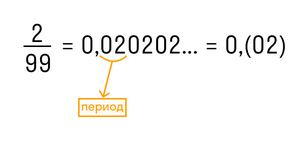
В краткой записи периодической дроби повторяющиеся цифры пишут в скобках и называют периодом дроби. Например, вместо 1,555… записывают 1,(5) и читают «одна целая и пять в периоде».
Остальной отрезок значащей части, который не повторяется, называется непериодической частью.
Виды периодических дробей: чистые и смешанные.
Чистая периодическая десятичная дробь — это десятичная дробь, в записи которой сразу после запятой следует период. Например: 1,(4); 4,(25); 21,(693).
Смешанная периодическая десятичная дробь — это десятичная дробь, в записи которой после запятой через одну или несколько цифр начинается период. Например: 3,5(1); 0,02(89); 7,0(123) и т.д.
Рассмотрим примеры дробей, чтобы научиться определять части и период.
Непериодическая часть: 0; периодическая часть: 3; длина периода: 1.
Читаем так: ноль целых три в периоде.
7/12 = 0,583333. = 0,58(3)
Непериодическая часть: 0,58; периодическая часть: 3; длина периода: снова 1.
Читаем так: ноль целых пятьдесят восемь сотых и три в периоде.
17/11 = 1,545454. = 1,(54)
Непериодическая часть: 1; периодическая часть: 54; длина периода: 2.
Читаем так: одна целая пятьдесят четыре сотых в периоде.
25/39 = 0,641025 641025. = 0,(641025)
Непериодическая часть: 0; периодическая часть: 641025; длина периода: 6.
Читаем так: ноль целых шестьсот сорок одна двадцать пять миллионных в периоде.
пятьдесят четыре сотых в периоде.
9200/3 = 3066,666. = 3066,(6)
Непериодическая часть: 3066; периодическая часть: 6; длина периода: 1.
Читаем так: три тысячи шестьдесят шесть целых и шесть в периоде.
Перевод периодической дроби в обыкновенную
Давайте разберемся, как перевести периодическую десятичную дробь в обыкновенную дробь.
Если период дроби равен нулю, значит решение будет быстрым. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби.
Пример. Преобразуем периодическую дробь 1,32(0) в обыкновенную.
Для этого отброс им нули справа и получим конечную десятичную дробь 1,32. Далее следуем алгоритму из предыдущих пунктов:
Рассмотрим пример, в котором период дроби отличен от нуля.
Как записать периодическую дробь 10,0219(37) в виде обыкновенной:
В нашем примере k = 2.
Если вначале, до первой значащей цифры, идут нули, то отбрасываем их. Обозначим полученное число — a.
Теперь осталось подставить все найденные значения в формулу и получить ответ:
Вот так мы справились с задачей представить бесконечную периодическую дробь в виде обыкновенной.
Есть еще один способ преобразовать периодическую дробь в обыкновенную. Для этого нужно рассматреть периодическую часть как сумму членов геометрический прогрессии, которая убывает. Например, вот так:
Для суммы членов бесконечной убывающей геометрической прогрессии есть формула. Если первый член прогрессии равен b, а знаменатель q таков, что 0
Перевод чистой периодической дроби в обыкновенную
Напомним: отличие чистой периодической десятичной дроби в том, что в ней сразу после запятой следует период.
Чтобы обратить чистую периодическую дробь в обыкновенную, достаточно записать числителем ее период, а в знаменателе записать столько девяток, сколько цифр в периоде. Вот так:
Перевод смешанной периодической дроби в обыкновенную
Отличие смешанной периодической десятичной дроби в том, что после запятой через одну или несколько цифр начинается период.
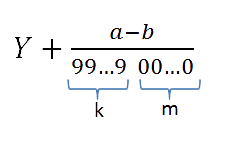
Чтобы записать смешанную периодическую дробь в виде обыкновенной, нужно из числа, которое стоит до второго периода вычесть число, стоящее до первого периода, и записать результат в числителе.
А в знаменатель нужно поставить число, которое содержит столько девяток, сколько цифр в периоде, нулей в конце и сколько цифр между запятой и периодом.
Например, запишем 2,34(2) в виде обыкновенной дроби:
Алгебра. 7 класс
Конспект урока
Периодические десятичные дроби. Периодичность десятичного разложения обыкновенной дроби
Перечень рассматриваемых вопросов:
Понятие бесконечной периодической десятичной дроби.
Примеры бесконечной периодической десятичной дроби.
Представление рационального числа в видебесконечной периодической десятичной дроби.
Любое целое число и любую конечную десятичную дробь можно считать бесконечной периодической десятичной дробью или коротко: периодической дробью.
Любое положительное рациональное число
преобразуется в положительную дробь.
Любая периодическая дробь – это десятичное разложение некоторого положительного рационального числа
Если в периодической дроби период начинается сразу после запятой, то такую периодическую дробь называют «чистой».
Если в периодической дроби период начинается не сразу, а после некоторого количества не повторяющихся цифр, то такую периодическую дробь называют «смешанной».
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
На прошлом уроке мы рассмотрели условия, при которых обыкновенную дробь можно представить в виде конечной десятичной.
А как поступать, когда невозможно представить её в таком виде?
Введём понятие бесконечной периодической десятичной дроби.
Если знаменатель q несократимой дроби p/q не имеет делителей, кроме 2 и 5, то эта дробь преобразуется в конечную десятичную дробь.
Если знаменатель содержит, кроме 2 и 5, другие простые делители, то мы не сможем представить её конечной десятичной дробью.
Знаменатель 9 = 3 3
5/9 не преобразуется в конечную десятичную дробь. Убедимся в этом, выполнив деление уголком.
Разделим числитель 5 на знаменатель 9.
Процесс деления в столбик бесконечный. Приходим к выражению 0,555…,
точки означают, что цифра 5 периодически повторяется бесконечно много раз.
Выражение 0,555… называют бесконечной периодической десятичной дробью или коротко: периодической дробью.
Читают: « ноль целых и пять в периоде».
Цифру (5) называют периодом дроби 0,(5).
Говорят, что число пять девятых представлено в виде периодической дроби ноль целых и пять в периоде.
Выражение 5/9 и 0,(5) являются обозначениями одного и того же числа в виде обыкновенной дроби 5/9 и в виде периодической дроби 0,(5).
Рассмотрим ещё пример.
Дробь четыре пятнадцатых несократимая, и её знаменатель имеет простые делители 3 и 5, поэтому деление не может быть конечным. Проверим.
Делим уголком 4 на 15.
читают: «ноль целых две десятых и шесть в периоде».
В примерах мы увидели разные периодические дроби.
Периодические дроби бывают двух видов: «чистые» и «смешанные».
Если в периодической дроби период начинается сразу после запятой, то такую периодическую дробь называют «чистой».
Видно, что в этих дробях период начинается сразу после запятой.
Если же в периодической дроби период начинается не сразу, а после некоторого количества не повторяющихся цифр, то такую периодическую дробь называют «смешанной».
Если применить правило деления уголком к любой несократимой дроби p/q
Где q – знаменатель, который, кроме 2 и 5 имеет другие простые делители, то получится бесконечная периодическая десятичная дробь, или коротко: периодическая дробь.
Приписывая к конечной десятичной дроби бесконечно много нулей, мы её приводим в бесконечную периодическую десятичную дробь с периодом 0.
45 = 45,0 = 45,000… = 45,(0)
0,673 = 0,673000 = 0,673(0).
Значит, любое целое число и любую конечную десятичную дробь можно считать бесконечной периодической десятичной дробью или коротко: периодической дробью.
Любое положительное рациональное число p/q преобразуется в периодическую дробь.
Верно обратное. Любая периодическая дробь – это десятичное разложение некоторого положительного рационального числа p/q.
Периодичность десятичного разложения обыкновенной дроби
Рассмотрим произвольную положительную несократимую дробь p/q
Покажем, что если разделить числитель дроби на знаменатель уголком, то в частном получится либо конечное, либо бесконечное периодическое её преобразование.
Нам известно, чтобы получить конечное десятичное разложение, знаменатель qне должен иметь простых делителей, кроме 2 и 5
В других случаях может быть только бесконечное десятичное разложение, которое является периодическим. Пусть нужно найти десятичное разложение несократимой дроби 15/13.
Будем делить уголком 15 на 13.
Здесь одной звёздочкой отмечен этап вычислений, когда снесена последняя цифра делимого. Получаемые после этого остатки заключены в прямоугольники. Видно, что остатки, отмеченные двумя, тремя звёздочками, равны между собой. Это показывает, что процесс деления носит периодический характер и приводит к бесконечной периодической десятичной дроби, то есть:
Теперь на примере рассмотрим, как можно, зная бесконечную периодическую десятичную дробь, записать её обыкновенной дробью.
Запишем периодическую дробь 0,(7) в виде обыкновенной.
Для этого обозначим искомую величину х. Тогда справедливо равенство
Умножим это равенство на 10, получим
Вычтем из равенства (2) равенство (1).
Применив к дроби 7/9 деление уголком. Снова получим периодическую дробь 0, (7.)
Разбор заданий тренировочного модуля.
Подберите обыкновенную дробь, равную периодической десятичной 0,(14).
Варианты ответов: 14/99, 14/98 14/90
Обозначим искомую величину х. Тогда справедливо равенство:
Умножим это равенство на 100, получим
Вычтем из равенства (2) равенство (1).
Найдите десятичное разложение обыкновенной дроби 769/4950
Решение: Для решения задачи нужно выполнить деление уголком:
Периодическая дробь
Полезное
Смотреть что такое «Периодическая дробь» в других словарях:
ПЕРИОДИЧЕСКАЯ ДРОБЬ — бесконечная десятичная дробь, в которой, начиная с некоторого места, периодически повторяется определенная группа цифр (период), напр. 0,373737. чисто периодическая дробь или 0,253737. смешанная периодическая дробь … Большой Энциклопедический словарь
периодическая дробь — дробь, бесконечная дробь Словарь русских синонимов. периодическая дробь сущ., кол во синонимов: 2 • бесконечная дробь (2) • … Словарь синонимов
ПЕРИОДИЧЕСКАЯ ДРОБЬ — десятичная дробь, ряд цифр которой повторяется в одном и том же порядке. Например, 0,135135135… есть п. д., которой период 135 и которая равна простой дроби 135/999 = 5/37. Словарь иностранных слов, вошедших в состав русского языка. Павленков Ф … Словарь иностранных слов русского языка
Периодическая дробь — Десятичная дробь дробь со знаменателем 10n, где n натуральное число. Имеет особую форму записи: целая часть в десятичной системе счисления, затем запятая и затем дробная часть в десятичной системе счисления, причём количество цифр дробной части … Википедия
периодическая дробь — бесконечная десятичная дробь, в которой, начиная с некоторого места, периодически повторяется определённая группа цифр (период); например, 0,373737. чисто периодическая дробь или 0,253737. смешанная периодическая дробь. * * * ПЕРИОДИЧЕСКАЯ… … Энциклопедический словарь
ПЕРИОДИЧЕСКАЯ ДРОБЬ — бесконечная десятичная дробь, в к рой, начиная с нек рого места, периодически повторяется определ. группа цифр (период); напр., 0,373737. чисто П. д. или 0,253737. смешанная П. д … Естествознание. Энциклопедический словарь
дробь — См. часть. Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. дробь мелочь, часть; дунст, шарик, шрот, картечь; дробное число Словарь русских синонимов … Словарь синонимов
периодическая десятичная дробь — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN circulating decimalrecurring decimalperioding decimalperiodic decimalperiodical decimal … Справочник технического переводчика
Дробь — Если делится какое нибудь целое число а на другое целое число b, т. е. ищется число x, удовлетворяющее условию bx=а, то могут представиться два случая: или в ряду целых чисел найдется число х, которое этому условию удовлетворит, или же окажется,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Десятичная дробь — дробь, знаменатель которой есть целая степень числа 10. Д. д. пишут без знаменателя, отделяя в числителе справа запятой столько цифр, сколько нулей содержится в знаменателе. Например, В такой записи часть, стоящая слева… … Большая советская энциклопедия