что такое переобучение в машинном обучении
Переобучение
Переобучение (англ. overfitting) — негативное явление, возникающее, когда алгоритм обучения вырабатывает предсказания, которые слишком близко или точно соответствуют конкретному набору данных и поэтому не подходят для применения алгоритма к дополнительным данным или будущим наблюдениям.
Недообучение (англ. underfitting) — негативное явление, при котором алгоритм обучения не обеспечивает достаточно малой величины средней ошибки на обучающей выборке. Недообучение возникает при использовании недостаточно сложных моделей.
Содержание
Примеры [ править ]
На примере линейной регрессии [ править ]
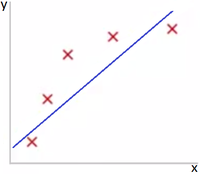
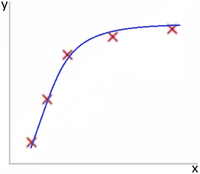
Представьте задачу линейной регрессии. Красные точки представляют исходные данные. Синие линии являются графиками полиномов различной степени M, аппроксимирующих исходные данные.
Как видно из Рис. 1, данные не поддаются линейной зависимости при небольшой степени полинома и по этой причине модель, представленная на данном рисунке, не очень хороша.
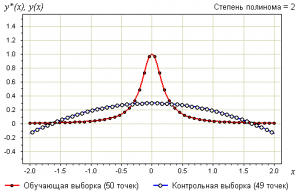
На Рис. 2 представлена ситуация, когда выбранная полиномиальная функция подходит для описания исходных данных.
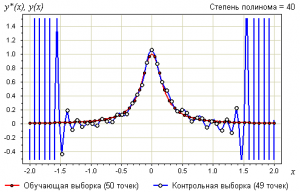
Рис. 3 иллюстрирует случай, когда высокая степень полинома ведет к тому, что модель слишком заточена на данные обучающего датасета.
На примере логистической регрессии [ править ]
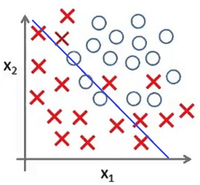
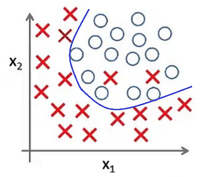
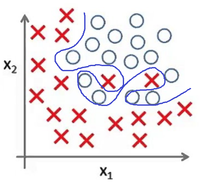
Представьте задачу классификации размеченных точек. Красные точки представляют данные класса 1. Голубые круглые точки — класса 2. Синие линии являются представлением различных моделей, которыми производится классификация данных.
Рис. 4 показывает результат использования слишком простой модели для представленного датасета
Кривые обучения [ править ]
Кривые обучения при переобучении [ править ]
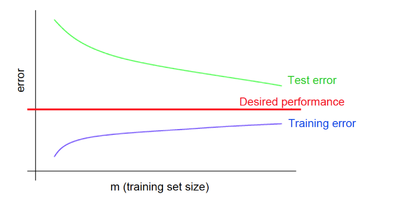
При переобучении небольшая средняя ошибка на обучающей выборке не обеспечивает такую же малую ошибку на тестовой выборке.
Рис. 7 демонстрирует зависимость средней ошибки для обучающей и тестовой выборок от объема датасета при переобучении.
Кривые обучения при недообучении [ править ]
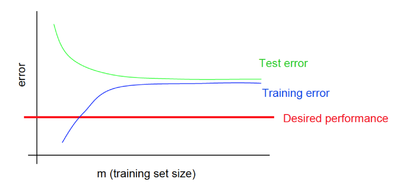
При недообучении независимо от объема обучающего датасета как на обучающей выборке, так и на тестовой выборке небольшая средняя ошибка не достигается.
Рис. 8 демонстрирует зависимость средней ошибки для обучающей и тестовой выборок от объема датасета при недообучении.
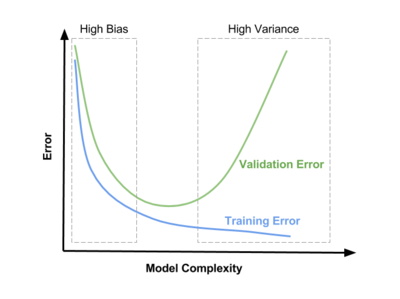
High variance и high bias [ править ]
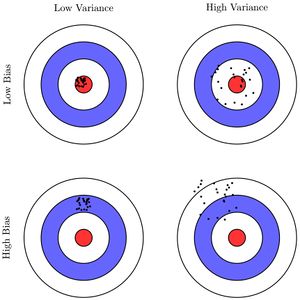
Bias — ошибка неверных предположений в алгоритме обучения. Высокий bias может привести к недообучению.
Variance — ошибка, вызванная большой чувствительностью к небольшим отклонениям в тренировочном наборе. Высокая дисперсия может привести к переобучению.
При использовании нейронных сетей variance увеличивается, а bias уменьшается с увеличением количества скрытых слоев.
Для устранения high variance и high bias можно использовать смеси и ансамбли. Например, можно составить ансамбль (boosting) из нескольких моделей с высоким bias и получить модель с небольшим bias. В другом случае при bagging соединяются несколько моделей с низким bias, а результирующая модель позволяет уменьшить variance.
Дилемма bias–variance [ править ]
Дилемма bias–variance — конфликт в попытке одновременно минимизировать bias и variance, тогда как уменьшение одного из негативных эффектов, приводит к увеличению другого. Данная дилемма проиллюстрирована на Рис 10.
При небольшой сложности модели мы наблюдаем high bias. При усложнении модели bias уменьшается, но variance увеличится, что приводит к проблеме high variance.
Переобучение
Материал из MachineLearning.
Содержание
Обобщающая способность (generalization ability, generalization performance). Говорят, что алгоритм обучения обладает способностью к обобщению, если вероятность ошибки на тестовой выборке достаточно мала или хотя бы предсказуема, то есть не сильно отличается от ошибки на обучающей выборке. Обобщающая способность тесно связана с понятиями переобучения и недообучения.
Переобучение, переподгонка (overtraining, overfitting) — нежелательное явление, возникающее при решении задач обучения по прецедентам, когда вероятность ошибки обученного алгоритма на объектах тестовой выборки оказывается существенно выше, чем средняя ошибка на обучающей выборке. Переобучение возникает при использовании избыточно сложных моделей.
Недообучение — нежелательное явление, возникающее при решении задач обучения по прецедентам, когда алгоритм обучения не обеспечивает достаточно малой величины средней ошибки на обучающей выборке. Недообучение возникает при использовании недостаточно сложных моделей.
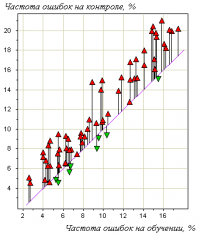
Пример. На рисунке справа показан эффект переобучения в одной задаче медицинского прогнозирования. Точки на графике соотвествуют различным методам обучения. Каждая точка получена путём усреднения по большому числу разбиений исходной выборки из 72 прецедентов на обучающую подвыборку и контрольную. Горизонтальная ось — частота ошибок на обучении; вертикальная — на контроле. Хорошо видно, что точки имеют систематическое смещение вверх относительно диагонали графика.
О природе переобучения
Эмпирическим риском называется средняя ошибка алгоритма на обучающей выборке. Метод минимизации эмпирического риска (empirical risk minimization, ERM) наиболее часто применяется для построения алгоритмов обучения. Он состоит в том, чтобы в рамках заданной модели выбрать алгоритм, имеющий минимальное значение средней ошибки на заданной обучающей выборке.
С переобучением метода ERM связано два утверждения, которые на первый взгляд могут показаться парадоксальными.
Утверждение 1. Минимизация эмпирического риска не гарантирует, что вероятность ошибки на тестовых данных будет мала. Легко строится контрпример — абсурдный алгоритм обучения, который минимизирует эмпирический риск до нуля, но при этом абсолютно не способен обучаться. Алгоритм состоит в следующем. Получив обучающую выборку, он запоминает её и строит функцию, которая сравнивает предъявляемый объект с запомненными обучающими объектами. Если предъявляемый объект в точности совпадает с одним из обучающих, то эта функция выдаёт для него запомненный правильный ответ. Иначе выдаётся произвольный ответ (например, случайный или всегда один и тот же). Эмпирический риск алгоритма равен нулю, однако он не восстанавливает зависимость и не обладает никакой способностью к обобщению.
Вывод: для успешного обучения необходимо не только запоминать, но и обобщать.
Утверждение 2. Переобучение появляется именно вследствие минимизации эмпирического риска. Пусть задано конечное множество из D алгоритмов, которые допускают ошибки независимо и с одинаковой вероятностью. Число ошибок любого из этих алгоритмов на заданной обучающей выборке подчиняется одному и тому же биномиальному распределению. Минимум эмпирического риска — это случайная величина, равная минимуму из D независимых одинаково распределённых биномиальных случайных величин. Её ожидаемое значение уменьшается с ростом D. Соотвественно, с ростом D увеличивается переобученность — разность вероятности ошибки и частоты ошибок на обучении.
В данном модельном примере легко построить доверительный интервал переобученности, так как функция распределения минимума известна. Однако в реальной ситуации алгоритмы имеют различные вероятности ошибок, не являются независимыми, а множество алгоритмов, из которого выбирается лучший, может быть бесконечным. По этим причинам вывод количественных оценок переобученности является сложной задачей, которой занимается теория вычислительного обучения. До сих пор остаётся открытой проблема сильной завышенности верхних оценок вероятности переобучения.
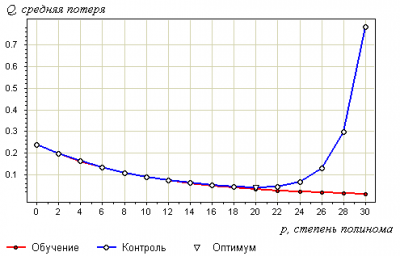
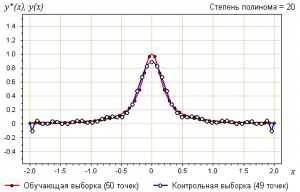
Утверждение 3. Переобучение связано с избыточной сложностью используемой модели. Всегда существует оптимальное значение сложности модели, при котором переобучение минимально.
В качестве модели рассмотрим полиномы заданной степени :
В качестве метода обучения возьмём метод наименьших квадратов:
Ниже показаны графики самой выборки и аппроксимирующей функции:
Определения
Средней потерей алгоритма на выборке называется величина
Пусть — вероятностное пространство. Ожидаемой потерей алгоритма называется величина
Не столь важно, что скрывается за термином «алгоритм». Это могут быть в частности, решающие правила в задачах классификации и распознавания образов, функции регрессии в задачах восстановления регрессии илипрогнозирования, и т. п.
Вероятность переобучения (частотное определение)
Определение. Переобученностью алгоритма относительно контрольной выборки называется разность
Определение. Вероятностью переобучения называется вероятность того, что величина переобученности превысит заданный порог :
Вероятность переобучения может быть измерена эмпирически методом Монте-Карло, см. также скользящий контроль:
Вероятность переобучения (вероятностное определение)
Определение. Переобученностью алгоритма называется разность
Определение. Вероятностью переобучения называется вероятность того, что величина переобученности превысит заданный порог :
Недостатки вероятностного определения:
Теоретические верхние оценки переобученности
Сложность
Оценки, основанные на самоограничении (self-bounding)
Оценки, основанные на последовательности выборов (microchoice bounds)
Оценки, основанные на расслоении семейства алгоритмов (shell bounds)
Разделимость
Оценки, основанные на отступах (margin-based bounds)
Устойчивость
Устойчивость алгоритма обучения (algorithmic stability)
Эмпирическое измерение переобучения
См. также
Ссылки
Overfitting — статья о переобучении в англоязычной Википедии.
Переобучение
Материал из MachineLearning.
Содержание
Обобщающая способность (generalization ability, generalization performance). Говорят, что алгоритм обучения обладает способностью к обобщению, если вероятность ошибки на тестовой выборке достаточно мала или хотя бы предсказуема, то есть не сильно отличается от ошибки на обучающей выборке. Обобщающая способность тесно связана с понятиями переобучения и недообучения.
Переобучение, переподгонка (overtraining, overfitting) — нежелательное явление, возникающее при решении задач обучения по прецедентам, когда вероятность ошибки обученного алгоритма на объектах тестовой выборки оказывается существенно выше, чем средняя ошибка на обучающей выборке. Переобучение возникает при использовании избыточно сложных моделей.
Недообучение — нежелательное явление, возникающее при решении задач обучения по прецедентам, когда алгоритм обучения не обеспечивает достаточно малой величины средней ошибки на обучающей выборке. Недообучение возникает при использовании недостаточно сложных моделей.
Пример. На рисунке справа показан эффект переобучения в одной задаче медицинского прогнозирования. Точки на графике соотвествуют различным методам обучения. Каждая точка получена путём усреднения по большому числу разбиений исходной выборки из 72 прецедентов на обучающую подвыборку и контрольную. Горизонтальная ось — частота ошибок на обучении; вертикальная — на контроле. Хорошо видно, что точки имеют систематическое смещение вверх относительно диагонали графика.
О природе переобучения
Эмпирическим риском называется средняя ошибка алгоритма на обучающей выборке. Метод минимизации эмпирического риска (empirical risk minimization, ERM) наиболее часто применяется для построения алгоритмов обучения. Он состоит в том, чтобы в рамках заданной модели выбрать алгоритм, имеющий минимальное значение средней ошибки на заданной обучающей выборке.
С переобучением метода ERM связано два утверждения, которые на первый взгляд могут показаться парадоксальными.
Утверждение 1. Минимизация эмпирического риска не гарантирует, что вероятность ошибки на тестовых данных будет мала. Легко строится контрпример — абсурдный алгоритм обучения, который минимизирует эмпирический риск до нуля, но при этом абсолютно не способен обучаться. Алгоритм состоит в следующем. Получив обучающую выборку, он запоминает её и строит функцию, которая сравнивает предъявляемый объект с запомненными обучающими объектами. Если предъявляемый объект в точности совпадает с одним из обучающих, то эта функция выдаёт для него запомненный правильный ответ. Иначе выдаётся произвольный ответ (например, случайный или всегда один и тот же). Эмпирический риск алгоритма равен нулю, однако он не восстанавливает зависимость и не обладает никакой способностью к обобщению.
Вывод: для успешного обучения необходимо не только запоминать, но и обобщать.
Утверждение 2. Переобучение появляется именно вследствие минимизации эмпирического риска. Пусть задано конечное множество из D алгоритмов, которые допускают ошибки независимо и с одинаковой вероятностью. Число ошибок любого из этих алгоритмов на заданной обучающей выборке подчиняется одному и тому же биномиальному распределению. Минимум эмпирического риска — это случайная величина, равная минимуму из D независимых одинаково распределённых биномиальных случайных величин. Её ожидаемое значение уменьшается с ростом D. Соотвественно, с ростом D увеличивается переобученность — разность вероятности ошибки и частоты ошибок на обучении.
В данном модельном примере легко построить доверительный интервал переобученности, так как функция распределения минимума известна. Однако в реальной ситуации алгоритмы имеют различные вероятности ошибок, не являются независимыми, а множество алгоритмов, из которого выбирается лучший, может быть бесконечным. По этим причинам вывод количественных оценок переобученности является сложной задачей, которой занимается теория вычислительного обучения. До сих пор остаётся открытой проблема сильной завышенности верхних оценок вероятности переобучения.
Утверждение 3. Переобучение связано с избыточной сложностью используемой модели. Всегда существует оптимальное значение сложности модели, при котором переобучение минимально.
В качестве модели рассмотрим полиномы заданной степени :
В качестве метода обучения возьмём метод наименьших квадратов:
Ниже показаны графики самой выборки и аппроксимирующей функции:


Определения
Средней потерей алгоритма на выборке называется величина
Пусть — вероятностное пространство. Ожидаемой потерей алгоритма называется величина
Не столь важно, что скрывается за термином «алгоритм». Это могут быть в частности, решающие правила в задачах классификации и распознавания образов, функции регрессии в задачах восстановления регрессии илипрогнозирования, и т. п.
Вероятность переобучения (частотное определение)
Определение. Переобученностью алгоритма относительно контрольной выборки называется разность
Определение. Вероятностью переобучения называется вероятность того, что величина переобученности превысит заданный порог :
Вероятность переобучения может быть измерена эмпирически методом Монте-Карло, см. также скользящий контроль:
Вероятность переобучения (вероятностное определение)
Определение. Переобученностью алгоритма называется разность
Определение. Вероятностью переобучения называется вероятность того, что величина переобученности превысит заданный порог :
Недостатки вероятностного определения:
Теоретические верхние оценки переобученности
Сложность
Оценки, основанные на самоограничении (self-bounding)
Оценки, основанные на последовательности выборов (microchoice bounds)
Оценки, основанные на расслоении семейства алгоритмов (shell bounds)
Разделимость
Оценки, основанные на отступах (margin-based bounds)
Устойчивость
Устойчивость алгоритма обучения (algorithmic stability)
Эмпирическое измерение переобучения
См. также
Ссылки
Overfitting — статья о переобучении в англоязычной Википедии.
Мы продолжаем знакомиться с теоретическими вопросами обучения НС, без которых невозможно их качественное построение. И это занятие начнем с очень важной темы – переобучения. Что это такое и чем это чревато? Давайте представим, что у нас есть два класса линейно-разделимых образов:
И из предыдущих занятий мы уже знаем, что для их различения достаточно одного нейрона. Но, что будет, если мы выберем сеть с большим числом нейронов, для решения этой же задачи?
В процессе обучения она способна формировать уже более сложную разделяющую линию, например, провести ее вот так:
Если мы продолжим увеличивать число нейронов скрытого слоя, то будем получать все более сложную закономерность разделения двух классов:
К чему это в итоге приведет? Да, на обучающем множестве все будет отлично, но в процессе эксплуатации такой сети будем получать массу ошибок:
Этот эффект и называется переобучением, когда разделяющая плоскость слишком точно описывает классы из обучающей выборки, и в результате теряется обобщающая способность НС.
Это можно сравнить с ленивым, но способным студентом (с прекрасной памятью), сдающим экзамен, допустим, по вышке, где предполагается решение экзаменационных задач. Ему проще выучить ход их решения не особо погружаясь в детали. Тогда, выбрав одну из них, он сможет быстренько вспомнить решение и записать его. А другой, не обладая хорошей памятью, но достаточно усидчивый, чтобы понять ход решения и запомнить их принцип, будет способен решать не только экзаменационные задачи, но и любые другие, сходные с ними. То есть, у него будет лучшая обобщающая способность.
Такой вывод может показаться несколько неожиданным. Казалось бы, чем больше нейронов в НС, тем качественнее она должна работать. Но на практике имеем обратный эффект: избыток нейронов ухудшает обобщающие способности. В идеале, число нейронов должно быть ровно столько, сколько необходимо для решения поставленной задачи. Но как определить, сколько их нужно? Здесь, опять же, нет универсального алгоритма. Это определяется опытным путем, подбирая минимальное число нейронов, при котором получается приемлемое качество решения задачи.
Рекомендация обучения №6:
Использовать минимальное необходимое число нейронов в нейронной сети.
Однако, мы все же можем контролировать этот эффект в процессе обучения. Для этого обучающая выборка разбивается на два множества: обучающее и валидации (проверочное):
На вход НС подаются наблюдения из обучающей выборки по схеме, которую мы рассматривали на предыдущем занятии. А, затем, после каждой эпохи, вычисляется критерий качества работы сети для обоих множеств: обучающего и проверочного. Получаем два графика:
Если с какой-то итерации графики начинают расходиться, то делается вывод, что НС переобучается и процесс обучения следует прервать. В этом случае, лучшие весовые коэффициенты соответствуют границе переобучения.
Здесь у вас может возникнуть вопрос: зачем мы разбиваем обучающую выборку, а не используем в качестве проверочного множества тестовое? Тестовое – это то, на котором как раз и проверяется качество работы сети:
Дело в том, что как только какая-либо выборка прямо или косвенно участвует в обучении, то она влияет на состояние весов НС. В результате выборка валидации тоже, отчасти, становится обучающей и нейросеть подстраивается и под нее. Поэтому для объективной проверки качества необходима третья выборка – тестовая. Отсюда получаем:
Рекомендация обучения №7:
Разбивать все множество наблюдений на три выборки: обучающую, валидации и тестовую.
Вот такие основные подходы существуют для предотвращения переобучения НС.
Критерии останова процесса обучения
Конечно, критерии останова могут быть и другими. Я здесь привел лишь распространенные варианты, которые чаще всего используются на практике. Но, в каждой конкретной ситуации могут быть сформулированы свои критерии останова обучения сети.
Видео по теме
Нейронные сети: краткая история триумфа
Структура и принцип работы полносвязных нейронных сетей | #1 нейросети на Python
Ускорение обучения, начальные веса, стандартизация, подготовка выборки | #4 нейросети на Python
Функции активации, критерии качества работы НС | #6 нейросети на Python
Как нейронная сеть распознает цифры | #9 нейросети на Python
Оптимизаторы в Keras, формирование выборки валидации | #10 нейросети на Python
Batch Normalization (батч-нормализация) что это такое? | #12 нейросети на Python
Как работают сверточные нейронные сети | #13 нейросети на Python
Делаем сверточную нейронную сеть в Keras | #14 нейросети на Python
Примеры архитектур сверточных сетей VGG-16 и VGG-19 | #15 нейросети на Python
Теория стилизации изображений (Neural Style Transfer) | #16 нейросети на Python
Делаем перенос стилей изображений с помощью Keras и Tensorflow | #17 нейросети на Python
Как нейронная сеть раскрашивает изображения | #18 нейросети на Python
Введение в рекуррентные нейронные сети | #19 нейросети на Python
Как рекуррентная нейронная сеть прогнозирует символы | #20 нейросети на Python
Делаем прогноз слов рекуррентной сетью Embedding слой | #21 нейросети на Python
Как работают RNN. Глубокие рекуррентные нейросети | #22 нейросети на Python
Как делать сентимент-анализ рекуррентной LSTM сетью | #24 нейросети на Python
Рекуррентные блоки GRU. Пример их реализации в задаче сентимент-анализа | #25 нейросети на Python
Двунаправленные (bidirectional) рекуррентные нейронные сети | #26 нейросети на Python
Автоэнкодеры. Что это и как работают | #27 нейросети на Python
Вариационные автоэнкодеры (VAE). Что это такое? | #28 нейросети на Python
Делаем вариационный автоэнкодер (VAE) в Keras | #29 нейросети на Python
Расширенный вариационный автоэнкодер (CVAE) | #30 нейросети на Python
Что такое генеративно-состязательные сети (GAN) | #31 нейросети на Python
Делаем генеративно-состязательную сеть в Keras и Tensorflow | #32 нейросети на Python
© 2021 Частичное или полное копирование информации с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все тексты и изображения являются собственностью сайта