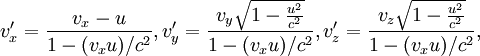что такое переносное движение твердого тела
Переносное движение
В физике, при рассмотрении нескольких систем отсчёта (СО) возникает понятие сложного движения — когда материальная точка движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом возникает вопрос о связи движений точки в этих двух СО.
Обычно выбирают одну из СО за базовую («абсолютную»), другую называют «подвижной» и вводят следующие термины:
Также вводятся понятия соответствующих скоростей и ускорений. Например, переносная скорость — это скорость точки, обусловленная движением подвижной системы отсчёта относительно абсолютной. Другими словами, это скорость точки подвижной системы отсчёта, в данный момент времени совпадающей с материальной точкой.
Оказывается, что при получении связи ускорений в разных системах отсчёта возникает необходимость ввести ещё одно ускорение, обусловленное вращением подвижной системы отсчёта:
В дальнейшем рассмотрении, базовая СО предполагается инерциальной, а на подвижную никаких ограничений не накладывается.
Содержание
Классическая механика
Кинематика сложного движения точки
Скорость
Основные задачи кинематики сложного движения заключаются в установлении зависимостей между кинематическими характеристиками абсолютного и относительного движений точки (или тела) и характеристиками движения подвижной системы отсчета, то есть переносного движения. Для точки эти зависимости являются следующими: абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей, то есть
.
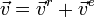
Ускорение
Связь ускорений можно найти путём дифференцирования связи для скоростей, не забывая, что координатные векторы подвижной системы координат также могут зависеть от времени.
Абсолютное ускорение точки равно геометрической сумме трёх ускорений — относительного, переносного и кориолисова, то есть
.
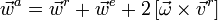
Кинематика сложного движения тела
Для твёрдого тела, когда все составные (то есть относительные и переносные) движения являются поступательными, абсолютное движение также является поступательным со скоростью, равной геометрической сумме скоростей составных движений. Если составные движения тела являются вращательными вокруг осей, пересекающихся в одной точке (как, например, у гироскопа), то результирующее движение также является вращательным вокруг этой точки с мгновенной угловой скоростью, равной геометрической сумме угловых скоростей составных движений. Если же составными движениями тела являются и поступательные, и вращательные, то результирующее движение в общем случае будет слагаться из серии мгновенных винтовых движений.
Рассчитать взаимосвязь скоростей разных точек твёрдого тела в разных системах отсчёта можно с помощью комбинирования формулы сложения скоростей и формулы Эйлера для связи скоростей точек твёрдого тела. Связь ускорений находится простым дифференцированием полученного векторного равенства по времени.
Динамика сложного движения точки
При рассмотрении движения в неинерциальной СО нарушаются первые 2 закона Ньютона. Чтобы обеспечить формальное их выполнение, обычно вводятся дополнительные, фиктивные (не существующие на самом деле), силы инерции: центробежная сила и сила Кориолиса. Выражения для этих сил получаются из связи ускорений (предыдущий раздел).
Релятивистская механика
Скорость
При скоростях, близких к скорости света, преобразования Галилея не являются точно инвариантными и классическая формула сложения скоростей перестаёт выполняться. Вместо этого, инвариантными являются преобразования Лоренца, а связь скоростей в двух инерциальных СО получается следующей: 
в предположении, что скорость 
направлена вдоль оси х системы S. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.
Однако вводится величина — быстрота — которая аддитивна при переходе от одной СО к другой.
Неинерциальные СО
Связь скоростей и ускорений в системах отсчёта, движущихся друг относительно друга ускоренно, является значительно более сложной и определяется локальными свойствами пространства в рассматриваемых точках (зависит от производной тензора Римана).
Литература
См. также
Ссылки
Полезное
Смотреть что такое «Переносное движение» в других словарях:
ПЕРЕНОСНОЕ ДВИЖЕНИЕ — в механике, движение подвижной системы отсчёта по отношению к системе отсчёта, принятой за основную (условно считаемую неподвижной). (см. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ). Физический энциклопедический словарь. М.: Советская энциклопедия. Главный редактор… … Физическая энциклопедия
ПЕРЕНОСНОЕ ДВИЖЕНИЕ — перемещение подвижной системы отсчёта (напр. движение вагона с передвигающимся в нём человеком), по отношению к которой точка, тело (человек) совершает относительное (см.) … Большая политехническая энциклопедия
ПЕРЕНОСНОЕ ДВИЖЕНИЕ — перемещение подвижной системы отсчета, по отношению к которой точка или тело совершает относительное движение … Большой Энциклопедический словарь
переносное движение — Движение подвижной системы отсчета по отношению к основной системе отсчета. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно технической терминологии. 1984 г.] Тематики теоретическая механика … Справочник технического переводчика
переносное движение — 3.29 переносное движение : Совместное движение сооружения и основания во время землетрясения как единого недеформируемого целого с ускорениями (скоростями или смещениями) основания. Источник: СП 14.13330.2014: Строительство в сейсмических районах … Словарь-справочник терминов нормативно-технической документации
переносное движение — движение подвижной системы отсчёта по отношению к системе отсчёта, принятой за основную (условно считаемую неподвижной). * * * ПЕРЕНОСНОЕ ДВИЖЕНИЕ ПЕРЕНОСНОЕ ДВИЖЕНИЕ, перемещение подвижной системы отсчета, по отношению к которой точка или тело… … Энциклопедический словарь
переносное движение — nešamasis judėjimas statusas T sritis fizika atitikmenys: angl. bulk motion vok. Führungsbewegung, f rus. переносное движение, n pranc. mouvement d’entraînement, m; mouvement translatif, m … Fizikos terminų žodynas
ПЕРЕНОСНОЕ ДВИЖЕНИЕ — движение подвижной системы отсчёта по отношению к т. н. абсолютной (обычно инерциальной) системе отсчёта (см. Относительное движение) … Большой энциклопедический политехнический словарь
ПЕРЕНОСНОЕ ДВИЖЕНИЕ — движение подвижной системы отсчёта по отношению к системе отсчёта, принятой за основную (условно считаемую неподвижной) … Естествознание. Энциклопедический словарь
переносное движение — Движение подвижной системы отсчёта по отношению к основной системе отсчёта … Политехнический терминологический толковый словарь
Переносная скорость
В физике, при рассмотрении нескольких систем отсчёта (СО) возникает понятие сложного движения — когда материальная точка движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом возникает вопрос о связи движений точки в этих двух СО.
Обычно выбирают одну из СО за базовую («абсолютную»), другую называют «подвижной» и вводят следующие термины:
Также вводятся понятия соответствующих скоростей и ускорений. Например, переносная скорость — это скорость точки, обусловленная движением подвижной системы отсчёта относительно абсолютной. Другими словами, это скорость точки подвижной системы отсчёта, в данный момент времени совпадающей с материальной точкой.
Оказывается, что при получении связи ускорений в разных системах отсчёта возникает необходимость ввести ещё одно ускорение, обусловленное вращением подвижной системы отсчёта:
В дальнейшем рассмотрении, базовая СО предполагается инерциальной, а на подвижную никаких ограничений не накладывается.
Содержание
Классическая механика
Кинематика сложного движения точки
Скорость
Основные задачи кинематики сложного движения заключаются в установлении зависимостей между кинематическими характеристиками абсолютного и относительного движений точки (или тела) и характеристиками движения подвижной системы отсчета, то есть переносного движения. Для точки эти зависимости являются следующими: абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей, то есть
.
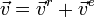
Ускорение
Связь ускорений можно найти путём дифференцирования связи для скоростей, не забывая, что координатные векторы подвижной системы координат также могут зависеть от времени.
Абсолютное ускорение точки равно геометрической сумме трёх ускорений — относительного, переносного и кориолисова, то есть
.
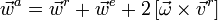
Кинематика сложного движения тела
Для твёрдого тела, когда все составные (то есть относительные и переносные) движения являются поступательными, абсолютное движение также является поступательным со скоростью, равной геометрической сумме скоростей составных движений. Если составные движения тела являются вращательными вокруг осей, пересекающихся в одной точке (как, например, у гироскопа), то результирующее движение также является вращательным вокруг этой точки с мгновенной угловой скоростью, равной геометрической сумме угловых скоростей составных движений. Если же составными движениями тела являются и поступательные, и вращательные, то результирующее движение в общем случае будет слагаться из серии мгновенных винтовых движений.
Рассчитать взаимосвязь скоростей разных точек твёрдого тела в разных системах отсчёта можно с помощью комбинирования формулы сложения скоростей и формулы Эйлера для связи скоростей точек твёрдого тела. Связь ускорений находится простым дифференцированием полученного векторного равенства по времени.
Динамика сложного движения точки
При рассмотрении движения в неинерциальной СО нарушаются первые 2 закона Ньютона. Чтобы обеспечить формальное их выполнение, обычно вводятся дополнительные, фиктивные (не существующие на самом деле), силы инерции: центробежная сила и сила Кориолиса. Выражения для этих сил получаются из связи ускорений (предыдущий раздел).
Релятивистская механика
Скорость
При скоростях, близких к скорости света, преобразования Галилея не являются точно инвариантными и классическая формула сложения скоростей перестаёт выполняться. Вместо этого, инвариантными являются преобразования Лоренца, а связь скоростей в двух инерциальных СО получается следующей:
в предположении, что скорость направлена вдоль оси х системы S. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.
Однако вводится величина — быстрота — которая аддитивна при переходе от одной СО к другой.
Неинерциальные СО
Связь скоростей и ускорений в системах отсчёта, движущихся друг относительно друга ускоренно, является значительно более сложной и определяется локальными свойствами пространства в рассматриваемых точках (зависит от производной тензора Римана).
Литература
См. также
Ссылки
Полезное
Смотреть что такое «Переносная скорость» в других словарях:
переносная скорость — nešimo greitis statusas T sritis fizika atitikmenys: angl. reference frame velocity; velocity of moving space vok. Führungsgeschwindigkeit, f rus. переносная скорость, f pranc. vitesse d’entraînement, f … Fizikos terminų žodynas
переносная скорость точки — При сложном движении точки — скорость той, неизменно связанной с подвижной системой отсчета точки пространства, с которой в данный момент времени совпадает движущаяся точка. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая… … Справочник технического переводчика
переносная скорость точки — При сложном движении точки скорость той, неизменно связанной с подвижной системой отсчёта точки пространства, с которой в данный момент времени совпадает движущаяся точка … Политехнический терминологический толковый словарь
Абсолютная, относительная и переносная скорости — В физике, при рассмотрении нескольких систем отсчёта (СО) возникает понятие сложного движения когда материальная точка движется относительно какой либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом … Википедия
Абсолютная скорость — В физике, при рассмотрении нескольких систем отсчёта (СО) возникает понятие сложного движения когда материальная точка движется относительно какой либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом … Википедия
Относительная скорость — В физике, при рассмотрении нескольких систем отсчёта (СО) возникает понятие сложного движения когда материальная точка движется относительно какой либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом … Википедия
Лопастной компрессор — Лопаточный, лопастной компрессор это разновидность компрессоров, предназначенная для повышения давления рабочего тела за счёт взаимодействия последнего с подвижными и неподвижными лопаточными решётками компрессора. Принцип действия… … Википедия
Лопаточный компрессор — Лопаточный или лопастной компрессор это разновидность компрессоров, предназначенная для повышения давления рабочего тела за счёт взаимодействия последнего с подвижными и неподвижными лопаточными решётками компрессора. Принцип действия лопаточных… … Википедия
Осевой компрессор — Лопаточный или лопастной компрессор это разновидность компрессоров, предназначенная для повышения давления рабочего тела за счёт взаимодействия последнего с подвижными и неподвижными лопаточными решётками компрессора. Принцип действия лопаточных… … Википедия
Переносное ускорение
В физике, при рассмотрении нескольких систем отсчёта (СО) возникает понятие сложного движения — когда материальная точка движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом возникает вопрос о связи движений точки в этих двух СО.
Обычно выбирают одну из СО за базовую («абсолютную»), другую называют «подвижной» и вводят следующие термины:
Также вводятся понятия соответствующих скоростей и ускорений. Например, переносная скорость — это скорость точки, обусловленная движением подвижной системы отсчёта относительно абсолютной. Другими словами, это скорость точки подвижной системы отсчёта, в данный момент времени совпадающей с материальной точкой.
Оказывается, что при получении связи ускорений в разных системах отсчёта возникает необходимость ввести ещё одно ускорение, обусловленное вращением подвижной системы отсчёта:
В дальнейшем рассмотрении, базовая СО предполагается инерциальной, а на подвижную никаких ограничений не накладывается.
Содержание
Классическая механика
Кинематика сложного движения точки
Скорость
Основные задачи кинематики сложного движения заключаются в установлении зависимостей между кинематическими характеристиками абсолютного и относительного движений точки (или тела) и характеристиками движения подвижной системы отсчета, то есть переносного движения. Для точки эти зависимости являются следующими: абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей, то есть
.
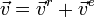
Ускорение
Связь ускорений можно найти путём дифференцирования связи для скоростей, не забывая, что координатные векторы подвижной системы координат также могут зависеть от времени.
Абсолютное ускорение точки равно геометрической сумме трёх ускорений — относительного, переносного и кориолисова, то есть
.
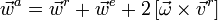
Кинематика сложного движения тела
Для твёрдого тела, когда все составные (то есть относительные и переносные) движения являются поступательными, абсолютное движение также является поступательным со скоростью, равной геометрической сумме скоростей составных движений. Если составные движения тела являются вращательными вокруг осей, пересекающихся в одной точке (как, например, у гироскопа), то результирующее движение также является вращательным вокруг этой точки с мгновенной угловой скоростью, равной геометрической сумме угловых скоростей составных движений. Если же составными движениями тела являются и поступательные, и вращательные, то результирующее движение в общем случае будет слагаться из серии мгновенных винтовых движений.
Рассчитать взаимосвязь скоростей разных точек твёрдого тела в разных системах отсчёта можно с помощью комбинирования формулы сложения скоростей и формулы Эйлера для связи скоростей точек твёрдого тела. Связь ускорений находится простым дифференцированием полученного векторного равенства по времени.
Динамика сложного движения точки
При рассмотрении движения в неинерциальной СО нарушаются первые 2 закона Ньютона. Чтобы обеспечить формальное их выполнение, обычно вводятся дополнительные, фиктивные (не существующие на самом деле), силы инерции: центробежная сила и сила Кориолиса. Выражения для этих сил получаются из связи ускорений (предыдущий раздел).
Релятивистская механика
Скорость
При скоростях, близких к скорости света, преобразования Галилея не являются точно инвариантными и классическая формула сложения скоростей перестаёт выполняться. Вместо этого, инвариантными являются преобразования Лоренца, а связь скоростей в двух инерциальных СО получается следующей:
в предположении, что скорость направлена вдоль оси х системы S. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.
Однако вводится величина — быстрота — которая аддитивна при переходе от одной СО к другой.
Неинерциальные СО
Связь скоростей и ускорений в системах отсчёта, движущихся друг относительно друга ускоренно, является значительно более сложной и определяется локальными свойствами пространства в рассматриваемых точках (зависит от производной тензора Римана).
Литература
См. также
Ссылки
Полезное
Смотреть что такое «Переносное ускорение» в других словарях:
переносное ускорение — nešimo pagreitis statusas T sritis fizika atitikmenys: angl. acceleration of transport; acceleration of transportation; drag acceleration vok. Führungsbeschleunigung, f rus. переносное ускорение, n pranc. accélération d’entraînement, f … Fizikos terminų žodynas
переносное ускорение точки — При сложном движении точки — ускорение той, неизменно связанной с подвижной системой отсчета точки пространства, с которой в данный момент времени совпадает движущаяся точка. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая… … Справочник технического переводчика
переносное ускорение точки — При сложном движении точки ускорение той, неизменно связанной с подвижной системой отсчёта точки пространства, с которой в данный момент времени совпадает движущаяся точка … Политехнический терминологический толковый словарь
УСКОРЕНИЕ — (1) материальной точки векторная величина а, характеризующая быстроту изменения с течением времени вектора скорости v (см. (1)) точки: Согласно второму закону Ньютона (см.), ускорение прямо пропорционально результирующей механической силе F,… … Большая политехническая энциклопедия
Переносное движение — В физике, при рассмотрении нескольких систем отсчёта (СО) возникает понятие сложного движения когда материальная точка движется относительно какой либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом … Википедия
КОРИОЛИСА УСКОРЕНИЕ — (поворотное ускорение), составляющая полного ускорения точки, к рая появляется при т. н. сложном движении (см. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ), когда переносное движение, т … Физическая энциклопедия
Абсолютное, относительное и переносное ускорения — В физике, при рассмотрении нескольких систем отсчёта (СО) возникает понятие сложного движения когда материальная точка движется относительно какой либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом … Википедия
Абсолютное относительное и переносное ускорения — В физике, при рассмотрении нескольких систем отсчёта (СО) возникает понятие сложного движения когда материальная точка движется относительно какой либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом … Википедия
Относительное и переносное ускорения Абсолютное — В физике, при рассмотрении нескольких систем отсчёта (СО) возникает понятие сложного движения когда материальная точка движется относительно какой либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом … Википедия
Абсолютное ускорение — В физике, при рассмотрении нескольких систем отсчёта (СО) возникает понятие сложного движения когда материальная точка движется относительно какой либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом … Википедия
iSopromat.ru
Сложным называют движение точки по отношению к двум или нескольким системам отсчета.
Законы Ньютона сформулированы для движения точки по отношению к инерциальным системам отсчета. Для определения кинематических параметров точки при движении относительно произвольно движущейся системы отсчета вводится теория сложного движения.
На рисунке 3.1 показаны:
Движение точки M в данном случае является сложным. Её движение по отношению к подвижной системе отсчета называют относительным движением.
Движение той точки подвижной системы отсчета, в которой в данный момент находится движущаяся точка, по отношению к неподвижной системе отсчета называют переносным движением. Движение точки M по отношению к неподвижной системе отсчета называют абсолютным движением.
Ниже приведен пример сложного движения точки — M.
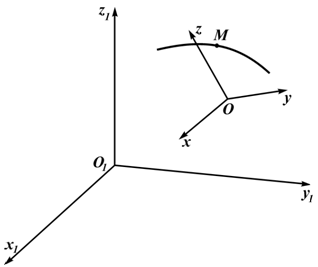
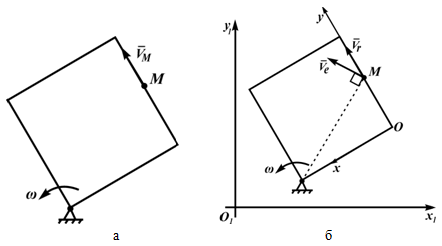
На рисунке 3.2,а показан квадрат, вращающийся в плоскости чертежа вокруг неподвижной точки. По стороне квадрата движется точка M. Она участвует в двух движениях, поэтому можно ввести две системы отсчета: неподвижную, например, O1x1y1z1 — по отношению к которой вращается квадрат и подвижную Oxyz, скрепленную с квадратом, по оси Oy которой движется точка M (рисунок 3.2,б).
Движение точки M по стороне квадрата (по оси Oy скрепленной с квадратом подвижной системы) является относительным — скорость в этом движении Vr.
Вращение точки M вместе с квадратом — переносное движение, скорость в этом движении — Ve. Абсолютное движение является результатом сложения переносного и относительного движений.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах