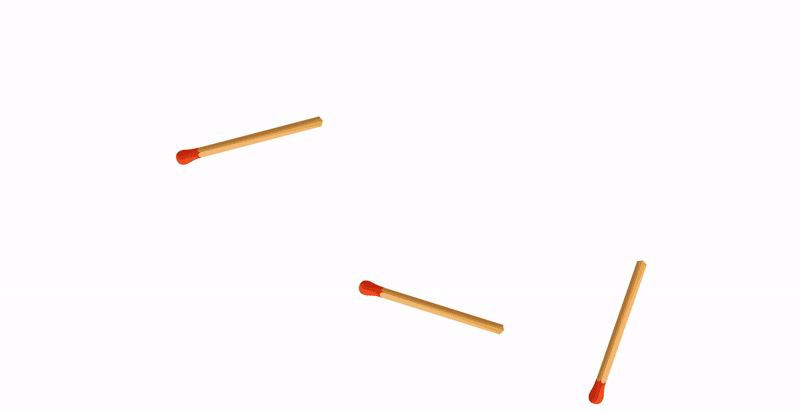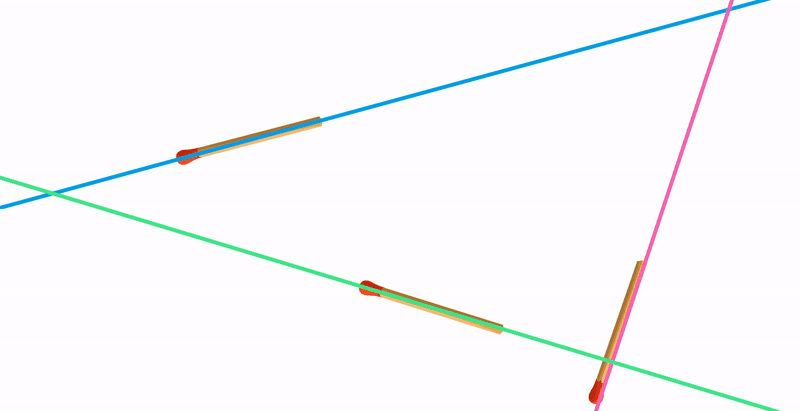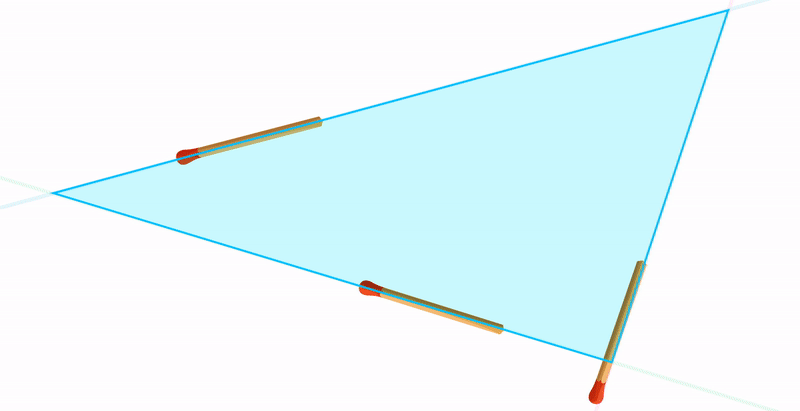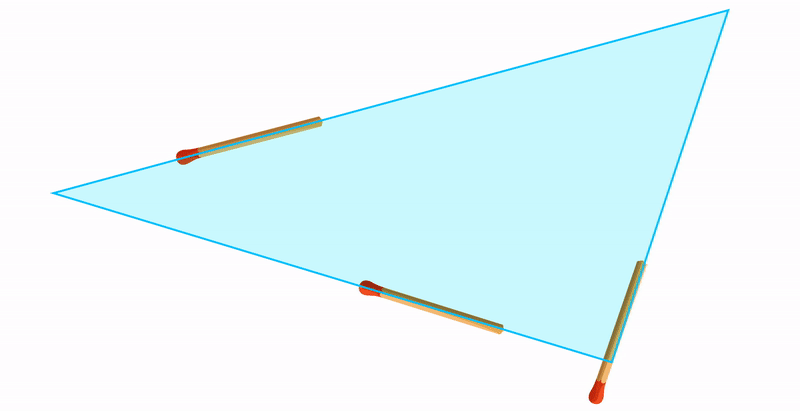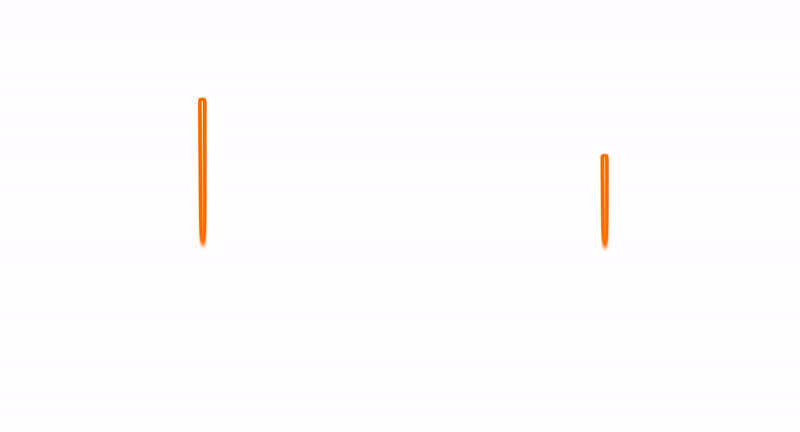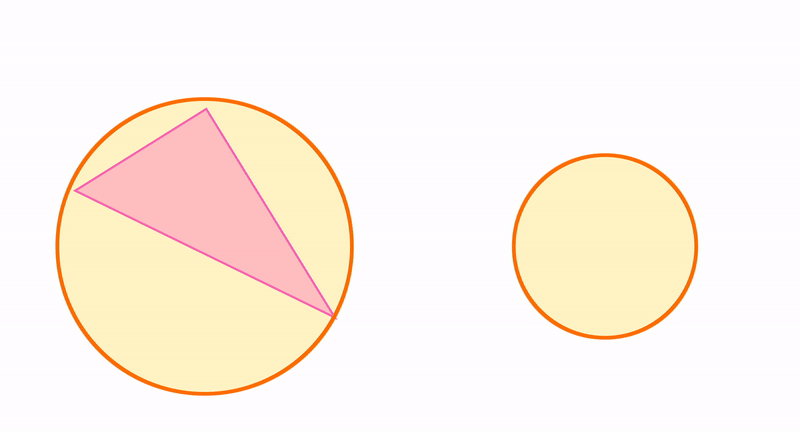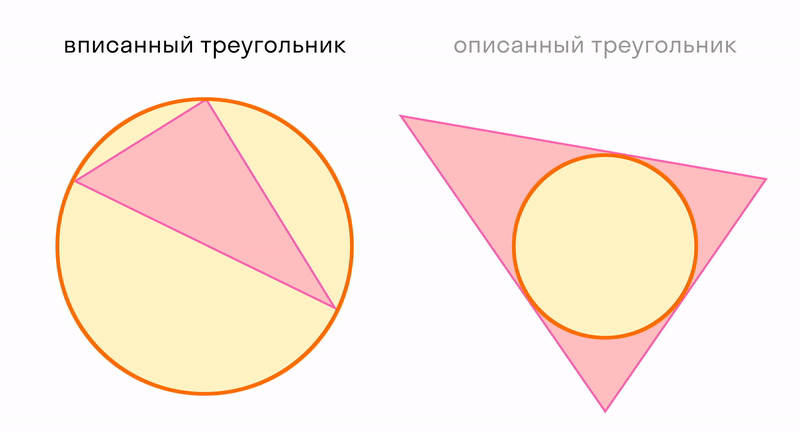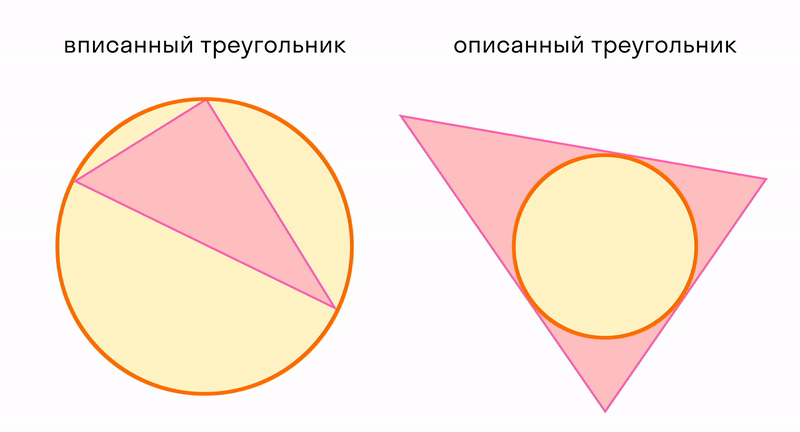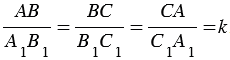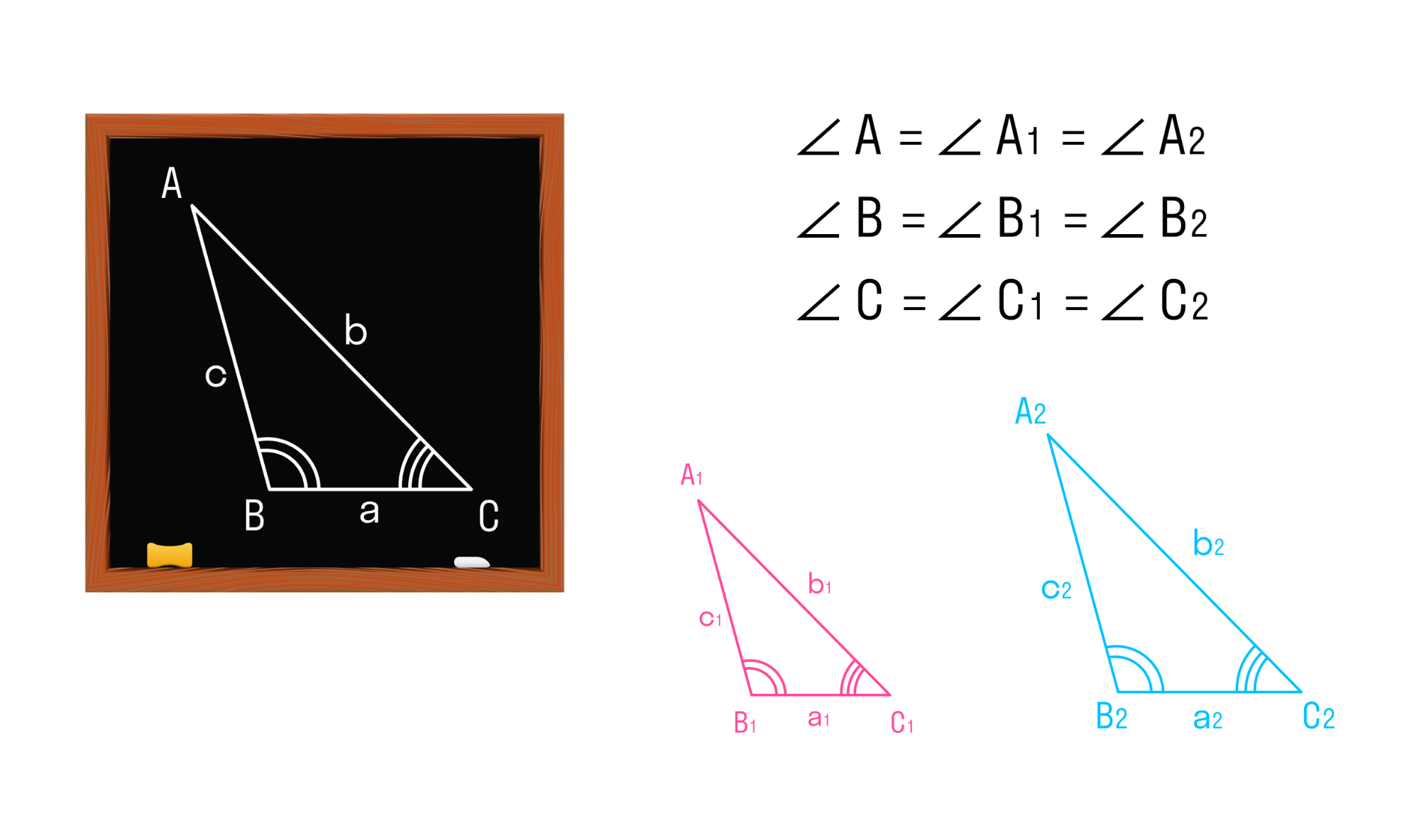что такое основание в геометрии определение
Основание в математике
Смотреть что такое «Основание в математике» в других словарях:
ОСНОВАНИЕ — • ОСНОВАНИЕ, в геометрии сторона треугольника, противолежащая углу, от вершины которого проводится высота. • ОСНОВАНИЕ, в математике число единиц в системе счисления, равное одной единице следующего, более высокого, разряда этой системы.… … Научно-технический энциклопедический словарь
ОСНОВАНИЕ — достаточное условие для чего либо: бытия, познания, мысли, деятельности. Напр., О. материальных явлений это их причины; О. поступков их мотивы; О. суждений др. суждения (посылки) или опыт. Разыскание О. наз. обоснованием; обосновать… … Философская энциклопедия
ОСНОВАНИЕ — ОСНОВАНИЕ, я, ср. 1. см. основать, ся. 2. Опорная часть предмета, сооружения, основа (в 1 знач.). Дом на каменном основании. 3. В математике: сторона геометрической фигуры или грань геометрического тела, перпендикулярная высоте. О. треугольника,… … Толковый словарь Ожегова
Конкретная математика. Основание информатики — Обложка «Конкретная математика. Основание информатики» книга Дональда Кнута, Роналда Грэхема и Орена Паташника по математике, рассматривающая математические основы информатики, особенно анализа алгоритмов. Вынесеный в заглавие книги термин… … Википедия
Сравнение в математике — Говорят, что a сравнимо с b по модулю n, если a b делится на n. Это обозначают так: a ≡ b (mod n). С. имеют много сходства с равенствами. Если f(x) целая функция с целыми коэффициентами и а ≡ b (mod n), то f(a) ≡ f(b) (mod n). Решить С. f(x) ≡ 0… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Сравнение, в математике — Говорят, что a сравнимо с b по модулю n, если a b делится на n. Это обозначают так: a ≡ b (mod n). С. имеют много сходства с равенствами. Если f(x) целая функция с целыми коэффициентами и а ≡ b (mod n), то f(a) ≡ f(b) (mod n). Решить С. f(x) ≡ 0… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Логарифм — График двоичного логарифма Логарифм числа … Википедия
КОГЕН — (Cohen) Герман (1842 1918) немецкий философ, основатель и виднейший представитель марбургской школы неокантианства. Основные работы: ‘Теория опыта Канта’ (1885), ‘Обоснование Кантом этики’ (1877), ‘Обоснование Кантом эстетики’ (1889), ‘Логика… … История Философии: Энциклопедия
ЛЕЙБНИЦ — (Leibniz) Готфрид Вильгельм (1646 1716) нем. философ, математик, физик и изобретатель, юрист, историк, языковед. Изучал юриспруденцию и философию в Лейпцигском и Йенском ун тах. В 1672 1676 в Париже. С 1676 состоял на службе у ганноверских… … Философская энциклопедия
Фибоначчи — (Fibonacci) Фибоначчи первый крупный математик средневековой Европы Десятичная система счисления, арабские цифры, числа, последовательность, уровни, ряд, линии и спираль Фибоначчи Содержание >>>>>>>>> … Энциклопедия инвестора
ОСНОВАНИЯ ГЕОМЕТРИИ
раздел геометрии, в к-ром исследуются основные понятия геометрии, соотношения между ними и связанные с ними вопросы.
Важная роль основных понятий и соотношений между ними, на базе к-рых строятся определения фигур и доказываются геометрич. предложения, отмечается уже в работах античных геометров. Так, развивая дедуктивный метод в геометрии, они указывали на особую роль основных понятий, аксиом и постулатов, составляющих фундамент геометрии. В «Началах» Евклида (3 в. до н. э.) аксиомам и постулатам предпослана цепь определений всех понятий, к-рые используются в дальнейшем изложении. Среди этих определений особое место принадлежит понятиям «точка», «прямая», «плоскость», определения к-рых не опираются на другие геометрич. понятия. Сами определения этих основных понятий с геометрич. точки зрения неудовлетворительны, т. к. они выражают лишь характерное физич. свойство (напр., «точка есть то, что не имеет частей», т. е. под точкой понимается малое физически неделимое тело). Поэтому уже в трудах геометров, написанных почти одновременно с «Началами», содержатся многочисленные комментарии и критич. анализ определений основных и других геометрич. понятий, аксиом и постулатов. Но это были лишь уточнения, не затрагивающие основы определений. По существу, доказательства многих гоометрич. теорем опирались в основном на наглядность чертежа, на физич. осуществимость необходимых геометрич. построений, а не выводились строго логически из аксиом и постулатов. Только в 19 в. и особенно в нач. 20 в. появляются работы, в к-рых выясняется все глубокое значение основных понятий и соотношений между ними для логически безупречного дедуктивного метода построения геометрии и ее обоснования. Причем во многом этому углубленному анализу основ геометрии способствовало открытие неевклидовой геометрии Лобачевского (1826). Результаты по обоснованию евклидовой геометрии на основе тех же принципов и понятий, что и в «Началах» Евклида, содержатся в работах Дж. Пеано (G. Реапо, 1894), М. Паша (М. Pasch, 1882), М. Пиери (М. Pieri, 1899), Д. Гильберта (D. Hilbert) и др. Наибольшую известность получила Гильберта система аксиом евклидовой геометрии (1899). Добиваясь логически удовлетворительного построения евклидовой геометрии, Д. Гильберт выделил 5 групп аксиом, показал их необходимость и достаточность для построения всей евклидовой геометрии. Вместе с тем впервые была проведена логич. обработка всей системы, выяснена непротиворечивость системы с помощью построения числовой модели, установлена независимость групп аксиом, а также полнота системы. В отличие от концепции пространства как «места» для всех фигур, проводимой в «Началах», Д. Гильберт рассматривает его как множество всех «точек», «прямых», «плоскостей» и фигур, построенных на основе этих понятий.
Набор основных понятий в системе Гильберта был заимствован (и уточнен) из «Начал», однако эта система является, по существу, чисто геометрич. схемой, свободной от ссылок на наглядность чертежа. Вместе с тем язык геометрии, построенной на основе системы Гильберта, почти не отличается от языка «Начал».
Почти одновременно с системой Гильберта появились и др. системы аксиом евклидовой геометрии. Так, в системе Ф. Шура (F. Schur, 1909) в качестве основных понятий были «точка», «отрезок» и т. д., а вместо «конгруэнтности» фигур в этой системе вводилось понятие «движение». Введение понятия «движение» позволило применить в геометрии групповой подход к исследованию движений, алгебраизировать методы исследования. Упомянутые выше геометрич. схемы не полностью удовлетворяют требованиям дальнейшего обобщения понятия пространства и др. понятий и, кроме того, недостаточно «алгебраичны».
Новые подходы к обоснованию евклидовой геометрии потребовали выработки нового «языка», с помощью к-рого оказывается возможным провести соответствующие дальнейшие обобщения понятий, алгебраизацию доказательств, классификацию объектов и т. д. Одной из распространенных схем основания евклидовой геометрии, в к-рой сконцентрированы возможности обобщений, перевода на язык алгебры геометрич. понятий, является система аксиом, предложенная Г. Вейлем (Н. Weil, 1916). Ниже приводится одна из транскрипций схемы Вейля.
На основе этой группы аксиом определяется сумма векторов, к-рая удовлетворяет требованиям коммутативности и ассоциативности. Существует нуль-вектор, противоположный вектор. Векторы по сложению образуют группу.
С помощью операций сложения и умножения на число определяется линейная комбинация векторов, их линейная зависимость.
Эта аксиома имеет топологич. характер; из нее вместе со второй группой аксиом следует, что R 3 является топологич. пространством размерности 3. Первые три группы аксиом определяют трехмерное аффинное пространство.
Схема Вейля допускает обобщение на случай любой размерности, с помощью соответствующего изменения аксиом в эту схему включаются гиперболич. и эллиптич. пространства и т. д.
В качестве основных понятий при создании схемы евклидовой геометрии могут быть положены геометрич. преобразования. Так, в системе аксиом Ф. Бахмана (P. Bachmann) в качестве такого понятия вводится преобразование симметрии. С помощью симметрии, порождающих группу движений евклидовой (метрической) плоскости, определяются «точки» и «прямые» как инволютивные элементы этой группы. Теоретико-групповые отношения являются основой при определении понятий «инцидентность», «ортогональность» и т. п., геометрич. доказательства заменяются вычислениями, переводятся на язык алгебры.
Групповой подход впервые был четко сформулирован в эрлангенской программе Ф. Клейна: геометрич. пространство определяется как множество Ф с фиксированной группой Wего преобразований; объектом геометрии является изучение W-инвариантных свойств пространства. (Напр., n-мерное аффинное пространство А n определяется как множество, на к-ром просто транзитивно действует векторная группа размерности п.) С. Ли, Ф. Клейн, А. Кэли провели исследование групп преобразований, на основе к-рого возникают новые возможности в классификации и обосновании евклидовой и неевклидовых геометрий как геометрий определенных групп преобразований. Геометрия становится учением об инвариантах групп преобразований, и О. г. опирается на теорию групп.
В работах Б. Римана был разработан метрич. подход к О. г. Геометрич. пространство рассматривается как множество, снабженное метрикой, к-рая удовлетворяет тем или иным аксиомам. Б. Риман показал, что все внутренние свойства пространства определяются заданной квадратичной дифференциальной формой (кривизна, геодезич. линии и т. д.), тем самым были открыты широкие классы различных метрич. геометрий. Впервые классификация пространств и их геометрий была осуществлена на метрич. основе. Б. Риман указал на особую роль выбора координат в точечном многообразии для исследования самих квадратичных форм. Так, для пространства постоянной римановой кривизны Б. Риман привел стандартный вид, к к-рому может быть приведена квадратичная форма путем соответствующего выбора координат.
Координатный метод евклидовой геометрии был обобщен для различных пространств, а также нашел развитие в дифференциальной геометрии; понятие многообразий, опирающееся на выбор координатных систем, получает многочисленные применения в геометрии. Групповой подход к исследованию преобразований дифференциально-геометрич. объектов позволил создать теорию инвариантов метрических (квадратичных) форм. Эта теория инвариантов групп преобразований явилась основой для построения и логич. обоснования современной дифференциальной геометрии. В качестве одного из основных понятий выкристаллизовалось понятие геометрич. объекта, геометрия рассматривается как геометрических объектов теория. Понятие дифференцируемого многообразия позволяет дать строгие определения дифференциально-геометрич. объектам, в частности обосновать методы анализа в геометрии и геометрич. методы в анализе.
Обоснование евклидовой (и, вообще, любой) геометрии, опирающееся на определенную систему аксиом, обнаруживает особую роль теоретико-множественных принципов при логич. анализе систем аксиом. Именно, независимость и непротиворечивость системы аксиом может быть установлена путем построения числовой модели, реализующей эту систему. Поэтому теория множеств в О. г. является своего рода эталоном безупречного логич. построения геометрич. теории. Геометрич. аксиомы непрерывности (и полноты) по существу являются нек-рыми эквивалентами теоретико-множественных аксиом.
Построение геометрии над определенным полем обосновывается путем применения понятий теоретико-множественного характера. Начиная с создания декартовой аналитич. еометрии, идея отображения множества точек на множество действительных чисел (или на произвольное числовое множество) приобретает большое значение для О. г. Развитие этой идеи позволяет определить и классифицировать геометрии по тому числовому множеств, над к-рым они построены.
В О. г. широко применяются теоретико-множественные методы для изучения геометрич. преобразований. Как уже отмечалось выше, инварианты групп преобразований являются предметом изучения в определенной этой группой геометрии. Важное применение теории инвариантов (проективных) преобразований нашел Ф. Клейн для интерпретации неевклидовых пространств и доказательства непротиворечивости неевклидовых геометрий. Углубленному анализу подверглись такие понятия, как «угол», «ортогональность» и т. д. Исследования проективных комплексных пространств, различных проективных мероопределений имеют большое значение в классификации пространств с определенной структурой.
В О. г. применяются также топологич. методы классификации многообразий, с помощью этих методов выявляются наиболее существенные различия между классами и типами многообразий, исследуются глобальные их свойства.
Изучение средств, используемых в доказательствах теорем на основе данной системы аксиом, является одной из важных проблем в О. г. В «Началах» Евклида для доказательств применялась классич. логика Аристотеля. Много внимания уделил этим вопросам Д. Гильберт, наметивший основные задачи математич. логики. Непротиворечивость систем геометрич. аксиом устанавливается путем построения числовых моделей этих систем и их логического исследования.
Значительное место в О. г. занимают вопросы измерения отрезков, площадей, объемов. Понятия меры отрезка, площади, объема основываются на определенных группах аксиом. Так, напр., теория площадей многоугольников на евклидовой плоскости в системе аксиом Гильберта обосновывается аксиомами, относящимися только к плоскости и независимо от аксиом непрерывности (см. Неархимедова геометрия, Непаскалева геометрия).
В О. г. исследуется проблема о материальных объективных истоках геометрич. понятии и систем аксиом. Одним из принципов построения геометрич. систем долгое время являлся принцип физич. осуществимости системы на какой-либо материальной модели. Как отмечалось выше, еще в «Началах» была сделана попытка дать истолкование основных понятии с точки зрения их физич. свойств. В кон. 19 в., после открытия геометрии Лобачевского, вновь возник вопрос об объективной возможности других, отличных от евклидовой, геометрий. Проблему объективного существования неевклидовых геометрий многие геометры решали путем построения физич. моделей, с помощью к-рых пытались убедиться в независимости и непротиворечивости геометрич. систем аксиом. Так, Н. И. Лобачевский пытался обосновать непротиворечивость выводов, вытекающих из его аксиомы о параллельных, путем физич. измерений дефектов треугольников гигантских размеров, вершины к-рых располагались на удаленных от Земли космич. телах, чтобы убедиться в том, что дефекты различны для различных треугольников и что сумма внутренних углов треугольников может быть меньше двух прямых углов. Попытку обосновать существование различных метрич. геометрий предпринял Г. Гельмгольц (Н. Helmholtz). и работе, написанной вскоре после появления результатов Б. Римана. Основным понятиям, к-рыми оперирует метрич. геометрия, Г. Гельмгольц дал физич. истолкование, в основу геометрич. свойств пространства он положил нек-рые физич. законы, из к-рых вытекает возможность построения геометрии этого пространства. Эвристическим путем из основных физич. законов Г. Гельмгольц получил метрику пространства в виде дифференциальной формы, к-рая, как показал Б. Риман, определяет все внутренние свойства пространства. Вместо гипотез, лежащих в О. г., предложенных Б. Риманом, Г. Гельмгольц рассматривал факты, из к-рых вытекали те же выводы в метрич. геометрии, подчеркивая тем самым опытную проверку справедливости (непротиворечивости) этих выводов.
Объективно работы по опытной проверке геометрич. систем служили распространению новых геометрич. идей, способствовали появлению углубленного логич. анализа геометрич. систем, выработке современных основных требований к этим системам. Вместе с тем попытки физич. обоснования геометрии способствовали проникновению геометрических идей и методов в различные области математики, физики и механики.
О. г. имеют большое значение в методологии геометрии. В процессе преподавания современных курсов геометрии в университетах и педагогич. вузах раздел О. г. занимает одно из центральных мест. В связи с этим все большую роль играет выбор системы основных понятий и аксиом, чтобы «сократить» путь от самих аксиом до выводимых из них содержательных теорем, находящих практич. применение (в частности, в решении задач).
Лит.:[1] Начала Евклида, кн. 1-15, пер. с греч., М., 1948-50; [2] Гильберт Д., Основания геометрии, пер. с нем., М.-Л., 1948; [3] Веблен О., Уайтхед Д ж., Основании дифференциальной геометрии, пер. с англ., М., 1949; [4] Об основаниях геометрии, М., 1956; [5] Каган В. Ф., Основания геометрии, ч. 1-2, М.- Л., 1949-56; [6] Каган В. Ф., Очерки по геометрии, М., 1903; [7] Буземан Г., Геометрия геодезических, пер. с англ., М., 1962; [8] Ефимов Н. В., Высшая геометрия, 6 изд., М., 1978; [9] Бахнан Ф., Построение геометрии на основе понятия симметрии, пер. с нем., М., 1969; [10] Р о з е н ф е л ь д Б. А., Истории неевклидовой геометрии, М., 1976; [11] II о г о р е л о н А. В., Элементарная геометрия, 2 над., М., 1974; [12] Шоке Г., Геометрия, пер. с франц., М., 1970; [13] Д о н е д д ю А., Евклидова планиметрия, пер. с франц., М., 1978; [14] К а р т е с и Ф., Введение в конечные геометрии, пер. с англ., М., 1980.
Равнобедренный треугольник: свойства, признаки и формулы
Определение равнобедренного треугольника
Какой треугольник называется равнобедренным?
Давайте посмотрим на такой треугольник:
На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.
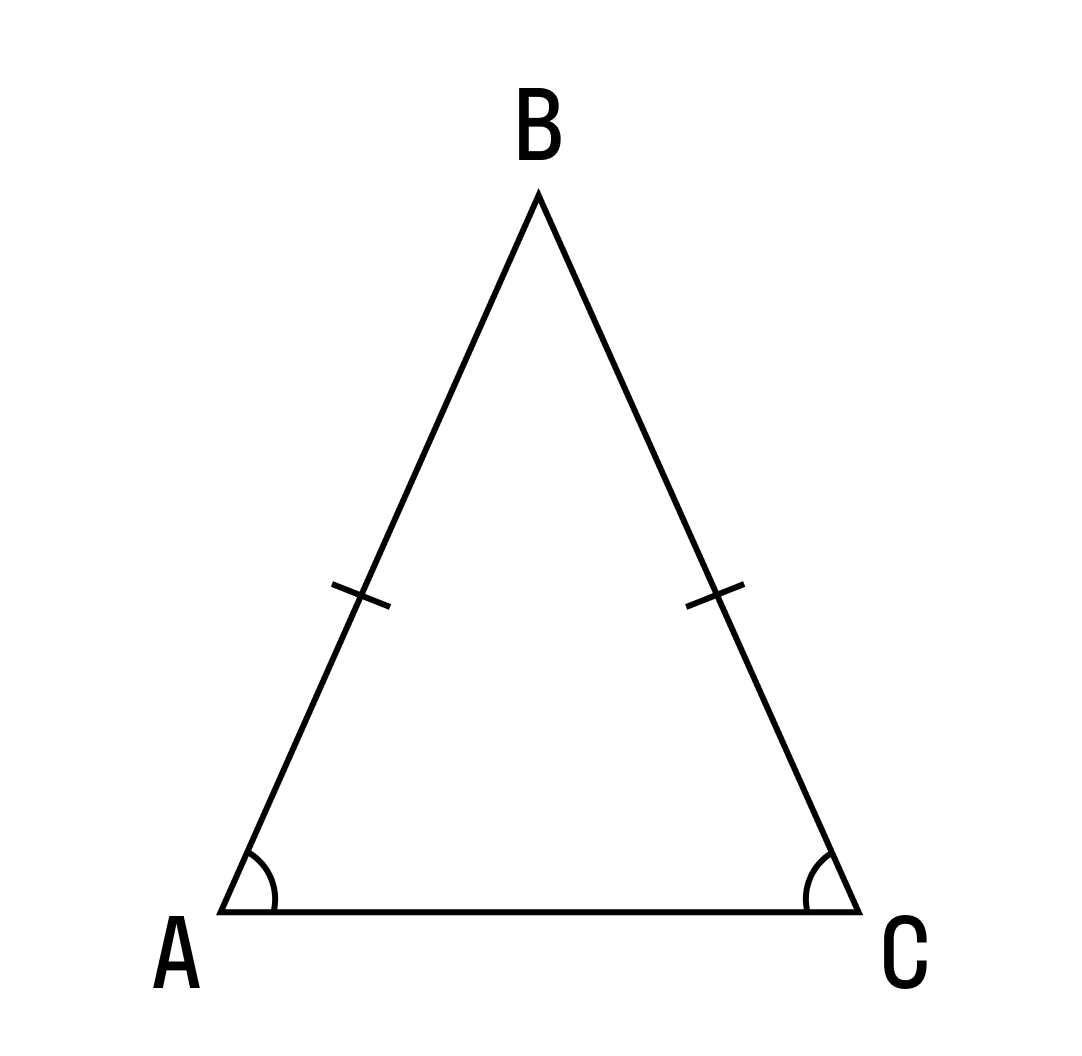
А вот как называются стороны равнобедренного треугольника:
AB и BC — боковые стороны,
AC — основание треугольника.
Чтобы найти основание равнобедренного треугольника, используйте формулу: b = 2a cos
Свойства равнобедренного треугольника
Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 5 теорем.
Теоремы помогут доказать, что треугольник равнобедренный, а не какой-нибудь ещё. Давайте приступим.
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Мы выяснили, что AС — основание равнобедренного треугольника. Поскольку боковые стороны треугольника равны AB = СB, то и углы при основании — равны. ∠ BАC = ∠ BСA. Изи!
Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Чтобы доказать все эти теоремы, вспомним, что такое биссектриса, медиана и высота.
Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.
Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.
Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.
Медиана — линия, которая соединяет вершину треугольника с серединой противолежащей стороны.
Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».
В данном треугольнике медианой является отрезок BH.
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону.
Высотой в представленном равнобедренном треугольнике является отрезок BH.
Доказательство теорем 2, 3, 4 будет коллективным, поскольку из определений видно, что биссектриса, медиана и высота равнобедренного треугольника — это одно и то же.
А вот и доказательство:
Вуаля, сразу три теоремы доказаны.
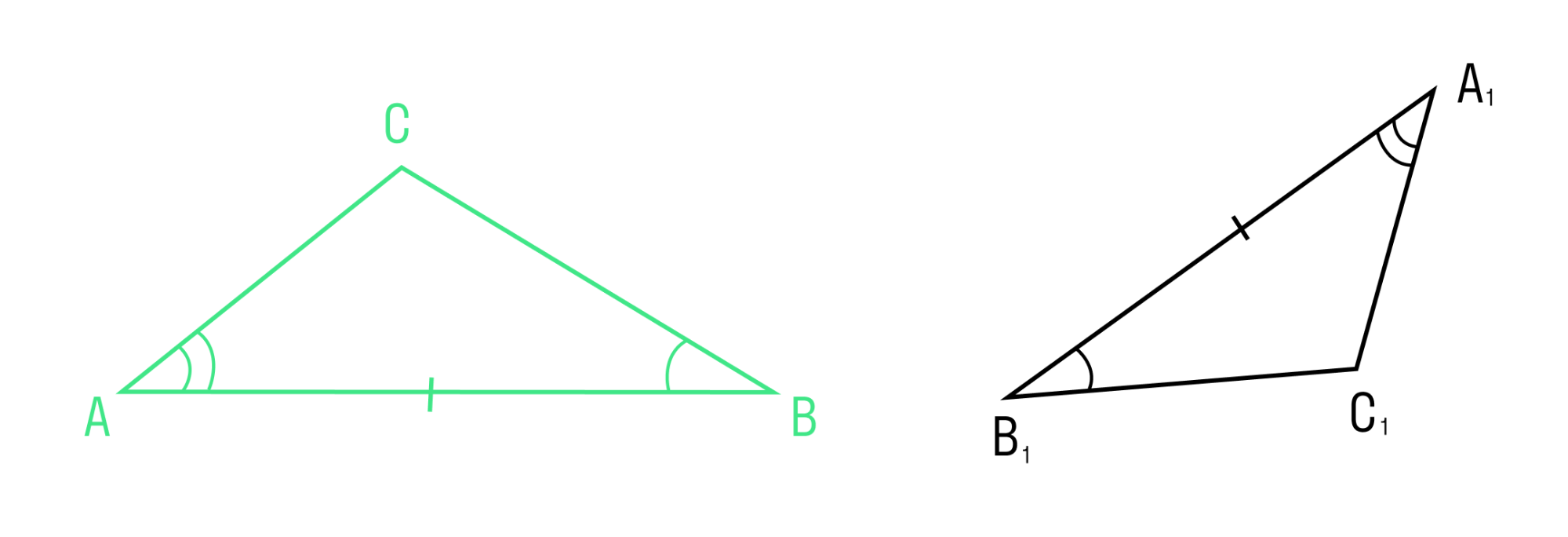
Теорема 5: Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны (третий признак равенства треугольников).
Дано два Δ ABC = Δ A1B1C1.
Чтобы доказать равенство треугольников, мысленно наложите один треугольник на другой так, чтобы стороны совпали. Точка A должна совпасть с точкой А1, точка B должна совпасть с точкой B2, точка С — с точкой С1.
Если все стороны совпадают — треугольники равны, а теорема доказана.
Признаки равнобедренного треугольника
Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.
Формулы равнобедренного треугольника
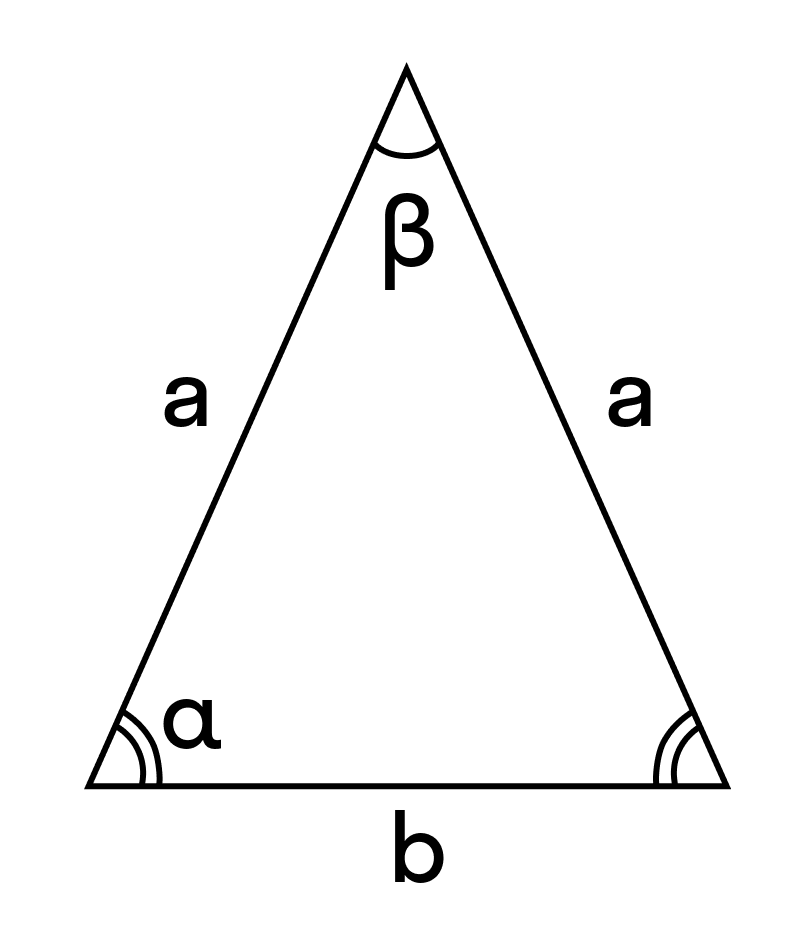
Формулы сторон равнобедренного треугольника
b — основание равнобедренного треугольника
a — равные стороны равнобедренного треугольника
α — углы при основании
β — угол, образованный равными сторонами
Формулы длины стороны (основания b) равнобедренного треугольника
Формулы длины равных сторон равнобедренного треугольника (стороны a):
Формулы высоты, медианы, биссектрисы равнобедренного треугольника
b — основание равнобедренного треугольника
a — равные стороны равнобедренного треугольника
α — углы при основании
β — угол, образованный равными сторонами
L — высота, биссектриса и медиана
Формулы высоты, биссектрисы и медианы равнобедренного треугольника, через сторону и угол (L)
Формула высоты, биссектрисы и медианы равнобедренного треугольника, через стороны (L)
Примеры решения задач
Нет ничего приятнее, чем поупражняться и поискать градусы и длины в равнобедренном треугольнике. Ну… почти ничего.
Задачка раз. Дан ABC: ∠C = 80∘, AB = BC. Найдите ∠B.
Поскольку вы уже знакомы с пятью теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны.
∠A = ∠C = 80∘.
Не должно вас удивить и то, что сумма углов треугольника равна 180∘
∠B = 180∘ − 80∘ − 80∘ = 20∘.
∠B = 20∘
Задачка два. В равнобедренном треугольнике один из углов равен 110∘. Найдите наибольший из внешних углов этого треугольника.
Вспоминаем первую теорему о равенстве углов при основании (а лучше не забываем вовсе). Поскольку сумма углов = 180∘, то второго угла в 110∘ в нём быть не может. Соответственно, известный угол в 110∘ — это угол при вершине. (180∘−110∘)/2=35∘. Внешние углы треугольника равны: 180∘−110∘=70∘,180∘−35∘=145∘,180∘−35∘=145∘. Больший внешний угол равен 145∘
Основы геометрии
Идеальные объекты
Геометрия — раздел математики, который изучает пространственные структуры и отношения, а также их обобщения.
Основные геометрические объекты: окружность, квадрат, ромб, прямоугольник, равносторонний треугольник, равнобедренный треугольник, правильный многоугольник, эллипс и другие.
Все эти фигуры обладают двумя свойствами:
Равенство частей можно заметить у квадрата, ромба или равностороннего треугольника — равенство сторон. Также у них есть одна или несколько линий симметрии.
У шара бесконечное количество осей симметрии и плоскостей симметрии, но отсутствует равенство или подобие составных частей.
Все типы правильных многогранников обладают симметрией, при этом составлены из некоторого количества одинаковых фигур (треугольников, квадратов, пятиугольников).
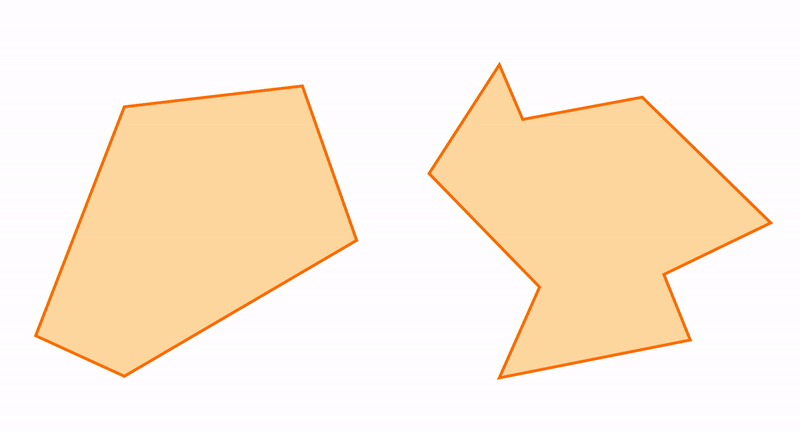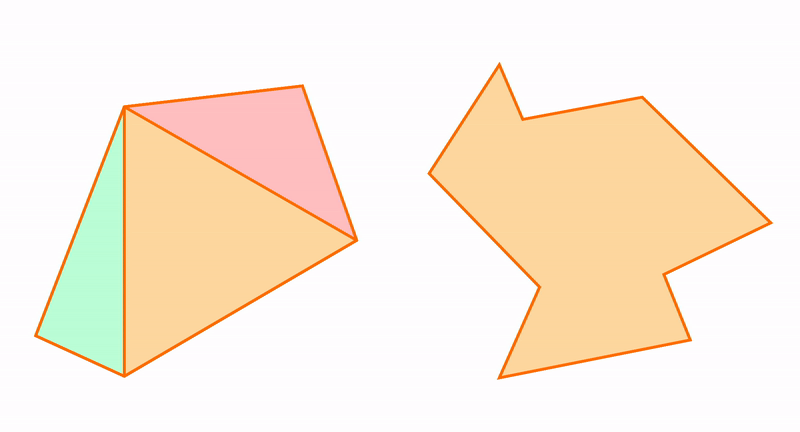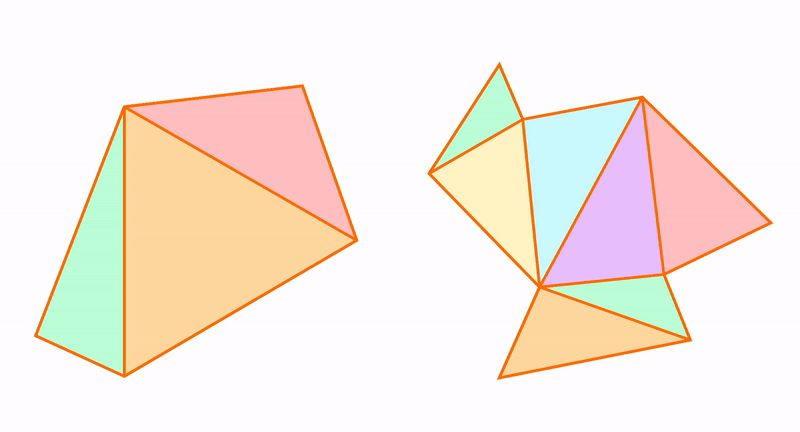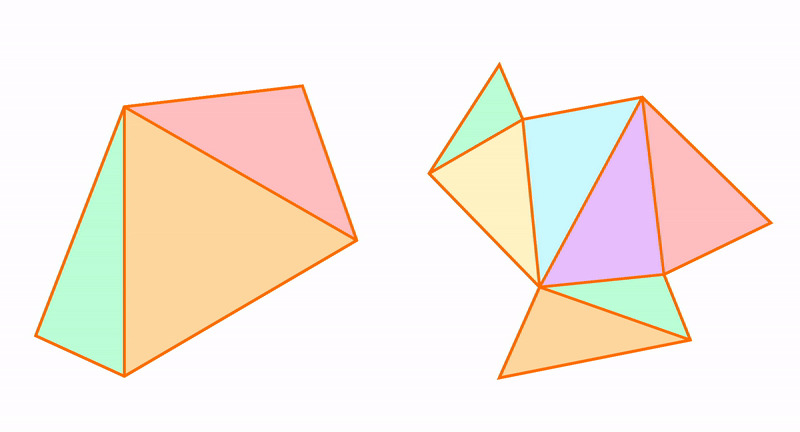
Из всего этого можно сделать вывод, что отличить правильную геометрическую фигуру от произвольной совсем не сложно. Достаточно выяснить, имеет ли данная фигура оси или плоскости симметрии, а также из каких повторяющихся частей она состоит.
Таким образом, именно по наличию или отсутствию симметрии и равенства или подобия составных частей можно оценивать различные объекты окружающего мира на соответствие правильному геометрическому виду.
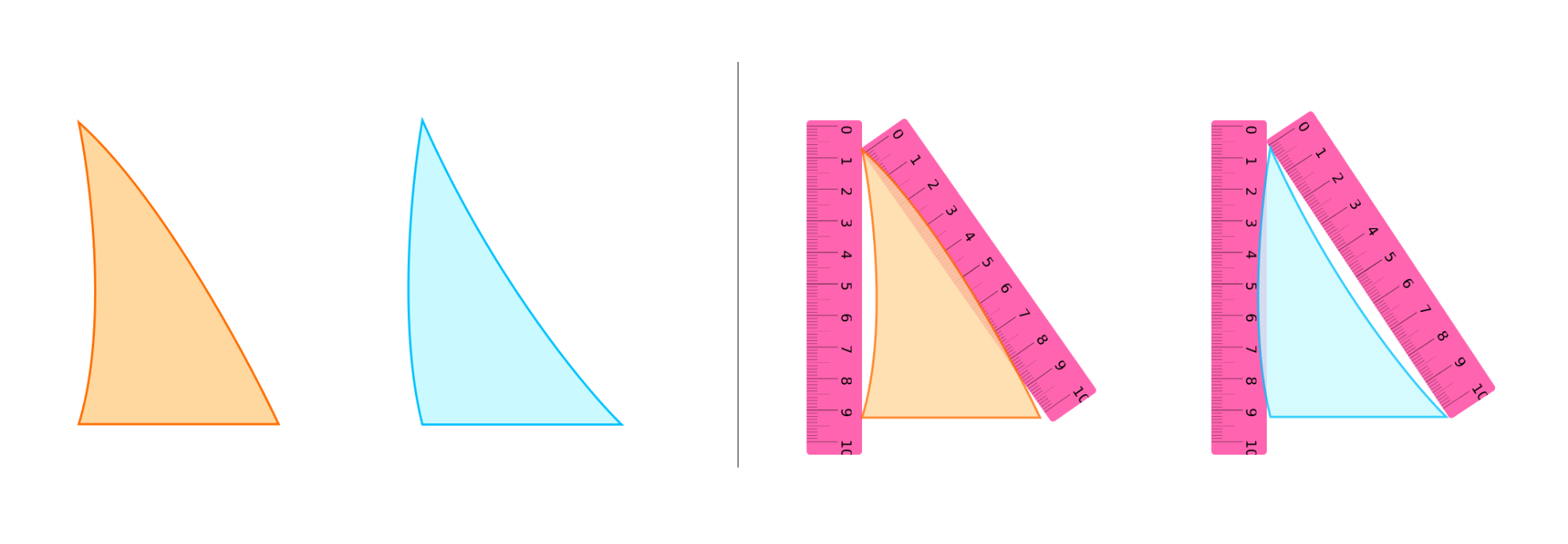
Например, возьмем два треугольника. На первый взгляд, они похожи, но у одного из них одна сторона вогнутая, вторая — выпуклая. А у другого наоборот.
Математика занимается идеальными объектами и делает о них некие заключения, которые называют теоремами. Эти треугольники похожи, и о них можно сделать близкое заключение, которое будет описывать свойства обоих.
Например, теорема Пифагора звучит так: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. А затем это свойство можно применять при решении задач и составлении чертежей.
Базовые геометрические объекты
Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.
Точка — это идеальный математический объект, у которого нет длины и ширины.
Отрезок — это часть прямой, у которого есть начало и конец.
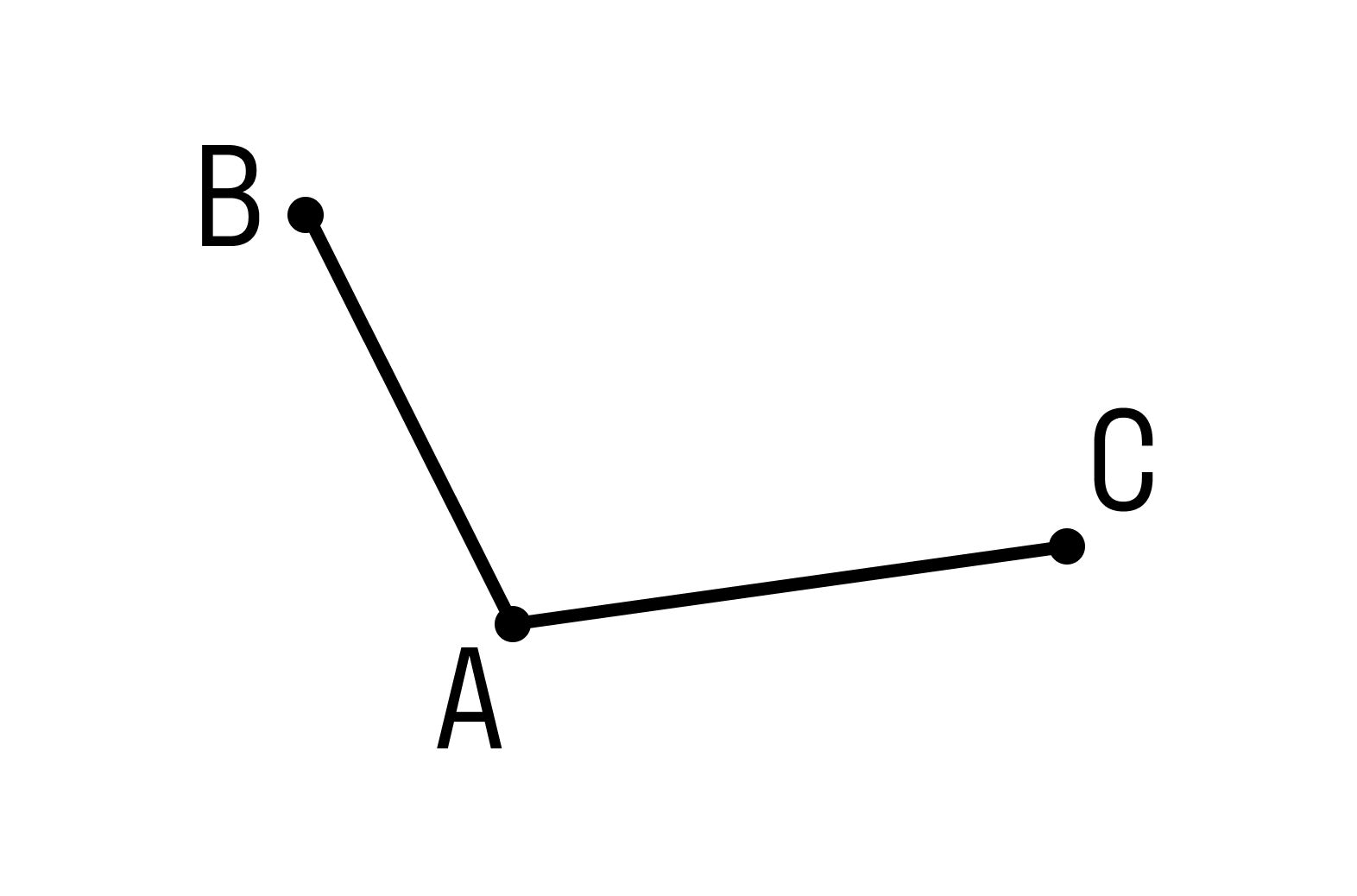
Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец. На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.
Прямая — это «не кривая». Более точное определение вряд ли можно сформулировать.
Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.
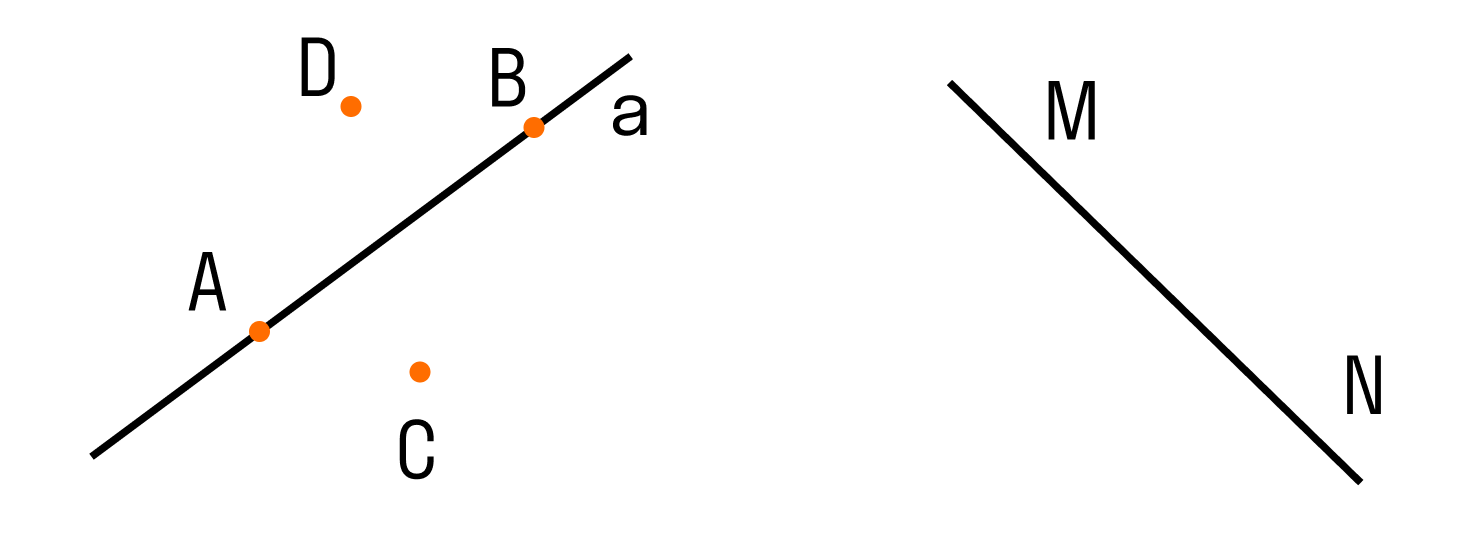
Обозначать прямые принято малыми латинскими буквами (a, b,c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).
Два варианта расположения точек относительно прямой:
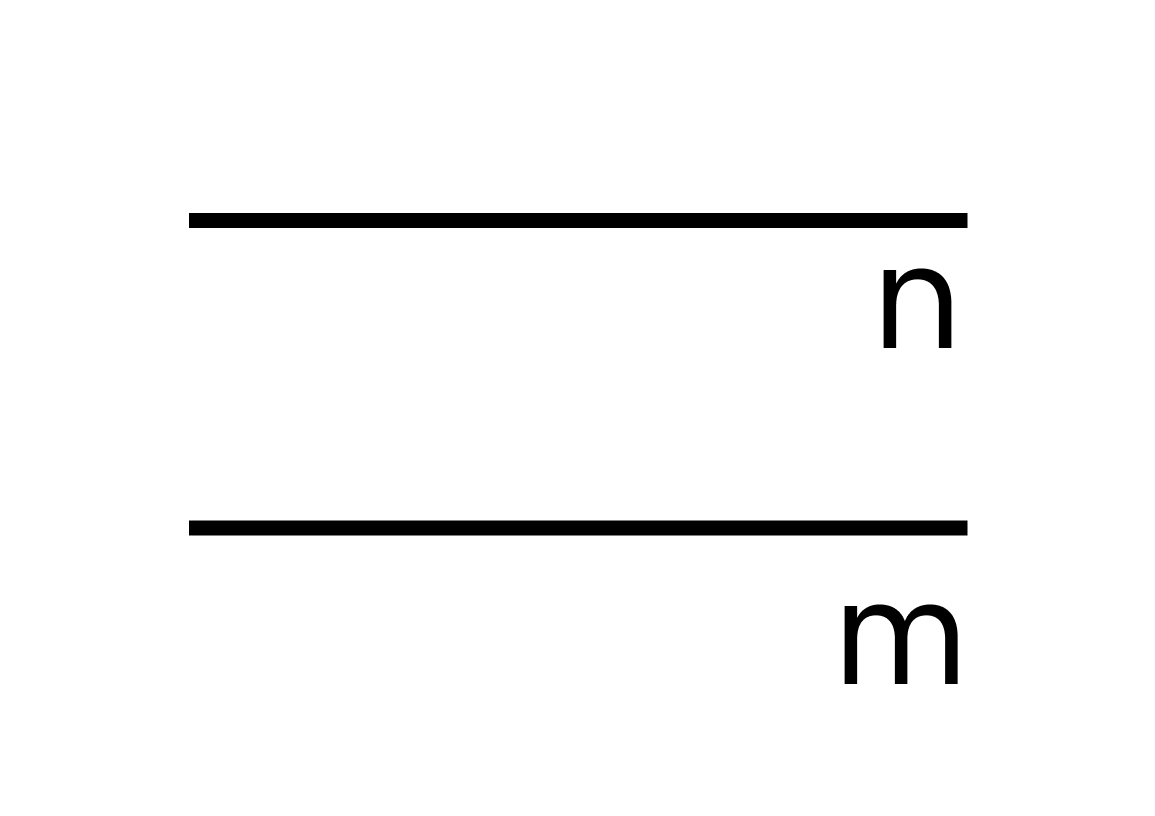
Если рассмотреть две прямые, то возможны два варианта их расположения:
Для записи не пересекающихся прямых используют специальный знак — 
то есть m 
Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.
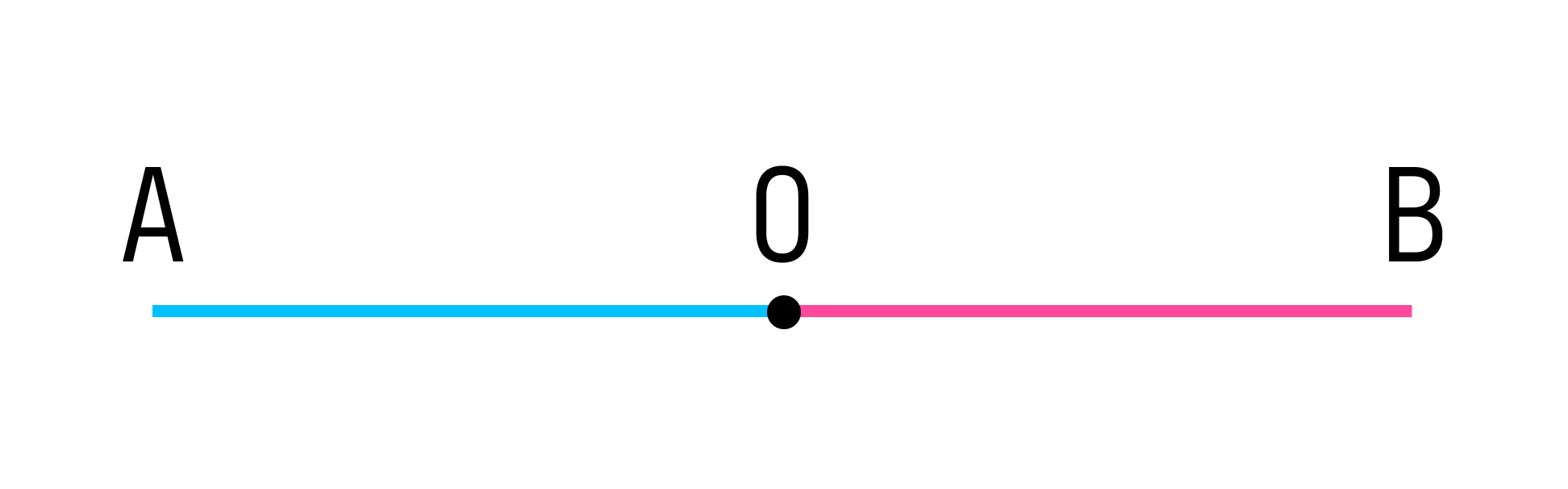
На рисунке точка О разбивает прямую АВ на две части:
Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.
Назовем получившиеся лучи:
Лучи ОА и ОВ принадлежат одной прямой АВ. Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.
Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости
Комбинации простейших объектов
Поговорим про комбинации простейших объектов. Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).
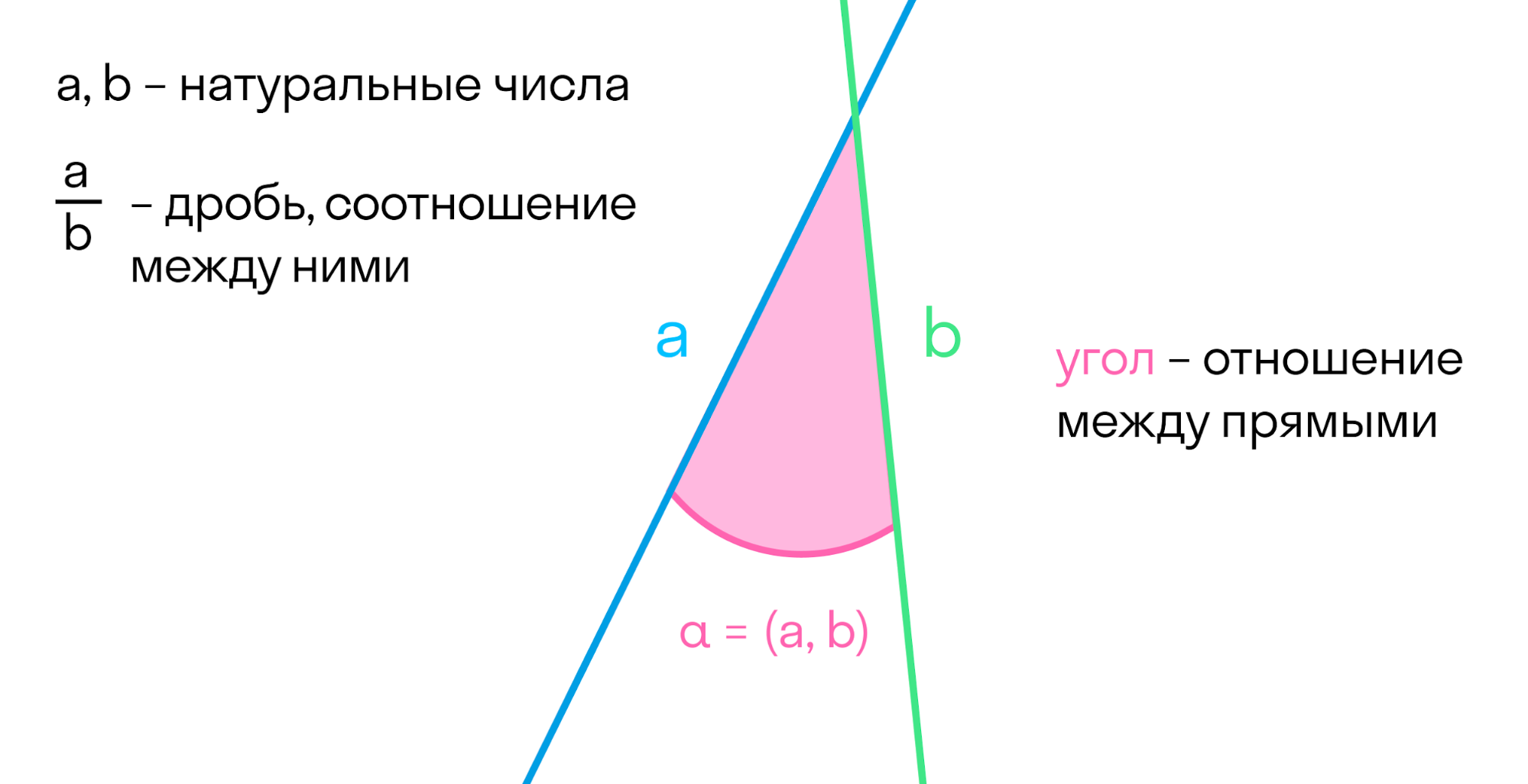
Когда прямые пересекаются, можно ввести понятие отношения между двумя прямыми. Аналогично мы поступали с числами: ввели натуральные числа — количество предметов в множестве. А после этого изучали отношения между этими числами: дроби, возведение в степень.
Точно так же мы изучали множества, а после — отношения между множествами, функции.
Две прямые образуют углы. По сути, угол — это отношение между прямыми. Если один из них нулевой, то прямые параллельны. Если нет — прямые пересекаются.
Максимальный угол – это полный оборот, он составляет 360 градусов.
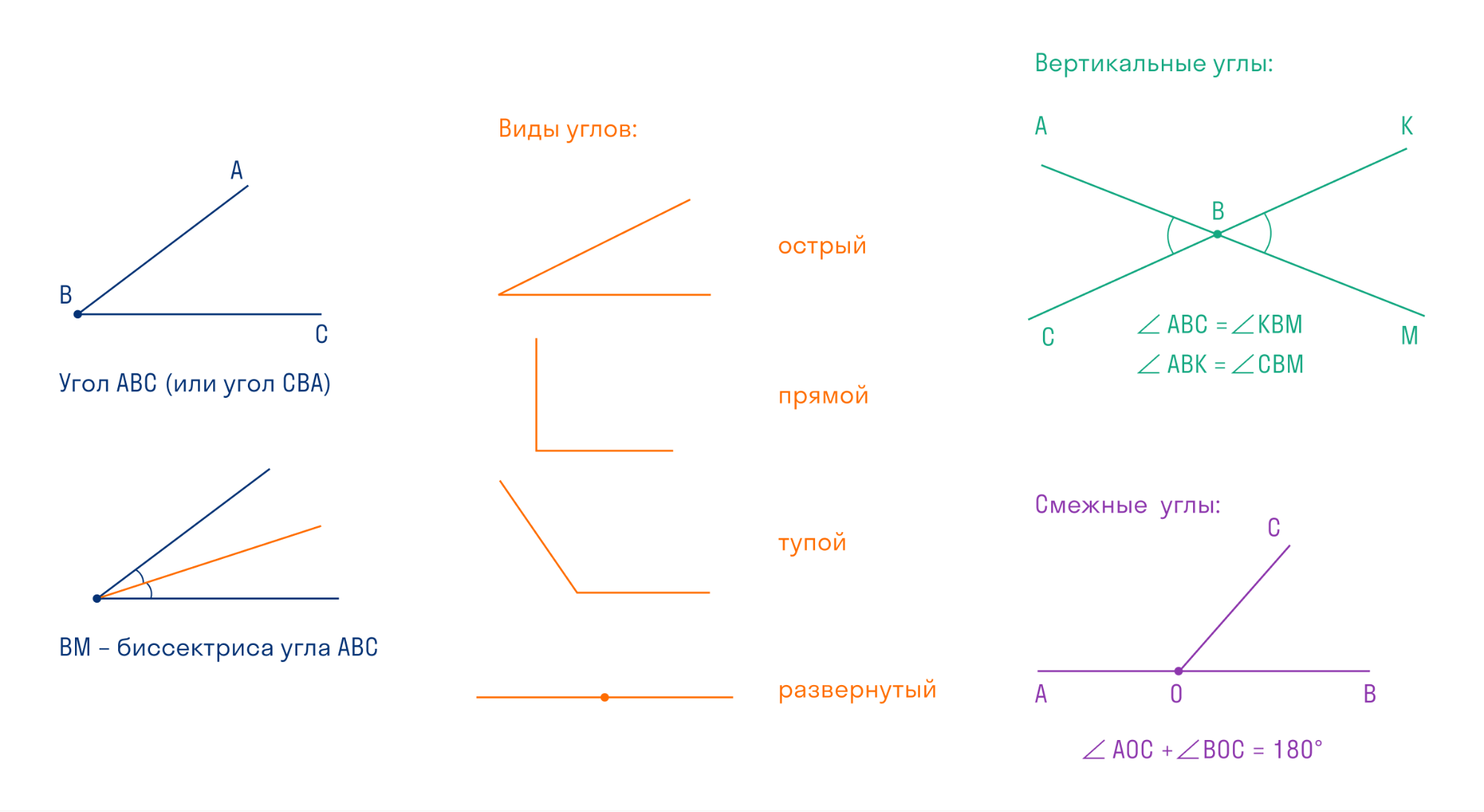
Угол — это часть плоскости, ограниченная двумя лучами, которые выходят из одной точки. Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.
Есть разные виды углов, выделим самые часто встречающиеся:
Точка называется вершиной угла, а лучи — сторонами угла.
Два угла называются вертикальными, если их стороны являются дополнительными лучами. Свойство вертикальных углов звучит так: вертикальные углы равны.
Два угла называются смежными, если одна сторона у них общая, а две другие являются дополнительными лучами. Свойство смежных углов: сумма смежных углов равна 180°.
Биссектриса угла — это луч с началом в вершине угла, который делит угол на две равные части.
А теперь посмотрим на взаимное расположение трех прямых.
Первый случай: все три прямые параллельны.
Второй случай: две прямые параллельны, а третья их пересекает.
Третий случай: если провести три прямые на плоскости случайным образом, велика вероятность образования треугольника. Поэтому этой фигуре мы уделяем так много времени в школе на уроках геометрии.
Треугольник
Треугольник образуют три прямые. Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.
Из треугольников можно получить остальные многоугольники и к треугольникам можно приближать другие фигуры. Например, пятиугольник состоит из трех треугольников.
Треугольник можно использовать для измерения расстояний. А еще треугольник можно рассматривать в отношениях с окружностью, которая тоже является элементарной конструкцией. Читайте про вписанные и описанные углы.
Треугольник можно легко вычислить, то есть найти его площадь по трем элементам:
Приходи на наши онлайн уроки по математике с лучшими препадавателями! Для учеников с 1 по 11 классы!
Свойства треугольников
Раз треугольник можно задать тремя элементами, значит их можно классифицировать. Если два треугольника похожи, значит у них есть общие свойства.
Треугольник можно составить совсем не из любых трех отрезков: они должны удовлетворять важному свойству — неравенству треугольника.
Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет. Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок.
Сумма любых двух сторон треугольника больше его третьей стороны.
Еще одно свойство верное для всех треугольников: сумма всех углов треугольника составляет половину полного оборота. Или по-другому: сумма углов треугольника — два прямых угла.
Мы знаем, что две геометрические фигуры считают равными, если их можно совместить наложением. Это справедливо и для треугольников. Равные фигуры имеют равные размеры и формы. Значит, если два треугольника равны — элементы одного треугольника соответственно равны элементам другого треугольника.
Равенство треугольников ABC и A1B1C1 обозначается так: ΔABC = ΔA1B1C1.
Есть даже специальные теоремы про равенство треугольников.
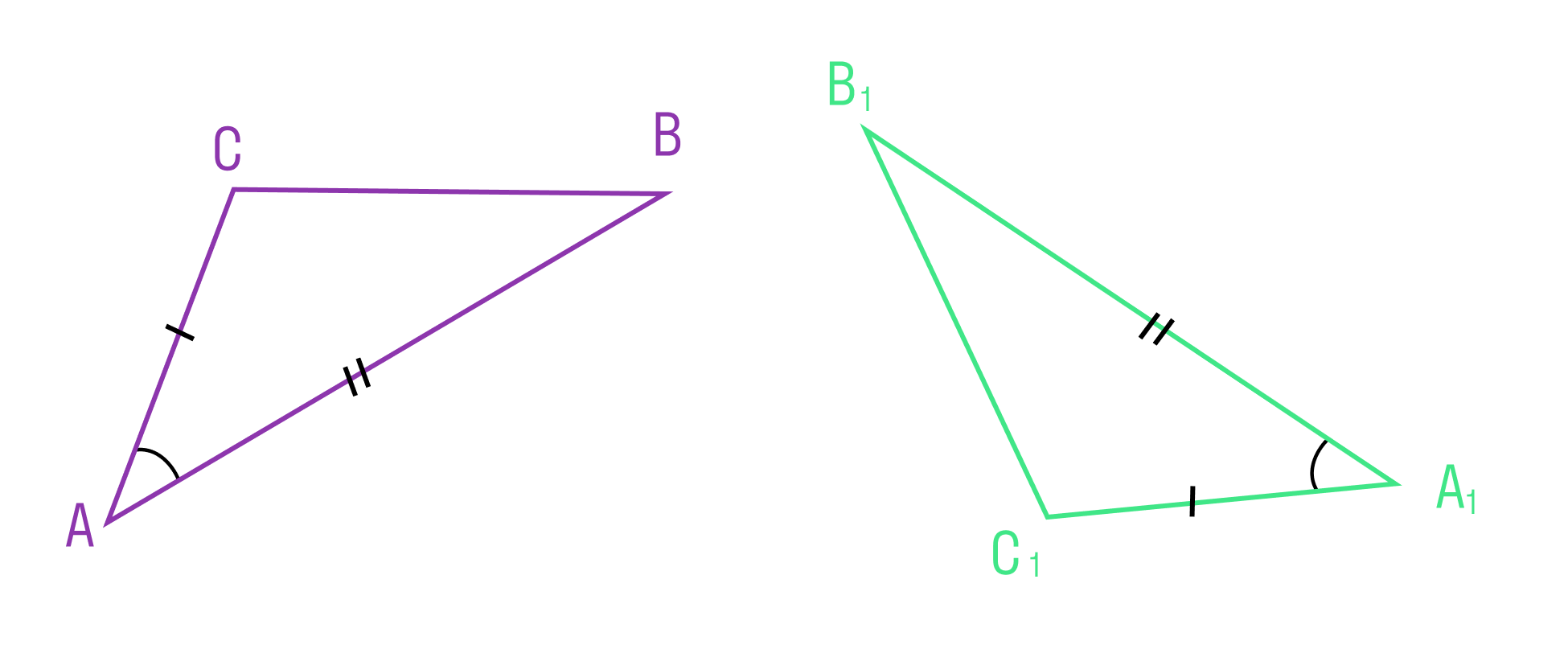
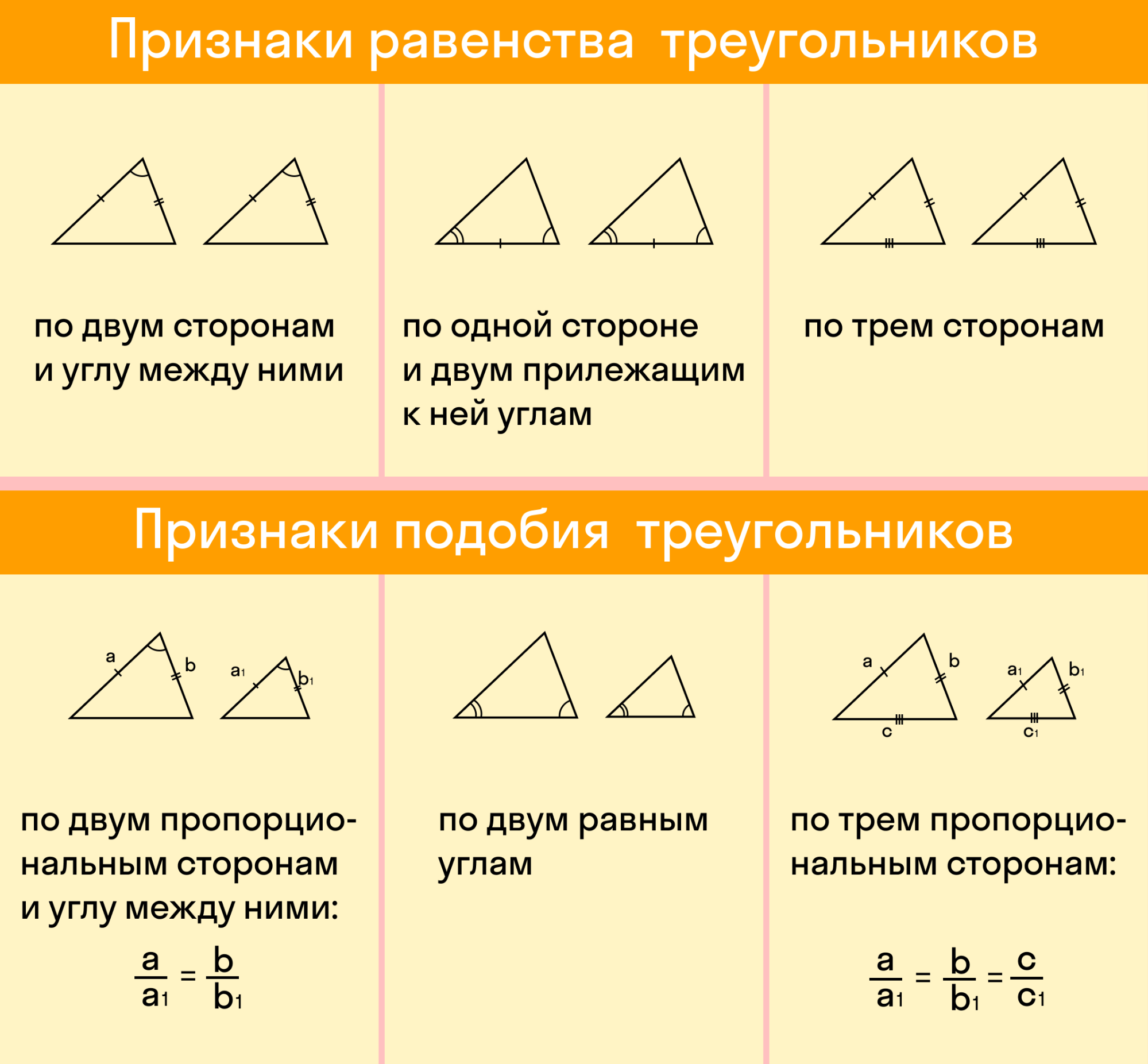
Первый признак равенства треугольников звучит так:
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны
Второй признак равенства треугольников
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
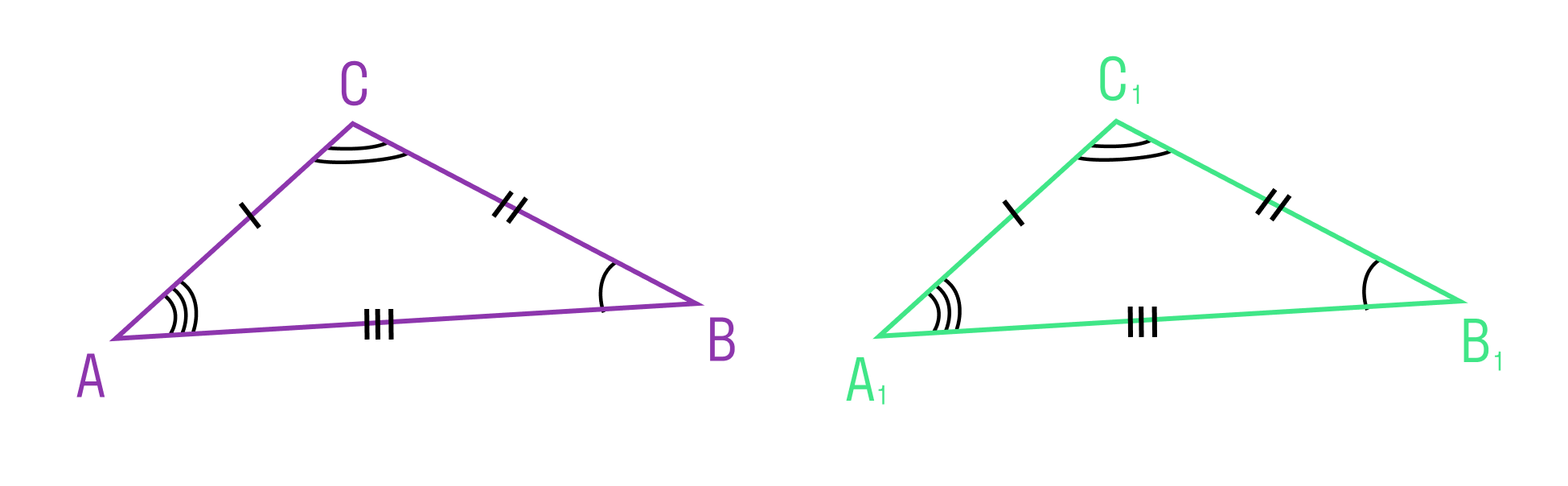
Третий признак равенства треугольников
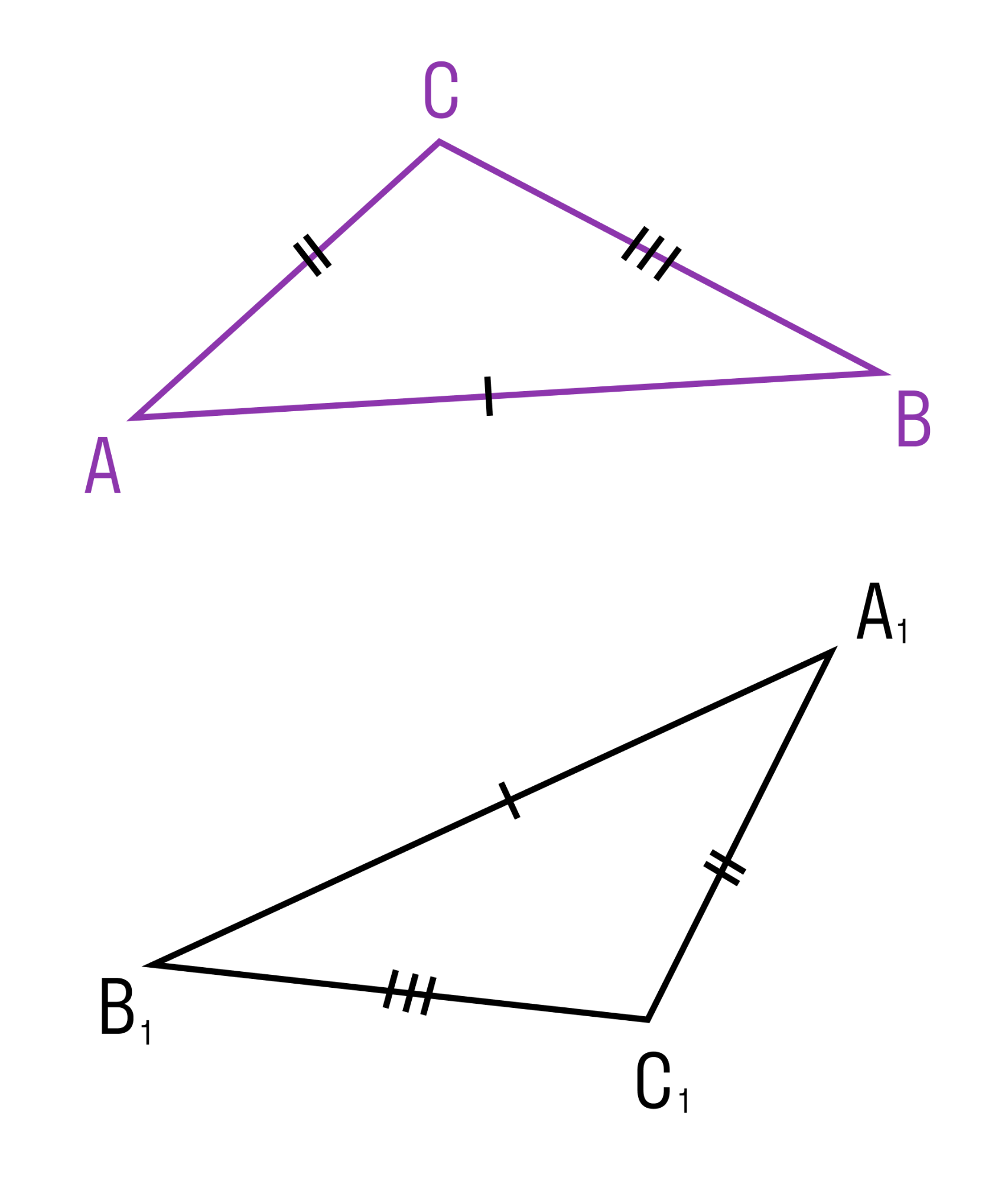
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Из теоремы следует, что треугольник — жесткая фигура, то есть фигура, которую невозможно деформировать.
Подобные треугольники
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
Треугольники АВС и A1B1C1 будут подобны, если
Число k, которое равно отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
Подобие треугольников обозначают специальным символом — ∾. На рисунке треугольники АВС и A1B1C1 подобны, это можно записать так: ΔАВС ∾ ΔA1B1C1.
Теорема о первом признаке подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такое треугольники подобны.
Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны — такие треугольники подобны.
Третий признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
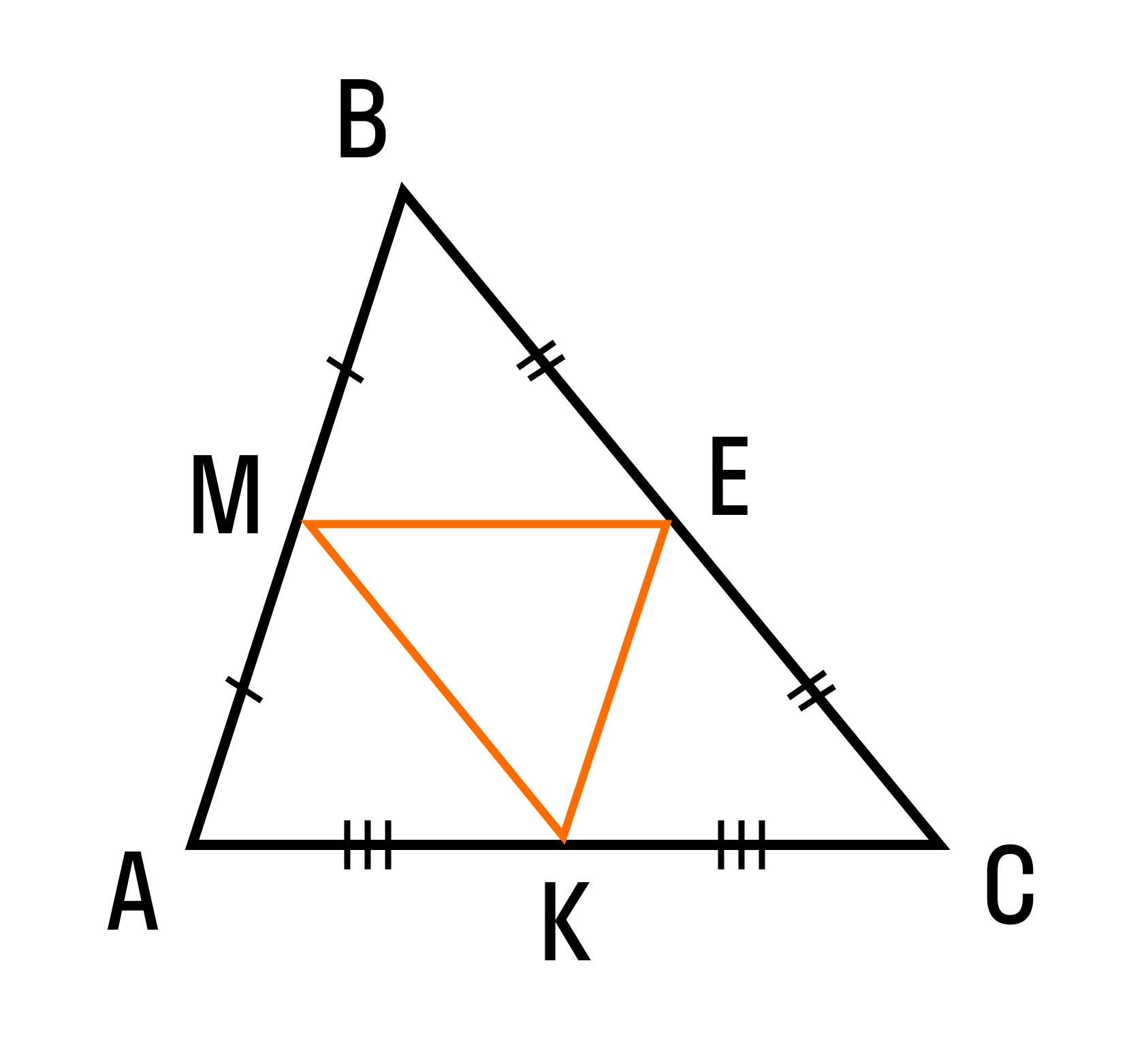
Средняя линия треугольника — это отрезок, который соединяет середины двух его сторон. В каждом треугольнике можно провести три средних линии, при пересечении которых получается четыре равных треугольника, подобных исходному с коэффициентом подобия 1/2.
На рисунке изображен треугольник АВС. Отрезки МЕ, МК и КЕ — средние линии данного треугольника, ΔВМЕ = ΔАМК = ΔСЕК = ΔМЕК.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
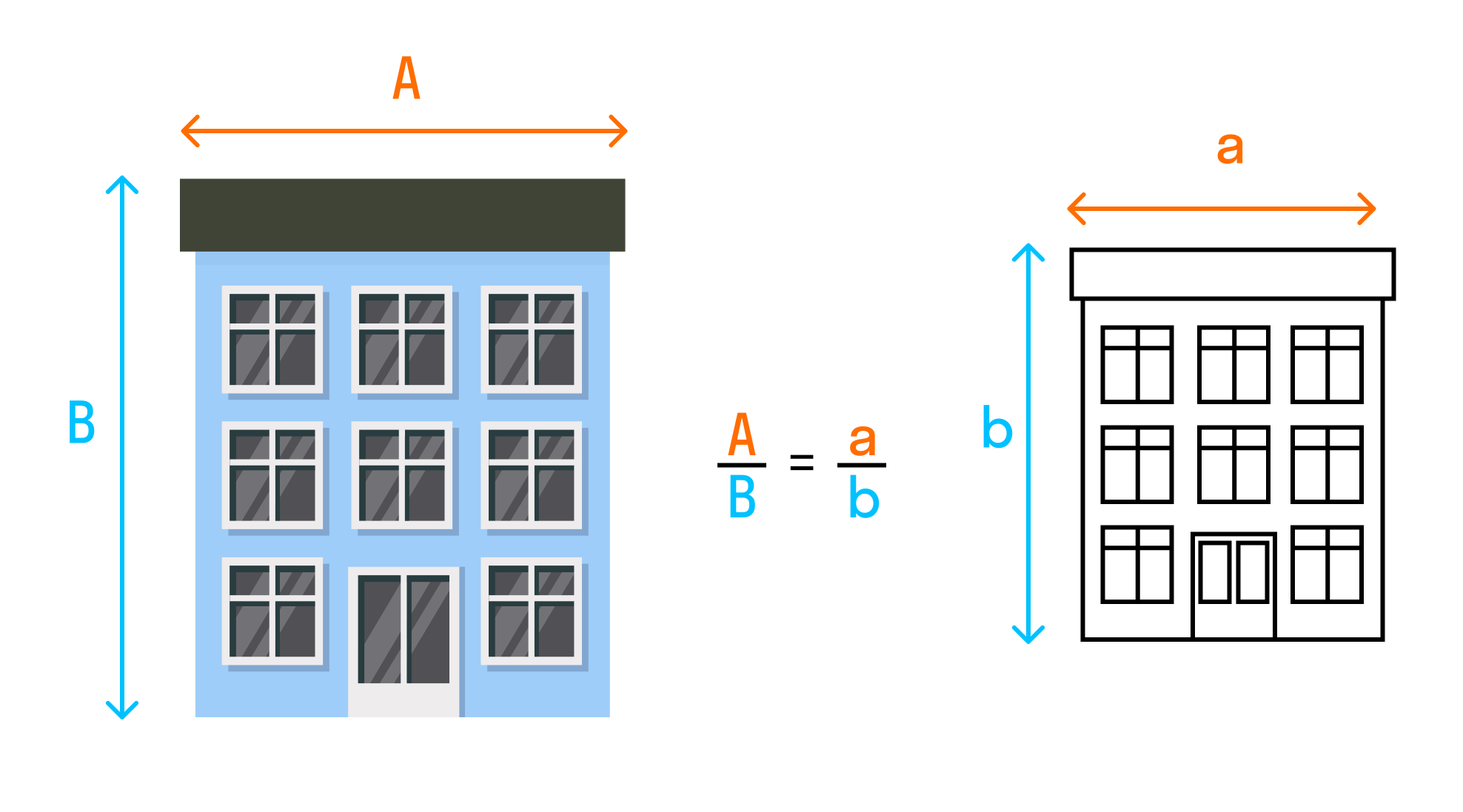
Важно понимать, что подобие в математике — это то, что в обычной жизни мы называем схожестью. Нарисовали треугольники или прямоугольники и говорим, что они похожи потому, что их стороны пропорциональны.
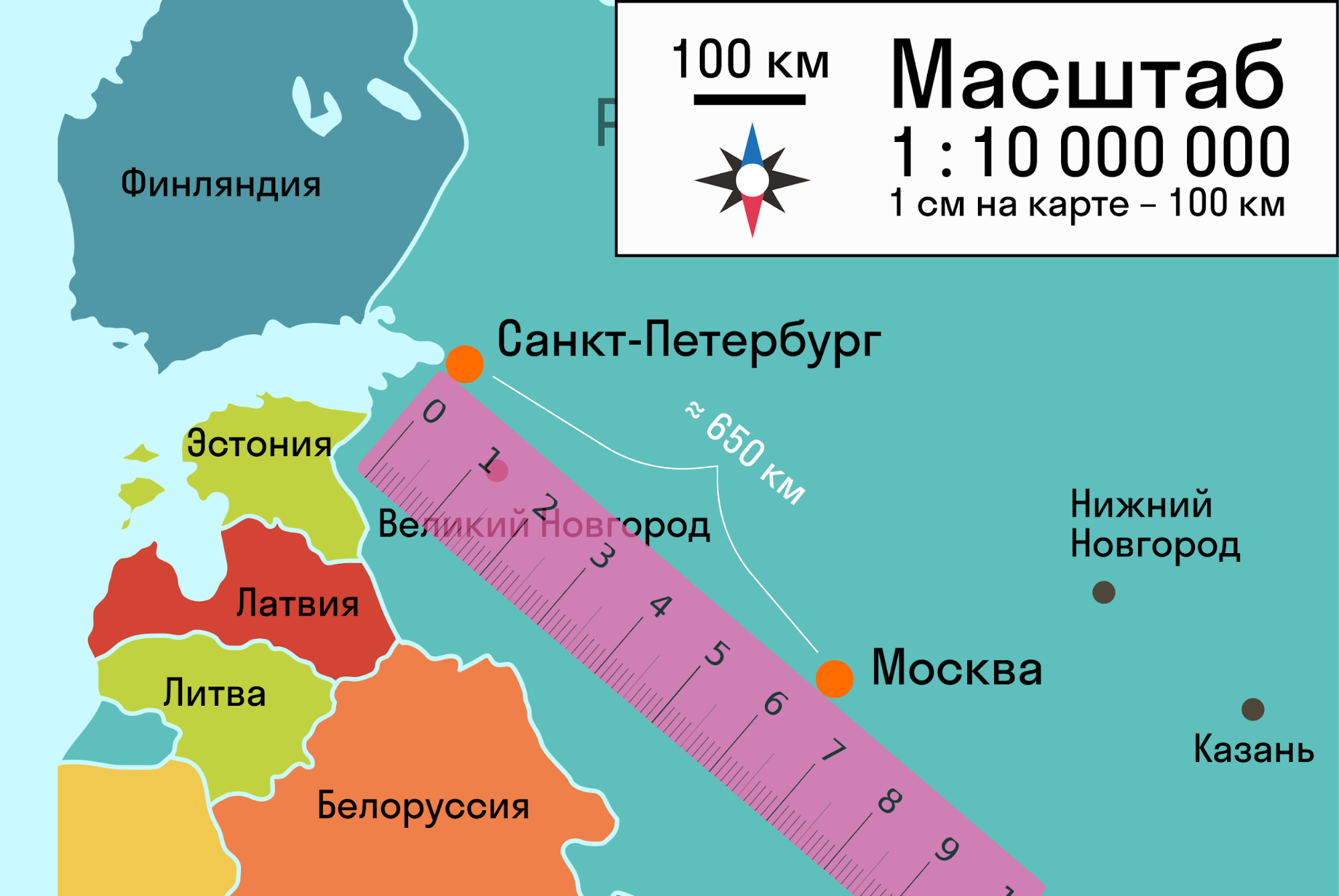
Пример подобия — карта. Она подобна местности, которую отражает. А масштаб — это и есть коэффициент подобия. С треугольниками или другими фигурами точно также.
Классификация треугольников по их сторонам
Для классификации треугольников можно использовать их типологию.
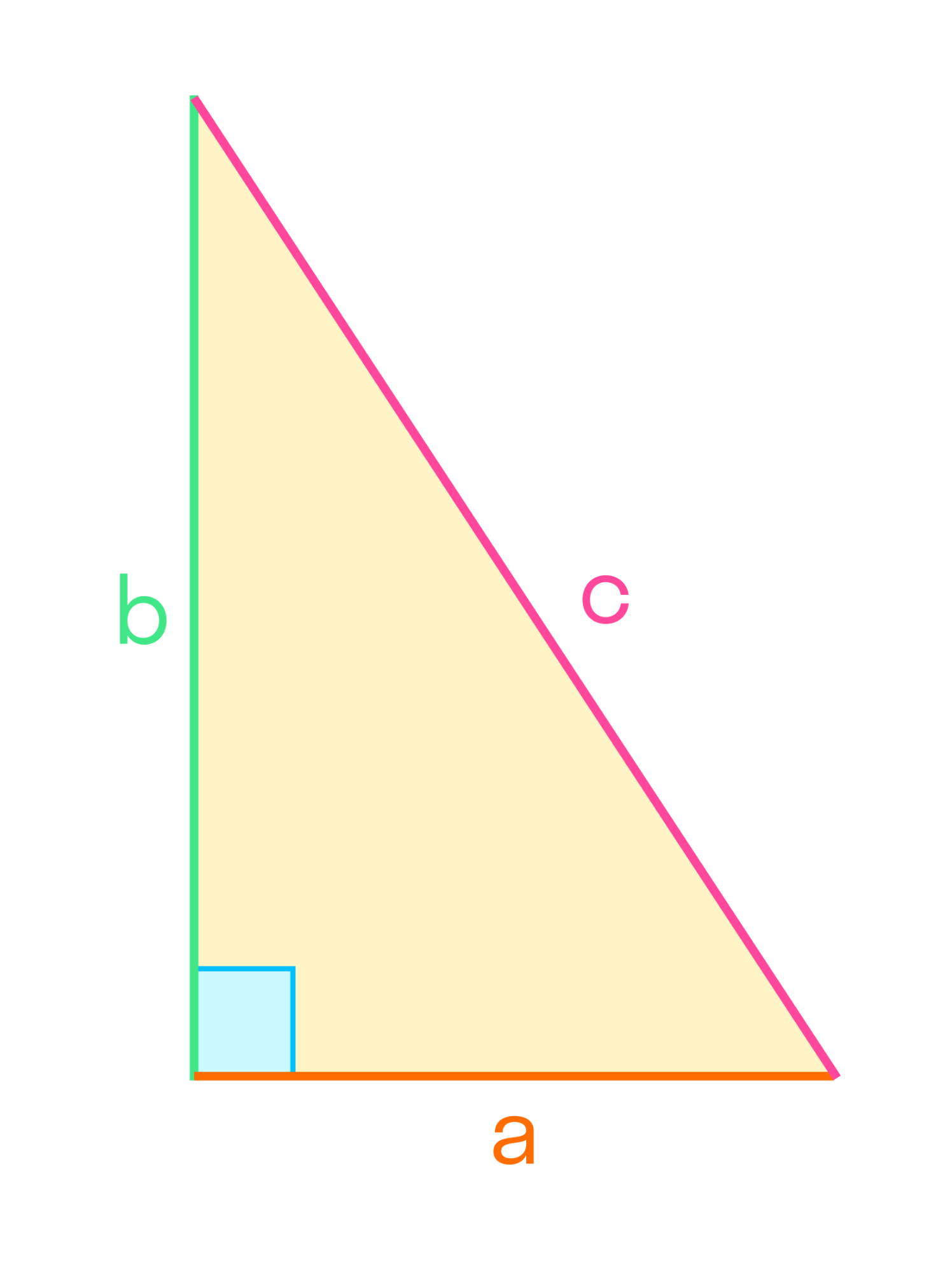
Один из распространенных типов — прямоугольный треугольник. Если один из углов прямой, то это накладывает определенные свойства на треугольник. Прямоугольный треугольник — это также половина прямоугольника.
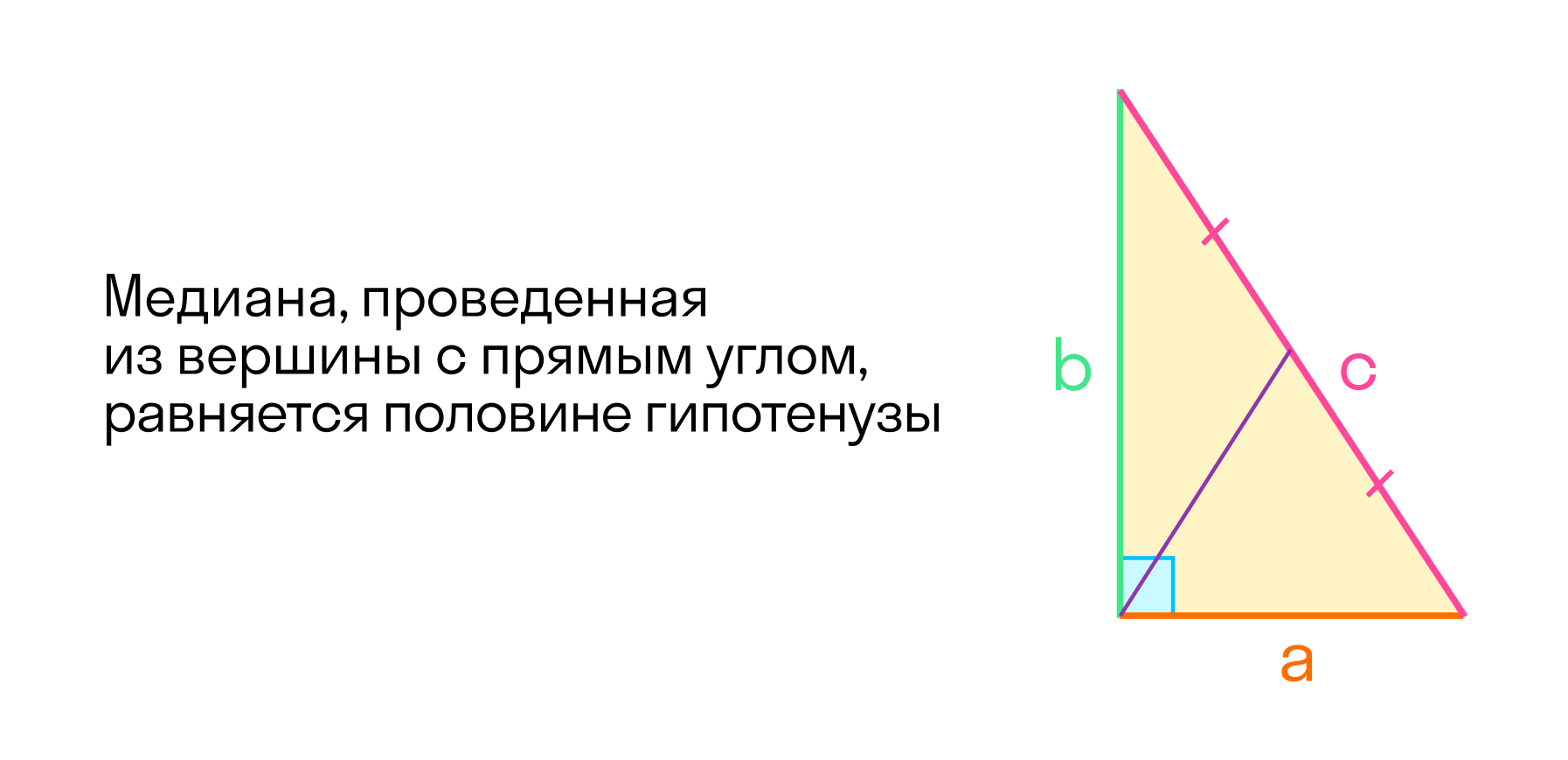
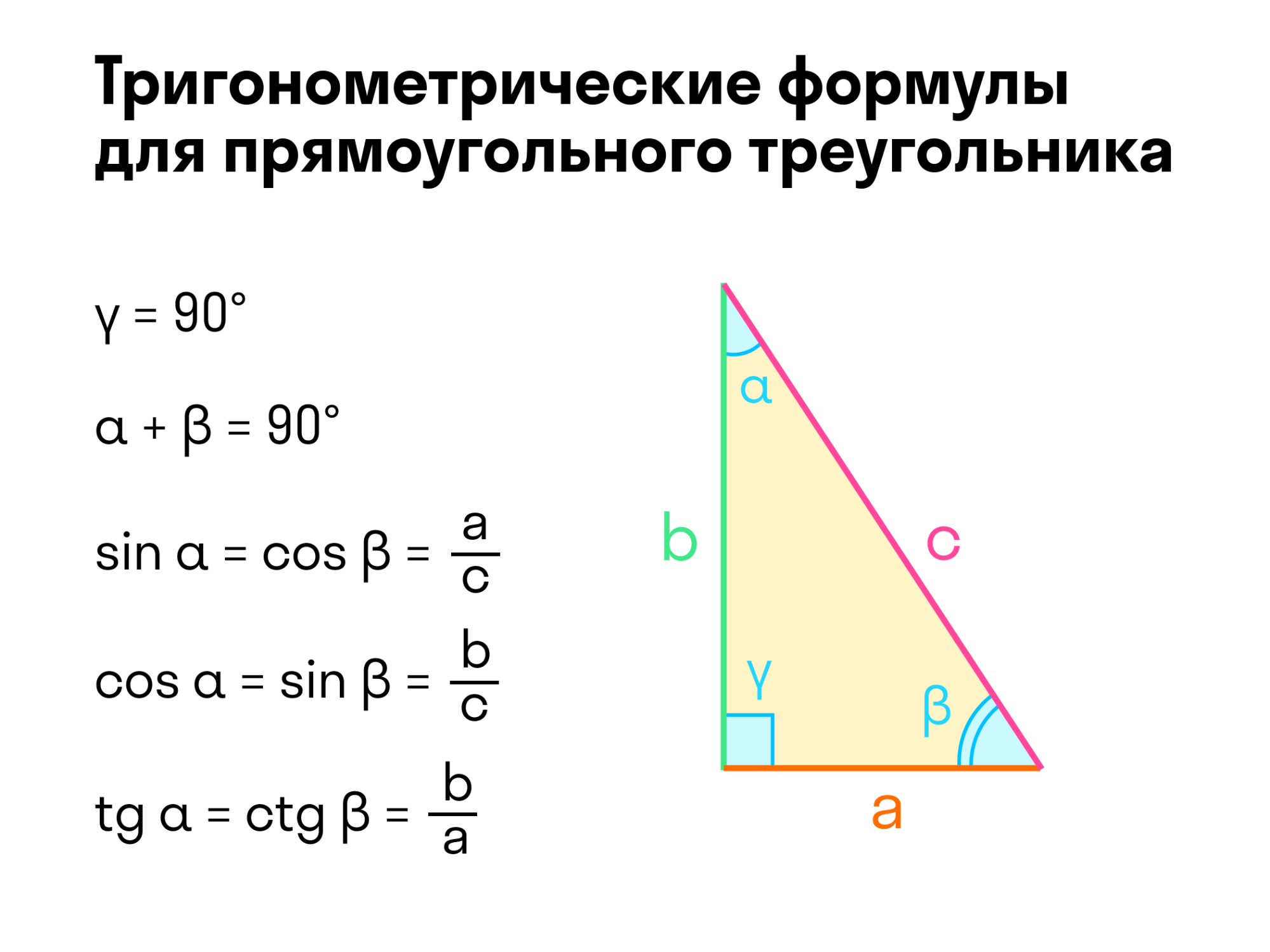
Свойства прямоугольного треугольника
С прямоугольных треугольников начинается изучение тригонометрии. Можно измерять углы с помощью отношений, использовать понятия синуса, косинуса. Помним, что угол можно задать двумя числами, их отношением.
Если две стороны треугольника равны, то это равнобедренный треугольник — и тогда у него есть ось симметрии. Если нарисовать такой треугольник и сложить лист пополам, то две части треугольника совпадут. Эта особенность дает треугольнику определенные свойства.
Симметричный треугольник, у которого все углы и стороны равны — это равносторонний треугольник. У таких треугольников три оси симметрии. Это значит, что если мы повернем треугольник на 60 градусов, то получим точно такой же треугольник.
Такой треугольник задается одним параметром — длиной стороны. Она полностью определяет все другие значения и размеры в этом треугольнике.
От правильного треугольника может плавно перейти к правильным многоугольникам. У треугольника 3 угла, у четырехугольника — 4, а у пятиугольника — 5 углов. У многоугольника много углов🙃
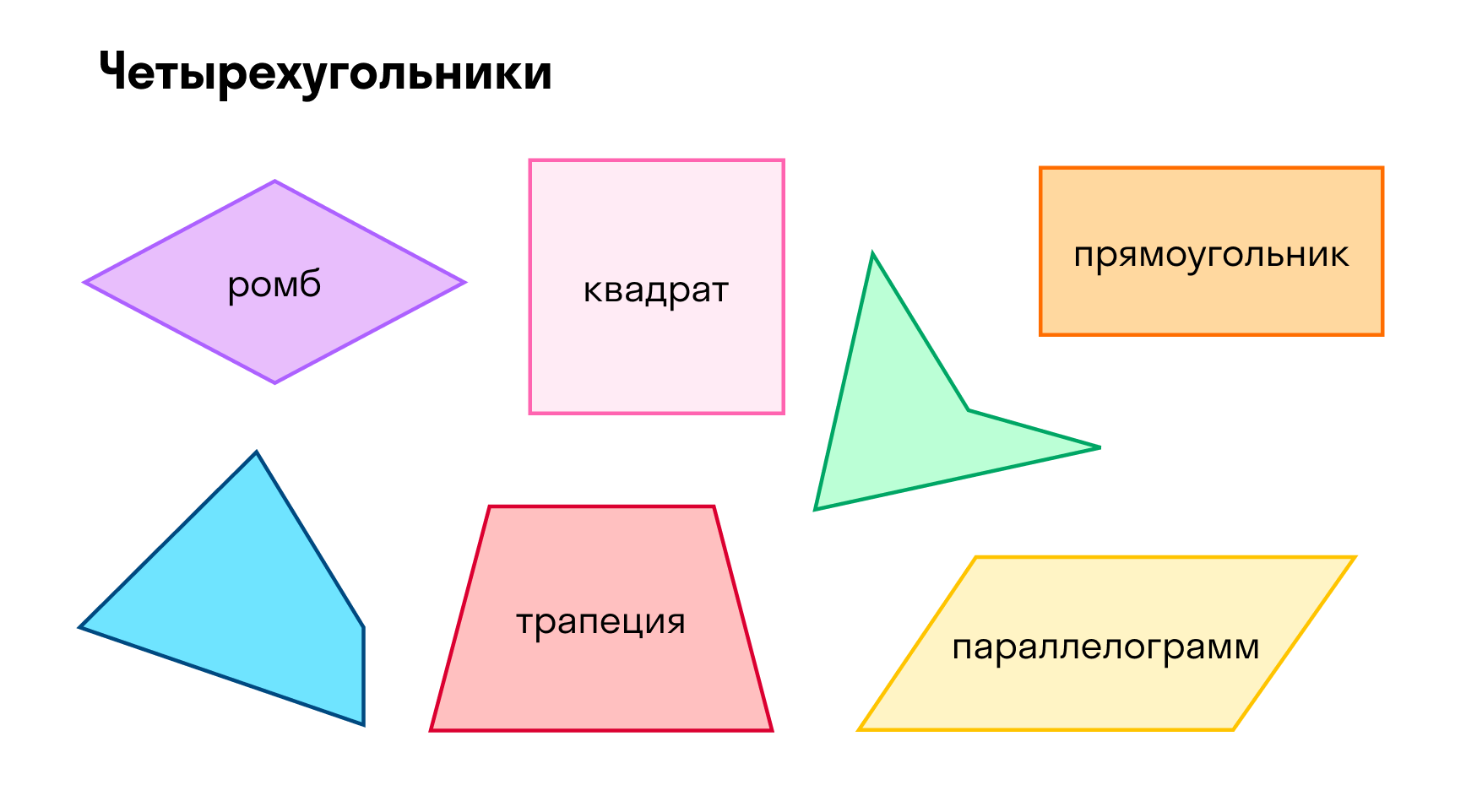
Четырехугольники
Про четырехугольники мы много говорим на уроках в школе: прямоугольник, квадрат, ромб.
Но говорим о них не в общем случае, как для треугольников (такие вещи, как теорема синусов, косинусов), а можем формулировать только какие-то свойства для определенных видов четырехугольников.
Четырехугольникам лучше уделить побольше времени — у каждого из них есть особые свойства, которые не пригодятся для других фигур. Поэтому каждый четырехугольник лучше внимательно изучить на уроке или почитать в наших материалах:
Окружность
Окружность — это еще один объект, который полезно изучить. Ее легко описать, она задается одним параметром — радиусом. А еще часто встречается в физике и в обычной жизни. Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.
Взаимодействие объектов
Следующий уровень — это взаимодействие всех-всех объектов, о которых мы говорили раньше.
Например, окружность и прямая. Прямая может находиться где-то в стороне от окружности, может ее пересекать, а может касаться, то есть пересекать в одной точке.
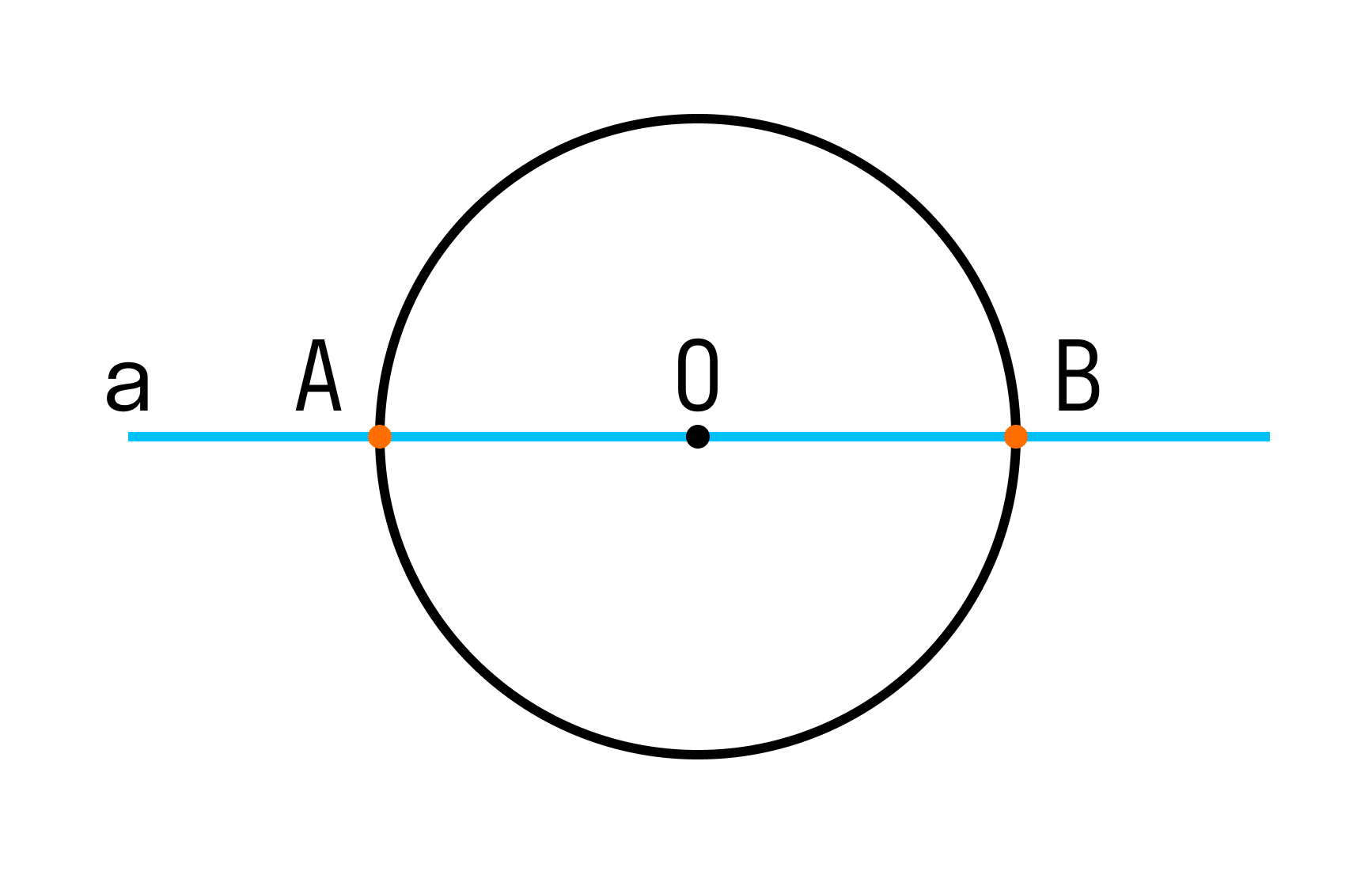
Если прямая проходит через центр окружности, то она пересекает окружность в двух точках — концах диаметра, который лежит на на этой прямой.
На рисунке прямая a проходит через центр окружности (точку О) и пересекает ее в двух точках А и В, которые являются концами диаметра АВ данной окружности.
Если прямая a не проходит через центр О окружности радиуса r, то возможны три случая взаимного расположения прямой и окружности — в зависимости от соотношения между радиусом r этой окружности и расстоянием d от центра окружности до прямой a. Вот эти случаи:
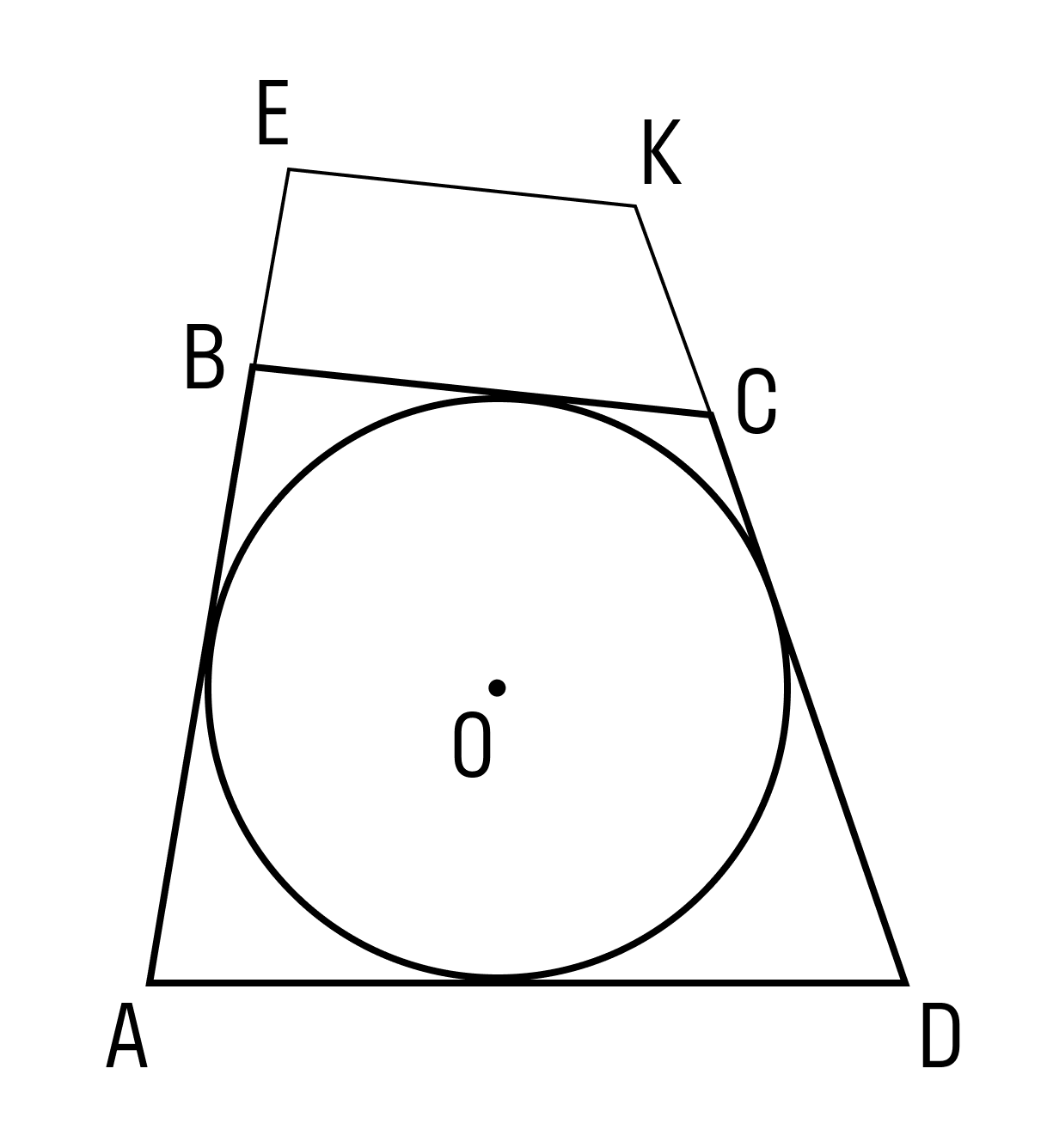
Окружность вписанная в многоугольник — это окружность, которая касается всех сторон многоугольника. Центр вписанной окружности лежит внутри многоугольника, в который она вписана. Описанный около окружности многоугольник — это многоугольник, в который вписана окружность.
На рисунке четырехугольник АВСD описан около окружности с центром О, а четырехугольник АЕКD не является описанным около этой окружности, так как сторона ЕК не касается окружности.
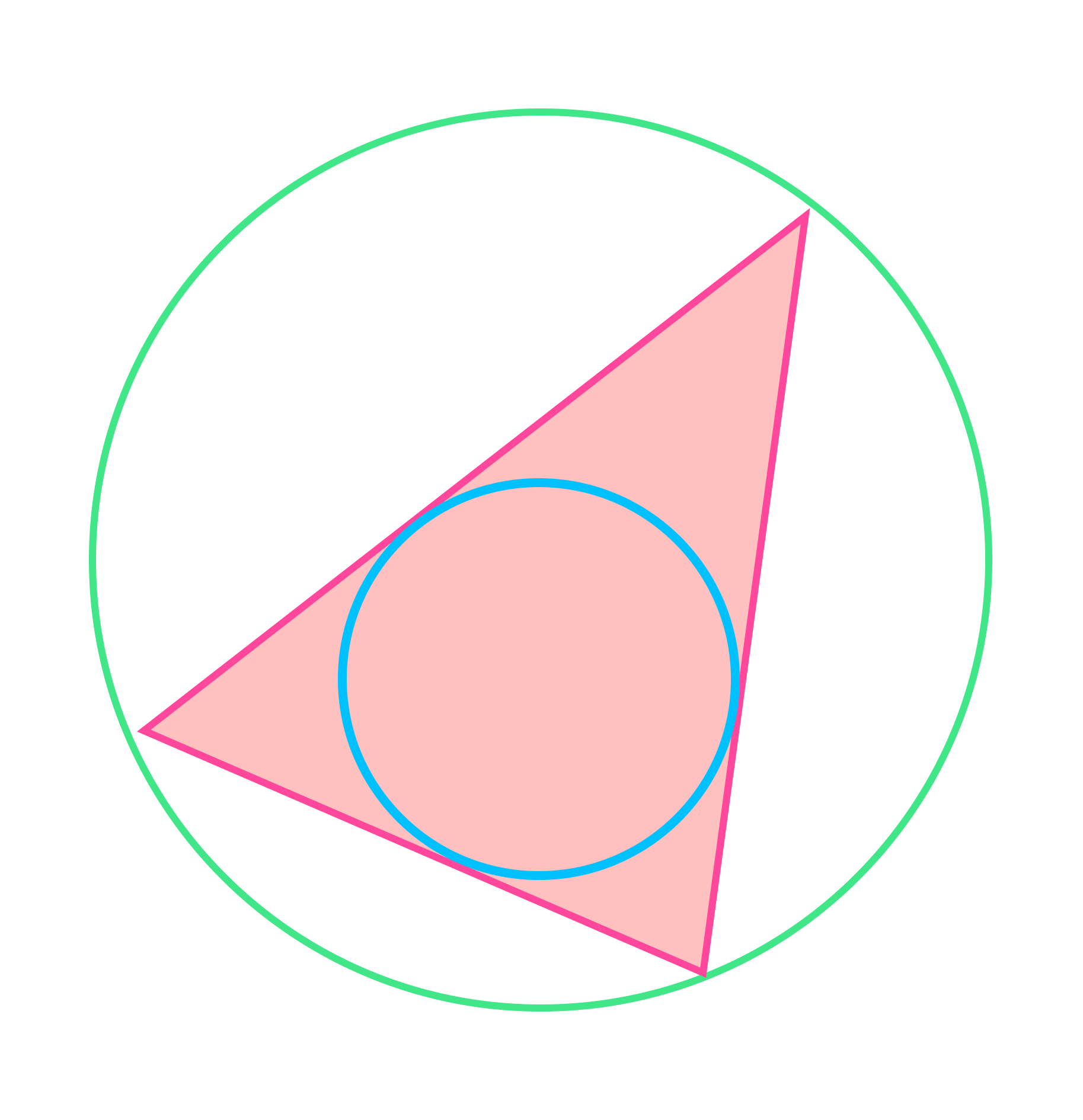
В любой треугольник можно вписать только одну окружность, и вокруг любого ее можно описать.
Все это верно только для треугольников. Не в любой четырехугольник можно вписать окружность, и не вокруг любого можно описать. Более подробно эту тему можно изучить на уроках математики: признаки, теоремы и правила.
Практическая сторона геометрии
Название «геометрия» переводится с греческого, как «гео» — земля и «метрео» — мерить. Изначально геометрию использовали для разметки земли и других работ с землей. Но, оказалось, что сфера ее влияния безгранична.
Чтобы понять, зачем нам нужны знания по геометрии, просто оглянитесь вокруг: геометрия окружает нас в предметах разных форм. Взять хотя бы круг: его используют в искусстве, строительстве, технике. То же самое и с другими фигурами: чтобы сконструировать автомобиль или айфон, сшить одежду или построить дом — не обойтись без геометрии.
А еще геометрия помогает научиться рассуждать логически, искать связи и противоречия — полезный навык в диджитал-мире, когда информация окружает нас повсюду.
Вот, в каких профессиях пригодится геометрия: архитектор, айтишник, дизайнер, инженер, конструктор, строитель, smm-менеджер, декоратор, летчик, водитель, художник, проектировщик, астроном, спортсмен, музыкант и другие.
Почему изучать геометрию просто: мы видим объемный мир каждый день и регулярно прикасаемся к предметам, строим планы, размышляем и считаем в уме. В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.
Почему изучать геометрию сложно: некоторые правила придется учить наизусть.
Чтобы понять геометрию, двигайтесь от простого к сложному. Многие теоремы могут показаться очевидными. Но эта видимость может быть верной только для одного рисунка. Невозможно нарисовать все ситуации, ведь их их бесконечное множество. Именно поэтому важно доказать истину, чтобы никогда не сомневаться в ней.