что такое ориентированный граф в информатике

Орграф

В математической теории графов и информатике граф — это совокупность объектов со связями между ними.

Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.

Многие структуры, представляющие практический интерес в математике и информатике, могут быть представлены графами. Например, строение Википедии можно смоделировать при помощи ориентированного графа (орграф), в котором вершины — это статьи, а дуги (ориентированные рёбра) — это связи, созданные гиперссылками (см. Тематическая карта).

Содержание

Определения

Теория графов не обладает устоявшейся терминологией. В различных статьях под одними и теми же терминами понимаются разные вещи. Приводимые ниже определения — наиболее часто встречаемые.

V (а значит и E ) обычно считаются конечными множествами. Многие хорошие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов. Это происходит потому, что ряд соображений становятся ложными в случае бесконечных множеств.

Вершины и рёбра графа называются также элементами графа, число вершин в графе | V | — порядком, число рёбер | E | — размером графа.

Два ребра называются смежными, если они имеют общую концевую вершину.

Два ребра называются кратными, если множества их концевых вершин совпадают.

Степенью degV вершины V называют количество рёбер, для которых она является концевой (при этом петли считают дважды).

Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.

Ориентированный граф

Дуга — это упорядоченная пара вершин (v, w), где вершину v называют началом, а w — концом дуги. Можно сказать, что дуга v 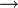w ведёт от вершины v к вершине w.

Смешанный граф

Понятно, что ориентированный и неориентированный графы являются частными случаями смешанного.

Прочие связанные определения

Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.

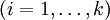
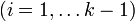
Ориентированным путём в орграфе называют конечную последовательность вершин v_i , для которой все пары (v_i,v_{i + 1}) являются (ориентированными) рёбрами.

Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Заметим, что если вершины u и v являются концами некоторого ребра, то согласно данному определению, последовательность (u,v,u) является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.

Путь (или цикл) называют простым, если ребра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются. Несложно видеть, что:

Бинарное отношение на множестве вершин графа, заданное как «существует путь из u в v », является отношением эквивалентности, и, следовательно, разбивает это множество на классы эквивалентности, называемые компонентами связности графа. Если у графа ровно одна компонента связности, то граф связный. На компоненте связности можно ввести понятие расстояния между вершинами как минимальную длину пути, соединяющего эти вершины.

Всякий максимальный связный подграф графа G называется связной компонентой (или просто компонентой) графа G. Слово «максимальный» означает максимальный относительно включения, то есть не содержащийся в связном подграфе с большим числом элементов

Ребро графа называется мостом, если его удаление увеличивает число компонент.

Дополнительные характеристики графов

Способы представления графа в информатике

Матрица смежности

Матрица смежности — таблица, где как столбцы, так и строки соответствуют вершинам графа. В каждой ячейке этой матрицы записывается число, определяющее наличие связи от вершины-строки к вершине-столбцу (либо наоборот).

Недостатком являются требования к памяти — очевидно, квадрат количества вершин.

Матрица инцидентности

Данный способ является самым ёмким (размер пропорционален | E | | V | ) и неудобным для хранения, но облегчает нахождение циклов в графе.

Список рёбер

Список рёбер — это тип представления графа в памяти, подразумевающий, что каждое ребро представляется двумя числами — номерами вершин этого ребра. Список рёбер более удобен для реализации различных алгоритмов на графах по сравнению с матрицей смежности.

Обобщение понятия графа

Простой граф является одномерным симплициальным комплексом.

Более абстрактно, граф можно задать как тройку , где V и E — некоторые множества (вершин и рёбер, соотв.), а — функция инцидентности (или инцидентор), сопоставляющая каждому ребру (упорядоченную или неупорядоченную) пару вершин u и v из V (его концов). Частными случаями этого понятия являются:

Под данное выше определение не подходят некоторые другие обобщения:

Литература

См. также

Ссылки

Популярные программы для визуализации графов

Источник

Графы: основы теории, алгоритмы поиска

Aug 22, 2020 · 6 min read

Возможно, вы уже знакомы с понятием спортивного программирования и знаете, что оно помогает развить навыки решения проблем и прокачать технические знания о структурах данных и алгоритмах.

Одной из важнейших составляющих спортивного программирования является изучение алгоритмов. В этой статье мы охватим большое количество алгоритмов, в том числе все алгоритмы на графах, знание которых понадобится вам для успешного решения задач из теории графов на соревнованиях по программированию. Конечно, одних теоретических знаний алгоритмов недостаточно, и вам придётся набить руку в решении практических задач на таких сайтах, как Codeforces. Настоящая же статья представит вам инструменты, необходимые для освоения важных графовых алгоритмов. Итак, приступим.

Что такое граф?

Г р афы, в понимании программистов, — это не те графики, которые мы изучали в школе. Это не столбиковые диаграммы или гистограммы.

С точки зрения компьютерных наук и дискретной математики, графы — это абстрактный способ представления типов отношений, например дорог, соединяющих города, и других видов сетей. Графы состоят из рёбер и вершин. Вершина — это точка на графе, а ребро — это то, что соединяет две точки на графе.

В условиях задач из теории графов на соревнованиях по программированию обычно говорится о таких вещах, как сети и решётки.

Вот список всех терминов, относящихся к теории графов, которые вам нужно знать:

Представление графов в коде

Для того, чтобы использовать алгоритмы на графах в коде, сначала нам нужно разобраться, как осуществляется представление графов в коде. Весь следующий код будет на C++, так как для спортивного программирования я предпочитаю именно этот язык за его скорость и встроенные функции, позволяющие упростить написание решений задач.

Будут показаны два способа представления графов: матрицы смежности и списки смежности. Больше вам пригодится представление графов в виде списка смежности.

Матрицы смежности

Матрица смежности представляет собой граф в виде двумерной матрицы с размерами V x V, где V — количество вершин графа. Матрицы смежности лучше всего применять, когда V² примерно равно E (числу рёбер), то есть когда граф плотный. Запись a_ij обозначает, сколько рёбер соединяют вершину i и вершину j.

Списки смежности

Другой распространенный способ представления графов в коде — списки смежности. Суть в том, что вы создаёте списки соседей для каждой вершины, а затем помещаете все эти списки в другой список. Их лучше всего применять, когда в графе небольшое количество рёбер, то есть когда граф разрежённый. Если у вас взвешенный граф, т.е. каждое ребро графа имеет какой-то вес, то в списке будут содержаться пары для рёбер (сосед, вес).

Поиск в глубину

Теперь, когда мы научились представлять графы в коде, можем приступить к изучению некоторых алгоритмов на графах! Начнём с поиска в глубину (DFS) и завершим поиском в ширину (BFS). Чтобы не загромождать статью, алгоритмы поиска пути не будут здесь рассматриваться (интересующиеся могут ознакомиться с алгоритмом поиска кратчайшего пути Беллмана-Форда).

Поиск в глубину — это один из базовых алгоритмов на графах. Он применяется для поиска расстояния от одной вершины до других вершин в графе. Это алгоритм обхода.

Поиск в глубину помечает каждую вершину в графе одной из двух меток: посещённая или не посещённая. Алгоритм помечает каждую вершину как посещённую, если удаётся избежать циклов. Он работает следующим образом:

Поиск в ширину

Поиск в ширину — ещё один алгоритм обхода графов. Вместе с алгоритмом поиска вглубь он составит большую часть увлекательных соревнований по программированию, по крайней мере, тех из них, что относятся к графам.

Поиск в ширину тоже помещает каждую вершину в графе в одну из двух категорий: посещённых или непосещённых. И цель у обоих алгоритмов одна и та же: помечать каждую вершину в графе как посещённую, если удаётся избежать циклов. Вот как работает алгоритм поиска в ширину:

Как видите, алгоритм поиска в ширину очень похож на алгоритм поиска в глубину. Однако вместо того, чтобы спускаться вниз по ветви графа или дерева, как это делает алгоритм поиска в глубину, алгоритм поиска в ширину проходит каждый уровень.

Заключение

Освоив теоретическую часть, касающуюся двух самых важных алгоритмов обхода на графах, вам остаётся только практиковаться, чтобы использовать эти алгоритмы в соревнованиях по программированию. Я бы порекомендовал для начала Codeforces: решайте задачи, помеченные тегами bfs и dfs с рейтингом до 1400. Когда почувствуете, что справляетесь с ними, увеличьте сложность.

Отработка навыков решения алгоритмических задач, особенно алгоритмов на графах, поможет вам побеждать на соревнованиях по программированию и успешно проходить технические собеседования. Вперёд — к успехам!

Источник

Теория графов. Основные понятия и виды графов.

Перед тем как начать изучение непосредственно алгоритмов, необходимо обладать базовыми знаниями касательно самих графов, понимать, как они представляются в компьютере. Здесь не будут подробно описаны все аспекты теории графов (этого и не требуется), но только те, незнание которых заметно усложнит усвоение данной области программирования.

Несколько примеров дадут немного поверхностного представления о графе. Так типичным графом является схема метро или какой-либо другой маршрут. В частности программисту знакома компьютерная сеть, также являющаяся графом. Общее здесь это наличие точек, соединенных линиями. Так в компьютерной сети точки – это отдельные серверы, а линии – различные виды электрических сигналов. В метрополитене первое – станции, второе – туннели, проложенные между ними. В теории графов точки именуется вершинами (узлами), а линии – ребрами (дугами). Таким образом, граф – это совокупность вершин, соединённых ребрами.

Математика оперирует не содержанием вещей, а их структурой, абстрагируя ее из всего того, что дано как целое. Пользуясь именно этим приемом, мы можем заключать о каких-либо объектах как о графах. А поскольку теория графов это часть математики, то для нее нет абсолютно никакого значения, что в принципе представляет собой объект; важно лишь то, является ли он графом, т. е. обладает ли обязательными для графов свойствами. Поэтому, прежде чем привести примеры, мы выделяем в рассматриваемом объекте лишь то, что как нам кажется, позволит показать аналогию, отыскиваем общее.

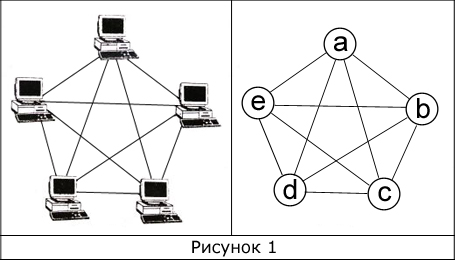
Вернемся к компьютерной сети. Она обладает определенной топологией, и может быть условно изображена в виде некоторого числа компьютеров и путей их соединяющих. На рисунке ниже в качестве примера показана полносвязная топология.

Это по сути граф. Пять компьютеров являются вершинами, а соединения (пути передачи сигналов) между ними – ребрами. Заменив компьютеры вершинами, мы получим математический объект – граф, который имеет 10 ребер и 5 вершин. Пронумеровать вершины можно произвольным образом, а не обязательно так, как это сделано на рисунке. Стоит отметить, что в данном примере не используется ни одной петли, то есть такого ребра, которое выходит из вершины и сразу же входит в нее, но петли могут встречаться в задачах.

Вот некоторые важные обозначения, используемые в теории графов:

В нашем случае (рис. 1) |V|=5, |E|=10;

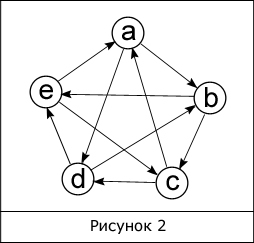
Когда из любой вершины доступна любая другая вершина, то такой граф называется неориентированным связным графом (рис. 1). Если же граф связный, но это условие не выполняется, тогда такой граф называется ориентированным или орграфом (рис. 2).

В ориентированных и неориентированных графах имеется понятие степени вершины. Степень вершины – это количество ребер, соединяющих ее с другими вершинами. Сумма всех степеней графа равна удвоенному количеству всех его ребер. Для рисунка 2 сумма всех степеней равна 20.

В орграфе, в отличие от неориентированного графа, имеется возможность двигаться из вершины h в вершину s без промежуточных вершин, лишь тогда когда ребро выходит из h и входит в s, но не наоборот.

Ориентированные графы имеют следующую форму записи:

G=(V, A), где V – вершины, A – направленные ребра.

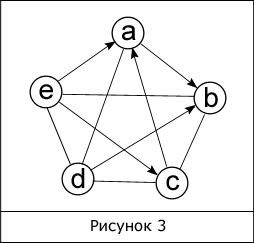
Третий тип графов – смешанные графы (рис. 3). Они имеют как направленные ребра, так и ненаправленные. Формально смешанный граф записывается так: G=(V, E, A), где каждая из букв в скобках обозначает тоже, что ей приписывалось ранее.

В графе на рисунке 3 одни дуги направленные [(e, a), (e, c), (a, b), (c, a), (d, b)], другие – ненаправленные [(e, d), (e, b), (d, c)…].

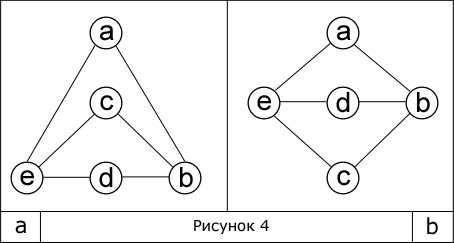
Два или более графов на первый взгляд могут показаться разными по своей структуре, что возникает вследствие различного их изображения. Но это не всегда так. Возьмем два графа (рис. 4).

Они эквивалентны друг другу, ведь не изменяя структуру одного графа можно построить другой. Такие графы называются изоморфными, т. е. обладающими тем свойством, что какая-либо вершина с определенным числом ребер в одном графе имеет тождественную вершину в другом. На рисунке 4 изображены два изоморфных графа.

Когда каждому ребру графа поставлено в соответствие некоторое значение, называемое весом ребра, тогда такой граф взвешенный. В разных задачах в качестве веса могут выступать различные виды измерений, например длины, цены маршруты и т. п. В графическом представлении графа весовые значения указываются, как правило, рядом с ребрами.

В любом из рассмотренных нами графов имеется возможность выделить путь и, причем не один. Путь – это последовательность вершин, каждая из которых соединена с последующей посредством ребра. Если первая и последняя вершины совпадают, то такой путь называется циклом. Длина пути определяется количеством составляющих его ребер. Например, на рисунке 4.а путем служит последовательность [(e), (a), (b), (c)]. Этот путь является подграфом, так как к нему применимо определение последнего, а именно: граф G’=(V’, E’) является подграфом графа G=(V, E), только тогда когда V’ и E’ принадлежат V, E.

Способы представления графов.

Граф, как и большинство других математических объектов, может быть представлен на компьютере (сохранен в его памяти). Существуют несколько способов его интерпретации, вот наиболее известные из них:

Использование двух первых методов предполагает хранение графа в виде двумерного массива (матрицы). Причем размеры этих массивов, зависят от количества вершин и/или ребер в конкретном графе. Так размер матрицы смежности n×n, где n – число вершин, а матрицы инцидентности n×m, n – число вершин, m – число ребер в графе.

Источник

Учитель информатики

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

Графы

Информатика. Учебник для 9 класса (по учебнику К. Ю. Полякова, Е.А. Еремина, базовый уровень)

§17. Графы.

Что такое граф?

Ключевые слова:

Давайте подумаем, как можно наглядно представить такую информацию:

От пос. Васюки три дороги идут в Солнцево, Грибное и Ягодное. Между Солнцевом и Грибным и между Грибным и Ягодным также есть дороги. Кроме того, есть дорога, которая идет из Грибного в лес и возвращается обратно в Грибное.
Нарисуйте в тетради схему дорог по этому описанию.

Можно, например, нарисовать такую схему (рис. 3.17, а).

Рис. 3.17

В информатике для исследования таких схем используют графы.

Граф — это набор вершин (узлов) и связей между ними — рёбер.

Граф, соответствующий нашей схеме дорог, показан на рис. 3.17, б, для краткости населённые пункты обозначены латинскими буквами.

Матрица смежности графа

Для хранения информации об узлах и связях показанного выше графа можно использовать таблицу такого вида (рис. 3.18).

Рис. 3.18

Единица на пересечении строки А и столбца В означает, что между вершинами А и В есть связь. Ноль указывает на то, что связи нет. Такая таблица называется матрицей смежности. Она симметрична относительно главной диагонали (см. закрашенные клетки в таблице).

Исследуйте матрицу смежности и сравните её с графом на рис. 3.17, б. Что означает единица на пересечении столбца С и строки С?

В этом графе есть петля — ребро, которое начинается и заканчивается в одной и той же вершине.

Степенью вершины называют количество рёбер, с которыми связана вершина. При этом петля считается дважды (с вершиной связаны оба конца ребра!).

Подсчитайте по матрице смежности, сколько ребёр в графе. Определите степени всех вершин. Как вы рассуждали?

Строго говоря, граф — это математический объект, а не рисунок. Конечно, его можно нарисовать на плоскости (например, как на рис. 3.17, б), но матрица смежности не даёт никакой информации о том, как именно располагать вершины друг относительно друга. Для таблицы, приведённой выше, возможны, например, такие варианты (рис. 3.19).

Рис. 3.19

Нарисуйте по матрице смежности (рис. 3.20) два разных изображения графа.

Рис. 3.20

Граф имеет 4 вершины, причём каждая вершина связана рёбрами со всеми остальными. Нарисуйте этот граф. Сколько всего рёбер в этом графе?

Граф имеет N вершин, причём каждая вершина связана рёбрами со всеми остальными. Сколько всего рёбер в этом графе?

Граф имеет 4 ребра. Чему равна сумма степеней вершин в этом графе? Зависит ли она от количества вершин?

Граф имеет N рёбер. Чему равна сумма степеней вершин в этом графе?

Попробуйте нарисовать граф с пятью вершинами, где все вершины имеют степень 3. Получилось ли у вас? Почему?

Связный граф

В графе на рис. 3.17, б все вершины связаны: между любой парой вершин существует путь — последовательность вершин, в которой каждая следующая связана ребром с предыдущей. Такой граф называется связным.

Связный граф — это граф, между любыми вершинами которого существует путь.

Теперь представьте себе, что дороги Васюки-Солнцево, Васю- ки-Грибное и Грибное-Ягодное завалило снегом (или размыло дождём) так, что по ним ни пройти, ни проехать (рис. 3.21).

Рис. 3.21

Эту схему тоже можно считать графом (она соответствует определению), но в таком графе есть две несвязанные части, каждая из которых — связный граф. Такие части называют компонентами связности.

Постройте матрицу смежности графа, изображённого на рис. 3.21.

Граф имеет 4 вершины и две компоненты связности. Какое наибольшее количество рёбер может быть в этом графе, если в нём нет петель? Нарисуйте этот граф.

Вспоминая материал предыдущего параграфа, можно сделать вывод, что дерево — это частный случай связного графа. Но у него есть одно важное свойство — в дереве нет замкнутых путей — циклов, т. е. путей, которые начинаются и заканчиваются в одной и той же вершине.

Найдите все циклы в графе на рис. 3.17.

Дерево — это связный граф, в котором нет циклов.

Взвешенный граф

Если в нашем примере нас заинтересует не только наличие дорог между посёлками, но ещё и расстояния между ними, каждой связи нужно сопоставить число — вес ребра (рис. 3.22).

Рис. 3.22

Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра.

Весом может быть не только расстояние, но и, например, стоимость проезда или другая величина.

Рис. 3.23

Так же как и матрица смежности, весовая матрица симметрична относительно диагонали.

Что означают пустые ячейки в весовой матрице?

Как по весовой матрице сразу определить, сколько рёбер в графе?

Определите по весовой матрице (рис. 3.24) длины путей ADBEC, ABDCE, DEBAC. Как вы рассуждали?

Рис. 3.24

Оптимальный путь в графе

Для того чтобы определить оптимальный (наилучший) путь между двумя вершинами графа, нужно ввести какой-то числовой показатель, по которому можно сравнивать пути — определять, какой из них лучше. Обычно для оценки пути используют сумму весов ребёр, входящих в этот путь. Например, при поиске кратчайшего пути чем меньше это значение, тем лучше.

Какие показатели вы используете в жизни для определения оптимального пути? Всегда ли самый короткий путь — самый лучший?

Если в графе немного узлов, по весовой матрице можно легко определить оптимальный путь из одной вершины в другую простым перебором вариантов. Рассмотрим граф, заданный весовой матрицей на рис. 3.25 (числа определяют стоимость поездки между соседними пунктами).

Рис. 3.25

Найдём наилучший путь из А в В — такой, при котором общая стоимость поездки минимальная.

Для решения задачи будем строить дерево перебора вариантов. Видим, что из пункта А напрямую

Рис. 3.26

Числа около рёбер обозначают стоимость поездки по этому участку, а индексы у названий узлов показывают общую стоимость проезда в данный узел из узла А. Теперь разберём варианты дальнейшего движения из узла С I tM lt;pb р (рис. 3.27).

Рис. 3.27

Почему, на ваш взгляд, на схеме не показана возможность движения из С в А?

Видим, что из С сразу можно попасть в В, стоимость проезда в этом случае равна 7.

Почему нельзя на этом остановиться, ведь путь из А в В найден?

Проверяя пути через узел В, выясняем, что можно сократить стоимость до 6 (рис. 3.28)

Рис. 3.28

Нужно ли исследовать дальше путь, содержащий цепочку ACED? Сравните стоимость этого пути и стоимость уже найденного пути из А в В.

Аналогично строим вторую часть схемы (рис. 3.29).

Рис. 3.29

Таким образом, оптимальный (наилучший) путь — ADEB, его стоимость — 3.

Нужно ли проверять пути ACED и ADEC, не дошедшие до узла В? Могут ли они улучшить результат?

Конечно, для более сложных графов метод перебора работает очень долго, поэтому используются более совершенные (но значительно более сложные) методы.

Ориентированный граф

Наверное, вы заметили, что при изображении деревьев, которые описывают иерархию (подчинение), мы ставили стрелки от верхних уровней к нижним. Это означает, что для каждого ребра указывается направление, и двигаться можно только по стрелкам, но не наоборот.

Ориентированный граф (орграф) — это граф, в котором каждое ребро имеет направление.

Орграф может служить, например, моделью системы дорог с односторонним движением. Матрица смежности и весовая матрица для орграфа уже не обязательно будут симметричными.

На схеме на рис. 3.30 всего две дороги с двусторонним движением, по остальным можно ехать только в одну сторону.

Рис. 3.30

Рёбра в орграфе называют дугами. Дуга, в отличие от ребра, имеет начало и конец.

Нарисуйте граф по весовой матрице, показанной на рис. 3.31. С помощью дерева перебора найдите все возможные пути из вершины А в вершину Е, не проходящие дважды через одну и ту же вершину, и стоимости проезда по каждому из этих путей. Определите оптимальный путь из вершины А в вершину Е.

Рис. 3.31

Количество путей

Определим количество возможных путей из вершины А в вершину К для ориентированного графа, показанного на рис. 3.32.

Рис. 3.32

Так как граф ориентированный, переходить в другую вершину можно только по стрелкам.

В графе на рис. 3.32 есть одна начальная вершина А, из которой дуги только выходят. Такая вершина называется истоком. Вершина, в которую дуги только входят (и ни одна не выходит), называется конечной вершиной или стоком. В нашем графе сток — это вершина К.

По весовой матрице на рис. 3.31 найдите исток и сток в графе. Как вы рассуждали?

Будем двигаться по стрелкам от начальной вершины А. Около каждой вершины запишем количество возможных путей из вершины А в эту вершину. В вершину А существует единственный путь — пустой (никуда не ехать). Найдём все вершины, в которые можно приехать только из А: это вершины Б и Г, записываем около них количество путей 1 (рис. 3.33).

Рис. 3.33

Теперь ищем вершины, в которые можно попасть только из уже отмеченных вершин. Например, в вершину В есть один путь из А напрямую, а также по одному пути через Б и Г (так как эти вершины отмечены числом 1). Общее количество путей из А в Б равно сумме отметок предыдущих вершин: для вершины В получаем 3 пути. В вершину Ж можно попасть только из Г, поэтому число путей в Г и Ж совпадает (рис. 3.34).

Рис. 3.34

В вершину Д идёт один путь через Б и три пути через В, поэтому общее число путей — 4. Аналогично получаем 4 пути в вершину Е: 3 пути через В и один через Ж (рис. 3.35).

Рис. 3.35

Далее находим один путь из А в И (только через Ж) и 4 пути из А в 3 (все через Д). В конечную вершину К можно приехать через вершины Д (4 пути), 3 (4 пути), Е (4 пути) и И (1 путь), таким образом, общее количество различных путей равно 13 (рис. 3.36).

Рис. 3.36

Выводы

• Граф — это набор вершин (узлов) и связей между ними — рёбер.
• Матрица смежности — это таблица, в которой единица на пересечении строки и столбца обозначает ребро между соответствующими вершинами, а ноль — отсутствие ребра.
• Связный граф — это граф, между любыми вершинами которого существует путь.
• Цикл — это замкнутый путь в графе.
• Дерево — это связный граф, в котором нет циклов.
• Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра. Взвешенный граф описывается весовой матрицей.
• Ориентированный граф (орграф) — это граф, в котором каждое ребро имеет направление. Рёбра орграфа называют дугами. Матрица смежности и весовая матрица орграфа могут быть несимметричными.

Нарисуйте в тетради интеллект-карту этого параграфа.

Вопросы и задания

1. Можно ли сказать, что лес (множество деревьев) — это граф? Почему?
2. Как по матрице смежности определить, есть ли петли в графе?
3. Как по весовой матрице определить длину пути в графе?
4. Когда для представления данных используются орграфы? Приведите примеры.
5. Выполните по указанию учителя задания в рабочей тетради.

Подготовьте сообщение

а) «Задача о Кёнигсбергских мостах»
б) «Решение логических задач с помощью графов»

Источник