что такое опорный план в симплекс методе
Лекция 6
Алгоритм симплекс метода
Симплекс метод (метод последовательного улучшения плана)
Метод предназначен для решения общей задачи линейного программирования.
Пусть имеем следующую задачу:
с системой ограничений следующего вида:
Целевую функцию можно выразить через небазисные переменные:
Вектор с такими компонентами представляет собой угловую точку многогранника решений (допустимую) при условии, что (опорный план).
Теперь необходимо перейти к другой угловой точке с меньшим значением целевой функции. Для этого следует выбрать некоторую небазисную переменную и некоторую базисную так, чтобы после того, как мы “поменяем их местами”, значение целевой функции уменьшилось. Такой направленный перебор в конце концов приведет нас к решению задачи.
Пример 1.
Выберем в качестве базисных следующие переменные < x1, x2, x3> и разрешим систему относительно этих переменных. Система ограничений примет следующий вид:
Значение целевой функции можно уменьшить за счет увеличения x5. При увеличении x5 величина x1 также увеличивается, а x2 и x3 – уменьшаются. Причем величина x2 раньше может стать отрицательной. Поэтому, вводя в базис переменную x5, одновременно x2 исключаем из базиса. В результате после очевидных преобразований получим следующие выражения для новой системы базисных переменных и целевой функции:
Целевую функцию можно уменьшить за счет увеличения x4. Увеличение x4 приводит к уменьшению только x3. Поэтому вводим в базис переменную x4, а x3 исключаем из базиса. В результате получим следующие выражения для новой системы базисных переменных и целевой функции:
Пример 2.
Пусть имеем задачу
Теперь вводим в базис переменную x1, a x4 исключаем из базиса. В результате получим следующие выражения для базисных переменных и целевой функции:
Теперь можно заметить, что при увеличении x2 значения переменных x1 и x3 также возрастают, то есть при в допустимой области (задача не имеет решения).
Замечание
В процессе поиска допустимого плана может быть выявлена противоречивость системы ограничений.
Алгоритм симплекс метода
Проиллюстрируем алгоритм на рассмотренном ранее примере:
В случае базисных переменных < x1, x2, x3>начальная симплексная таблица для данного примера будет выглядеть следующим образом:
| — x4 | — x5 | 1 | |
| x1= | 1 | -2 | 1 |
| x2= | -2 | 1 | 2 |
| x3= | 3 | 1 | 3 |
| = | -1 | 1 | 0 |
Она уже соответствует опорному плану (столбец свободных членов).
Построение оптимального плана.
Выбор разрешающего элемента. Если при поиске минимума в строке целевой функции есть коэффициенты больше нуля, то выбираем столбец с положительным коэффициентом в строке целевой функции в качестве разрешающего. Пусть это столбец с номером l.
Для выбора разрешающей строки (разрешающего элемента) среди положительных коэффициентов разрешающего столбца выбираем тот (строку), для которого отношение коэффициента в столбце свободных членов к коэффициенту в разрешающем столбце минимально:
arl – разрешающий (направляющий) элемент, строка r – разрешающая.
Для перехода к следующей симплексной таблице (следующему опорному плану с меньшим значением целевой функции) делается шаг модифицированного жорданова исключения с разрешающим элементом arl.
Если в разрешающем столбце нет положительных коэффициентов, то целевая функция неограничена снизу (при максимизации – неограничена сверху).
Шаг модифицированного жорданова исключения над симплексной таблицей. На месте разрешающего элемента ставится 1 и делится на разрешающий элемент.
Остальные элементы разрешающего столбца меняют знак на противоположный и делятся на разрешающий элемент.
Остальные элементы разрешающей строки делятся на разрешающий элемент.
Построение опорного плана.
Пусть необходимо решить задачу:
Введем дополнительные переменные, чтобы преобразовать ограничения-неравенства к равенствам. В ограничениях-равенствах дополнительные переменные должны быть нулевыми. Тогда система ограничений принимает вид:
В качестве базисных переменных будем брать систему дополнительно введенных переменных. Тогда симплексная таблица для преобразованной задачи будет иметь следующий вид:
| — x1 | — x2 | …. | — xs | .… | — xn | 1 | |
| 0 | a1,1 | a1,2 | …. | a1,s | …. | a1,n | b1 |
| …. | …. | …. | …. | …. | …. | …. | …. |
| 0 | am,1 | am,2 | …. | am,s | …. | am,n | bm |
| xm+1 | am+1,1 | am+1,2 | …. | am+1,s | …. | am+1,n | bm+1 |
| …. | …. | …. | …. | …. | …. | …. | …. |
| xm+p | am+p,1 | am+p,2 | …. | am+p,s | …. | am+p,n | bm+p |
| — c1 | — c2 | …. | — cs | …. | — cn | 0 |
Вырожденность в задачах линейного программирования
Если задача линейного программирования оказывается вырожденной, то при плохом выборе вектора условий, выводимого из базиса, может возникнуть бесконечное движение по базисам одного и того же опорного плана. Так называемое, явление зацикливания. Хотя в практических задачах линейного программирования зацикливание явление крайне редкое, возможность его не исключена.
Один из приемов борьбы с вырожденностью состоит в преобразовании задачи путем «незначительного» изменения вектора правых частей системы ограничений на величины εi, таким образом, чтобы задача стала невырожденной, и, в то же время, чтобы это изменение не повлияло реально на оптимальный план задачи.
Чаще реализуемые алгоритмы включают в себя некоторые простые правила, снижающие вероятность возникновения зацикливания или его преодоления.
Практически правилом надо пользоваться, если зацикливание уже обнаружено.
Поиск первоначального опорного плана
Запишем задачу в симплекс-таблицу (табл. 1).
Таблица 2
| базисные | —х4 | —х2 | —х6 | свободные |
| х1 | -1/3 | 2/3 | 1/3 | 7 |
| х5 | -5/6 | 1/6 | 1/3 | ½ |
| х3 | 1/6 | 1/6 | -2/3 | 5/2 |
| F | 5 | 5 | 0 | 165 |
Полученный базисный план х* = (х1, х2, х3, х4, х5, х6) = (7, 0, 5/2, 0, 1/2, 0) является допустимым и, к тому же, оказывается оптимальным, т.к. в индексной строке нет отрицательных элементов. Оптимальное значение целевой функции равно F* = 165. Действительно,
F = 20х1 + 20х2 + 10х3 = 20 · 7 + 0 + 10· 5 /2 = 140 + 25 = 165.
В этой задаче не пришлось улучшать найденный первоначальный опорный план, т.к. он оказался оптимальным. Иначе, мы должны были вернуться к III этапу.
Решение задачи о плане симплекс-методом
Целевая функция выражает собой общую суммарную прибыль, полученную от реализации всей плановой продукции, а каждое из неравенств выражает затраты определенного вида продукции. Понятно, что затраты не должны превышать запасов сырья.
Приведем задачу к канонической форме и к специальному виду, введя дополнительные переменные х 5, х 6, х 7 в каждое из неравенств.
Очевидно, что, если первого ресурса необходимо для производства плановой продукции 5х1 + 0,4х2 + 2х3 + 0,5х4, то х5 обозначает просто излишки первого ресурса как разность между имеющимся запасом и требуемым для производства. Аналогично х6 и х7. Итак, дополнительные перемены задачи ЛП обозначают излишки сырья, времени, других ресурсов, остающихся в производстве данного оптимального плана.
III этап. Улучшение опорного плана. Выберем в качестве разрешающего столбца четвертый, но могли бы выбрать и второй, т.к. в обоих (-5). Остановившись на четвертом, выберем в качестве разрешающего элемента 1, т.к. именно на нем достигается минимум соотношений 
В качестве разрешающего элемента выбираем 5, т.к. 
Пересчитываем еще раз таблицу. Заметим, что пересчет удобно начинать с индексной строки, т.к. если в ней все элементы неотрицательны, то план оптимален, и чтобы его выписать, достаточно пересчитать столбец свободных членов, нет необходимости вычислять «внутренность» таблицы (табл. 6).
700
План оптимален, т.к. в индексной строке нет отрицательных элементов, выписываем его.
Подробный разбор симплекс-метода
Пролог
Недавно появилась необходимость создать с нуля программу, реализующую алгоритм симплекс-метода. Но в ходе решения я столкнулся с проблемой: в интернете не так уж много ресурсов, на которых можно посмотреть подробный теоретический разбор алгоритма (его обоснование: почему мы делаем те или иные шаги) и советы по практической реализации — непосредственно, алгоритм. Тогда я дал себе обещание — как только завершу задачу, напишу свой пост на эту тему. Об этом, собственно, и поговорим.
Замечание. Пост будет написан достаточно формальным языком, но будет снабжен комментариями, которые должны внести некоторую ясность. Такой формат позволит сохранить научный подход и при этом, возможно, поможет некоторым в изучении данного вопроса.
§1. Постановка задачи линейного программирования
Определение: Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств.
Общая задача линейного программирования (далее – ЛП) имеет вид:
§2. Каноническая форма задачи ЛП
Каноническая форма задачи ЛП:
Замечание: Любая задача ЛП сводится к канонической.
Алгоритм перехода от произвольной задачи ЛП к канонической форме:
Замечание: ≥0.
§3. Угловые точки. Базисные/свободные переменные. Базисные решения
Определение: Точка называется угловой точкой, если представление
возможно только при
.
Иными словами, невозможно найти две точки в области, интервал проходящий через которые содержит (т.е.
– не внутренняя точка).
Графический способ решения задачи ЛП показывает, что нахождение оптимального решения ассоциируется с угловой точкой. Это является основной концепцией при разработке симплекс-метода.
Определение: Пусть есть система m уравнений и n неизвестных (m
11. Построение опорных планов в симплексном методе решения здп.
Симплексный метод – это метод целенаправленного перебора опорных решений задачи. Этот метод позволяет за конечное число шагов расчёта найти оптимальное решение либо установить, что решения не существует. Содержание метода:
1)указать способ нахождения начального опорного решения;
2)указать способ перехода то одного опорного решения к другому, на котором значение целевой функции ближе к оптимальному;
3)задать критерий, который позволяет прекратить перебор решений на оптималном решении или сделать заключение об отсутствии решения.
Пусть имеется задача в канонической форме:
Любую задачу можно представить в векторной форме.
АХ=В, где 
Решение, удовлетворяющее всем ограничениям и условиям неотрицательности, называется допустимым. Множество всех допустимых решений образуют область допустимых решений (ОДР). Допустимое решение, доставляющее мин. или макс. целевой функции называется оптимальным решением. Матрица А, составленная из коэффициентов при неизвестных называется матрицей условий.
Вектор столбец А0= 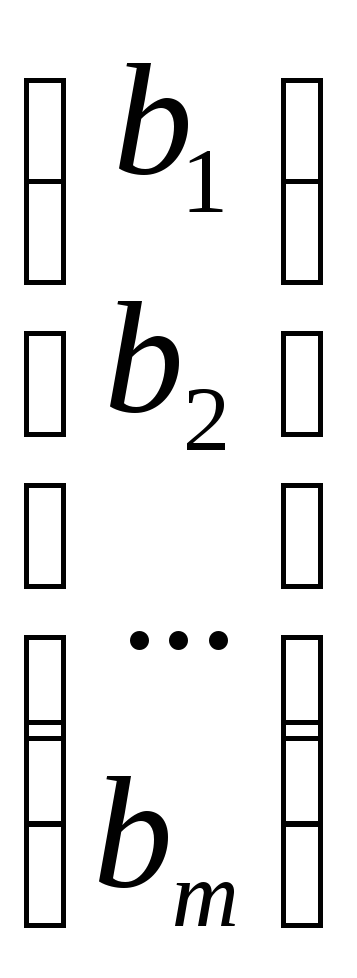
Замечание. Нахождение оптимального решения может вызвать затруднение с перебором всех опорных решений когда задача имеет бесконечное множество решений или решение отсутствует. По этому вводят специальный параметр θ.
Построение начального опорного решения. Необходимо в каждом уравнении системы найти базисную переменную (которая входит только в одно уравнение с коэффициентом +1). Обозначаю базисную переменную хiб. х1б – базисная переменная первого уравнения и т.д. Составляется первая симплекс-таблица следующим образом.
Симплексный метод решения ЗЛП
Задачи динамического программирования
Распределить 5 однородных партий товара между тремя рынками так, чтобы получить максимальный доход от их продажи. Доход от продажи на каждом рынке G(X) зависит от количества реализованных партий товара Х и представлен в таблице.
| Объем товара Х (в партиях) | Доход G(X) | ||
| 1 | 2 | 3 | |
| 0 | 0 | 0 | 0 |
| 1 | 28 | 30 | 32 |
| 2 | 41 | 42 | 45 |
| 3 | 50 | 55 | 48 |
| 4 | 62 | 64 | 60 |
| 5 | 76 | 76 | 72 |
Экстремальное решение достигается на границе области допустимых решений в одной из вершин угловых точек многоугольника, либо на отрезке между двумя соседними угловыми точками.
Суть симплекс-метода. Движение к точке оптимума осуществляется путем перехода от одной угловой точки к соседней, которая ближе и быстрее приближает к Xопт. Такую схему перебора точек, называемую симплекс-метод, предложил Р. Данцигом.
Угловые точки характеризуются m базисными переменными, поэтому переход от одной угловой точки к соседней возможно осуществить сменой в базисе только одной базисной переменной на переменную из небазиса.
Реализация симплекс-метода в силу различных особенностей и постановок задач ЛП имеет различные модификации.
Построение симплекс-таблиц продолжается до тех пор, пока не будет получено оптимальное решение.
Как с помощью симплекс-таблицы определить, что решение задачи линейного программирования является оптимальным?
Если последняя строка (значения целевой функции) не содержит отрицательных элементов, следовательно, найдет оптимальный план.
Если задано условие «Необходимо, чтобы сырье III вида было израсходовано полностью», то соответствующее условие представляет собой равенство.
Аналитическое введение в симплекс-метод
Например, пусть дана система
Совокупность переменных x1 и x2 образует базис: Б (x1, x2). Если x3 = 0, то полученное частное решение (5, 11, 0) называется базисным решением, соответствующим базису Б (x1, x2).
Базисное решение, соответствующее базису Б (x1, x3), таково: (-19/5; 0; 11/5).
Если теперь от базиса Б (x1, x3) нам захочется перейти к базису Б (x2, x3), то
На этом примере очень наглядно продемонстрирована идея метода: постепенно переходя от базиса к базису, при этом всегда обращая внимание на значения целевой функции, которые должны улучшиться, мы приходим к такому базису, в котором значение целевой функции улучшить нельзя, оно оптимально. Заметим, что базисов конечное число, поэтому количество шагов, совершаемых нами до того нужного базиса, конечно.
