что такое однородное дифференциальное уравнение

Источник

Однородное дифференциальное уравнение

Обыкновенное уравнение первого порядка называется однородным относительно x и y, если функция является однородной степени 0:

.

Однородную функцию можно представить как функцию от :

.

Используем подстановку , а затем воспользуемся правилом произведения : . Тогда, дифференциальное уравнение сводится к уравнению с разделяющимися переменными:

+ = 0″ border=»0″ />.

Дифференциальное уравнение является однородным, если оно не содержит свободного члена — слагаемого, не зависящего от неизвестной функции. Так, можно говорить, что уравнение — однородно, если .

В случае, если , говорят о неоднородном дифференциальном уравнении.

Именно для решения линейных однородных диф. уравнений была построена целая теория, чему способствовало выполнение у них принципа суперпозиции.

См. также

Полезное

Смотреть что такое «Однородное дифференциальное уравнение» в других словарях:

Дифференциальное уравнение — Дифференциальное уравнение уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию,… … Википедия

Дифференциальное уравнение Бернулли — У этого термина существуют и другие значения, см. Уравнение Бернулли. Обыкновенное дифференциальное уравнение вида: называется уравнением Бернулли (при или получаем неоднородное или однородное линейное уравнение). При является частным случаем… … Википедия

Неоднородное дифференциальное уравнение — Неоднородное дифференциальное уравнение дифференциальное уравнение (обыкновенное или в частных производных), которое содержит не равный тождественно нулю свободный член слагаемое, не зависящее от неизвестных функций. Обычно имеет те… … Википедия

Линейное дифференциальное уравнение с постоянными коэффициентами — Линейное дифференциальное уравнение с постоянными коэффициентами обыкновенное дифференциальное уравнение вида: где искомая функция, её тая производная, фиксированные числа … Википедия

ЛИНЕЙНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ — обыкновенное уравнение вида где x(t) искомая функция, заданные действительные числа, f(t) заданная действительная функция. Соответствующее (1) однородное уравнение интегрируется следующим образом. Пусть все различные корни характеристич.… … Математическая энциклопедия

Однородное уравнение — Однородным уравнением n й степени, называется уравнение вида: Такое уравнение после исключения отдельно рассматриваемого случая и деления уравнения на сводится с помощью замены к алгебраическому уравнению … Википедия

Уравнение Коши — Эйлера — В математике ( дифференциальных уравнениях), уравнение Коши Эйлера (Эйлера Коши) является частным случаем линейного дифференциального уравнения (см. линейное дифференциальное уравнение), приводимым к линейному дифференциальному уравнению с… … Википедия

Уравнение диффузии — Механика сплошных сред … Википедия

Источник

Виды дифференциальных уравнений

Существует целый ряд задач, в которых установить прямую связь между величинами, применяемыми для описания процесса, не получается. Единственное, что можно сделать, это получить равенство, запись которого включает производные исследуемых функций, и решить его. Решение дифференциального уравнения позволяет установить непосредственную связь между величинами.

В этом разделе мы займемся разбором решений дифференциальных уравнений, неизвестная функция в которых является функцией одной переменной. Мы построили теоретическую часть таким образом, чтобы даже человек с нулевым представлением о дифференциальных уравнениях мог без труда получить необходимые знания и справиться с приведенными задачами.

Если какие-то термины окажутся для вас новыми, обратитесь к разделу «Определения и понятия теории дифференциальных уравнений». А тем временем перейдем к рассмотрению вопроса о видах дифференциальных уравнений.

Для каждого из видов дифференциальных уравнений применяется свой метод решения. В этом разделе мы рассмотрим все эти методы, приведем примеры с подробными разборами решения. После ознакомления с темой вам необходимо будет определять вид дифференциального уравнения и выбирать наиболее подходящий из методов решения поставленной задачи.

Возможно, прежде чем приступить к решению дифференциальных уравнений, вам придется освежить в памяти такие темы как «Методы интегрирования» и «Неопределенные интегралы».

Дифференциальные уравнения первого порядка

Простейшие дифференциальные уравнения первого порядка вида y ‘ = f ( x )

Начнем с примеров таких уравнений.

Приведем примеры подобных дифференциальных уравнений:

Дифференциальные уравнения с разделяющимися переменными вида f 1 ( y ) · g 1 ( x ) d y = f 2 ( y ) · g 2 ( x ) d x или f 1 ( y ) · g 1 ( x ) · y ‘ = f 2 ( y ) · g 2 ( x )

Решить уравнения с разделенными переменными можно путем интегрирования обеих его частей: ∫ f ( y ) d y = ∫ f ( x ) d x

К числу дифференциальных уравнений с разделенными переменными можно отнести следующие из них:

В ряде случаев прежде, чем производить замену, необходимо произвести преобразования исходного уравнения.

Подробный разбор теории и алгоритмов решения задач мы привели в разделе «Дифференциальные уравнения с разделяющимися переменными».

Линейные неоднородные дифференциальные уравнения первого порядка y ‘ + P ( x ) · y = Q ( x )

Приведем примеры таких уравнений.

Дифференциальное уравнение Бернулли y ‘ + P ( x ) y = Q ( x ) y a

Приведем примеры подобных уравнений.

К числу дифференциальных уравнений Бернулли можно отнести:

Алгоритм применения обоих методов приведен в разделе «Дифференциальное уравнение Бернулли». Там же можно найти подробный разбор решения примеров по теме.

Для более подробного ознакомления с теорией и алгоритмами решения примеров можно обратиться к разделу «Уравнения в полных дифференциалах».

Дифференциальные уравнения второго порядка

Значения корней характеристического уравнения определяет, как будет записано общее решение дифференциального уравнения. Возможные варианты:

исходного уравнения. Получаем: y = y 0 + y

Способ нахождения y 0 мы рассмотрели в предыдущем пункте. Найти частное решение y

Линейные однородные дифференциальные уравнения (ЛОДУ) y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = 0 и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x )

Линейные однородные и неоднородные дифференциальные уравнения и постоянными коэффициентами являются частными случаями дифференциальных уравнений этого вида.

Частные решения мы можем выбрать из систем независимых функций:

Однако существуют примеру уравнений, для которых частные решения не могут быть представлены в таком виде.

Общее решение линейного неоднородного дифференциального уравнения y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x ) мы можем найти в виде суммы y = y 0 + y

частное решение исходного дифференциального уравнения. Найти y 0 можно описанным выше способом. Определить y

нам поможет метод вариации произвольных постоянных.

Более подробно этот раздел освещен на странице «Линейные дифференциальные уравнения второго порядка».

Дифференциальные уравнения высших порядков

Дифференциальные уравнения, допускающие понижение порядка

d 2 y d x 2 = d p d y d y d x = d p d y p ( y ) d 3 y d x 3 = d d p d y p ( y ) d x = d 2 p d y 2 d y d x p ( y ) + d p d y d p d y d y d x = = d 2 p d y 2 p 2 ( y ) + d p d y 2 p ( y )
Полученный результаты подставляем в исходное выражение. При этом мы получим дифференциальное уравнение, порядок которого на единицу меньше, чем у исходного.

Более подробно решения задач по теме рассмотрены в разделе «Дифференциальные уравнения, допускающие понижение порядка».

Решение уравнений данного вида предполагает выполнение следующих простых шагов:

— частное решение неоднородного дифференциального уравнения.

Нахождение корней характеристического уравнения подробно описано в разделе «Решение уравнений высших степеней». Для нахождения y

целесообразно использовать метод вариации произвольных постоянных.

Более детальный разбор теории и примеров по теме вы можете найти на странице « Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами».

Найти решение ЛНДУ высших порядков можно благодаря сумме y = y 0 + y

— частное решение неоднородного дифференциального уравнения.

После того, как мы найдем общее решение ЛОДУ, найти частное решение соответствующего ЛНДУ можно благодаря методу вариации произвольных постоянных. Итак, y = y 0 + y

Получить более подробную информацию по теме можно в разделе «Дифференциальные уравнения высших порядков».

Системы дифференциальных уравнений вида d x d t = a 1 x + b 1 y + c 1 d y d t = a 2 x + b 2 y + c 2

Данная тема подробно разобрана на странице «Системы дифференциальных уравнений». Там же приведены примеры задач с подробных разбором.

Источник

Однородные дифференциальные уравнения

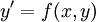
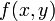
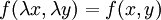
Обыкновенное уравнение первого порядка называется однородным относительно x и y, если функция является однородной степени 0:

.

Однородную функцию можно представить как функцию от :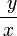

.

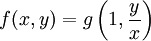
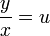
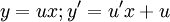
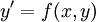
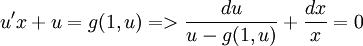
С помощью подстановки (так как ) дифференциальное уравнение сводится к уравнению с разделяющимися переменными:

.

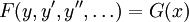
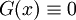
Дифференциальное уравнение является однородным, если оно не содержит свободного члена — слагаемого, не зависящего от неизвестной функции. Так, можно говорить, что уравнение — однородно, если .

В случае, если 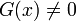, говорят о неоднородном дифференциальном уравнении.

Именно для решения линейных однородных диф. уравнений была построена целая теория, чему способствовало выполнение у них принципа суперпозиции.

См. также

Полезное

Смотреть что такое «Однородные дифференциальные уравнения» в других словарях:

Дифференциальные уравнения с отклоняющимся аргументом — уравнения, связывающие аргумент, а также искомую функцию и её производные, взятые, вообще говоря, при различных значениях этого аргумента (в отличие от обычных дифференциальных уравнений (См. Дифференциальные уравнения)). Примерами могут… … Большая советская энциклопедия

Простейшие дифференциальные уравнения первого порядка — Простейшие дифференциальные уравнения первого порядка класс дифференциальных уравнений первого порядка, наиболее легко поддающихся решению и исследованию. К нему относятся уравнения в полных дифференциалах, уравнения с разделяющимися… … Википедия

Уравнения Эйлера — Лагранжа — Уравнения Эйлера Лагранжа (в физике также уравнения Лагранжа Эйлера или уравнения Лагранжа) являются основными формулами вариационного исчисления, c помощью которых ищутся стационарные точки и экстремумы функционалов. В частности, эти… … Википедия

Максвеллоподобные гравитационные уравнения — В гравитации, Максвеллоподобные гравитационные уравнения составляют систему из четырех уравнений в частных производных, которые описывают свойства электроподобных и магнитоподобных гравитационных полей, а также их источников зарядовой плотностью… … Википедия

ЛАГРАНЖА УРАВНЕНИЯ — механики обыкновенные дифференциальные уравнения 2 го порядка, описывающие движения механич. систем под действием приложенных к ним сил. Л. у. установлены Ж. Лаг ранжем [1] в двух формах: Л. у. 1 го рода, или уравнения в декартовых координатах с… … Математическая энциклопедия

Цепь Маркова — Пример цепи с двумя состояниями Цепь Маркова последовательность случайных событий с конечным или счётным числом исходов, характеризующаяся тем свойством, что, го … Википедия

Длинная линия — Содержание 1 Дифференциальные уравнения длинной линии 1.1 Первичные параметры … Википедия

Маркова цепь — Цепь Маркова последовательность случайных событий с конечным или счётным бесконечным числом исходов, характеризующаяся тем свойством, что, говоря нестрого, при фиксированном настоящем будущее независимо от прошлого. Названа в честь А. А. Маркова … Википедия

Источник