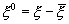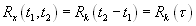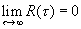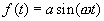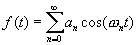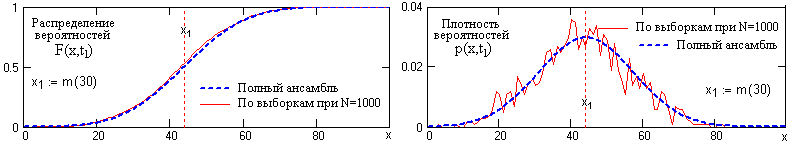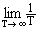что такое одномерная плотность вероятности случайного процесса
Плотность распределения вероятности
Плотность распределения вероятности случайного процесса определяет среднюю вероятность того, что значения процесса в произвольный момент времени будут заключены в определенном интервале.
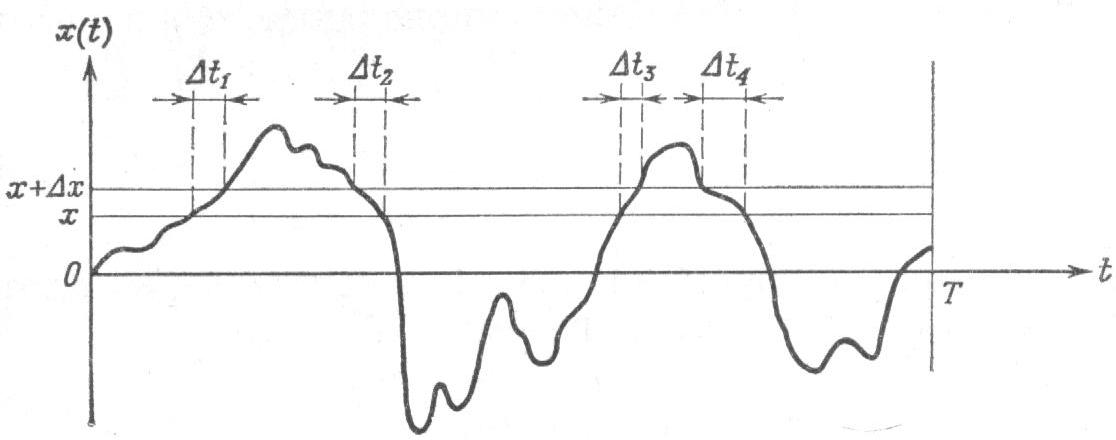
Рассмотрим некоторую реализацию СП как функцию времени (рисунок 1.9).
– реализация СП, 
– время наблюдения
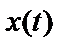
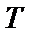
Рисунок 1.9 – Определение плотности распределения вероятности
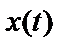
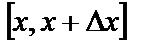
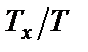
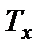
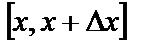
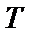
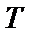
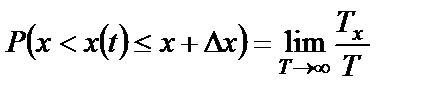
Вероятность того, что значения попадут в интервал 
можно найти, вычисляя отношение 
, где 
– суммарная продолжительность нахождения значений процесса в интервале за время наблюдения . При стремлении к бесконечности это отношение все точнее будет описывать вероятность такого события:
, (1.20)
где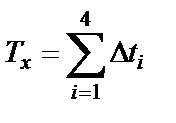 
.
При малых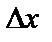 
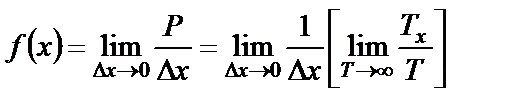
плотность распределения вероятности СП определяется соотношением
. (1.21)
Зная плотность распределения вероятности СП, можно рассчитать его усредненные характеристики, используя, например, следующие соотношения для среднего значения и среднего квадрата:
, 
.
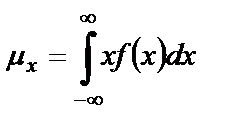
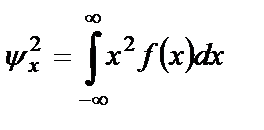
Во многих практических задачах приходится вычислять математическое ожидание некоторой функции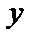 
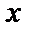
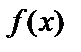
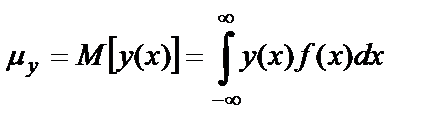
от случайной величины 
, имеющей плотность распределения вероятности 
. Такое вычисление выполняется по следующей формуле:
. (1.22)
При анализе случайных явлений используется большое число различных плотностей вероятности. Рассмотрим две из них, которые хорошо описывают широкий класс практически важных случайных явлений.
Плотности большого числа случайных процессов хорошо аппроксимируются выражением вида
, (1.23)
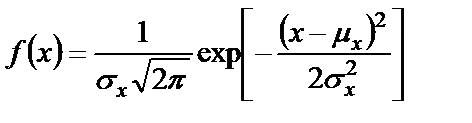
где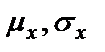 
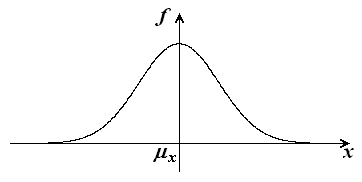
– среднее значение и среднеквадратичное отклонение соответственно.
Функцию (1.23) называют нормальной, или гауссовской, плотностью, она характеризует случайный шум (широкополосный или узкополосный), для которого среднее значение наиболее вероятно. График нормальной плотности имеет колоколообразную форму (рисунок 1.10).
Рисунок 1.10 – Нормальная плотность распределения
Важность нормального распределения определяется широким применением на практике центральной предельной теоремы, которая формулируется следующим образом: сумма большого числа совместно действующих независимых случайных величин распределена в общем случае по закону, близкому к нормальному.
По двум причинам желательно иметь возможность предполагать, что случайный процесс имеет нормальную плотность распределения:
1) нормальное распределение полностью определяется только двумя параметрами – средним значением и среднеквадратичным отклонением;
2) все линейные операции такие, как интегрирование, дифференцирование, преобразование Фурье, выполняемые над нормально распределенными случайными величины, дают в результате также нормально распределенные величины.
Наиболее распространенный вид детерминированных процессов – это периодические процессы, разлагаемые на гармонические составляющие. Для описания одной такой составляющей не требуется вероятностных понятий, поскольку ее точное значение в любой момент времени вычисляется по формуле
.
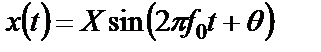
Однако гармоническое колебание можно рассматривать также как выборочную функцию случайного процесса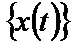 
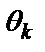
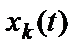
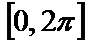
, где начальная фаза 
каждой выборочной функции 
является случайной величиной, равномерно распределенной в интервале 
.
Плотность распределения вероятности такого случайного гармонического процесса определяется формулой
(1.24)
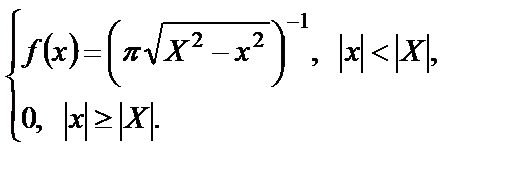
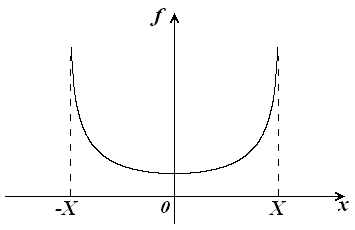
График функции (1.24) имеет чашеобразную форму (рисунок 1.11), откуда видно, что плотность гармонического процесса достигает минимума в точке с координатой, равной среднему значению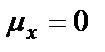 
.
Рисунок 1.11 – Плотность распределения гармонического процесса
1. Характеристики и свойства случайного процесса
Случайный процесс описывается статистическими характеристиками, называемыми моментами. Кроме того, важнейшими характеристиками случайного процесса являются его стационарность и эргодичность, а также спектр мощности.
Одномерная плотность распределения вероятности W(x,t) определяет вероятность
того, что случайная величина x (t) лежит в интервале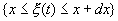 
с помощью функции W(x,t) можно провести усреднение как случайной величины x (t), так и любой функции от нее.
Средним значением случайного процесса или его первым моментом называется интеграл
Второй начальный момент случайного процесса описывается интегралом
и определяет среднюю мощность случайного процесса.
При анализе случайных процессов часто интерес представляет флуктуационная составляющая. Введем понятие центрированного случайного процесса 
Второй центральный момент определяет мощность флуктуационной составляющей случайного процесса и называется дисперсией
Аналогично можно определить также моменты случайного процесса более высокого порядка.
Таким образом, используя одномерную плотность распределения вероятности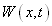 
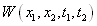
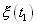
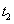
можно получить параметры случайного процесса, которые являются усреднением по множеству (ансамблю) реализаций данного случайного процесса в каком либо его «сечении», то есть в фиксированный момент времени t. Но задание одномерной плотности распределения вероятности не дает возможность определить характер изменения случайного процесса во времени и не характеризует взаимосвязь случайного процесса в различные моменты времени. Для этого вводят понятие двумерной плотности распределения вероятности 
, описывающей связь двух значений 
и 
в произвольные моменты времени 
1 и 
.
С помощью двумерной плотности распределения вероятности можно определить автокорреляционную (ковариационную) функцию
а также автокорреляционную функцию центрированного случайного процесса
Случайный процесс называется стационарным, если одномерная плотность распределения вероятности и, следовательно, среднее значение и дисперсия случайного процесса не зависят от времени, а двумерная плотность распределения вероятности и автокорреляционная функция зависят только от разности временных аргументов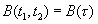 
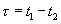
, где 
.
Если многомерный закон распределения вероятностей распределения мгновенных значений, взятых в разные моменты времени, не зависят от принятого начала отсчёта, а зависят только от интервалов между выбранными моментами
то такой процесс стационарен в узком смысле. Если независимость от начала отсчёта выполняется только до второго (корреляционного) момента (включая первый), то такой процесс называют стационарным в широком смысле.
Случайный процесс называется эргодическим первого порядка, если его первый момент, полученный усреднением по множеству реализаций (1.2), с вероятностью сколь угодно близкой к единице совпадает со средним значением, полученным усреднением по времени одной достаточно длинной реализации.
Случайный процесс называется эргодическим второго порядка, если его корреляционная функция (1.6), с вероятностью сколь угодно близкой к единице совпадает со средним значением произведения случайного процесса при сдвинутых аргументах, полученным усреднением по времени одной достаточно длинной реализации.
Параметры эргодического случайного процесса могут быть определены так:
Усреднением по времени могут быть найдены также автокорреляционные функции эргодического случайного процесса
В данной работе предполагается, что аддитивно добавленный к полезному сигналу «шум» является эргодическим, случайным процессом.
Корреляционные функции — важнейшие характеристики случайных процессов.
Приведем их основные свойства:
1. 
(1.11)
2. 
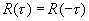
(1.12)
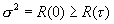
3. 
Формально можно вычислить автокорреляционную функцию (1.10) и для детерминированного процесса, например, для периодической функции
автокорреляционная функция описывается следующим выражением
Для периодической функции, представимой рядом Фурье
Таким образом, автокорреляционная функция периодической функции текущего времени t является также периодической функцией от аргумента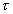 
— величины временного сдвига.
Случайные процессы и функции
Нет ничего более противного разуму и постоянству природы, чем случайность.
Сам бог не может знать того, что произойдет случайно.
Ибо если знает, то это определенно произойдет,
а если определенно произойдет, то не случайно.
Марк Туллий Цицерон. О девинации.
Римский философ и политик, I в.д.н.э.
Случайный процесс Х(t) представляет собой функцию, которая отличается тем, что принимаемые ею значения в любые произвольные моменты времени по координате t являются случайными. Строго с теоретических позиций, случайный процесс X(t) следует рассматривать как совокупность временных функций x k (t), имеющих определенную общую статистическую закономерность. При регистрации случайного процесса на определенном временном интервале осуществляется фиксирование единичной реализации x k (t) из бесчисленного числа возможных реализаций процесса X(t). Эта единичная реализация называется выборочной функцией случайного процесса X(t). Примеры выборочных функций модельного случайного процесса X(t) приведены на рис. 17.1.1. В дальнейшем без дополнительных пояснений при рассмотрении различных параметров и характеристик случайных процессов для сопровождающих примеров будем использовать данную модель процесса.
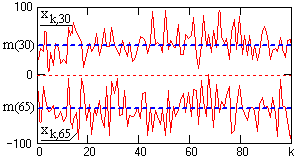
Рис. 17.1.1. Выборочные функции случайного процесса.
Функциональные характеристики случайного процесса.
Допустим, что случайный процесс X(t) задан ансамблем реализаций
Одномерная функция распределения вероятностей (x,t i ) определяет вероятность того, что в момент времени t i значение случайной величины X(t i ) не превысит значения x:
Моменты времени t i являются сечениями случайного процесса X(t) по пространству возможных состояний и плотность вероятностей p(x,t i ) представляет собой плотность вероятностей случайных величин X(t i ) данных сечений. Произведение p(x,t i )·dx равно вероятности реализации случайной величины X(t i ) в бесконечно малом интервале dx в окрестности значения x, откуда следует, что плотность вероятностей также является неотрицательной величиной.
Рис. 17.1.3. Распределение вероятностей и плотность вероятностей сечения случайного процесса
При известной функции плотности вероятностей вероятность реализации значения X(t i ) в произвольном интервале значений [a, b] вычисляется по формуле:
P(a i )≤b) =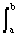
p(x,t i ) dx.
Функция плотности вероятностей должна быть нормирована к 1, т.к. случайная величина обязана принимать какое-либо значение из числа возможных, образующих полное пространство случайных величин:
p(x,t i ) dx =1.
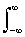
По известной плотности распределения вычисляется и функция распределения вероятностей:
F(x,t i ) =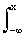
p(x,t i ) dx.
Случайные процессы и их функции характеризуются неслучайными функциями математического ожидания (среднего значения), дисперсии и корреляции:
Математическое ожидание (mean v alue) представляет собой статистическое усреднение случайной величины X(t i ), под которым понимают усреднение по ансамблю реализаций в каком либо фиксированном сечении t i случайного процесса. Соответственно, функция математического ожидания является теоретической оценкой среднего взвешенного значения случайного процесса по временной оси:
m x (t) є M <Х(t)>є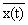 
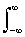
=x p(x;t) dx, (17.1.1)
Функция дисперсии (variance) случайного процесса является теоретической оценкой среднего взвешенного значения разности Х(t)-m x (t), которая называется флюктуационной частью процесса:
D x (t) = M <[Х(t)-m x (t)] 2 >= M 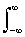[x o (t)] 2 p(x;t) dx, (17.1.2)
Функция среднего квадратического отклонения (standard deviation) служит амплитудной мерой разброса значений случайного процесса по временной оси относительно математического ожидания процесса:
s x (t) =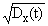
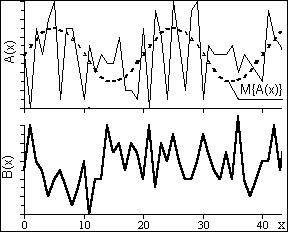
. (17.1.3)
На рис. 17.1.4 приведен пример флюктуационной составляющей процесса X(t) (рис. 17.1.1) в одной из реализаций в сопоставлении со средним квадратическим отклонением ± s случайных величин от математического ожидания m(t).
Корреляционные функции случайных процессов. Одномерные законы плотности распределения вероятностей случайных процессов не несут каких-либо характеристик связи между значениями случайных величин для различных значений аргументов.
Характеристикой динамики изменения двумерной случайной величины
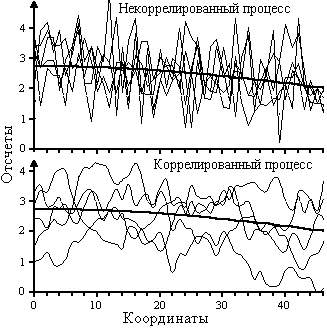
На рис. 17.1.5 приведены примеры реализаций двух случайных процессов, которые характеризуются одной и той же функцией математического ожидания и дисперсии.
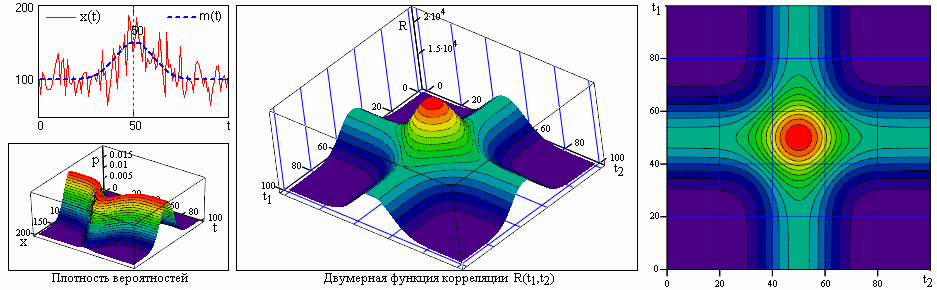
Рис. 17.1.6. Двумерная плотность вероятностей и корреляционная функция процесса X(t).
На рис. 17.1.6 приведена форма модельного случайного процесса X(t) в одной выборке со значительной и изменяющейся неслучайной составляющей. Модель задана на интервале 0-Т (Т=100) в дискретной форме с шагом D t=1. Корреляционная функция вычислена по заданной плотности вероятностей модели
При анализе случайных процессов второй момент времени t j удобно задавать величиной сдвига t относительно первого момента, который при этом может быть задан в виде координатной переменной:
Функция, задаваемая этим выражением, обычно называется автокорреляционной функцией случайного процесса.
Ковариационные функции. Частным случаем корреляционной функции является функция автоковариации (ФАК), которая широко используется при анализе сигналов. Она представляет собой статистически усредненное произведение значений центрированной случайной функции X(t)-m x (t) в моменты времени t i и t j и характеризует флюктуационную составляющую процесса:
В терминах теории вероятностей ковариационная функция является вторым центральным моментом случайного процесса. Для центрированных случайных процессов ФАК тождественна функции корреляции. При произвольных значениях m x ковариационные и корреляционные функции связаны соотношением:
Нормированная функция автоковариации (функция корреляционных коэффициентов):
r Х (t,t+ t ) = K Х (t,t+ t ) / [ s (t) s (t+ t )]. (17.1.6)
При t = 0 значение r Х равно 1, а ФАК вырождается в дисперсию случайного процесса:
Отсюда следует, что для случайных процессов и функций основными характеристиками являются функции математического ожидания и корреляции (ковариации). Особой необходимости в отдельной функции дисперсии не имеется.
Рис. 17.1.7. Реализации и ковариационные функции случайных процессов.
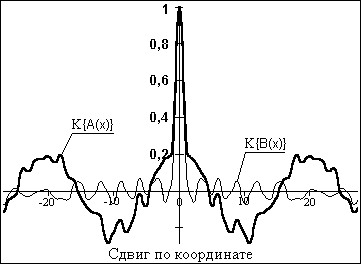
Примеры реализаций двух различных случайных процессов и их нормированных ковариационных функций приведены на рис. 17.1.7.
Свойства функций автоковариации и автокорреляции.
1. Максимум функций наблюдается при t = 0. Это очевидно, т.к. при t = 0 вычисляется степень связи отсчетов с собой же, которая не может быть меньше связи разных отсчетов. Значение максимума функции корреляции равно средней мощности сигнала.
Заметим, что для некоррелированных процессов при t Ю Ґ значение T k стремится к 2, что несколько противоречит физическому смыслу радиуса корреляции, который в этом случае должен был бы стремиться к 1. С учетом последнего эффективный интервал корреляции целесообразно определять по формуле:
4. Если к случайной функции X(t) прибавить неслучайную функцию f(t), то ковариационная функция не изменяется.
6. При умножении функции случайного процесса на постоянное значение С значения ФАК увеличиваются в С 2 раз.
Взаимные моменты случайных процессов второго порядка дают возможность оценить совместные свойства двух случайных процессов X(t) и Y(t) путем анализа произвольной пары выборочных функций x k (t) и y k (t).
Взаимные функции являются произвольными функциями (не обладают свойствами четности или нечетности), и удовлетворяют следующим соотношениям:
R xy (- t ) = R yx ( t ), (17.1.10)
|R xy ( t )| 2 Ј R x (0)R y (0).
Если один из процессов центрированный, то имеет место R xy (t) = K xy (t).
Нормированная взаимная ковариационная функция (коэффициент корреляции двух процессов), которая характеризует степень линейной зависимости между случайными процессами при данном сдвиге t одного процесса по отношению ко второму, определяется выражением:
r xy ( t ) = K xy ( t )/( s x s y ). (17.1.11)
Статистическая независимость случайных процессов определяет отсутствие связи между значениями двух случайных величин X и Y. Это означает, что плотность вероятности одной случайной величины не зависит от того, какие значения принимает вторая случайная величина. Двумерная плотность вероятностей при этом должна представлять собой произведения одномерных плотностей вероятностей этих двух величин:
Это условие является обязательным условием статистической независимости случайных величин. В противном случае между случайными величинами может существовать определенная статистическая связь. Как линейная, так и нелинейная. Мерой линейной статистической связи является коэффициент корреляции:
r xy = [ M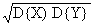 
.
Классификация случайных процессов. Случайные процессы различают по степени однородности их протекания во времени (по аргументу).
Нестационарные процессы. В общем случае значения функций математического ожидания, дисперсии и корреляции могут быть зависимыми от момента времени t, т.е. изменяться во времени. Такие процессы составляют класс нестационарных процессов.
m Х (t 1 ) = m Х (t 2 ) = m Х = const, (17.1.12)
D Х (t 1 ) = D Х (t 2 ) = D Х = const,
Последние выражения свидетельствует о четности корреляционной (а равно и ковариационной) функции и функции корреляционных коэффициентов. Из него вытекает также еще одно свойство смешанных моментов стационарных процессов:
Чем медленнее по мере увеличения значений t убывают функции R x ( t ) и r x ( t ), тем больше эффективный интервал корреляции случайного процесса, и тем медленнее изменяются во времени его реализации.
Стационарные случайные процессы наиболее часто встречаются при решении физических и технических задач. Теория стационарных случайных функций разработана наиболее полно и для ее использования обычно достаточно определения стационарности в широком смысле : случайная функция считается стационарной, если ее математическое ожидание постоянно, а корреляционная функция зависит только от одного аргумента. Случайные процессы, удовлетворяющие условиям стационарности на ограниченных, интересующих нас интервалах, также обычно относят к числу стационарных в широком смысле и называют квазистационарными.
Эргодические процессы. Строго корректно характеристики случайных процессов оцениваются путем усреднения по ансамблю реализаций в определенные моменты времени (по сечениям процессов). Но большинство стационарных случайных процессов обладает эргодическим свойством. Сущность его заключается в том, что по одной достаточно длинной реализации процесса можно судить о всех его статистических свойствах так же, как по любому количеству реализаций. Другими словами, закон распределения случайных величин в таком процессе может быть одним и тем же как по сечению для ансамбля реализаций, так и по координате развития. Такие процессы получили название эргодических (ergodic). Для эргодических процессов имеет место:
m X (t) = M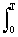 
x(t) dt, (17.1.13)
R Х ( t ) = M 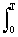x(t)x(t+ t ) dt. (17.1.15)
Эргодичность является очень важным свойством случайных стационарных, и только стационарных процессов. Математическое ожидание эргодического случайного процесса равно постоянной составляющей любой его реализации, а дисперсия является мощностью его флюктуационной составляющей. Так как определение функций производится по ограниченным статистическим данным одной реализации и является только определенным приближением к соответствующим фактическим функциям процессов, целесообразно называть эти функции статистическими. Заметим, что, как это следует из (17.1.15), вычисление корреляционной функции подобно свертке (с делением на интервал реализации) и может записываться символически:
R Х ( t ) = (1/T) x(t) * x(t+ t ).
Свойства эргодичности могут проявляться только по отношению к двум первым моментам случайного процесса, что вполне достаточно для использования соответствующих методик исследования процессов. Практическая проверка эргодичности процесса обычно производится проверкой выполнения условия Слуцкого:
K( t ) d t = 0. (17.1.16)
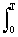
Если ковариационная функция процесса стремится к нулю при возрастании значения аргумента ( t ), то процесс относится к числу эргодических, по крайней мере относительно моментов первого и второго порядков.
Релятивисты и позитивисты утверждают, что «мысленный эксперимент» весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.
Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.