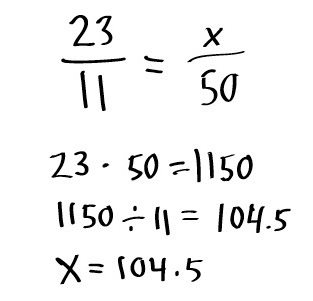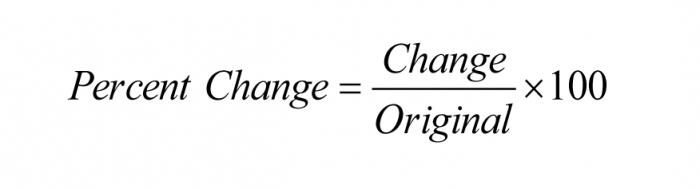что такое обратный процент

Что такое процент? Формула процентов. Проценты

Что означает процент

В переводе с латыни процент (per centum) означает «на сотню» или «сотая», то есть одна сотая доля числа. Принято обозначение знаком «%». Процент принято использовать, когда хотят указать точную долю чего-либо к одной единице. 100% – 1, соответственно, 25% – это 0,25 и 25/100.

Также с помощью этого понятия можно сравнивать разные величины, предварительно указывая, из какого целого нужно вычесть проценты. Скажем, доход больше расхода на 25%, стоимость авиабилетов снизилась на 3%, если сравнить с прошлогодними расценками, книга «Орден феникса» на 35% толще, чем «Кубок огня» и так далее. Бывает ситуация, когда процент получается больше 100, это значит, что доля вышла больше 1.

В финансах процент является оплатой заемщика кредитору за деньги, полученные на время. Процентщик – это человек, выдающий деньги на время под определённый процент. Человек, который брал кредит, в дальнейшем будет вынужден вернуть изначально взятую сумму, да ещё и доплатить сверху.

В бизнесе существует определение «работа за проценты», в таком случае размер заработной платы напрямую зависит от прибыли или оборота. Этот принцип несёт в себе как позитивные возможности, так и определенный риск, ведь с одной стороны можно заработать много, а можно не заработать ничего. Без процентов невозможно представить функционирования не только бизнеса, но и банков с бухгалтерией.

Процент элементарно понять благодаря самому знаку «%» – в символе скрыт весь смысл. Наклонная черта / означает деление, а два небольших ноля на 100. Вот и выходит, что 20% – это 20 делить на 100, получается 0,2.

Видео

Перевод процента в десятичную дробь

Пожалуй, нет ничего проще, чем видоизменить процент в десятичную дробь.Для расчета вам понадобятся проценты, которые разделить на 100.

Если перед вами стоит цель получить десятичную дробь из 75 %, то элементарнее задачи просто не придумаешь.

Увеличение, уменьшение числа на заданное количество процентов

Школьники должны усвоить, что такое проценты, как считать их и решать разнообразные задачи. Для этого нужно понимать, как увеличивается или уменьшается число на N%.

Зачастую даются задания, да и в жизни нужно узнать, чему будет равно число, увеличенное на заданное количество процентов. К примеру, дано число Х. Нужно узнать, чему будет равно значение Х, если его увеличить, допустим, на 40%. Сначала нужно перевести 40% в дробное число (40/100). Итак, результатом увеличения числа Х станет: Х + 40% ∙ Х= ( 1+40 /₁₀₀) ∙ Х = 1,4 ∙ Х. Если вместо Х подставить любое число, возьмем, к примеру, 100, тогда все выражение будет равно: 1,4 ∙ Х = 1,4 ∙ 100 = 140.

Встречаются задания, где нужно узнать, на сколько процентов увеличилось число.

К примеру, дана задача: Машинист ехал по одному участку пути со скоростью 80 км/ч. На другом участке скорость поезда возросла до 100 км/ч. На сколько процентов возросла скорость поезда?

Предположим, 80 км/ч – 100%. Тогда производим расчеты: (100% ∙ 100 км/ч) / 80 км/ч= 1000 : 8 = 125%. Получается, что 100 км/ч – это 125%. Чтобы узнать, на сколько увеличилась скорость, нужно вычислить: 125% — 100% = 25%.

Ответ: на 25% увеличилась скорость поезда на втором участке.

Изменение числа на сколько-то процентов

Когда говорят, что число увеличилось на \( \displaystyle x\), это значит, что к числу надо прибавить \( \displaystyle x\).

Если же число уменьшилось на \( \displaystyle x\), это значит, что из числа надо вычесть \( \displaystyle x\).

Рассмотрим пример:

Цена холодильника в магазине за год увеличилась на \( \displaystyle 5\%\). Какой стала цена, если изначально холодильник стоил \( \displaystyle 12500\)р?

Решение:

Для начала определим, на сколько рублей изменилась (в данном случае – увеличилась) стоимость холодильника. По условию – на \( \displaystyle 5\%\). Но \( \displaystyle 5\%\) от чего? Конечно же, от самой начальной стоимости холодильника (\( \displaystyle 12500\) р). Получается, что нам нужно найти \( \displaystyle 5\%\) от \( \displaystyle 12500\)р:

\( \displaystyle 0,05\cdot 12500=625\).

Теперь мы знаем, что цена увеличилась на \( \displaystyle 625\)р. Остается только, согласно правилу, прибавить к начальной стоимости величину изменения:

Новая цена \( \displaystyle=12500+625=13125\) рублей.

Ответ: \( \displaystyle 13125.\)

Еще пример (постарайся решить самостоятельно):

Книга «Математика для чайников» в магазине стоит \( \displaystyle 360\)р. Во время акции все книги продаются со скидкой \( \displaystyle 15\%.\). Сколько теперь придется заплатить за эту книгу?

Решение:

Что такое скидка, ты наверняка знаешь? Скидка в \( \displaystyle 15\%.\) означает, что стоимость товара уменьшили на \( \displaystyle 15\%.\).

На сколько уменьшилась стоимость книги (в рублях)? Нужно найти \( \displaystyle 15\%.\) от начальной ее стоимости в \( \displaystyle 360\)р:

\( \displaystyle 0,15\cdot 360=54\).

Цена уменьшилась, значит нужно из начальной стоимости вычесть то, на сколько она уменьшилась:

Новая цена \( \displaystyle=360-54=306\) рублей.

Ответ: \( \displaystyle 306\).

Правда ведь просто?

Но есть способ сделать это решение еще проще и короче!

Рассмотрим пример:

Увеличьте число \( \displaystyle x\) на \( \displaystyle 23\%\).

Чему равны \( \displaystyle 23\%\) от \( \displaystyle x\)? Как мы уже выяснили раньше, это будет \( \displaystyle 0,23x\).

Теперь увеличим само число x на эту величину:

Получается, что в результате мы к десятичной записи \( \displaystyle 23\%\) прибавили \( \displaystyle 1\) и умножили на число \( \displaystyle x\). Обобщим это правило:

Пусть нам нужно увеличить число \( \displaystyle x\) на \( \displaystyle p\%\).

\( \displaystyle p\%\) от числа \( \displaystyle x\) – это \( \displaystyle \frac

<100>\cdot x\).

Тогда новое число будет равно: \( \displaystyle x+\frac

<100>\cdot x=x\left( 1+\frac

<100>\right)\).

Чтобы увеличить число на \( \displaystyle p\%\), нужно умножить его на \( \displaystyle \left( 1+\frac

<100>\right)\).

Например, увеличим число \( \displaystyle 136\) на \( \displaystyle 28\%\):

\( \displaystyle 136\cdot \left( 1+0,28 \right)=136\cdot 1,28=\text<174>\text<,08>\).

Примеры задач на проценты

1. Сколько процентов от числа 36 составляет число 9?

По формуле нахождения процента от числа, нужно 9 умножить на 100 и поделить на 36.

Ответ: число 9 составляет 25% от 36.

2. Вычислить число С, которое составляет 10% от 40.

По формуле нахождения числа по его проценту, нужно 40 умножить на 10 и результат разделить на 100.

Ответ: число 4 составляет 10% от 40.

3. Первый партнер вложил в бизнес 4500 рублей, второй – 3500 рублей, третий – 2000 рублей. Они получили прибыль 2400 рублей. Прибыль они разделили поровну. Сколько в рублях потерял первый партнер, по сравнению с тем, сколько бы он получил, если бы они разделили доход согласно проценту вложенных средств?

Итак, вместе они вложили 10 000 рублей. Доход на каждого составил равную долю по 800 рублей. Чтобы узнать, сколько должен был получить первый партнер и сколько он, соответственно, потерял, нужно узнать процент вложенных средств. Затем нужно узнать, сколько в рублях прибыли составляет этот вклад. И последнее — вычесть 800 рублей из полученного результата.

Ответ: первый партнер потерял 280 рублей при разделе прибыли.

Процентный пункт

Как найти процент?

Принцип нахождения процента такой же, как и обычное нахождение дроби от числа. Чтобы найти процент от чего-либо, нужно это чего-либо разделить на 100 частей и полученное число умножить на нужный процент.

Например, найти 2% от 10 см.

Найти от 10 см

А как решать подобные задания мы уже знаем. Это обычное нахождение дроби от числа. Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.

Итак, делим число 10 на знаменатель дроби

Получили 0,1. Теперь 0,1 умножаем на числитель дроби

Получили ответ 0,2. Значит 2% от 10 см составляет 0,2 см. А если перевести 0,2 сантиметра в миллиметры, то получим 2 миллиметра:

Значит 2% от 10 см составляют 2 мм.

Пример 2. Найти 50% от 300 рублей.

Чтобы найти 50% от 300 рублей, нужно эти 300 рублей разделить на 100, и полученный результат умножить на 50.

Итак, делим 300 рублей на 100

Теперь полученный результат умножаем на 50

Значит 50% от 300 рублей составляет 150 рублей.

Если на первых порах сложно привыкнуть к записи со значком %, можно заменять эту запись на обычную дробную запись.

Например, те же 50% можно заменить на запись . Тогда задание будет выглядеть так: Найти от 300 рублей, а решать такие задачи для нас пока проще

В принципе, ничего сложного здесь нет. Если возникают сложности, советуем остановиться и заново изучить дроби и как их можно применять.

Пример 3. Швейная фабрика выпустила 1200 костюмов. Из них 32% составляют костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?

Здесь нужно найти 32% от 1200. Найденное число будет ответом к задаче. Воспользуемся правилом нахождения процента. Разделим 1200 на 100 и полученный результат умножим на искомый процент, т.е. на 32

Ответ: 384 костюмов нового фасона выпустила фабрика.

Основная связь между десятичными дробями и процентами

Если нужно перевести десятичную дробь в проценты, то ее умножают на 100 и дописывают знак %.

Если нужно совершить обратную операцию — перевести проценты в десятичную дробь, то число делят на 100%.

Переведите 56% в десятичную дробь. Объяснение. Чтобы перевести проценты в десятичную дробь, нужно число процентов разделить на 100%. При делении на 100 по правилу отсчитываем в числе количество знаков справа налево, равное количеству нулей, и ставим запятую. Значит, при делении на сто запятую ставим, отсчитав два знака влево от конца записи числа. Получим 0,56. 56%=56%:100%=56:100=,56. Ответ: 0,56.

Задачи на проценты подробнее

Что такое процент? Откуда взялось это слово?

Все очень просто. Слово процент произошло от латинского per cent– на сотню, и означает оно «сотая доля» или «сотая часть».

То есть один процент любого числа – это одна сотая этого числа.

И все. Этого достаточно, чтобы решать задачи, в которых присутствует это противное слово «процент».

Например: чему равны \( \displaystyle 34\%\) от числа \( \displaystyle 120\)?

Прочтем это задание по-другому: чему равны \( \displaystyle 34\) сотых доли числа \( \displaystyle 120\)?

Элементарно, правда? Нужно разделить число \( \displaystyle 120\) на \( \displaystyle 100\) частей (чтобы узнать, чему равна одна сотая доля – один процент) и взять \( \displaystyle 34\) таких части:

\( \displaystyle \frac<120><100>\cdot 34=1,2\cdot 34=40,8\).

Сколько процентов содержится в числе?

Снова перефразируем вопрос, заменив слово «процент» на «сотую часть»: Сколько сотых частей находится в числе?

Ответ сразу становится очевидным: в любом числе или предмете находится ровно сто сотых частей (то есть, если разделить число или предмет на \( \displaystyle 100\) частей, сколько будет этих частей?

Очевидно же, что \( \displaystyle 100\)).

Разберем еще несколько примеров

Метод решения задач с процентами

Все соотношения и формулы, полученные для решения задач с процентами, выводятся из пропорции

Данные задачи на проценты можно записать в виде следующих соотношений:

все — 100%часть — часть в %

которые можно записать в виде пропорции

Используя эту пропорцию можно получить формулы для решения основных типов задач на проценты.

Способы нахождения процента

Правило нахождения процентов от числа: Чтобы найти процент от числа, нужно перевести процент в десятичную дробь и умножить на заданное число.

Правило нахождения числа по его проценту: Чтобы найти число по его процентам, нужно:проценты числа перевести в десятичную дробь;заданное число разделить на полученную дробь.

Процентное отношение двух чисел

Чтобы узнать, сколько процентов первое число составляет от второго, надо первое число разделить на второе и результат умножить на 100.

Задача. Завод по годовому плану должен выпустить продукции на сумму 1 250 000 руб. За 1-ый квартал он выпустил её на сумму 450 000 руб. На сколько процентов выполнен заводом годовой план за 1-ый квартал?

Ответ: За 1-ый квартал план выполнен на 36%.

Нахождения числа по его проценту

Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.

Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:

Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2

Мы нашли один процент от общей прибыли, т.е. . Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100

30 000 × 100 = 3 000 000

Мы нашли общую прибыль. Она составляет три миллиона.

Попробуем сформировать правило нахождения числа по его проценту.

Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.

Пример 2. Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.

Читаем первую часть правила:

Чтобы найти число по его проценту, нужно известное число разделить на данный процент

У нас известное число это 35, а данный процент это 7. Разделим 35 на 7

Читаем вторую часть правила:

и полученный результат умножить на 100

У нас полученный результат это число 5. Умножим 5 на 100

500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35

Получили 35. Значит задача была решена правильно.

Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.

Например, предыдущая задача может быть изложена так: число 35 это от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби. Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби. В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100

В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.

Источник

Как посчитать процент обратным счетом

Один процент — это одна сотая доля, обозначается знаком %. Само слово процент происходит от латинского «pro centum», что означает «сотая доля». Проценты — это удобная относительная мера, позволяющая оперировать с числами в привычном для человека формате не зависимо от размера самих чисел. Это своего рода масштаб, к которому можно привести любое число.

Проценты незаменимы в страховании, финансовой сфере, в экономических расчетах. В процентах выражаются ставки налогов, доходность капиталовложений, плата за заемные денежные средства (например, кредиты банка), темпы роста экономики и многое другое.

1. Формула расчета доли в процентном отношении.

Пусть задано два числа: A₁ и A₂. Надо определить, какую долю в процентном отношении составляет число A₁ от A₂.

В финансовых расчетах часто пишут

Пример. Какую долю в процентном отношении составляет 10 от 200

P = 10 / 200 * 100 = 5 (процентов).

2. Формула расчета процента от числа.

Пусть задано число A₂. Надо вычислить число A₁, составляющее заданный процент P от A₂.

Пример. Банковский кредит 10 000 рублей под 5 процентов. Сумма процентов составит.

P = 10000 * 5 / 100 = 500.

3. Формула увеличения числа на заданный процент. Сумма с НДС.

Пусть задано число A₁. Надо вычислить число A₂, которое больше числа A₁ на заданный процент P. Используя формулу расчета процента от числа, получаем:

Пример 1. Банковский кредит 10 000 рублей под 5 процентов. Общая сумма долга составит.

A₂= 10000 * (1 + 5 / 100) = 10000 * 1.05 = 10500.

Пример 2. Сумма без НДС равна 1000 рублей, НДС 18 процентов. Сумма с НДС составляет:

A₂= 1000 * (1 + 18 / 100) = 1000 * 1.18 = 1180.

4. Формула уменьшения числа на заданный процент.

Пусть задано число A₁. Надо вычислить число A₂, которое меньше числа A₁ на заданный процент P. Используя формулу расчета процента от числа, получаем:

Пример. Денежная сумма к выдаче за минусом подоходного налога (13 процентов). Пусть оклад составляет 10 000 рублей. Тогда сумма к выдаче составляет:

A₂= 10000 * (1 — 13 / 100) = 10000 * 0.87 = 8700.

5. Формула вычисления исходной суммы. Сумма без НДС.

Пусть задано число A₁, равное некоторому исходному числу A₂ с прибавленным процентом P. Надо вычислить число A₂. Иными словами: знаем денежную сумму с НДС, надо вычислить сумму без НДС.

Обозначим p = P / 100, тогда:

Пример. Сумма с НДС равна 1180 рублей, НДС 18 процентов. Стоимость без НДС составляет:

A₂= 1180 / (1 + 0.18) = 1000.

6. Расчет процентов на банковский депозит. Формула расчета простых процентов.

Если проценты на депозит начисляются один раз в конце срока депозита, то сумма процентов вычисляется по формуле простых процентов.

S = K + (K*P*d/D)/100
Sp = (K*P*d/D)/100

Где:
S — сумма банковского депозита с процентами,
Sp — сумма процентов (доход),
K — первоначальная сумма (капитал),
P — годовая процентная ставка,
d — количество дней начисления процентов по привлеченному вкладу,
D — количество дней в календарном году (365 или 366).

Пример 1. Банком принят депозит в сумме 100 тыс. рублей сроком на 1 год по ставке 20 процентов.

S = 100000 + 100000*20*365/365/100 = 120000
Sp = 100000 * 20*365/365/100 = 20000

Пример 2. Банком принят депозит в сумме 100 тыс. рублей сроком на 30 дней по ставке 20 процентов.

S = 100000 + 100000*20*30/365/100 = 101643.84
Sp = 100000 * 20*30/365/100 = 1643.84

7. Расчет процентов на банковский депозит при начислении процента на процент. Формула расчета сложных процентов.

Если проценты на депозит начисляются несколько раз через равные промежутки времени и зачисляются во вклад, то сумма вклада с процентами вычисляется по формуле сложных процентов.

S = K * ( 1 + P*d/D/100 ) N

Где:
S — сумма депозита с процентами,
К — сумма депозита (капитал),
P — годовая процентная ставка,
N — число периодов начисления процентов.

При расчете сложных процентов проще вычислить общую сумму с процентами, а потом вычислить сумму процентов (доход):

Sp = S — K = K * ( 1 + P*d/D/100 ) N — K

Sp = K * (( 1 + P*d/D/100 ) N — 1)

Пример 1. Принят депозит в сумме 100 тыс. рублей сроком на 90 дней по ставке 20 процентов годовых с начислением процентов каждые 30 дней.

S = 100000 * (1 + 20*30/365/100) 3 = 105 013.02
Sp = 100000 * ((1 + 20*30/365/100) N — 1) = 5 013.02

Пример 2. Проверим формулу начисления сложных процентов для случая из предыдущего примера.

Разобьем срок депозита на 3 периода и рассчитаем начисление процентов для каждого периода, использую формулу простых процентов.

S₁ = 100000 + 100000*20*30/365/100 = 101643.84
Sp₁ = 100000 * 20*30/365/100 = 1643.84

S₂ = 101643.84 + 101643.84*20*30/365/100 = 103314.70
Sp₂ = 101643.84 * 20*30/365/100 = 1670.86

S₃ = 103314.70 + 103314.70*20*30/365/100 = 105013.02
Sp₃ = 103314.70 * 20*30/365/100 = 1698.32

Общая сумма процентов с учетом начисления процентов на проценты (сложные проценты)

Таким образом, формула вычисления сложных процентов верна.

8. Еще одна формула сложных процентов.

Если процентная ставка дана не в годовом исчислении, а непосредственно для периода начисления, то формула сложных процентов выглядит так.

Где:
S — сумма депозита с процентами,
К — сумма депозита (капитал),
P — процентная ставка,
N — число периодов начисления процентов.

Пример. Принят депозит в сумме 100 тыс. рублей сроком на 3 месяца с ежемесячным начислением процентов по ставке 1.5 процента в месяц.

S = 100000 * (1 + 1.5/100) 3 = 104 567.84
Sp = 100000 * ((1 + 1.5/100) 3 — 1) = 4 567.84

Избавьтесь от утомительных
расчетов с помощью этих Excel-таблиц >>>

Платежный календарь. График и прогноз платежей и поступлений

Расчет себестоимости и рентабельности продукции (услуг)

Расчет инвестиционных проектов

Финансовый анализ МСФО

Финансовый анализ РСБУ (Россия)

Точка безубыточности. Рентабельность продаж

Оценка стоимости бизнеса

Посмотрите полный список таблиц >>>

Разработка Excel-таблиц
экономической и управленческой
тематики. Условия тут >>>

Онлайн калькулятор находит число из которого был вычтен заданный процент.
Зачастую используется для решения задач финансового и бухгалтерского характера, для нахождения суммы до вычета НДС или НДФЛ.

Суть расчетов, в которых используется процент от суммы, заключается в том, что этот процент заложен в 100% изначального числа, которое состоит из суммы различных его частей.

По заданной части и проценту необходимо найти сам процент в единичном выражении. Для этого от 100% нужно отнять заданный процент, затем разделить заданное число на полученный процент и найти значение 1%. Умножив его на первоначальный процент, найдем искомую величину.

Пример: Сотрудником была получена зарплата в размере 40000 рублей. Эта сумма является остатком заработной платы по договору после вычета 13% подоходного налога. Необходимо найти размер подоходного налога в денежном выражении, вычтенного из зарплаты.

Решение: Заработная плата, выданная сотруднику, составляет 100%-13%=87%. Один процент от 40000 рублей составляет 40000/87=459.77 рубля. Тогда 13% будут равны 459.77×13=5977.01 рублей.

По правилам, чтобы высчитать какой-либо процент от числа, следует само число разделить на 100, а полученный результат умножить на количество процентов. К примеру, заработная плата сотрудника в месяц составила 25000, то 13% подоходного налога от этой суммы составит: 25000/100*13=3250. Многие пользователи офисной программы MS Excel знают, что в ней можно также высчитать необходимый процент. Для этого вам нужно набрать следующую комбинацию знаков: =N*n% и нажать Enter, где N– число, n– количество процентов. Например, чтобы посчитать, сколько будет 13% от 10000, стоит набрать в клетке: =10000*13% и нажать Enter. Появится ответ — 1300.

Аналогичным способом считаются проценты на стандартном калькуляторе персонального компьютера. В случае, если ваш калькулятор имеет инженерный вид, откройте вкладку «Вид» и поставьте галочку «Обычный».

Каждый человек в своей жизни практически повседневно сталкивается с понятием процентов. Причем это касается не только получения процентного значения от одного числа, но и решения задачи, как посчитать процент от суммы чисел. В повседневной жизни и обиходе многие не обращают на это внимания, тем не менее все эти вычисления заложены в нас еще со школьной скамьи.

Что такое процент

Что касается понятия процентов, то его можно объяснить самым простым способом, не вдаваясь пока в основы математических вычислений. На самом деле процент представляет собой какую-то часть чего-то еще. Неважно, в каком показателе будет выражено соответствие процента по отношению к основному исходному источнику. Главное — понимать, что такое представление может быть в виде самого процента (%) или в виде дроби, которая в конечном итоге и определяет отношение процентной части к исходному варианту.

Использование процентов на практике

Как рассчитывать проценты, каждый из нас знает еще из школьного курса математики. В повседневной жизни мы сталкиваемся с процентными соотношениями чуть ли не каждую минуту. Любая хозяйка, готовя какое-то блюдо, использует рецептуру, в которой представлено именно процентное соотношение. Самый простой пример: берем полстакана молока… Это и есть математическая трактовка того, что представляет собой определенная часть по отношению к целой.

За основу абсолютно всех вычислений принято считать 100 процентов (100%) или единицу (1), если расчет будет производиться с использованием дробей. От этого и отталкиваются при вычислении какой-либо составляющей от начального показателя.

То же самое касается и вопроса о том, как посчитать процент от суммы, когда в качестве начального (100-процентного) показателя выступает не одно число, а несколько. Вариантов расчета здесь может быть достаточно много. Рассмотрим самые основные.

Вычисление процентов по пропорции

Сейчас мы не будем брать в расчет вычисление процентов с использованием тех же таблиц офисных программ типа Excel, которые делают это в автоматическом режиме при задании соответствующей формулы.

В некоторых случаях используется калькулятор, на котором можно задавать вычисление подобных действий. Но речь сейчас не об этом.

Рассмотрим наиболее распространенные способы вычислений, знакомые нам из школьного курса математики.

Простейшим и самым распространенным способом является решение пропорции.

В данном случае исходное число задается в виде 100 процентов (скажем, некое произвольное число «a»), а его часть (допустим, «b») — в виде неизвестной «x». В математике это выглядит так:

Исходя из правил пропорции, можно вычислить неизвестное число x. Для этого используется так называемый перекрестный метод. Иными словами, нужно умножить b на 100 и разделить на a. Точно такое же правило действует, если в случае составления пропорции поменять b и x местами, когда процент известен, а нужно вычислить часть в числовом выражении.

Быстрое вычисление процентов

Конечно, вычисление процентов при помощи пропорции является фундаментальным. Однако с применением дробных чисел это процедура упрощается до невозможности. Ведь что такое 50% на самом деле? Половина. То есть 1/2 или 0,5 (исходя из начального числа 1). Теперь понятно: чтобы вычислить половину, нужно умножить искомое число или на 1/2, или на 0,5 либо разделить на 2. Такой способ, правда, годится только для чисел, которые делятся без остатка.

В случае возникновения остатка или бесконечных знаков в периоде после запятой типа 0,33333333… лучше использовать дробные выражения наподобие 1/3. Кстати, именно дроби (в некоторых случаях иррациональные) со всей точностью отражают само число, ведь периодические цифры после запятой, сколько ни задавай, все равно целого числа не дадут. А так та же одна треть четко и понятно выражает саму суть.

В тех же рецептах, естественно, треть можно определить, так сказать, на глаз. А вот в химических процессах, особенно связанных с тонкой дозировкой компонентов, скажем, в фармацевтике, такой метод не подойдет. Здесь на глаз полагаться не приходится. Необходимо использовать точные соотношения ингредиентов, даже если один из показателей имеет вид числа с цифрой в периоде или представлен в виде той же иррациональной дроби. Но, как правило, к примеру при взвешивании, такие числа могут ограничиваться после запятой десятитысячными или максимум стотысячными.

Как рассчитать процент от суммы

Очень часто приходится сталкиваться с несколькими искомыми числами или их суммой. Вопрос о том, как расчитывать проценты от суммы, решается так же просто, как и в случае использования одного начального числа. Единственное, что нужно учесть в этом случае, так это обычное представление суммы в виде единого значения.

Например, у нас имеется два числа, a и b, и начальным показателем выступает число d. В данном случае пропорция будет выглядеть следующим образом:

Заметьте, сумму (a + b) все равно можно представить в виде единого числа. Пускай это будет z. В случае, когда мы задаем формулу a + b = z, пропорция приобретает совершенно стандартный вид:

Как видим, ничего сложного в этом нет.

Есть и другой вариант, когда сумма (a + b) = 100%, а d = x.

Тут решение выглядит так:

(d x 100)/(a + b) или (d/(a + b)) + 100/(a + b).

Как уже понятно, здесь используется принцип общего знаменателя для дробей.

Если сложить a и b, сумма которых равна z, то пропорция опять возвращается к стандартному виду:

То же применяется и в обратном порядке.

Математическое объяснение

С точки зрения математики и ее основ решение задачи о том, как рассчитать процент от суммы, сводится только к применению простейших правил раскрытия скобок при умножении суммы на единое число и поиска общего знаменателя, который, в общем-то, им и является. Другими словами, представить в формульном выражении это можно так:

где ab и ac — произведения слагаемых в скобках (b и c) на число (коэффициент) перед скобками a.

Собственно, в пропорции действует тот же метод. Допустим, у нас есть некое число z, представляющее собой 100%, и сумма чисел a и b. Процент, который нужно вычислить, обозначим неизвестным числом y. В таком варианте пропорция принимает вид:

Отсюда простое решение:

((a + b) x 100%)/z = ((a x 100%) + (b x 100%))/z

В скобки действия взяты для того, чтобы подчеркнуть, что операции умножения выполняется в первую очередь, а сложение произведений — во вторую. Такое же действие производится, если изначально сумма чисел составляет 100%.

Обратное вычисление

Очень часто в вопросе о том, как посчитать процент от суммы, возникает и недвусмысленный обратный перевод. На практике это связано, скажем, с обратным вычислением четверти. Всем известно, что этот показатель составляет 25% от начального числа. Пусть, например, цену товара увеличили на 25%, что составило 25 рублей. Нужно найти, сколько стал стоить данный товар. Вот теперь попробуем разобраться, как вычислить не первоначальное число, зная значение процента, а всю сумму, которая должна получиться в конечном итоге. Казалось бы, решение простое:

Нет, абсолютно неверно. Так можно получить только изначальное число, без учета 25%. Для расчета всей суммы с учетом 25% нужно использовать формулу:

Или 100/0,8, что и покажет значение 125 (100 + 25), поскольку 100% плюс 25% в выражении единицы является числом 1,25 (единица плюс четвертая часть), а в обратном виде (1/x) — это именно 0,8. Произведя вычисления, получим, что х = 125.

Заключение

Как видим, ничего особо сложного в том, как посчитать процент от суммы, нет. Правда, в школьной программе обратный перевод почему-то зачастую опускается. Потом у многих бухгалтеров, работающих над отчетами с оплатой того же НДС, очень часто возникают проблемы.

Так что стоит просто учесть основные правила вычисления процентов, и проблемы исчезнут сами собой.

С другой стороны, для удобства можно применять в равной степени как пропорции, так и использование дробей. В первом случае мы имеем, так сказать, классический вариант, а во втором — простое и универсальное решение. Опять же его лучше использовать в случае деления без остатка. Зато при вычислении наиболее популярных долей типа половины, четверти, трети и т. д. такой метод является очень удобным.

Обратные вычисления, как видно из вышеприведенных примеров, тоже чем-то сложным не являются. Главное — учесть обратный коэффициент при расчете искомого числа. Думается, теперь все встало на свои места. Как говорится, простая математика.

Довольно часто перед нами встает такая задача, как посчитать процент от числа. В нашу жизнь прочно вошли такие понятия, как банковские проценты на вклад и кредит.

В выпусках новостей часто говорят о росте ВВП или пенсий на сколько-то процентов. Ребенок просит помочь с задачей, в которой необходимо вычислить процент доли химических элементов. Жизнь заставляет разобраться, что такое процентное отношение и как его считать.

От слова «цент», означающего число «сто», произошло множество известных слов. Сам «цент» — сотая часть доллара, «евроцент» — сотая часть евро. Слово «центнер» означает 100 кг. Знатоки истории вспомнят про центуриона, или сотника, в Древнем Риме.

Процент — слово, имеющее тот же корень, означает сотую часть какого-либо числа. Зачастую приходится сравнивать несколько чисел между собой, определить их соотношение. При этом удобней иметь дело не с целым числом, а какой-то долей.

Причем если все вышеназванные слова описывают зафиксированные величины, то наша величина может означать абсолютно разные вещи.

В каждом отдельном случае процент рассчитывается для конкретной величины и имеет с ней одинаковую размерность.

Например, проценты от некой суммы рублей будут измеряться в рублях. А процентная доля работ, измеряемых в кубометрах, тоже будет составлять сколько-то кубометров.

Простой способ расчета

Если вам необходимо выяснить величину одного процента от числа, просто передвиньте запятую в нем на два знака влево.

То есть 1% от 124 будет составлять 1,24; 1% от 81 — 0,81; 1% от 4,4 — 0,044.

В случае когда вам нужно вычислить число, составляющее какое-либо количество процентов от другого известного вам числа, стоит поступить так: известную вам величину необходимо умножить на интересующее вас процентное число, а затем разделить на сто.

Например, вычисляем 57% от 95:

95*57/100=54,15. Или 132% от 5483 составляет 5483*132/100=7237,56.

Пользуясь подобными несложными вычислениями, можно посчитать суммы, которые придется платить по кредиту или получать по вкладу.

Калькулятор и компьютерные программы

Некоторые люди и в школе не совсем уверенно чувствовали себя при необходимости вычислений в столбик, а по прошествии нескольких лет благополучно забыли, как это делается. Им на помощь придет калькулятор. Для нашей операции не потребуется серьезный инженерный калькулятор с множеством функций. Достаточно обычного, который есть в каждом телефоне.

Рассчитать процент на нем несложно. Набираем исходную величину, нажимаем знак «умножить», затем набираем нужное нам количество процентов и нажимаем знак «%». Допустим, есть необходимость высчитать долю оклада, уходящую на налоги. Размер оклада — 30000 рублей, налоги составляют 13%. Берем калькулятор и набираем следующую комбинацию:

30000*13%. Получаем 3900 рублей.

В любой компьютерной программе, например в «Экселе», посчитать проценты не составит труда. Если человек смог освоить такую серьезную программу, с помощью которой можно проводить расчеты любой сложности, то для него будет несложно провести такую элементарную операцию, как расчет процента числа в Excel.

Рассмотрим, как в «Экселе» посчитать процентную долю. В столбец В заносится исходное число, в столбец С — нужное нам количество процентов. В столбец D вносим выражение =C1/B1. После этого нажимается команда «процентный формат». В столбце D появится искомое число. Причем командами «увеличить разрядность» или «уменьшить разрядность» можно довести ответ до нужного нам уровня точности изменением количества знаков после запятой.

Способов, как посчитать процент от числа, много, они разнообразны, и человек с любым уровнем математической подготовки может выбрать для себя наиболее подходящий. Освоив разные методы, вы сможете помочь ребенку при решении задач. Причем не только в математике, но и в других науках. Например, в химии довольно часто приходится находить объемную или массовую долю элемента в веществе или растворе.

Владение вышеописанными навыками поможет вам осознанно подходить к вопросам, связанным с вашим семейным бюджетом. Высчитать процент расходов и сопоставить их с доходами — важнейшая операция для грамотного ведения домашнего хозяйства.

Используя калькулятор процентов Вы сможете производить всевозможные расчеты с использованием процентов. Округляет результаты до нужного количества знаков после запятой.

Сколько процентов составляет число X от числа Y. Какое число соответствует X процентам от числа Y. Прибавление или вычитание процентов из числа.

Источник