что такое обратные тригонометрические функции

Обратные тригонометрические функции, их графики и формулы

Определение обратных тригонометрических функций

Если особо не оговорено, то под обратными тригонометрическими функциями имеют в виду их главные значения, которые определяются следующими определениями.

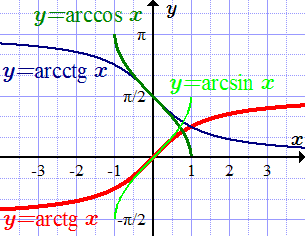
Графики обратных тригонометрических функций

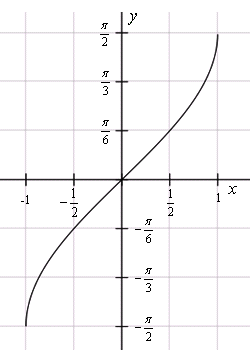
y = arcsin x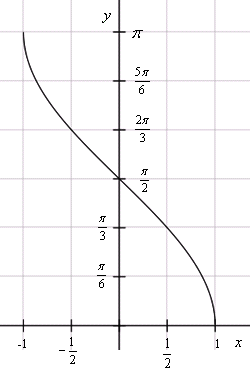
y = arccos x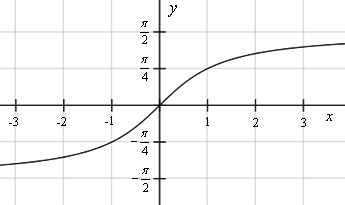
y = arctg x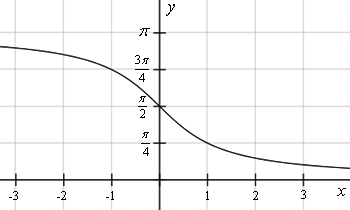
y = arcctg x

Основные формулы

Здесь следует особо обратить внимание на интервалы, для которых справедливы формулы.

arcsin(sin x ) = x при
sin(arcsin x ) = x
arccos(cos x ) = x при
cos(arccos x ) = x

arctg(tg x ) = x при
tg(arctg x ) = x
arcctg(ctg x ) = x при
ctg(arcctg x ) = x

Формулы, связывающие обратные тригонометрические функции

Формулы суммы и разности

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Источник

Основные тригонометрические тождества, их формулировки и вывод

В этой статье мы разберем такие важные понятия в тригонометрии, как арксинус, арккосинус, арктангенс и арккотангенс. Мы можем найти значения чисел (углов), если знаем данные тригонометрических функций; это и есть та самая задача, что приводит нас к обратным функциям.

Ниже мы не только дадим определения основных понятий и общепринятые обозначения, но и приведем расчеты, из которых будет ясно, что они из себя представляют. В конце мы попробуем связать понятия арккотангенса, арктангенса, арккосинуса и арксинуса с понятием единичной окружности.

Основные определения

Арксинус и другие обратные функции как угол

Сформулируем основные определения.

Вышеуказанные определения можно сформулировать в более краткой и символической форме:

Если вы хотите более подробно изучить такой подход к определению обратных тригонометрических функций, рекомендуем вам учебник Кочеткова (ч.1, стр. 260-278)

Арксинус и другие обратные функции как число

В том случае, если в задаче речь идет, скажем, о синусе угла, то логично его арксинус также воспринимать как угол. Если нам нужно, например, вычислить косинус некоторого числа, то тут важно встать на другую точку зрения и рассмотреть обратные функции как числа. Исходя из второго подхода, можно немного переформулировать определения:

Такие формулировки типичны для большинства современных учебников по математике.

Объяснение обратных функций с позиции геометрии

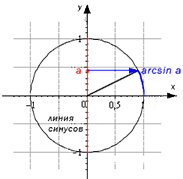
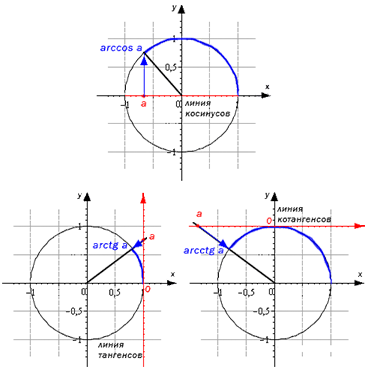
Более наглядно представить обратные функции числа можно геометрически: ведь если это углы, их можно изобразить на чертеже. Это просто сделать, если вы еще не забыли базовые определения основных прямых функций.

Для этого нам понадобится уже знакомая нам единичная окружность. Ее дуги, связывающие между собой основные углы, и будут соответствовать величинам обратных функций.

Вывод: что такое аркфункции

Источник

Арксинус, арккосинус, арктангенс и арккотангенс числа: основные свойства

Синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса

Это свойство используется чаще всего, поэтому логичнее всего начать рассмотрение всех основных свойств именно с него. Рассмотрим, чему равны синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса числа.

Синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса числа

Данное свойство следует напрямую из определения арксинуса, арккосинуса, арктангенса и арккотангенса.

sin ( a r c sin a ) = a

Доказательство для арккосинуса, арктангенса и арккотангенса строится аналогично, на базе определений этих функций. Вот несколько примеров использования данного свойства.

Пример 1. Свойства обратных тригонометрических функций

Арксинус, арккосинус, арктангенс и арккотангенс противоположных чисел

Существует связь между арксинусами, арккосинусами, арктангенсами и арккотангенсами противоположных чисел. Запишем соотношения, выражающие ее.

arcsin, arccos, arctg и arcctg противоположных чисел

Доказательство свойства арксинусов противоположных чисел завершено.

Теперь рассмотрим доказательство свойства арккосинусов противоположных чисел.

Доказательства для арктангенса и арккотангенса проводится по аналогичному принципу.

Сумма арксинуса и арккосинуса, арктангенса и арккотангенса

Данное свойство устанавливает связь соответственно между арксинусом и арккосинусам, арктангенсом и арккотангенсом. Запишем формулы для арксинуса и арккосинуса.

Сумма arcsin и arccos

Соответственно, для арктангенса и арккотангенса

Сумма arctg и arcctg

Пользуясь разобранными свойствами, можно выряжать арксинус через арккосинус, арккосинус через арксинус, арктангенс через арккотангенс и наоборот.

Пример 2. Сумма арксинуса и арккосинуса

Арксинус синуса, арккосинус косинуса, арктангенс тангенса и арккотангенс котангенса

Запишем соотношения, иллюстрирующие свойства арксинуса синуса, арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса.

Свойства арксинуса синуса, арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса

Аналогично, соблюдение условий обязательно для арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса.

К примеру, запись a r c sin ( sin 8 π 3 ) = 8 π 3 будет ошибочной, так как число 8 π 3 не удовлетворяет условиям неравенства.

Описанные в этой статье свойства позволяют получить ряд полезных формул, определяющих связи между основными и обратными тригонометрическими функциями. Соотношениям, связывающим sin, cos, tg, ctg, arcsin, arccos, arctg и arcctg будет посвящена отдельная статья.

Источник

Свойства обратных тригонометрических функций

Так как геометрически значение обратной тригонометрической функции связано с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку, то названия обратных тригонометрических функций образуются следующим образом: приставка «арк-» (от латинского arc — дуга) + соответствующие им названия тригонометрических функций.

Арксинус

Арксинусом числа \( a \) называется такое значение угла \( \alpha, \) для которого \( \sin \alpha=a,\;|a|\leqslant 1,\;\alpha\in[-\frac<\pi><2>;\frac<\pi><2>]. \)

Арккосинус

Арккосинусом числа \( a \) называется такое значение угла \( \alpha, \) для которого \( \cos \alpha=a,\;|a|\leqslant 1,\;\alpha\in[0;\pi]. \)

Арктангенс

Арктангенсом числа \( a \) называется такое значение угла \( \alpha, \) для которого \( \text\, \alpha=a,\;a\in\mathbb,\;\alpha\in\left (-\frac<\pi><2>;\frac<\pi> <2>\right ). \)

Арккотангенс

Арккотангенсом числа \( a \) называется такое значение угла \( \alpha, \) для которого \( \text\, \alpha=a,\;a\in\mathbb,\;\alpha\in\left (0;\pi \right ). \)

Основные соотношения

Решение простейших тригонометрических уравнений

\( \sin x=a,\;|a|\leqslant 1\Rightarrow x=(-1)^k\arcsin\,a+\pi k,\;k\in\mathbb \)

\( \cos x=a,\;|a|\leqslant 1\Rightarrow x=\pm\arccos\,a+2\pi k,\;k\in\mathbb \)

\( \text\, x=a,\;a\in\mathbb\Rightarrow x=\text\,a+\pi k,\;k\in\mathbb \)

Частные случаи

\( \sin x=0\Rightarrow x=\pi k,\;k\in\mathbb \)

\( \cos x=0\Rightarrow x=\frac<\pi><2>+\pi k,\;k\in\mathbb \)

\( \text\, x=0\Rightarrow x=\pi k,\;k\in\mathbb \)

\( \sin x=1\Rightarrow x=\frac<\pi><2>+2\pi k,\;k\in\mathbb \)

\( \cos x=1\Rightarrow x=2\pi k,\;k\in\mathbb \)

\( \sin x=-1\Rightarrow x=-\frac<\pi><2>+2\pi k,\;k\in\mathbb \)

\( \cos x=-1\Rightarrow x=\pi+2\pi k,\;k\in\mathbb \)

Источник

ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ,

аркфуикции, круговые функции,- функции, обратные тригонометрическим функциям. Шести основным тригонометрич. функциям соответствуют шесть О. т. ф.: арксинус, арккосинус, арктангенс, арккотангенс, арксеканс, арккосеканс; обозначаются соответственно Arc sin х,Arc cos x,Arc tg x,Arc ctg x,Arc sec x,Arc cosec x. Функции Arc sin xи Arc cos xопределены (в действительной области) для 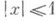, функции Arc tg x и Arc ctg x- для всех действительных х, а функции Arc sec xи Arc cosec x- для ; две последние функции малоупотребительны. Другие обозначения: и т. п.

О. т. ф. связаны соотношениями

Поэтому функции 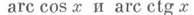в нижеследующих формулах не фигурируют.

О. т. ф. бесконечно дифференцируемы и в окрестности каждой внутренней точки своей области определения могут быть разложены в ряды Тейлора. Производные, интегралы и разложения в ряды О. т. ф.:

О. т. ф. комплексного переменного определяются как аналитические продолжения соответствующих О. т. ф. действительного переменного в комплексную плоскость.

О. т. ф. выражаются через логарифмическую функцию:

Полезное

Смотреть что такое «ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ,» в других словарях:

ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ — функции, обратные тригонометрическим (см.). Функцией, обратной синусу, является арксинус, функцией, обратной косинусу, является арккосинус и т. д. Обозначаются так: Arcsin x (арксинус x), Arccos x (арккосинус x) и т.д … Большая политехническая энциклопедия

ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ — общее название функций арксинуса, арккосинуса, арктангенса, арккотангенса, арксеканса, арккосеканса, каждая из которых выражает величину дуги (или угла), соответствующей данному значению х тригонометрической функции, название которой получается… … Большой Энциклопедический словарь

Обратные тригонометрические функции — (круговые функции, аркфункции) математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций: арксинус (обозначение: arcsin) арккосинус (обозначение: arccos)… … Википедия

Обратные тригонометрические функции — аркфункции, круговые функции, решают следующую задачу: найти дугу (число) по заданному значению её тригонометрической функции. Шести основным тригонометрическим функциям соответствуют шесть О. т. ф.: 1) Arc sin х («арксинус x») функция,… … Большая советская энциклопедия

обратные тригонометрические функции — общее название функций арксинуса, арккосинуса, арктангенса, арккотангенса, арксеканса, арккосеканса, каждая из которых выражает величину дуги (или угла), соответствующей данному значению х тригонометрической функции, название которой получается… … Энциклопедический словарь

ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ — функции, обратные тригонометрическим функциям. Обычно рассматривают следующие О. т. ф.: Arcsin х (арксинус х) ф ция, обратная sin х; Arccos х (арккосинус х) ф ция, обратная cos Л; Arctg х (арктангенс х) ф ция, обратная tg х; Arcctg х… … Большой энциклопедический политехнический словарь

ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ — общее назв. функций арксинуса, арккосинуса, арктангенса, арккотангенса, арксеканса, арккосеканса, каждая из к рых выражает величину дуги (или угла), соответствующей данному значению х тригонометрич. функции, название к рой получается… … Естествознание. Энциклопедический словарь

Обратные гиперболические функции — Обратные гиперболические функции определяются как обратные функции к гиперболическим функциям. Эти функции определяют площадь сектора единичной гиперболы x2 − y2 = 1 аналогично тому, как обратные тригонометрические функции определяют длину… … Википедия

Тригонометрические функции — Запрос «sin» перенаправляется сюда; см. также другие значения. Запрос «sec» перенаправляется сюда; см. также другие значения. Запрос «Синус» перенаправляется сюда; см. также другие значения … Википедия

Тригонометрические функции — один из важнейших классов элементарных функций. Для определения Т. ф. обычно рассматривают окружность единичного радиуса с двумя взаимно перпендикулярными диаметрами A A и B B (рис. 1). От точки А по окружности откладываются дуги … Большая советская энциклопедия

Источник