что такое обобщенная задача высокого уровня
Обобщенная задача в системе личностно ориенторованного обучения
Автор работы: Пользователь скрыл имя, 16 Мая 2012 в 14:45, курсовая работа
Краткое описание
Целью данной работы является определить преимущества обобщенных задач, проанализировать возможность их применения в современной школе, а также разработать примеры математических задач развивающего типа.
Задачами является выявление особенностей личностно ориентированного образования, обоснование значимости обобщенных задач, разработка примеров задач обобщенного типа по математике для учащихся 7 класса.
Содержание
Глава 1. Теоретико-методический анализ личностно
Глава 2. Обобщенная задача в системе личностно
Глава 3. Обобщенные задачи по математике с использованием
Глава 4. Примеры обобщенных задач
Список использованной литературы.
Вложенные файлы: 1 файл
введение.docx
В процессе разработки и апробации системы обобщенных задач был определен алгоритм их проектирования, который включает следующие этапы деятельности преподавателя:
– анализ и отбор собственно предметного содержания учебного материала;
– поиск и выявление межпредметных связей, наполнение содержания задачи ценностной, социально-педагогической, прикладной, фактологической составляющими;
– формулировка вопросов и заданий, направленных на активизацию рефлексивно-оценочной деятельности обучающихся и использование их субъектного опыта;
– разработка текстовой, графической, табличной форм представления учебного материала при постановке задач;
– моделирование возможных ролевых позиций, которые обучающиеся могут занимать в процессе решения задач;
– предварительный анализ возможных альтернативных способов решения задачи.
Конструирование содержания обобщенных задач по математике осуществляется на основе уровневого подхода. Обобщенные задачи с точки зрения их влияния на развитие у школьников компетенций можно классифицировать по трем уровням:
Основанием для выявления названных уровней является степень овладения школьником математических знаниями, сформированности у них соответствующих обобщенных умений и навыков применения математических знаний и опыта для решения социально-профессиональных задач.
Критериями при выставлении баллов за решение обобщенных задач могут выступать:
Обобщенная задача предполагает несколько ответов. При этом допускается ситуация, когда с точки зрения отвечающего вопрос в задаче поставлен некорректно или мнение школьника не совпадает с позицией разработчиков задачи. В этом случае позиция школьника-оппонента должна быть обоснована в соответствии с научно-педагогическими смыслами, а не с бытовыми знаниями; приведены контр-примеры.
Подведя итог вышеизложенному, можно сделать вывод, что внедрение в обучение обобщенных задач позволит не только с легкостью закреплять материал по математике, но и повысит знания в других областях, а применение интересных фактов, цифр и информации при проектировании и создании обобщенных задач поможет сформировать интерес к математике в целом и осознание значимости и социальной ориентированности данного предмета.
Глава 3. Обобщенные задачи по математике с использованием информационных технологий
Обобщенные задачи по математике с использованием информационных технологий – это задачи поисково-исследовательской направленности, решение и представление результатов которых предполагают применение информационных ресурсов и технологий; при этом их условия дополнены методическими указаниями и рекомендациями. Последние могут включать описание способов самопроверки, критериев правильности решения, типичных ошибок, что позволит школьникам перейти от деятельности по образцу к самостоятельному конструированию решения.
Важнейшими характеристиками, которые необходимо учитывать при разработке и использовании таких задач в учебном процессе, выступают следующие:
В результате решения задач поисково-исследовательской направленности у школьников развиваются способы теоретического, творческого мышления, признаками которых являются способность к целеполаганию, проектированию и конструированию, переносу или моделированию методов решения задач; они приобретают навыки системного анализа, умений прогнозировать как ближайшие, так и отдаленные последствия деятельности, соотносить их с поставленными целями. Названные умения и навыки составляют основу ряда ключевых компетенций, способствующих эффективному самообразованию школьников, исследовательской деятельности.
Разработка и применение в учебном процессе обобщенных задач с использованием информационных технологий позволяет выделить их следующие особенности:
Обобщенные задачи с использованием компьютерных технологий можно разделить на следующие:
1. Задачи-проекты с использованием технологии представления отчетных материалов Web-квест (задача предназначается и для групповой разработки)
Пример задания: создайте Web-сайт, на страницах которого отражается процесс и результат выполнения проекта по любой математической теме.
Методические указания для школьников. Сайт содержит страницы, созданные самими обучающимися в процессе проведения исследования, а также Интернет-ссылки на работы, базы данных, Интернет-журналы, виртуальные музеи и т.д., которые логически связаны разрабатываемой в рамках проекта проблемой.
Кроме этого сайт включает следующие разделы:
– вступление, в котором описываются проблема, план работы над ней, роли участников проекта;
– основное задание, которое должны выполнить участники;
– список информационных ресурсов;
– описание процедуры работы;
– полученные выводы и заключение.
Для эффективного выполнения такого рода заданий для школьников должны быть предварительно подготовлены электронные формы различных документов-отчетов.
Предполагается, что создавать Web-сайты школьники могут любыми доступными для них средствами, в том числе и с помощью MS Word.
2. Проекты научно-популярного журнала с использованием MS PowerPoint
Пример задания: разработать проект научно-популярного журнала по межпредметной тематике и создать систему динамических презентаций, используя возможности MS PowerPoint.
Например, журнал может иметь название «Математика в жизни», а работа по его созданию отражает связь жизни с математикой.
Методические указания для школьников. При создании проекта журнала руководствуйтесь следующими критериями оценки проекта:
При подготовке презентации обратите внимание на создание образности и структурированности представляемой информации. Этого можно добиться через использование визуального представления содержания с помощью схем, рисунков, таблиц и графиков. Слайд не должен быть перенасыщен текстом, который в противном случае будет тяжело читаться. При выборе оформления презентации и создании эффектов старайтесь, чтобы они не отвлекали внимание от содержания (именно поэтому в большинстве случаев рекомендуется использовать светлый фон и темный цвет шрифта и не злоупотреблять анимацией).
Примерами схем, реализованных в MS PowerPoint при подготовке подобного вида заданий, могут выступать следующие:
3. Задания по разработке тестов в электронном виде
Пример задания: Разработайте по любой из тем дисциплины «Математика» электронные формы для разных тестовых заданий: на узнавание: альтернативные, на различение, на установление соответствия, на установление правильной последовательности; на воспроизведение по памяти: на дополнение с ограничением ответа (подстановка); на воспроизведение на уровне понимания и применения знаний в знакомой ситуации: на свободно конструируемый ответ, на соответствие, типовая задача.
При оценивании задания учитываются: правильность работы электронной формы, удобство ее использования, а также содержание вопросов теста (их корректность, актуальность, научность, нестандартность, исследовательский уровень, межпредметный характер).
4. Задание по разработке гипертекстового учебного пособия
Пример задания: Разработать проект гипертекстового учебного пособия по математической теме (ам).
Выполнение данного задания способствует развитию у школьников следующих умений: анализировать учебный материал, структурировать его нужным образом, выделять главные и второстепенные его идеи; определять взаимосвязи между составляющими частями содержания.
Критерии оценки проекта:
Подведя итог вышесказанному, можно сделать выводы, что применение информационных технологий способствует отличному закреплению изучаемого материала, развивает способы теоретического, творческого мышления; школьники приобретают навыки системного анализа. Кроме того прослеживается тесная связь математики и информатики. Подобные задачи служат игровой формой, стимулирующей познавательные процессы и интересы школьников.
Обобщённая задача о назначениях
Связанные понятия
Модели дискретного выбора — экономические (эконометрические) модели, позволяющие описывать, объяснять и прогнозировать выбор между, двумя или более альтернативами (то есть когда множество альтернатив не более чем счетно). Модели дискретного выбора позволяют на основе некоторых характеристик (атрибутов) экономического субъекта или ситуации оценить вероятность выбора той или иной альтернативы.
Функция предельного правдоподобия (англ. Marginal Likelihood Function) или интегрированное правдоподобие (англ. integrated likelihood) — это функция правдоподобия, в которой некоторые переменные параметры исключены. В контексте байесовской статистики, функция может называться обоснованностью (англ. evidence) или обоснованностью модели (англ. model evidence).
Важнейшими с точки зрения приложений характеристических функций к выводу асимптотических формул теории вероятностей являются две предельные теоремы — прямая и обратная. Эти теоремы устанавливают, что соответствие, существующее между функциями распределения и характеристическими функциями, не только взаимно однозначно, но и непрерывно.
В статистике метод оценки с помощью апостериорного максимума (MAP) тесно связан с методом максимального правдоподобия (ML), но дополнительно при оптимизации использует априорное распределение величины, которую оценивает.
Эллиптические уравнения — класс дифференциальных уравнений в частных производных, описывающих стационарные процессы.
Логика сознания. Часть 10. Задача обобщения

Взаимодействие с окружающим миром приводит к накоплению опыта. Если в этом опыте есть какие-либо закономерности, то они могут быть выделены и впоследствии использованы. Наличие закономерностей можно интерпретировать, как присутствие чего-то общего в воспоминаниях, составляющих опыт. Соответственно, выделение таких общих сущностей принято называть обобщением.
Задача обобщения – это ключевая задача во всех дисциплинах, которые хоть как-то связаны с анализом данных. Математическая статистика, машинное обучение, нейронные сети – все это вращается вокруг задачи обобщения. Естественно, что и мозг не остался в стороне и как мы можем иногда наблюдать на собственном опыте, тоже порой неплохо справляется с обобщением.
Несмотря на то, что обобщение возникает всегда и везде сама задача обобщения, если рассматривать ее в общем виде, остается достаточно туманной. В зависимости от конкретной ситуации в которой требуется выполнить обобщение постановка задачи обобщения может меняться в очень широком диапазоне. Различные постановки задачи порождают очень разные и порой совсем непохожие друг на друга методы решения.
Многообразие подходов к обобщению создает ощущение, что процедура обобщения – это нечто собирательное и что универсальной процедуры обобщения, видимо, не существовует. Однако, мне кажется, что универсальное обобщение возможно и именно оно и свойственно нашему мозгу. В рамках описываемого в этом цикле подхода удалось придумать удивительно красивый (по крайней мере мне он кажется таким) алгоритм, который включает в себя все классические вариации задачи обобщения. Этот алгоритм не только хорошо работает, но и самое удивительное — он идеально ложится на архитектуру биологических нейронных сетей, что заставляет верить, что, действительно, где-то так работает и реальный мозг.
Перед тем как описывать алгоритм такого универсального обобщения попробуем разобраться с тем какие формы обобщения принято выделять и, соответственно, что и почему должен включать в себя универсальный подход.
Философско-семантический подход к обобщению понятий
Философия имеет дело с семантическими конструкциями. Проще говоря, выражает и записывает свои утверждения фразами на естественном языке. Философско-семантический подход к обобщению заключается в следующем. Имея понятия, объединенные неким видовым признаком, требуется перейти к новому понятию, которое дает более широкое, но менее конкретное толкование, свободное от видового признака.
Например, имеется понятие «наручные часы», которое описывается как: «указатель времени, закрепленный на руке с помощью ремешка или браслета». Если мы избавимся от видового признака «закрепленный на руке…», то получим обобщенное понятие «часы», как любой инструмент, определяющий время.
В примере с часами в самом названии наручных часов содержалась подсказка для обобщения. Достаточно было отброс ить лишнее слово и получалось требуемое понятие. Но это не закономерность, а следствие семантики, построенной «от обратного», когда нам уже известен результат обобщения.
Задача чистого обобщения
В формулировке Френка Розенблатта задача чистого обобщения звучит так: «В эксперименте по «чистому обобщению» от модели мозга или персептрона требуется перейти от избирательной реакции на один стимул (допустим, квадрат, находящийся в левой части сетчатки) к подобному ему стимулу, который не активирует ни одного из тех же сенсорных окончаний (квадрат в правой части сетчатки)» (Rosenblatt, 1962).
Акцент на «чистое» обобщение подразумевает отсутствие «подсказок». Если бы нам предварительно показали квадрат во всех возможных позициях сетчатки и дали возможность все это запомнить, то узнавание кадрата стало бы тривиальным. Но по условию квадрат нам показали в одном месте, а узнать мы должны его совсем в другом. Сверточные сети решают эту задачу за счет того, что в них изначально заложены правила «перетаскивания» любой фигуры по всему пространству сетчатки. За счет знания того как «перемещать» изображение они могут взять квадрат, увиденный в одном месте и «примерить» его ко всем возможным позициям на сетчатке.
Поиск паттерна в форме буквы «T» в разных позициях изображения (Fukushima K., 2013)
Ту же задачу мы в нашей модели решаем за счет создания пространства контекстов. Отличие от сверточных сетей в том, кто к кому идет — «гора к Магомеду» или «Магомед к горе». В сверточных сетях при анализе новой картинки каждый предварительно известный образ варьируется по всем возможным позициям и «примеряется» к анализируемой картинке. В контекстной модели каждый контекст трансформирует (перемешает, поворачивает, масштабирует) анализируемую картинку так как ему предписывают его правила, а затем «сдвинутая» картинка сравнивается с «неподвижными» заранее известными образами. Эта, на первый взгляд, небольшая разница дает последующее очень сильное различее в подходах и их возможностях.
Родственна задаче чистого обобщения задача инвариантного представления. Имея явление, предстающее перед нами в разных формах, требуется инвариантно описать эти представления с целью узнавания явления в любых его проявлениях.
Задача классификации
Есть множество объектов. Есть предварительно заданные классы. Есть обучающая выборка – набор объектов, про которые известно к каким классам они относятся. Требуется построить алгоритм, который обоснованно отнесет любые объекты из исходного множества к одному из классов. В математической статистике задачи классификации относят к задачам дискриминантного анализа.
В машинном обучении задача классификации считается задачей обучения с учителем. Есть обучающая выборка, про которую известно: какой стимул на входе приводит к какой реакции на выходе. Предполагается, что реакция не случайна, а определяется некой закономерностью. Требуется построить алгоритм, который наиболее точно воспроизведет эту закономерность.
Алгоритм решение задачи классификации зависит от характера входных данных и типов получаемых классов. О том, как решается задача классификации в нейронных сетях и как происходит обучение с учителем в нашей модели мы говорили в предыдущей части.
Задача кластеризации
Предположим у нас есть множество объектов и нам известна степень похожести их друг на друга, заданная матрицей расстояний. Требуется разбить это множество на подмножества, называемые кластерами, так, чтобы каждый кластер объединял схожие объекты, а объекты разных кластеров сильно отличались друг от друга. Вместо матрицы расстояний могут быть заданы описания этих объектов и указан способ, как искать расстояние между объектами по этим описаниям.
В машинном обучении, кластеризация попадает под обучение без учителя.
Кластеризация – очень соблазнительная процедура. Удобно разбить множество объектов на относительное небольшое количество классов и впоследствии использовать не исходные, возможно громоздкие описания, а описания через классы. Если при разбиении заранее известно какие признаки важны для решаемой задачи, то кластеризация может «делать акцент» на эти признаки и получать классы удобные для последующего принятия решений.
Однако, в общем случае ответ на вопрос о важности признаков лежит за пределами задачи кластеризации. Последующее обучение, называемое обучением с подкреплением, должно само, исходя из анализа того насколько удачно или нет оказалось поведение ученика, определить какие признаки важны, а какие нет. При этом «самыми удачными» признаками могут оказаться не признаки из исходных описаний, а уже обобщенные классы, взятые как признаки. Но для определения важности признаков надо, чтобы эти признаки уже присутствовали в описании на момент работы обучения с подкреплеием. То есть получается, что заранее неизвестно какие признаки могут оказаться важными, но понять это можно только уже имея эти признаки.
Другими словами, в зависимости от того какие признаки исходного описания использовать, а какие игнорировать при проведении кластеризации получаются различные системы классов. Одни из них оказываются более полезными для последующих целей, другие менее. В общем случае выходит, что хорошо бы перебрать все возможные варианты кластеризаций, чтобы понять какие из них наиболее удачны для решения конкретной задачи. Причем для решения другой задачи может оказаться удачной совсем другая система кластеризации.
Даже если мы решим на что стоит сделать акцент при кластеризации все равно останется вопрос об оптимальной детализации. Дело в том, что в общем случае нет априорной информации о том на сколько классов надо поделить исходное множество объектов.
Вместо знания о количестве классов можно использовать критерий, указывающий на то насколько точно должны все объекты соответствовать созданным классам. В этом случае можно начинать кластеризацию с некого начального количества классов и добавлять новые классы если остаются объекты, для которых ни один класс не подходит достаточно хорошо. Но процедура с добавлением не снимает вопроса оптимальности детализации. При задании низкого порога соответствия объекта классу получаются большие классы, отражающие основные закономерности. При выборе высокого порога получается много классов с небольшим числом объектов. Эти классы учитывают мелкие детали, но за деревьями становится не видно леса.
Факторный анализ
Предположим, что мы имеем множество объектов в котором все объекты снабжены признаковыми описаниями. Такие описания можно записать соответствующими векторами. Далее предположим, что признаки имеют количественную природу.
Удобно центрировать описания, то есть рассчитать среднее для каждого признака и скорректировать признаки на их среднее значение. Это равносильно переносу начала координат в «центр масс». Можно посчитать корреляции между признаками. Если записать корреляционную матрицу признаков и найти ее собственные вектора, то эти вектора будут являться новым ортогональным базисом, в котором можно описать исходное множество объектов.
В базисе из исходных признаков за счет их возможной коррелированности линейные закономерности были «размазаны» между признаками. При переходе к ортогональному базису начинает четче проступать внутренняя структура закономерностей. Так как ортогональный базис определен с точностью до вращения, то можно так повернуть базис из собственных векторов, чтобы направления осей наилучшим образом соответствовали тем направлениям, вдоль которых данные имеют наибольший разброс.
Собственные числа, соответствующие собственным векторам, показывают какой процент от общей дисперсии приходится на какой собственный вектор. Собственные вектора, на которые приходится наиболее существенный процент дисперсии называют главными компонентами. Часто бывает удобно перейти от описания в исходных признаках к описанию в главных компонентах.
Так как главные компоненты отражают наиболее существенные линейные закономерности, свойственные исходному множеству, то они могут называться определенным обобщением исходных данных.
Замечательное свойство факторного анализа — это то, что факторы могут не только напоминать исходные признаки, но и могут оказаться новыми ненаблюдаемыми сущностями.
Если сравнивать обобщения, которые получаются через классы и которые получаются через факторы, то условно можно сказать, что классы выделяют «области», а факторы – «направления».
Часто для отнесения объекта к классу смотрят не столько на близость объекта к центру класса, а на соответствие объекта параметрам распределения, свойственным классу (на этом, например, построен EM алгоритм). То есть если в пригороде города стоит тюрьма, то человек которого вы встретите рядом с тюрьмой скорее всего горожанин, а не заключенный, хотя расстояние до центра города значительно выше чем до центра тюрьмы. «Области» стоит понимать с учетом этого замечания.
Ниже приведена картинка, по которой можно приблизительно соотнести обобщение классами и факторами.
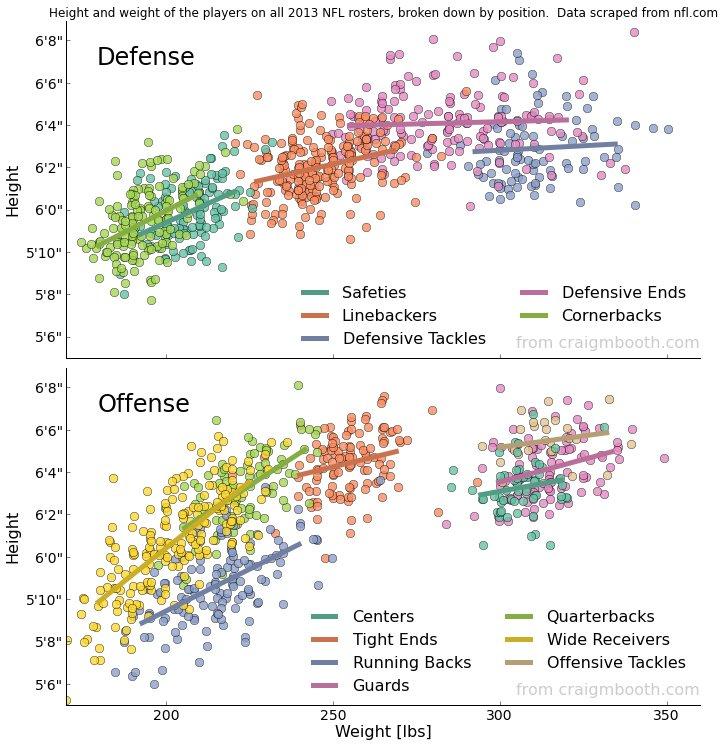
Графики распределения роста и веса игроков американской футбольной лиги (NFL). Сверху игроки защиты, снизу игроки нападения. Цветами выделены позиции игроков (Dr. Craig M. Booth).
Все множество игроков можно разбить на классы по их роли на поле. По параметрам «вес — рост» можно выделить глобальные факторы (не показаны) или факторы для каждого из классов.
Цветные линии соответствуют первому главному фактору в каждом из классов. Этот фактор можно интерпретировать как «размер игрока». Он определяется как проекция точки игрока на эту ось. Значение проекции дает значение, которое отбрасывает «не идеальность» игрока. Если к первой оси провести вторую ортогональную, то она будет описывать второй фактор «тип телосложения», проще говоря, худой игрок или толстый.
При всей красоте и удобстве факторов есть с ними и сложности. Так же, как и с классами всегда стоит вопрос сколько и каких факторов стоит выделять и использовать. Конечно, удобно, когда несколько первых главных компонент несут почти всю информацию, но на практике такое бывает нечасто. Например, возьмем 10 000 наиболее популярных фильмов, несколько миллионов человек и проанализируем оценки, которые они поставили тем фильмам, что посмотрели. Несложно составить корреляционную матрицу для фильмов. Положительная корреляция между двумя фильмами говорит о том, что люди, которые оценивают один фильм выше среднего скорее всего выше среднего оценивают и другой.
Проведем факторный анализ корреляционной матрицы и затем вращение осей для удобной интерпретации факторов. Окажется, что существенную роль играют первые пять-шесть факторов. Они соответствуют наиболее общим закономерностям. Это, конечно, жанры фильмов: «боевик», «комедия», «мелодрама». Кроме того, выделятся факторы: «русское кино» (если люди будут из России) и «авторское кино». Последующие факторы тоже можно интерпретировать, но их вклад в объяснение дисперсии будет все меньше и меньше.
Первые пять самых существенных факторов объясняют порядка 30 процентов общей дисперсии. Это не особо много, учитывая, что дисперсия – это квадрат среднеквадратического отклонения. Соответственно, основные факторы объясняют всего 17 процентов общего разброса оценок. Если посмотреть на остальные факторы, то многие из них объясняют всего лишь десятые или сотые доли процента общей дисперсии и вроде бы несущественны.
Но каждый мелкий фактор, как правило, соответствует некой локальной закономерности. Он объединяет фильмы одного режиссера, одного сценариста или одного актера. Оказывается, что когда мы хотим что-либо понять про конкретный фильм, то основные факторы объясняют свои 30 процентов дисперсии и при этом процентов 40-50 дисперсии объясняют один-два мелких фактора, которые несущественны для общей массы, но оказываются чрезвычайно важны именно для этого фильма.
Принято говорить, что «дьявол в деталях». Это относится именно к тому, что практически нет факторов, которыми можно пренебречь. Каждая мелочь может оказаться решающей в определенной ситуации.
Формирование понятий
Результатом обобщения может являться формирование понятий с использованием которых строятся последующие описания. Есть разные мнения относительно того, что является основным принципом, по которому человек выделяет те или иные понятия. Собственно, все пункты настоящего перечисления имеют к этому непосредственное отношение.
Задача идеализации
В процессе обобщения мы получаем понятия, которые по неким признакам объединяют множество явлений, с которыми мы ранее сталкивались. Выделение того общего, что есть в этих явлениях приводит к тому, что мы можем описать свойства неких идеальных понятий, свободных от индивидуальных деталей отдельных явлений.
Именно идеальные понятия лежат в основе математики. Точка, прямая, плоскость, число, множество – это идеализации объектов из нашего повседневного опыта. Математика вводит для этих понятий формальную систему правил, которая позволяет строить утверждения, преобразовывать эти утверждения, доказывать или опровергать их истинность. Но если для самой математики базовые понятия первичны, то для человека они связаны с опытом их использования. Это позволяет математикам не использовать полный перебор при поисках доказательств, а осуществлять более целенаправленный поиск, основанный на опыте, лежащем за идеальными понятиями.
Логическая индукция
Логическая индукция подразумевает получение общего закона по множеству частных случаев.
Разделяют полную индукцию:
И неполную индукцию:
Неполная индукция имеет дело с вероятностью и может быть ошибочной (проблема индукции).
Индукция связана с обобщением в двух моментах. Во-первых, когда говорится о множестве объектов, то подразумевается, что предварительно что-то послужило основанием объединить эти объекты в единое множество. То есть нашлись какие-то механизмы, которые позволили сделать предварительное обобщение.
Во-вторых, если мы методом индукции обнаруживаем некий признак, который свойственен элементам некой группы, которая описывает определенное понятие, то мы можем использовать этот признак, как характеризующий для отнесения к этой группе.
Например, мы обнаруживаем, что существуют механические приборы с характерным циферблатом и стрелками. По внешнему сходству мы делаем обобщение и относим их к классу часы, и формируем соответствующее понятие.
Далее мы замечаем, что часы могут определять время. Это позволяет нам сделать неполную индукцию. Мы заключаем, что свойство всех часов – способность определять время.
Теперь мы можем сделать следующий шаг обобщения. Мы можем сказать, что к «часам» можно отнести вообще все, что позволяет следить за временем. Теперь часами мы можем назвать и солнце, которое отмеряет сутки и школьные звонки, отсчитывающие уроки.
Логическая индукция имеет много общего с семантическим обобщением понятий. Но семантическое обобщение делает несколько иной акцент. Семантический подход говорит о признаках, которые составляют описание понятия, и возможности отбрасывания их части для получения более общей формулировки. При этом остается открытым вопрос — откуда должны взяться такие определения понятий, которые позволят выполнить переход к обобщению «через отбрасывание». Неполная логическая индукция как раз и показывает путь формирования таких описательных признаков.
Задача дискретизации
Имея дело с непрерывными величинами, часто требуется перейти к их описанию в дискретных значениях. Для каждой непрерывной величины выбор шага квантования определяется той точностью описания, которую требуется сохранить. Получившиеся в результате интервалы дробления объединяют различные значения непрерывной величины, ставя им в соответствие определенные дискретные понятия. Такую процедуру можно отнести к обобщению по тому факту, что объединение значений происходит, исходя из их попадания в интервал квантования, что говорит об их определенной общности.
Соотнесение понятий
Осуществляя обобщение любым из возможных способов, мы можем представить результат обобщения через систему понятий. При этом обобщенные понятия не просто образуют набор независимых друг от друга элементов, а приобретают внутреннюю структуру взаимоотношений.
Например, классы, получаемые в результате кластеризации, образуют некую пространственную структуру, в которой какие-то классы оказываются ближе друг к другу, какие-то дальше.
При использовании описания чего-либо через факторы используют набор факторных весов. Факторные веса принимают вещественные значения. Эти значения можно аппроксимировать набором дискретных понятий. При этом для этих дискретных понятий будет характерна система отношений «больше – меньше».
Таким образом, нас каждый раз интересует не просто выделение обобщений, но и формирование некой системы, в которой будет понятно, как эти обобщения соотносятся со всеми остальными обобщениями.
Чем-то похожая ситуация возникает при анализе естественного языка. Слова языка имеют определенные взаимосвязи. Природа этих связей может быть различна. Можно говорить о частоте совместного проявления слов в реальных текстах. Можно говорить о похожести их смыслов. Можно строить систему отношений, основанную на переходах к более общему содержанию. Подобные построения приводят к семантическим сетям разного вида.
Пример семантической сети (Автор: Знанибус — собственная работа, CC BY-SA 3.0, commons.wikimedia.org/w/index.php?curid=11912245)
Говорят, что в правильной постановке задачи содержится три четверти верного ответа. Очень похоже, что это справедливо и для задачи обобщения. Что мы хотим видеть результатом обобщения? Устойчивые классы? Но где границы этих классов? Факторы? Какие и сколько? Закономерности? Редкие, но сильные совпадения или нечеткие, но подкрепленные большим числом примеров зависимости? Если мы накопили данные и провели обобщения, то как из множества возможных понятий выбрать те, что лучше всего подходят для описания конкретной ситуации? Что вообще есть обобщения? Как выглядит система соотнесения обобщений между собой?
Далее я попробую дать и «правильную» постановку задачи, и возможный ответ, подкрепленный работающим кодом. Но это будет через статью. Пока же, в следующей части, нам предстоит познакомиться с одной очень важной биологической подсказкой, дающей, пожалуй, главный ключ к пониманию механизма обобщения.