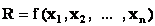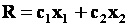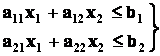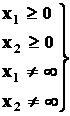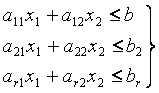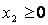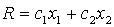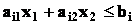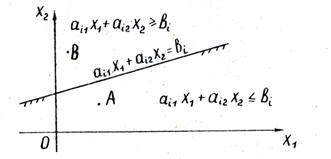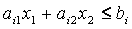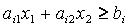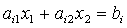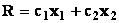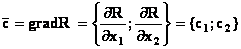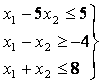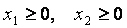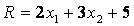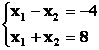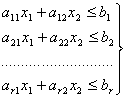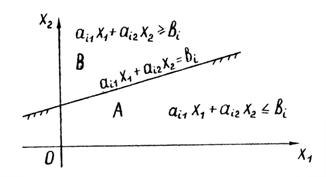что такое область допустимых решений
Область допустимых значений (ОДЗ): теория, примеры, решения
Любое выражение с переменной имеет свою область допустимых значений, где оно существует. ОДЗ необходимо всегда учитывать при решении. При его отсутствии можно получить неверный результат.
В данной статье будет показано, как правильно находить ОДЗ, использовать на примерах. Также будет рассмотрена важность указания ОДЗ при решении.
Допустимые и недопустимые значения переменных
Данное определение связано с допустимыми значениями переменной. При введении определения посмотрим, к какому результату приведет.
Начиная с 7 класса, мы начинаем работать с числами и числовыми выражениями. Начальные определения с переменными переходят к значению выражений с выбранными переменными.
Если имеется выражение с переменными, то оно имеет смысл только тогда, когда при их подстановке значение может быть вычислено.
Если имеется выражение с переменными, то оно не имеет смысл, когда при их подстановке значение не может быть вычислено.
То есть отсюда следует полное определение
Существующими допустимыми переменными называют такие значения, при которых выражение имеет смысл. А если смысла не имеет, значит они считаются недопустимыми.
Для уточнения вышесказанного: если переменных более одной, тогда может быть и пара подходящих значений.
Что такое ОДЗ?
Область допустимых значений – важный элемент при вычислении алгебраических выражений. Поэтому стоит обратить на это внимание при расчетах.
Область ОДЗ – это множество значений, допустимых для данного выражения.
Рассмотрим на примере выражения.
Как найти ОДЗ? Примеры, решения
Найти ОДЗ означает найти все допустимые значения, подходящие для заданной функции или неравенства. При невыполнении этих условий можно получить неверный результат. Для нахождения ОДЗ зачастую необходимо пройти через преобразования в заданном выражении.
Существуют выражения, где их вычисление невозможно:
Все это говорит о том, как важно наличие ОДЗ.
Найти ОДЗ выражения x 3 + 2 · x · y − 4 .
Решение
В куб можно возводить любое число. Данное выражение не имеет дроби, поэтому значения x и у могут быть любыми. То есть ОДЗ – это любое число.
Ответ: x и y – любые значения.
Решение
Видно, что имеется одна дробь, где в знаменателе ноль. Это говорит о том, что при любом значении х мы получим деление на ноль. Значит, можно сделать вывод о том, что это выражение считается неопределенным, то есть не имеет ОДЗ.
Решение
Решение
Почему важно учитывать ОДЗ при проведении преобразований?
При тождественных преобразованиях важно находить ОДЗ. Бывают случаи, когда существование ОДЗ не имеет место. Чтобы понять, имеет ли решение заданное выражение, нужно сравнить ОДЗ переменных исходного выражения и ОДЗ полученного.
Рассмотрим на примере.
Рассмотрим пример с наличием подкоренного выражения.
Нужно избегать преобразований, которые сужают ОДЗ.
Следует придерживаться тождественных преобразований, которые ОДЗ не изменят.
Если имеются примеры, которые его расширяют, тогда его нужно добавлять в ОДЗ.
При наличии логарифмов дело обстоит немного иначе.
При решении всегда необходимо обращать внимание на структуру и вид данного по условию выражения. При правильном нахождении области определения результат будет положительным.
Что такое область допустимых решений
5. Многомерная оптимизация
Оптимизация – это целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.
Количественная оценка оптимизируемого качества называется критерием оптимальности или целевой функцией. Её можно записать в виде:
Существуют два типа задач оптимизации – безусловные и условные.
Безусловная задача оптимизации состоит в отыскании максимума или минимума действительной функции (5.1) от n действительных переменных и определении соответствующих значений аргументов.
Решение задач оптимизации, в которых критерий оптимальности является линейной функцией независимых переменных (то есть содержит эти переменные в первой степени) с линейными ограничениями на них, составляет предмет линейного программирования.
Слово «программирование» отражает здесь конечную цель исследования – определение оптимального плана или оптимальной программы, по которой из множества возможных вариантов исследуемого процесса выбирают по какому-либо признаку наилучший, оптимальный, вариант.
Примером такой задачи является задача оптимального распределения сырья между различными производствами при максимальной стоимости продукции.
Пусть из двух видов сырья изготавливается продукция двух видов.
Учитывая, что расход данного ресурса не может превышать общего его количества, запишем ограничительные условия по ресурсам:
В аналогичном виде формулируются так называемые транспортные задачи (задачи оптимальной организации доставки товаров, сырья или продукции из различных складов к нескольким пунктам назначения при минимуме затрат на перевозку) и ряд других.
Графический метод решения задачи линейного программирования.
и условиям неотрицательности :
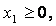
для которых функция
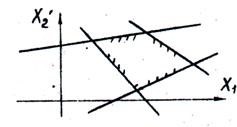
Построим в системе прямоугольных координат x 1 Ox 2 область допустимых решений задачи (рис.11). Для этого, заменяя каждое из неравенств (5.5) равенством, строим соответствующую ему граничную прямую:
а для координат любой точки В другой полуплоскости – противоположное неравенство:
Координаты любой точки граничной прямой удовлетворяют уравнению:
Для определения того, по какую сторону от граничной прямой располагается полуплоскость, соответствующая заданному неравенству, достаточно «испытать» одну какую-либо точку (проще всего точку О (0;0)). Если при подстановке её координат в левую часть неравенства оно удовлетворяется, то полуплоскость обращена в сторону к испытуемой точке, если же неравенство не удовлетворяется, то соответствующая полуплоскость обращена в противоположную сторону. Направление полуплоскости показывается на чертеже штриховкой. Неравенствам:
соответствуют полуплоскости, расположенные справа от оси ординат и над осью абсцисс.
На рисунке строим граничные прямые и полуплоскости, соответствующие всем неравенствам.
Общая, часть (пересечение) всех этих полуплоскостей будет представлять собой область допустимых решений данной задачи.
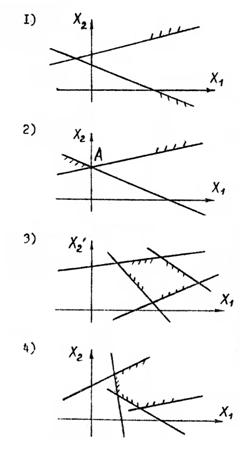
При построении области допустимых решений в зависимости от конкретного вида системы ограничений (неравенств) на переменные может встретиться один из следующих четырех случаев:
Рис. 12. Область допустимых решений пустая, что соответствует несовместности системы неравенств; решения нет
Рис. 14. Область допустимых решений ограниченная, изображается в виде выпуклого многоугольника. Допустимых решений бесконечное множество
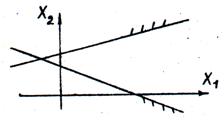
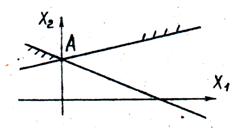
Рис. 15. Область допустимых решений неограниченная, в виде выпуклой многоугольной области. Допустимых решений бесконечное множество
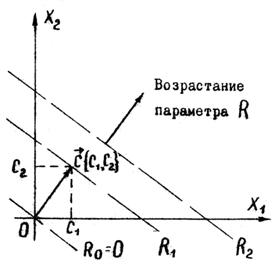
Графическое изображение целевой функции
Задача отыскания оптимального решения системы неравенств (5.5), для которого целевая функция R (5.7) достигает максимума, геометрически сводится к определению в области допустимых решений точки, через которую пройдет линия уровня, соответствующая наибольшему значении параметра R
Если область допустимых решений есть выпуклый многоугольник, то экстремум функции R достигается, по крайней мере, в одной из вершин этого многоугольника.
Если экстремальное значение R достигается в двух вершинах, то такое же экстремальное значение достигается в любой точке на отрезке, соединяющем эти две вершины. В этом случае говорят, что задача имеет альтернативный оптимум.
В случае неограниченной области экстремум функции R либо не существует, либо достигается в одной из вершин области, либо имеет альтернативный оптимум.
и условиям неотрицательности :
для которых функция:
Заменим каждое из неравенств равенством и построим граничные прямые:
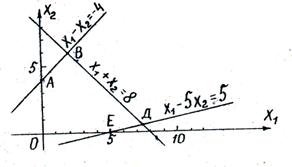
Определим полуплоскости, соответствующие данным неравенствам, путём «испытания» точки (0;0). С учетом неотрицательности x 1 и x 2 получим область допустимых решений данной задачи в виде выпуклого многоугольника ОАВДЕ.
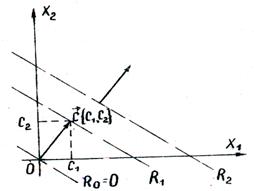
В области допустимых решений находим оптимальное решение, строя вектор градиента
Задания. Найти положение точки экстремума и экстремальное значение целевой функции
Сервис для решения задач по линейному программированию
при следующих ограничениях:
 | 3 x1 | + | 5 x2 | ≤ | 30 |
| 4 x1 | — | 3 x2 | ≤ | 12 | |
| x1 | — | 3 x2 | ≥ | 6 |
x1 ≥ 0 x2 ≥ 0
Точки, координаты которых удовлетворяют одновременно всем неравенствам системы ограничений, называются областью допустимых решений.
Это стандартная схема решения. Если область допустимых решений представляет собой точку или пустое множество, то решение будет короче.
По условию задачи: x1 ≥ 0 x2 ≥ 0.
Если бы это было единственным условием, то область допустимых решений имела бы вид, как на рисунке (вся первая четверть).
Рассмотрим неравенство 1 системы ограничений.
Построим прямую: 3 x1 + 5 x2 = 30
Преобразуем неравенство, оставив в левой части только x2
Объединим данное условие с предыдущим рисунком. В итоге получим область допустимых решений, изображенную на рисунке.
Рассмотрим неравенство 2 системы ограничений.
Преобразуем неравенство, оставив в левой части только x2
Объединим данное условие с предыдущим рисунком. В итоге получим область допустимых решений, изображенную на рисунке.
Рассмотрим неравенство 3 системы ограничений.
Преобразуем неравенство, оставив в левой части только x2
Из рисунка видно, что данная область не имеет общих точек с областью допустимых решений, полученной на предыдущем шаге.
Что такое область допустимых решений
4.2. Графический метод решения задач линейного программирования
Найти X 1 и X 2 удовлетворяющие системе неравенств:
для которых функция:
Построим в системе прямоугольных координат Х1ОХ2 область допустимых решений задачи. Для этого, заменяя каждое из неравенств (37) равенством, строим соответствующую ему граничную прямую ai 1 x 1 + ai 2 x 2 ≤ bi ( i =1,2,…, r ) (рис.17).
Координаты любой точки граничной прямой удовлетворяют уравнению:
Для определения, по какую сторону от граничной прямой располагается полуплоскость, соответствующая заданному неравенству, достаточно «испытать» одну какую-либо точку (проще всего точку О (0,0 ) ). Если при подстановке ее координат в левую часть неравенства оно удовлетворяется, то полуплоскость обращена в сторону к испытуемой точке, если же неравенство не удовлетворяется, то соответствующая полуплоскость обращена в противоположную сторону. Направление полуплоскости показывается на чертеже (рис.17) штриховкой.
Неравенствам X 1 ≥0 и X 2 ≥0 также соответствуют полуплоскости, расположенные справа от оси ординат и над осью абсцисс.
На рисунке строим граничные прямые и полуплоскости, соответствующие всем неравенствам.
Общая часть (пересечение) всех этих полуплоскостей будет представлять собой область допустимых решений данной задачи.
При построении области допустимых решений в зависимости от конкретного вида системы ограничений (неравенств) на переменные может встретиться один из четырех случаев (рис.18):
Область допустимых решений пустая, что соответствует несовместности системы неравенств; решения нет.
Область допустимых решений ограниченная, изображается в виде выпуклого многоугольника. Допустимых решений множество.
Область допустимых решений неограниченная, в виде выпуклой многоугольной области. Допустимых решений множество.
Для всех точек, лежащих на одной из прямых, функция R принимает одно определенное значение, поэтому указанные прямые называются линиями уровня для функции R (рис.19).
Если область допустимых решений есть выпуклый многоугольник» то экстремум функции R достигается по крайней мере в одной из вершин этого многоугольника.
Если экстремальное значение R достигается в двух вершинах, то же экстремальное значение достигается в любой точке на отрезке, соединяющем эти две вершины. В этом случае говорят, что задача имеет альтернативный оптимум.
В случае неограниченной области экстремум функции R либо не существует, либо достигается в одной из вершин области, либо имеет альтернативный оптимум.
59. Опорное решение задачи линейного программирования, его взаимосвязь с угловыми точками
Каноническая задача линейного программирования в векторной форме имеет вид:
Положительным координатам допустимых решений ставятся в соответствие векторы условий. Эти системы векторов зависимы, так как число входящих в них векторов больше размерности векторов.
Базисным решением системы называется частное решение, в котором неосновные переменные имеют нулевые значения. Любая система уравнений имеет конечное число базисных решений, равное 
, где 
– число неизвестных, 
– ранг системы векторов условий. Базисные решения, координаты которых удовлетворяют условию неотрицательности, являются опорными.
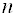
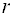
Опорным решением задачи линейного программирования называется такое допустимое решение 
, для которого векторы условий, соответствующие положительным координатам 
, линейно независимы.
Число отличных от нуля координат опорного решения не может превосходить ранга 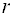Системы векторов условий (т. е. числа линейно независимых уравнений системы ограничений).
Если число отличных от нуля координат опорного решения равно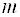 
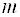
, то такое решение называется Невырожденным, в противном случае, если число отличных от нуля координат опорного решения меньше , такое решение называется Вырожденным.
Базисом опорного решения называется базис системы векторов условий задачи, в состав которой входят векторы, соответствующие отличным от нуля координатам опорного решения.
Теорема. Любое опорное решение является угловой точкой области допустимых решений.
Теорема. Любая угловая точка области допустимых решений является опорным решением.
Графический метод решения задачи линейной оптимизации рассмотрим на примере задачи производственного планирования при
= 2.
Предприятие изготавливает изделия двух видов А и В. Для производства изделий оно располагает сырьевыми ресурсами трех видов С, D и Е в объемах 600, 480 и 240 единиц соответственно. Нормы расхода ресурсов на единицу продукции каждого вида известны и представлены в табл. 14.1
Построим математическую модель задачи, для чего обозначим 
и 
— объемы производства изделий А и В соответственно.
Тогда прибыль предприятия от реализации изделий А и изделий В составит:
.
Ограничения по ресурсам будут иметь вид:
Естественно, объемы производства должны быть неотрицательными 
.
Решение сформулированной задачи найдем, используя геометрическую интерпретацию. Определим сначала многоугольник решений, для чего систему ограничений неравенств запишем в виде уравнений и пронумеруем их:
Каждое из записанных уравнений представляет собой прямую на плоскости, причем 4-я и 5-я прямые являются координатными осями.
Чтобы построить первую прямую, найдем точки ее пересечения с осями координат: при 
, а при 
. Далее нас интересует, по какую сторону от прямой будет находиться полуплоскость, соответствующая первому неравенству. Чтобы определить искомую полуплоскость, возьмем точку 
и, подставив ее координаты в неравенство, видим, что оно удовлетворяется. Так как точка 
лежит левее первой прямой, то и полуплоскость будет находиться левее прямой 
. На рис. 14.1 расположение полуплоскости относительно первой прямой отмечено стрелками.
Аналогично построены 2-я и 3-я прямые и найдены полуплоскости, соответствующие 2-му и 3-му неравенству. Точки, удовлетворяющие ограничениям 
, находятся в первом квадранте.
Множество точек, удовлетворяющих всем ограничениям одновременно, является ОДР системы ограничений. Такой областью на графике (рис. 14.1) является многоугольник 
.
Любая точка многоугольника решений удовлетворяет системе ограничений задачи и, следовательно, является ее решением. Это говорит о том, что эта задача линейной оптимизации имеет множество допустимых решений, т. е. многовариантна. Нам же необходимо найти решение, обеспечивающее максимальную прибыль.
Чтобы найти эту точку, приравняем функцию к нулю и построим соответствующую ей прямую. Вектор–градиент прямой функции 
имеет координаты 
.
 |
Рис. 14.1
Изобразим вектор на графике и построим прямую функции перпендикулярно вектору на рис. 14.1. Перемещая прямую функции параллельно самой себе в направлении вектора, видим, что последней точкой многоугольника решений, которую пересечет прямая функции, является угловая точка В. Следовательно, в точке В функция достигает максимального значения. Координаты точки В находим, решая систему уравнений, прямые которых пересекаются в данной точке.
Решив эту систему, получаем, что 
.
Следовательно, если предприятие изготовит изделия в найденных объемах, то получит максимальную прибыль, равную:
(млн. руб.).
Алгоритм решения задачи линейного программирования графическим методом таков:
1. Строится область допустимых решений;
2. Строится вектор нормали к линии уровня с точкой приложении в начале координат;
3. Перпендикулярно вектору нормали проводится одна из линий уровня, проходящая через начало координат;
4. Линия уровня перемещается до положения опорной прямой. На этой прямой и будут находиться максимум или минимум функции.
В зависимости от вида области допустимых решений и целевой функции задача может иметь единственное решение, бесконечное множество решений или не иметь ни одного оптимального решения.
На рис. 14.3 показан случай, когда прямая функции параллельна отрезку АВ, принадлежащему ОДР. Максимум функции 
достигается в точке А и в точке В, а, следовательно, и в любой точке отрезка АВ, т. к. эти точки могут быть выражены в виде линейной комбинации угловых точек А и В.
Основные понятия симплексного метода решения задачи линейного программирования.
Среди универсальных методов решения задач линейного программирования наиболее распространен симплексный метод (или симплекс-метод), разработанный американским ученым Дж. Данцигом. Суть этого метода заключается в том, что вначале получают допустимый вариант, удовлетворяющий всем ограничениям, но необязательно оптимальный (так называемое начальное опорное решение); оптимальность достигается последовательным улучшением исходного варианта за определенное число этапов (итераций). Нахождение начального опорного решения и переход к следующему опорному решению проводятся на основе применения рассмотренного выше метода Жордана-Гаусса для системы линейных уравнений в канонической форме, в которой должна быть предварительно записана исходная задача линейного программирования; направление перехода от одного опорного решения к другому выбирается при этом на основе критерия оптимальности (целевой функции) исходной задачи.
Симплекс-метод основан на следующих свойствах задачи линейного программирования:
· Не существует локального экстремума, отличного от глобального. Другими словами, если экстремум есть, то он единственный.
· Множество всех планов задачи линейного программирования выпукло.
· Целевая функция ЗЛП достигает своего максимального (минимального) значения в угловой точке многогранника решений (в его вершине). Если целевая функция принимает свое оптимальное значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.
· Каждой угловой точке многогранника решений отвечает опорный план ЗЛП.
Рассмотрим две разновидности симплексного метода: симплекс-метод с естественным базисом и симплекс-метод с искусственным базисом (или М-метод).
Симплекс-метод с естественным базисом
Для применения этого метода задача линейного программирования должна быть сформулирована в канонической форме, причем матрица системы уравнений должна содержать единичную подматрицу размерностью 
. В этом случае очевиден начальный опорный план (неотрицательное базисное решение).
Для определенности предположим, что первые Т Векторов матрицы системы составляют единичную матрицу. Тогда очевиден первоначальный опорный план: 
.
Проверка на оптимальность опорного плана проходит с помощью критерия оптимальности, переход к другому опорному плану — с помощью преобразований Жордана-Гаусса и с использованием критерия оптимальности.
Полученный опорный план снова проверяется на оптимальность и т. д. Процесс заканчивается за конечное число шагов, причем на последнем шаге либо выявляется неразрешимость задачи (конечного оптимума нет), либо получаются оптимальный опорный план и соответствующее ему оптимальное значение целевой функции.
Признак оптимальности заключается в следующих двух теоремах.
Теорема 1. Если для некоторого вектора, не входящего в базис, выполняется условие:
, где 
, 
То можно получить новый опорный план, для которого значение целевой функции будет больше исходного; при этом могут быть два случая:
1. Если все координаты вектора, подлежащего вводу в базис, неположительны, то задача линейного программирования не имеет решения;
2. Если имеется хотя бы одна положительная координата у вектора, подлежащего вводу в базис, то можно получить новый опорный план.
Теорема 2. Если для всех векторов выполняется условие 
, то полученный план является оптимальным.
На основании признака оптимальности в базис вводится вектор 
, давший минимальную отрицательную величину симплекс-разности: 
.
Чтобы выполнялось условие неотрицательности значений опорного плана, выводится из базиса вектор 
Г, Который дает минимальное положительное отношение:
; 
, 
.
Строка Называется Направляющей, Столбец 
и элемент 
— Направляющими (последний называют также Разрешающим Элементом).
Элементы вводимой строки, соответствующей направляющей строке, в новой симплекс-таблице вычисляются по формулам:
,
А элементы любой другой 
-й Строки пересчитываются по формулам:
,,
Значения базисных переменных нового опорного плана (показатели графы «план») рассчитываются по формулам:
для 
; 
, для 
.
Если наименьшее значение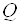 
достигается для нескольких базисных векторов, то чтобы исключить возможность зацикливания (повторения базиса), можно применить следующий способ.
Вычисляются частные, полученные от деления всех элементов строк, давших одинаковое минимальное значение 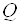на свои направляющие элементы. Полученные частные сопоставляются по столбцам слева направо, при этом учитываются и нулевые, и отрицательные значения. В процессе просмотра отбрасываются строки, в которых имеются большие отношения, и из базиса выводится вектор, соответствующий строке, в которой раньше обнаружится меньшее частное.
Для использования приведенной выше процедуры симплекс-метода к минимизации линейной формы 
следует искать максимум функции 
, затем полученный максимум взять с противоположным знаком. Это и будет искомый минимум исходной задачи линейного программирования.
Симплексный метод с искусственным базисом (М-метод)
Симплексный метод с искусственным базисом применяется в тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи линейного программирования, записанной в канонической форме.
М-метод заключается в применении правил симплекс-метода к так называемой М-задаче. Она получается из исходной добавлением к левой части системы уравнений в канонической форме исходной задачи линейного программирования таких искусственных единичных векторов с соответствующими неотрицательными искусственными переменными, чтобы вновь полученная матрица содержала систему единичных линейно-независимых векторов. В линейную форму исходной задачи добавляется в случае её максимизации слагаемое, представляющее собой произведение числа (–М) на сумму искусственных переменных, где М – достаточно большое положительное число.
В полученной задаче первоначальный опорный план очевиден. При применении к этой задаче симплекс-метода оценки 
теперь будут зависеть от числа М. Для сравнения оценок нужно помнить, что М – достаточно большое положительное число, поэтому из базиса будут выводиться в первую очередь искусственные переменные.
В процессе решения М–Задачи следует вычеркивать в симплекс-таблице искусственные векторы по мере их выхода из базиса. Если все искусственные векторы вышли из базиса, то получаем исходную задачу. Если оптимальное решение М–Задачи содержит искусственные векторы или М–Задача неразрешима, то исходная задача также неразрешима.
Путем преобразований число вводимых переменных, составляющих искусственный базис, может быть уменьшено до одной.