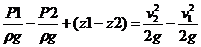что такое объемный расход жидкости
Измерение расхода жидкости: приборы и методы
Расход – это объем жидкости протекающий в единицу времени через поперечное сечение трубопровода. Измерение расхода жидкости является одной из задач при производственных испытаниях оборудования.
В этой статье мы собрали для Вас все современные методы определения расхода жидкости, а так же приборы для измерения расхода: трубчатые расходомеры, расходомерные шайбы, крыльчатые расходомеры, ультразвуковые и вихревые расходомеры.
Содержание статьи
Методы измерения расхода жидкости
Наиболее простые и вместе с тем точные методы измерения расхода жидкости являются объемный и массовый (весовой).
В соответствии с методами измерения, единицами расхода жидкости являются:


При объемном способе измерения протекающая в исследуемом потоке(например, в трубе) жидкость поступает в особый, тщательно протарированный сосуд (так называемый мерник), время наполнения которого точно фиксируется по секундомеру.
Если известен объем мерника – V и измеренное время его наполнения – T, то объемный расход будет
При весовом способе взвешиванием находят вес Gv = mv*g (где g – ускорение свободного падения) всей жидкости, поступившей в мерник за время T. Затем определяют её массу
и по ней, зная плотность жидкости (ρ), вычисляют объемный расход
Но объемный и весовой методы измерения расхода жидкости пригодны только при сравнительно небольших значениях расхода жидкости, так как в противном случае размеры мерников получаются довольно громоздкими и, как следствие, замеры очень затруднительными.
Кроме того, этими способами невозможно измерить расход в произвольном сечении, например, длинного трубопровода или канала без нарушения их целостности. Поэтому, за исключением случаев измерения сравнительно небольших расходов жидкостей в коротких трубах и каналах, объемный и весовой способы, как правило, не применяются, а на практике пользуются специальными приборами, которые предварительно тарируются объемным или весовым способом.
Приборы для измерения расхода жидкости
Трубчатые расходомеры
Одним из таких приборов является трубчатый расходомер или расходомер Вентури. Большим достоинством этого расходомера является простота конструкции и отсутствие в нем каких-либо движущихся частей. Трубчатые расходомеры могут быть горизонтальными и вертикальными. Рассмотрим, к примеру, горизонтальный вариант.
Расходомер состоит из двух цилиндрических труб А и В диаметра d1, соединенных при помощи двух конических участков (патрубков) С и D с цилиндрической вставкой E меньшего диаметра d2. В сечениях 1-1 и 2-2 расходомера присоединены пьезометрические трубки a и b, разность уровней жидкости h в которых показывает разность давлений в этих сечениях.
Расход жидкости в этом случае определяется по тарировочным кривым, полученным опытным путем и дающим для данного расходомера прямую зависимость между показаниями манометра и измеряемыми расходами жидкости. Пример такой кривой на картинке рядом
Расходомерная шайба
Другим широко распространенным прибором для измерения расхода является расходомерная шайба (или диафрагма), обычно выполняемая в виде плоского кольца с круглым отверстием в центре, устанавливаемого между фланцами трубопровода
Края отверстия чаще всего имеют острые входные кромки под углом 45° или закругляются по форме втекающей в отверстие струи жидкости (сопло). Два пьезометра a и b (или дифференциальный манометр) служат для измерения перепада давления до и после диафрагмы. В основе метода положен принцип неразрывности Бернулли.
Расход в этом случае определяется по замеренной разности уровней в трубках. Трубки подсоединяют к датчикам, замеряющим перепад давления. Датчик перепада давления преобразует перепад в электрический сигнал, который отправляется на компьютер.
Крыльчатый расходомер
Расходы могут быть вычислены также в результате измерения скоростей течения жидкости и живых течений потока.
Одним из широко распространенных приборов, применяемых для этой цели является гидрометрическая вертушка. Современный турбинный расходомер устанавливают только на горизонтальном участке трубопровода. Лопасти крыльчатки колеса турбины изготавливают из не магнитного материала.
Вертушка состоит из крыльчатки А, представляющей собой колесо с винтовыми лопастями, насаженное на горизонтальный вал С. Когда она установлена в потоке, крыльчатка под действием протекающей жидкости вращается, причем число её оборотов прямо пропорционально скорости течения. Число импульсов за один оборот крыльчатки равно числу лопастей, а значит частота импульсов пропорциональна расходу.
При вращении лопасти поочередно пересекают магнитное поле, которое наводит электродвижущую силу в катушке в виде импульса. От вертушки вверх выводятся провода В, подающему сигнал к специальному счетчику, автоматически записывающему число оборотов и время.
Приборы для измерения расхода жидкости в этом случае называют турбинными расходомерами
Ультразвуковой метод измерения расхода
Ультразвуковой расходомер работает по принципу использования разницы по времени прохождения ультразвукового сигнала в направлении потока и против него.
Расходомер формирует электрический импульс, поступающий на пьезоэлемент П1, который излучает электромеханические колебания в движущуюся среду. Эти колебания воспринимаются через некоторое время пьезоэлементом П2, преобразуются им в электрический импульс, попадающий в электронное устройство и снова направляемый им на пьезоэлемент П1 и т.д.
Такой контур П1-П2 характеризуется частотой f1 повторений импульсов, прямо пропорциональной расстоянию между пьезоэлементами и обратно пропорциональной разности между скоростью распространения звука в контролируемой среде и скоростью самой среды.
Аналогично электронное устройство подает импульсы в обратном направлении, т.е. от пьезоэлемента П2 к пьезоэлементу П1. Контур П2-П1 характеризуется своей частотой f2 повторений импульсов, прямо пропорциональной расстоянию между пьезоэлементами и обратно пропорциональной сумме скоростей распространения звука в среде и самой среды.
Следующим шагом является определение разности Δf указанных частот, которая пропорциональна расходу среды. Приборы для измерения расхода жидкости называются ультразвуковые расходомеры.
Вихревой метод измерения расхода
В основу работы вихревых расходомеров положена зависимость между расходом и частотой возникновения вихрей за твердым телом (например, металлическим прямоугольным стержнем), которое расположено в потоке жидкости или газа.
Принцип действия преобразователя основан на ультразвуковом детектировании вихрей, образующихся в потоке жидкости, при обтекании жидкостью специальной призмы, расположенной поперек потока.
В зависимости от конструкции датчика чувствительные тепловые элементы устанавливаются непосредственно в теле датчика или вихревой дорожке.
Если в тело образующее вихри, установить магнит, то он может служить датчиком. Реакция, возникающая при срыве вихрей, заставляет помещённый в поток цилиндр колебаться с частотой вихреобразования. Достоинством вихревых расходомеров является, обеспечение низкой зависимости качества измерений от физико-химических свойств жидкости, состояния трубопровода, распределения скоростей по сечению потока и от точности монтажа первичных преобразователей на трубопроводе. Приборы для измерения расхода жидкости называются вихревые расходомеры.
Видео о измерении расхода
При проведении измерения расхода, в некоторых случая используется понятие количества вещества – это количество жидкости или другой среды, проходящей через поперечное сечение трубопровода в течении определенного промежутка времени(за час, месяц, рабочую смену и т.д.)
Приборы для измерения количества вещества по аналогии с измерением расхода монтируются на – на трубопроводе, с выводом вторичного прибора к оператору.
Что такое объемный расход жидкости
5-я лекция, 2010 год.
5. КИНЕМАТИКА И ДИНАМИКА ЖИДКОСТИ
5.1. Основные понятия
5.2. Расход. Уравнение расхода
5.3. Уравнение Бернулли для элементарной струйки идеальной жидкости.
Три вида уравнения Бернулли для струйки идеальной жидкости.
5.1. Основные понятия
Кинематика жидкости существенно отличается от кинематики твердого тела. Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жидкой среде такие связи отсутствуют; жидкость состоит из множества частиц движущихся одна относительно другой.
Скорость в данной точке пространства, занятого движущейся жидкостью, является функцией координат этой точки, а иногда и времени.
Задачей кинематики жидкости является определение скорости в любой точке жидкой среды, т. е. нахождение поля скоростей.
Мы сейчас рассмотрим движение идеальной жидкости, то есть жидкости, которая не обладает вязкостью.
В идеальной жидкости, так же как и в неподвижной реальной жидкости, возможен лишь один вид напряжений — нормальные напряжения сжатия, т. е. гидромеханическое давление.
Давление в движущейся идеальной жидкости обладает теми же свойствами, что и в неподвижной жидкости, на внешней поверхности жидкости оно направлено по нормали, а в любой точке внутри жидкости по всем направлениям одинаково.
Течение жидкости может быть установившимся или неустановившимся.
Установившимся называется течение жидкости, при котором давление и скорость являются функциями координат и не зависят от времени.
Давление и скорость могут измениться при перемещении частицы жидкости из одного положения в другое, но в данной неподвижной относительно русла точке давление и скорость при установившемся движении не изменяются во времени.
Последнее положение доказывается подобно тому, как это делалось для неподвижной жидкости (см. п. 1.4): составляются уравнения движения элементарного тетраэдра с учетом сил Д’Аламбера, которые затем вместе с массовыми силами стремятся к нулю при стягивании тетраэдра в точку.
где индексы у скорости означают ее проекции на соответствующие оси, жестко связанные с руслом.
Примером установившегося течения может служить истечение жидкости из со суда, в котором поддерживается постоянный уровень, или движение жидкости в трубопроводе, создаваемое центробежным насосом с постоянной частотой вращения вала.
Неустановившимся называется течение жидкости, характеристики которого изменяются во времени в точках рассматриваемого пространства.
В общем случае при неустановившемся течении давление и скорость зависят как от координат, так и от времени:
Примерами неустановившегося течения жидкости могут служить быстрое опорожнение сосуда через отверстие в дне или движение во всасывающей или напорной трубе поршневого насоса, поршень которого совершает возвратно-поступательное движение.
Исследование установившихся течений гораздо проще, чем неустановившихся.
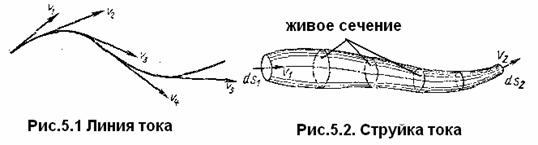
При установившемся течении траектории частиц жидкости являются неизменными по времени. При неустановившемся течении траектории различных частиц, проходящих через данную точку пространства, могут иметь разную форму. Поэтому для рассмотрения картины течения, возникающей в каждый данный момент времени, вводится понятие линии тока.
Линией тока называется кривая, в каждой точке которой вектор скорости в данный момент времени направлен по касательной к этой кривой (рис. 5.1).
Очевидно, что в условиях установившегося течения линия тока совпадает с траекторией частицы и не изменяет своей формы с течением времени.
Трубкой тока называется бесконечно малый замкнутый контур, выделенный в данный момент времени в движущейся жидкости, через все точки которого проведены линии тока. Это условная трубчатая поверхность.
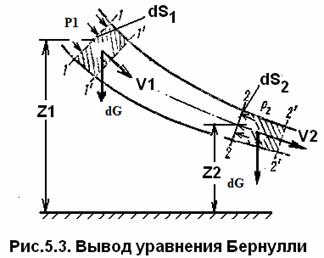
Элементарной струйкой называется часть потока, заключенная внутри трубки тока (рис.5.2).
В любой точке «трубки тока» т.е. на трубчатой поверхности струйки, векторы скорости направлены по касательной, а нормальные к этой поверхности составляющие скорости отсутствуют, следовательно, при установившемся движении ни одна частица жидкости, ни в одной точке трубки тока не может проникнуть внутрь струйки или выйти наружу.
Трубка тока, таким образом, является как бы непроницаемой стенкой, а элементарная струйка представляет собой самостоятельный элементарный поток.
Потоки конечных размеров будем сначала рассматривать, как совокупность элементарных струек, т. е. будем предполагать течение струйным. Из-за различия скоростей соседние струйки будут скользить одна по другой, но не будут перемешиваться одна с другой.
Живым сечением или сечением потока, называется площадь поверхности в пределах потока или струйки, проведенная нормально к линиям тока. Далее будем рассматривать в потоках такие участки, в которых струйки можно считать параллельными и, следовательно, живые сечения плоскими.
Различают напорные и безнапорные течения жидкости. Напорными называют течения в закрытых руслах без свободной поверхности, а безанапорными течения со свободной поверхностью. При напорных течениях давление вдоль потока обычно переменное, при безнапорном на свободной поверхности постоянное и чаще всего атмосферное. Примерами напорного течения могут служить течения в трубопроводах с повышенным (или пониженным) давлением, в гидромашинах или других гидроагрегатах. Безнапорными являются течения в реках, открытых каналах и лотках.
5.2. Расход. Уравнение расхода
Для элементарной струйки, имеющей бесконечно малые площади сечений, можно считать истинную скорость одинаковой во всех точках каждого сечения. Следовательно, для этой струйки расходы равны.
где dS – площадь сечения струйки.
Для потока конечных размеров в общем случае скорость имеет различное значение в разных точках сечения, поэтому расход надо определять, как сумму элементарных расходов струек в данном сечении.
Обычно в рассмотрение вводят среднюю по сечению скорость v ср = Q / S , откуда средний расход для струйки или потока равен
Условие неразрывности потока основывается на следующих свойствах, законе и предпосылках.
а) трубка тока имеет свойство непроницаемости для внешних, обтекающих ее потоков;
б) закон сохранения вещества;
в) предположение о сплошности (неразрывности) среды для установившегося течения несжимаемой жидкости.
На основании этих предпосылок и свойств можно утверждать, что объемный расход во всех сечениях элементарной струйки (см. рис.5.2) один и тот же
dQ = v 1 * dS 1 = v 2 * dS 2 → const (вдоль струйки). (5.6)
Это уравнение называется уравнением объемного расхода для элементарной струйки.
Аналогичное уравнение можно составить и для потока конечных размеров, ограниченного непроницаемыми стенками, только вместо истинных скоростей следует ввести средние скорости. В результате
Из последнего уравнения следует, что средние скорости в потоке несжимаемой жидкости обратно пропорциональны площадям сечений:
У равнение расхода (5.6‘) является следствием общего закона сохранения вещества для частных условий, в частности? для условий сплошности (неразрывности) течения.
5.3. Уравнение Бернулли для элементарной струйки
Рассмотрим установившееся течение идеальной жидкости находящейся под действием одной массовой силы — силы тяжести, и выведем для этого случая основное уравнение, связывающее между собой давление в жидкости и скорость ее движения.
Применим к массе жидкости в объеме участка струйки теорему о кинетической энергии: работа сил, приложенных к телу, равна приращению кинетической энергии этого тела.
На жидкость действуют силы тяжести и силы давления, нормально к поверхности сечения рассматриваемого участка струйки.
Работа силы давления в первом сечении положительна, так как направление силы совпадает с направлением перемещения, и выражается как произведение силы p 1* dS на путь V 1 dt :
Работа силы давления во втором сечении имеет знак минус, так как направление силы прямо противоположно направлению перемещения, и определяется выражением
Силы давления, действующие по боковой поверхности отрезка струйки, работы не производят, так как они нормальны к этой поверхности и к перемещениям.
Работа сил давления равна
Тогда работа силы тяжести выразится как произведение разности высот на силу тяжести dG :
Таким образом, приращение кинетической энергии на участке струйки равно
Сложив работу сил давления (см. уравнение 5.7) с работой силы тяжести (5.9) и приравняв эту сумму приращению кинетической энергии (5.10), получим исходное уравнение для трех видов уравнения Бернулли.
Сгруппируем члены, относящиеся к первому сечению, в левой части уравнения, а члены, относящиеся ко второму сечению, в правой:
где z — геометрическая высота, или геометрический напор;
Р/ρ g – пьезометрическая высота или пьезометрический напор;
v 2 /2 g — скоростная высота или скоростной напор.
Это уравнение является первой формой уравнения Бернулли, оно
называется полным напором и имеет размерность длины.
Данное уравнение получено путем деления исходного уравнения (5.11), выражающего теорему об изменении кинетической энергии элементарной струйки, на ее изменении ее силы тяжести за время dt .
Уравнение Бернулли (5.13) записано для двух произвольно взятых сечении струйки и выражает равенство полных напоров Н в этих сечениях. Так как сечения взяты произвольно, следовательно, и для любого другого сечения этой же струйки полный напор будет иметь то же значение
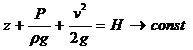
Для идеальной движущейся жидкости вдоль струйки тока сумма трех напоров: геометрического, пьезометрического и скоростного есть величина постоянная.
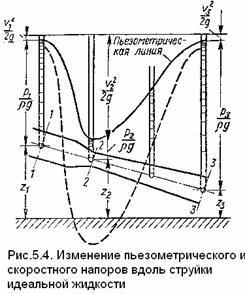
На рис. 5.4 показано изменение всех напоров вдоль струйки.
Линия изменения уровней жидкости в пьезометрах называется пьезометрической линией.
Из уравнения Бернулли и уравнения расхода следует, что если площадь поперечного сечения струйки уменьшается, т. е. струйка сужается, то скорость течения жидкости увеличивается, а давление уменьшается, и наоборот, если струйка расширяется, то скорость уменьшается, а давление возрастает.
Штриховой линией показано положение пьезометрической линия при тех же сечениях и при увеличении расхода в 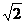
Уравнение Бернулли можно записать в двух других формах. Разделив уравнение (5.11) на расход dQ = dS 1* v 1 dt = dS 2* v 2 dt , учитывая, что dG = ρ *g*dQ, а dQ = dG / ρ g, получим
где все величины выражены в виде давлений.
В этой форме члены уравнения Бернулли имеют размерность давления и имеют следующие называния: ρ zg — весовое давление; р — гидромеханическое давление; ρ v 2 /2 — динамическое давление.
Разделив уравнение (5.11) на массу dm элементарного объема, равную ( ρ * v 1* dS 1) * dt = ( ρ * v 2* dS 2) * dt и преобразуем это уравнение подобно предыдущему. Тогда вместо выражения (5.15) будем иметь
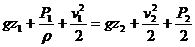
Введем понятие удельной энергии жидкости, в качестве которой рассмотрим отношение энергии к массе или объему.
Нетрудно показать, что члены уравнения (5.16) представляют собой различные формами удельной механической энергии, а именно:
gz — удельная потенциальная энергия (ее еще называют энергией положения), так как частица жидкости массой Δ m , находясь на высоте z , обладает энергией равной Δ mgz , а на единицу массы приходится энергия g Δ mz /Δ m = gz ;
сумма gz + р/ρ – удельная потенциальная энергия жидкости;
Hg = zg + p /ρ+ v 2 /2 – полная удельная механическая энергия движущейся жидкости.
Таким образом, энергетический смысл уравнения Бернулли для элементарной струйки идеальной жидкости заключается в постоянстве вдоль струйки полной удельной энергии жидкости.
Механическая энергия жидкости может иметь три формы: потенциальная энергия, энергия давленияи и кинетическая энергия.
Первая и третья формы механической энергии известны из механики, они свойственны твердым и жидким телам.
Энергия давления является специфической для движущихся жидкостей. В процессе движения идеальной жидкости одна форма энергии может превращаться в другую, однако полная удельная энергия идеальной жидкости при этом как следует из уравнения Бернулли, остается без изменений.
Энергию давления легко преобразовать в механическую работу. Простейшим устройством, с помощью которого осуществляют такое преобразование, является цилиндр с поршнем (рис. 5.5). Покажем, что при этом преобразовании каждая единица массы жидкости совершает работу, численно равную р/ρ.
Объемный, массовый и весовой расходы
Массовый расход — жидкость
Калориметрические расходомеры служат для измерения массового расхода жидкости и газа. Действие их основано на зависимости перепада температуры от подведенного количества теплоты и средней скорости потока измеряемой среды.
С есть умноженный на v R массовый расход жидкости сквозь поверхность пластины, отнесенный к расходу невозмущенного набегающего потока сквозь сечение, равное по величине площади пластины.
Согласно уравнению ( 11 44), массовый расход жидкости через началь — ное сечение трубопровода равен ее расходу через конечное сечение трубопровода. Таким образом, уравнение постоянства расхода является частным случаем закона сохранения массы и выражает материальный баланс потока.
Согласно уравнению ( 11 44), массовый расход жидкости через начальное сечение трубопровода равен ее расходу через конечное сечение трубопровода. Таким образом, уравнение постоянства расхода является частным случаем закона сохранения массы и выражает материальный баланс потока.
Согласно уравнению ( 11 44), массовый расход жидкости через начальное сечение трубопровода равен ее расходу через конечное сечение трубопровода.
| Индикаторная кривая мость. |
В формуле ( 308) q — массовый расход жидкости ; первый член правой части равенства учитывает вязкостные потери давления, второй член — инерционные; левая часть равенства учитывает силы деформации.
| К выводу уравнения постоянства расхода. |
Согласно уравнению ( 11 44), массовый расход жидкости через начальное сечение трубопровода равен ее расходу через конечное сечение трубопровода. Таким образом, уравнение постоянства расхода является частным случаем закона сохранения массы и выражает материальный баланс потока.
Отношение L / П Г, представляющее собой массовый расход жидкости на единицу смоченного периметра, называется линейной плотностью орошения.
Постоянный расход — жидкость
Постоянный расход жидкости в измерительной трубке поддерживается мембранно-пружинным регулятором с. После регулятора жидкость может быть возвращена в систему. Регулятор расхода представляет собой сосуд, разделенный мембраной на две камеры. В нижней камере мембрана поддерживается пружиной, а в верхней камере находится конусный клапан, который закрывает или открывает выходное отверстие. В мембране имеется отверстие, с помощью которого соединяются обе камеры. В равновесном состоянии разность давлений в камерах постоянна и определяется натяжением пружины.
| Зависимость потери напоров при движении газированной жидкости от объема газа. 1 — ha ( m hCK. 2 — h. 3 — / z hCK h. |
При постоянном расходе жидкости ( см. рис. 59) сумма потерь AJJOJ, hCK тем меньше, чем больше газа проходит через трубу данного диаметра. А потери напора на трение с увеличением объема пропускаемого газа увеличиваются. Из рис. 59 видно, что при постоянном расходе жидкости и постоянном диаметре труб потери напора h будут значительно меньше при расходе газа 25 л / с. Увеличение объема подачи газа увеличивает общие потери давления в подъемных трубах при движении в них газожидкостной смеси.
При постоянном расходе жидкости ( г) жп const) изменение расхода газа весьма незначительно изменяет массовый расход смеси, так как плотность газа намного меньше плотности жидкости. Поэтому массовую скорость смеси рсрис можно считать приблизительно постоянной.
При постоянном расходе Q жидкости перепад давления обратно пропорционален квадрату площади проходного сечения дросселя.
| Принципиальная схема установки для измерения потребляемой мощности калориметрическим.| Схема измерения. |
С помощью вентилей устанавливают постоянный расход жидкости от 10 до 100 сма / сек.
| Бетоносмесительная установка СБ-109. |
Режим движения, характеризующийся постоянным расходом жидкости в течение всего периода следования пробки ( вариант 2), по сути дела уже не представляет собой пробкового, который может перейти в такой режим при изменении условий
Однако, анализируя погрешности измерения расхода, возникающие в этих предельных вариантах структур газожидкостных потоков, мь: определяем величины погрешностей, которые могут иметь место в реальных условиях, что весьма важно для выбора метода измерения расхода жидкой фазы газонасыщенной нефти.
4. Изменение скорости вдоль потока
Средняя скорость
потока определяется так
V
= 
(6.5)
и
при условии Q
= const
(нет присоединений и ответвлений)
скорость тем
больше, чем площадь сечения меньше
(знаменатель
дроби в (6.5) меньше, а сама дробь больше).
Из
(6.5) следует, что расход Q
в данном сечении может быть представлен
в виде произведения
тогда,
выбирая два различных по площади сечения
трубы, рис.6.8, получим
Последнее
уравнение может быть распространено
на любое количество сечений одного и
того же потока, например, на n
разных сечений
Равенство
(6.7), основываясь на свойстве пропорции,
возможно представить так


(6.9)
Из
него следует, что отношение средних
скоростей обратно пропорционально
отношению площадей. Для круглой трубы
площадь сеченияS =
πd2/4
и поэтому скорости в сечениях относятся
обратно пропорционально
квадратам диаметров.
Примеры:
1. Если диаметр трубы увеличить в 2 раза,
то средняя скорость в этом сечении
уменьшится в 4 раза;
2.
Если диаметр трубы в данном сечении
уменьшить
в 3
раза, то средняя скорость в этом сечении
увеличится
в 9 раз.
Задача
6.2.
Скорость в сечении 1
(рис. 6.8) равна 0,8 м/с, диаметр трубы в
сечении 1
равен d1=
50 мм, а Рис.6.8 сечении
2
d2
= 100 мм. Определить скорость в сечении
2.
Решение.
Из условия задачи имеем:
S1
=
= 
Учитывая
(6.9), получаем значение скорости V2
V2
= V1·
= 
V1
= 
0,8
= 0,2 м/с.
6.5. Уравнение
неразрывности в дифференциальной форме
В
потоках несжимаемой жидкости, в которых
нет ни оттока, ни присоединения расхода,
объемный расход в любом сечении
постоянный. Можно поэтому предположить,
что в каждой точке внутри потока должно
выполняться соотношение, гарантирующее,
что в ней не происходит ни исчезновения,
ни возникновения жидкости. Таким
уравнением является уравнение
неразрывности в дифференциальной форме.
Если поток в каждой точке задан вектором
скорости 



то уравнение неразрывности имеет вид



Уравнение
неразрывности должно выполняться в
каждой точке потока жидкости.
Задача
6.3. Скорость
потока задана так
Проверить,
возможно ли существование такого потока.
В выражениях для Ux,Uyи Uz
постоянный коэффициент a
служит для сохранения размерности
скорости в правой части.
Решение.
Подсчитаем
частные производные:

3a; 

Складывая
их, получаем ноль, поэтому уравнение
неразрывности выполняется и такой поток
может существовать.
Подбор оптимального диаметра трубопровода
Определение оптимального диаметра трубопровода – это сложная производственная задача, решение которой зависит от совокупности различных взаимосвязанных условий (технико-экономические, характеристики рабочей среды и материала трубопровода, технологические параметры и т.д.). Например, повышение скорости перекачиваемого потока приводит к уменьшению диаметра трубы, обеспечивающей заданный условиями процесса расход носителя, что влечет за собой снижение затрат на материалы, удешевлению монтажа и ремонта магистрали и т.д. С другой стороны, повышение скорости потока приводит к потере напора, что требует дополнительных энергетических и финансовых затрат на перекачку заданного объема носителя.
Значение оптимального диаметра трубопровода рассчитывается по преобразованному уравнению неразрывности потока с учетом заданного расхода носителя:
При гидравлическом расчете расход перекачиваемой жидкости чаще всего задан условиями задачи. Значение скорости потока перекачиваемого носителя определяется, исходя из свойств заданной среды и соответствующих справочных данных (см. таблицу).
Преобразованное уравнение неразрывности потока для расчета рабочего диаметра трубы имеет вид:
Определение расхода с помощью ротаметра
Ротаметр
относиться к расходомерам обтекания.
Он представляет собой стеклянную трубку,
внутри которой перемещается поплавок
(рис.1.5).
На
поплавок действуют следующие силовые
факторы:
гравитационная
сила mg
(не меняется в зависимости от расхода
и свойств пропускаемой жидкости:
плотности, вязкости);
архимедова
(выталкивающая) сила Rарх
(зависит от массы жидкости, вытесненной
поплавком);
гидродинамическая
сила, обусловленная потоком жидкости,
движущимся с определенной скоростью.
Эта сила зависит от формы поплавка
(степени его обтекания), вязкости
жидкости, адгезионных свойств поверхности
поплавка (степени «прилипания» жидкости
к материалу поплавка) и других трудно
учитываемых факторов.
Раздельное
выделение всех перечисленных выше
силовых факторов затруднительно и
нецелесообразно. Действительно,
независимость гравитационной и
архимедовой сил от расхода означает,
что то или иное положение поплавка будет
определяться только гидродинамической
силой, которая в свою очередь зависит
от расхода, проходящего через ротаметр.
Следовательно, зная положение поплавка
в трубке ротаметра, можно определить
расход жидкости. В лабораторной работе
данная зависимость определяется по
тарировочной кривой Q=Q(h),
где h
– высота
поднятия поплавка.
Внутренняя
поверхность трубки ротаметра имеет
форму правильного конуса*, а поплавок
– форму цилиндра. Тем самым различные
положения поплавка относительно трубки
будут соответствовать разным проходным
сечениям ротаметра.
___________________________________________________________
*Чтобы получить наиболее простую –
близкую к линейной – зависимость между
высотой подъема поплавка и площадью
щели, применяется коническая форма
трубки ротаметра. Угол конусности обычно
составляет 0,5 – 5,5 град.
С
ростом расхода жидкости увеличивается
гидродинамическая сила, действующая
на поплавок, что приводит к перемещению
поплавка вверх и, следовательно,
увеличению площади кольцевого сечения
между поплавком и трубкой. С другой
стороны, увеличение этой проходной
площади приводит к снижению перепада
давлений, действующих на поплавок, и,
значит, к его перемещению в направлении
уменьшения проходной площади щели.
Тем
самым, для каждого значения расхода
будет иметь место такое положение
поплавка, при котором уравновешиваются
силовые факторы, действующие на открытие
и закрытие кольцевой щели.
Стационарное течение жидкости. Уравнение неразрывности
Рассмотрим случай, когда невязкая жидкость течет по горизонтальной цилиндрической трубе с изменяющимся поперечным сечением.
Течение жидкости называют стационарным, если в каждой точке пространства, занимаемого жидкостью, ее скорость с течением времени не изменяется. При стационарном течении через любое поперечное сечение трубы за равные промежутки времени переносятся одинаковые объемы жидкости.
Жидкости практически несжимаемы, т. е. можно считать, что данная масса жидкости всегда имеет неизменный объем. Поэтому одинаковость объемов жидкости, проходящих через разные сечения трубы, означает, что скорость течения жидкости зависит от сечения трубы.
Пусть скорости стационарного течения жидкости через сечения трубы S1 и S2 равны соответственно v1 и v2. Объем жидкости, протекающей за промежуток времени t через сечение S1, равен V1=S1v1t, а объем жидкости, протекающей за то же время через сечение S2, равен V2=S2v2t. Из равенства V1=V2 следует, что
Соотношение (5.10) называют уравнением неразрывности. Из него следует, что
Следовательно, при стационарном течении жидкости скорости движения ее частиц через разные поперечные сечения трубы обратно пропорциональны площадям этих сечений.
Согласно второму закону Ньютона, причиной ускорения является сила. Этой силой в данном случае является разность сил давления, действующих на текущую жидкость в широкой и узкой частях трубы. Следовательно, б широкой части трубы давление жидкости должно быть больше, чем в узкой. Это можно непосредственно наблюдать на опыте. На рис. показано, что на участках разного поперечного сечения S1 и S2 в трубу, по которой течет жидкость, вставлены манометрические трубки.
Как показывают наблюдения, уровень жидкости в манометрической трубке у сечения S1 трубы выше, чем у сечения S2. Следовательно, давление в жидкости, протекающей через сечение с большей площадью S1, выше, чем давление в жидкости, протекающей через сечение с меньшей площадью S2. Следовательно, при стационарном течении жидкости в тех местах, где скорость течения меньше, давление в жидкости больше и, наоборот, там, где скорость течения больше, давление в жидкости меньше. К этому выводу впервые пришел Бернулли, поэтому данный закон называется законом Бернулли.
Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:
ρ — плотность жидкости,
v — скорость потока,
h — высота, на которой находится рассматриваемый элемент жидкости,
Константа в правой части обычно называется напором, или полным давлением. Размерность всех слагаемых — единица энергии, приходящейся на единицу объёма жидкости.
Это соотношение называют уравнением Бернулли. Величина в левой части имеет отношение к интегралу Бернулли.
Согласно закону Бернулли полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока. Полное давление состоит из весового, статического и динамического давления. Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает. Закон Бернулли справедлив и для ламинарных потоков газа. Явление понижения давления при увеличении скорости потока лежит в основе работы различного рода расходомеров, водо- и пароструйных насосов.
Закон Бернулли справедлив в чистом виде только для жидкостей, вязкость которых равна нулю, то есть таких жидкостей, которые не прилипают к поверхности трубы. На самом деле экспериментально установлено, что скорость жидкости на поверхности твердого тела всегда в точности равна нулю.
Закон Бернулли можно применить к истечению идеальной несжимаемой жидкости через малое отверстие в боковой стенке или дне широкого сосуда.
Согласно закону Бернулли приравняем полные давления на верхней поверхности жидкости и на выходе из отверстия:
p — атмосферное давление,
h — высота столба жидкости в сосуде,
v — скорость истечения жидкости.
Относительный расход — жидкость
Относительный расход жидкости /, умноженный на максимальный расход ее через клапан, равен действительному расходу жидкости через клапан. Следовательно, коэффициент передачи клапана является функцией действительного расхода жидкости и не зависит от размеров клапана. Это одна из причин, обусловивших широкое использование клапанов с логарифмической характеристикой.
| Общий вид зависимостей qf ( x. |
По оси ординат здесь отложен относительный расход жидкости в ядре потока x3 G K / GCM. МВт / м2, при паросодержаниях, близких к граничным, кривые Xa f ( x) выходят на горизонтальные линии.
На рис. 2.23 показано изменение относительного расхода жидкости в пленке xz, равное отношению расхода жидкости в пленке т2 к общему расходу смеси в канале. На графике по оси абсцисс дается массовое расходное паросодержание жп. В проведен комплекс экспериментальных работ по дисперсно-кольцевому режиму течения в диапазоне давлений от 4 0 до 7 0 МПа и удельных массовых расходов 500 — 4000 кг / м2 — с и расходных паросодержапий х от 0 1 до 0 9 в трубах диаметром 13 3 мм.
| Зависимость / от т для трубопровода с клапаном, имеющим логарифмическую характеристику, при различных отношениях С0 / Св. |
На рис. П-6 дан график зависимости относительного расхода жидкости от положения штока клапана, который при постоянном Ар совпадает с графиком зависимости относительного открытия клапана от относительного положения штока. В частности, у клапана с линейной характеристикой относительное открытие прямо пропорционально относительному положению штока.
| Осредненные зависимости тем — Осредненные зависимости пов добычи нефти Гн и обводненности нефтеотдачи г от относительного от-добываемой продукции Ьв от нефтеотдачи пластов т при различной вязкости. |
Эта зависимость показывает, при каком относительном расходе жидкости ( воды) получена конкретная нефтеотдача пластов. Удельный расход жидкости или объем нагнетаемой воды на единицу добываемой нефти служит показателем эффективности заводнения залежей.
| Соотношение между скоростью газового потока V, расходом жидкости L и перепадом давления ДР в насадочной колонне.| I Характеристика наиболее распространенных насадок. |
В табл. 6.5 приведены результаты вычислений значений относительного рабочего расхода Qp / QHac в зависимости от относительного давления ( ре-рн) / Рнас и относительного расхода жидкости во вспомогательном контуре х Фн / Фнас-Порядок вычислений следующий.
| Зависимость медианного диаметра. |
Заданный расход — жидкость
Заданный расход жидкости обеспечивается поддержанием необходимого постоянного перепада давления на штуцере 11 ( контролируется по манометрам 10, 12) благодаря изменению степени открытия запорного устройства 16 на линии сбора жидкости.
Заданный расход жидкости и дисперсность обеспечиваются установкой различного количества распылителей на штангах. Чем меньше размер отверстий, тем мельче дробится жидкость. При небольших секундных расходах часть распылителей заменяют заглушками. Чтобы избежать подтекания жидкости из распылителей, после закрытия клапана в штуцерах распылителей устанавливают отсечные клапаны ниппельного типа. Кроме того, применяют инжекторное устройство для отсоса жидкости из штанг в специальные бачки с последующей перекачкой в бак опрыскивателя.
| Основные технические данные самолетов и вертолетов. |
Заданный расход жидкости и дисперсность обеспечиваются установкой различного количества распылителей на штангах и их отверстиями. При небольших расходах часть распылителей заменяют заглушками. Жидкость в баке перемешивается гидромешалкой. Для высокотоксичных пестицидов предназначен отдельный выносной бачок на внешней стенке фюзеляжа в задней части самолета. В этом случае вода и препарат подаются в насос раздельно.
Заданный расход жидкости и дисперсность обеспечивают установкой различного количества распылителей на штангах, а сыпучих материалов и порошкообразных пестицидов — изменением зазора между дисками и стенками горловины. Открытие заслонки в горловине, управление ветряков, открытие и закрытие клапана при опрыскивании осуществляется пневматически.
Заданный расход жидкости контролируется с помощью уровнемера, подключенного к одному из сосудов.
При заданном расходе жидкости нижней границей скорости газа, отвечающей кольцевому режиму течения, является скорость газа, при которой происходит образование жидкостных перемычек, предшествующих переходу к снарядному режиму течения. Верхним пределом скорости газа является ее значение, при котором кольцевой режим течения переходит в дисперсно-кольцевой.
При заданном расходе жидкости и соответствующем перепаде давления рычаг под воздействием разности усилий, развиваемых сильфонами, перемещается вверх и головкой регулировочного болта нажимает на шток микропереключателя. При этом подается электрический сигнал, свидетельствующий о наличии заданного расхода жидкости. Настройка реле на срабатывание при заданном перепаде давления ( расходе) осуществляется изменением поджатия пружины.
| Характеристики ВЗД. а — идеальная. б — реальная. |
При заданном расходе жидкости и контурном диаметре РО кинематическое отношение оказывает определяющее влияние на характеристики ВЗД ( разд.
При известном или заданном расходе жидкости в равенство ( 9) ( подставляем значение капиллярной проницаемости из ( 3) или из ( 4) в зависимости от вязкости фильтрующейся жидкости. После этого из равенства ( 9) определяем величину градиента давления. Затем по известной величине градиента давления из равенства ( 3) или ( 4) определяем величину капиллярной проницаемости.
Максимально возможное при заданном расходе жидкости Q м / ч число точек для таких оросителей можно найти по формуле ( 39) расхода через единичный перелив ( гл.
Действительно, при сохранении заданного расхода жидкости уменьшение относительного радиуса т связано с увеличением главного параметра А. В уравнении ( 91) это влияет на уменьшение отношения Z / A, характеризующего увеличение торможения жидкости в камере закручивания форсунки. Далее, с уменьшением значения t множитель ( 2 Як — PI — т) увеличивается, что приводит к уменьшению отношения Z / A. Следует также отметить, что в первом приближении PI T. Множитель ( 2 Як — PI — т) увеличивается и с увеличением Як ( относительной длины камеры закручивания), что тоже приводит к уменьшению камеры закручивания при заданном диаметре сопла и ухудшению дисперсности жидкости.
Объемный расход
Объемный расход равен произведению площади сечения на скорость потока. Физические явления, лежащие в основе измерения расхода, могут быть связаны с изменением как скорости движения вещества, так и его количества.
Объемный расход равен произведению площади проходного сечения на скорость потока. Физические явления, лежащие в основе измерения расхода, могут быть связаны с изменением как скорости движения вещества, так и его количества.
Объемный расход через каждый канал вентиляционного тракта равен объемному количеству газа, проходящему в единицу времени через поперечное сечение данного канала.
Объемный расход — объемное количество жидкости или газа, протекающее в единицу времени через поперечное сечение потока; единица измерения в СИ и МКС м / сек, в СГС см3 / сек.
Объемный расход ( количество жидкости, проходящее каждую секунду через поперечное сечение струи) в силу непрерывности потока должен оставаться постоянным на протяжении всей струи.
Объемный расход и температура подаваемой в него реакционной смеси составляют F, м3 / с и Тж, К, а концентрация реагирующего вещества равна QH. К и концентрация реагирующего компонента Q имеют одинаковые значения. Поток из реактора выходит с теми же значениями величин. Плотности р, кг / м3 исходного и прореагировавшего веществ одинаковы. Удельные теплоемкости с, Дж / ( кг-град) продуктов на входе и выходе из реактора равны между собой. Объем реакционной массы V, м3, постоянен.
Объемный расход ( количество циркулирующего) воздуха составляет 60000 м / ч — в единицах СИ 60000 — 278 1Q — 6 16 7 мг / сек.
Объемный расход через лопаточный канал можно разделить на равное число частей, соответствующее желаемому числу линий тока. Тогда получим уточненную картину линий тока в лопаточном канале, которую можно принять за основу для второго расчета.
Объемный расход в измерительных линиях и суммарный по узлу учета.
Объемный расход — физическая величина ( qt), равная отношению объема вещества V, проходящего через поперечное сечение к промежутку времени /, в течение которого объем проходит.
Объемный расход остается неизменным и движение предполагается, ламинарное.
Объемный расход какой-либо из фаз, отнесенный к площади поперечного сечения потока, называется приведенной скоростью этой фазы.
3. Расход жидкости и средняя скорость
При
течении реальной (вязкой) жидкости
скорости по сечению канала неодинаковы
(на стенках они равны нулю); поэтому в
инженерных расчетах применяют среднюю
скорость, которая определяется так

где
Q
– расход жидкости; S
– площадь поперечного сечения потока.
В
данном случае имеется в виду объемный
расход, который может выражаться в м3/с,
л/с, см3/с,
и т.д., между которыми устанавливаются
соотношения: 1,0 м3/с
= 1,0·103
л/с = 1000 л/с = 1000 дм3/с
= 1000·1000 см3/с
= 1,0·106
см3/с.
Это следует из
равенств
Задача
6.1. Определить
среднюю скорость воды в трубе диаметром
d
= 50 мм, если расход Q
равен Q
= 4 л/с.
Решение.
Расход Q
= 4 л/с = 4000 см3/с,
диаметр d
= 50 мм = 5 см,
S
= πd2/4
– площадь сечения круглой трубы. Средняя
скорость потока в соответствии с (6.4)
V
= 
= 
= 
Объёмный метод измерения расхода
Объёмный метод измерения расхода основан
на вытеснении определённых объёмов
жидкости из измерительной камеры прибора
овальными шестернями, находящимися в
зубчатом зацеплении и вращающимися под
действием разности давлений на входном
и выходном патрубках прибора. Такие
расходомеры называют счётчиками.
Мерой расхода является число циклов
вытеснения жидкости.
Диаметр трубопроводов 15-300 мм. Температура
среды до 150°С. Давление до 10 МПа.
Достоинством является
стабильность показаний.
Недостатки:
необходимость установки фильтров,
задерживающих твердые частицы
(чувствительный элемент при их
проникновении может выйти из строя);
износ движущихся деталей, приводящий
к увеличению погрешности показаний,
которая обычно составляет 0,5-1,0% от
измеряемой величины.
Схема счётчика приведена на рисунке. В
первом исходном положении (рисунок а)
поверхность (г-а) шестерёнки 2 находится
под давлением поступающей жидкости, а
равная ей поверхность (в-г) – под давлением
выходящей жидкости, меньшим входного.
Эта разность давлений создаёт крутящий
момент, вращающий шестерню 2 по часовой
стрелке. Причём жидкость из полости 1 и
полости, расположенной под шестерней
3, вытесняется в выходной патрубок.
Крутящий момент шестерни 3 равен нулю,
так как поверхности (а-1-г-1) и (г-1-в-1) равны
и находятся под одинаковым входным
давлением. Следовательно, шестерня 2 –
ведущая, шестерня 3 – ведомая.
В
промежуточном положении (рисунок б)
шестерня 2 вращается в прежнем направлении,
но её крутящий момент будет меньше, чем
в положении (рисунок а), из-за
противодействующего момента, созданного
давлением на поверхность (д-г) (д – точка
контакта шестерней). Поверхность
(а-1-в-1) шестерни 3 находится под давлением
входящей, а поверхность (в-1-б-1) под
давлением выходящей. Шестерня испытывает
крутящий момент, направленный против
часовой стрелки. В этом положении обе
шестерни ведущие.
Во втором исходном положении (рисунок
в) шестерня 3 находится под действием
наибольшего крутящего момента и является
ведущей, в то время как крутящий момент
шестерни 2 равен нулю, она ведомая. Однако
суммарный крутящий момент обеих шестерен
для любого из положений остаётся
постоянным.
За время полного оборота шестерён (один
цикл работы счётчика) полости 1 и 4 два
раза заполняются и два раза опорожняются.
Объём четырёх доз жидкости, вытесненных
из этих полостей, и составляет измерительный
объём счётчика.
Чем больше расход жидкости через счётчик,
тем с большей скоростью вращаются
шестерни, вытесняя отмеренные объёмы.
Передача от овальных шестерён счётному
механизму осуществляется через магнитную
муфту, которая работает следующим
образом. Ведущий магнит укреплён в торце
овальной шестерни 3, а ведомый на оси,
связывающей муфту редуктором 5. Камера,
где расположены овальные шестерни,
отделена от редуктора 5 и счётного
механизма 6 немагнитной перегородкой.
Вращаясь, ведущий вал увлекает за собой
ведомый.