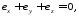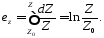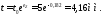что такое объемная деформация

Деформация объёмная

Деформация объёмная – относительное изменение объёма тела в точке, равное сумме линейных деформаций по трём осям.
[Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)]

Полезное

Смотреть что такое «Деформация объёмная» в других словарях:

деформация объёмная — Относительное изменение объёма тела в точке, равное сумме линейных деформаций по трём осям [Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)] Тематики строительные изделия прочие EN cubic strainvolumetric strain DE… … Справочник технического переводчика

ДЕФОРМАЦИЯ ОБЪЁМНАЯ — относительное изменение объёма тела в точке, равное сумме линейных деформаций по трём осям (Болгарский язык; Български) обемна деформация (Чешский язык; Čeština) objemová deformace (Немецкий язык; Deutsch) Volumenverformung (Венгерский язык;… … Строительный словарь

объёмная деформация — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN volume strain … Справочник технического переводчика

объёмная деформация горных пород — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN volumetric rock deformation … Справочник технического переводчика

объёмная деформация — tūrinė deformacija statusas T sritis fizika atitikmenys: angl. three dimensional strain; volume strain vok. räumliche Deformation, f; räumliche Verformung, f rus. объёмная деформация, f; пространственная деформация, f pranc. déformation de volume … Fizikos terminų žodynas

относительная объёмная деформация — Отношение уменьшения объёма к первоначальному объёму при всестороннем сжатии [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN volumetric deformation … Справочник технического переводчика

пространственная деформация — tūrinė deformacija statusas T sritis fizika atitikmenys: angl. three dimensional strain; volume strain vok. räumliche Deformation, f; räumliche Verformung, f rus. объёмная деформация, f; пространственная деформация, f pranc. déformation de volume … Fizikos terminų žodynas

Деформации материалов — Термины рубрики: Деформации материалов Воздействие Деформативность Деформации Деформации неупругие Деформации относительные … Энциклопедия терминов, определений и пояснений строительных материалов

Пластичность — I Пластичность (от греч. plastikós годный для лепки, податливый, пластичный) свойство твёрдых тел необратимо изменять свои размеры и форму (т. е. пластически деформироваться) под действием механических нагрузок. П. кристаллических тел… … Большая советская энциклопедия

Пластичность (свойство твёрдых тел) — Пластичность (от греч. plastikós ‒ годный для лепки, податливый, пластичный), свойство твёрдых тел необратимо изменять свои размеры и форму (т. е. пластически деформироваться) под действием механических нагрузок. П. кристаллических тел (или… … Большая советская энциклопедия

Источник

2.3. Объемная деформация

После деформации длины ребер будут

и их произведение дает новый, измененный объем. Представим каждое из новых слагаемых в виде

d V + δ d V = d x ( 1 + ε 1 ) d y ( 1 + ε 2 ) d y ( 1 + ε 3 ) =

Здесь δ d V – изменение объема при деформации.

Так как сами величины ε i – бесконечно малые величины, их произ-

конечно малыми высших порядков. Тогда новый объем можно представить, как

d V + δ d V = d V ( 1 + ε 1 + ε 2 + ε 3 )

к первоначальному объему называется

относительным изменением объема и обозначается как θ

Подставим в выражение для θ значения относительных деформаций ε i через напряжения из обобщенного закона Гука

[ σ 1 −µσ 2 −µσ 3 + σ 2

[ σ 1 + σ 2 + σ 3 − 2 µ ( σ 1

Учитывая, что сумма нормальных напряжений на любых взаимно перпендикулярных площадках – величина постоянная, можно записать относительное изменение объема через напряжения по любым взаимно перпендикулярным площадкам

При пространственном, сферическом, напряженном состоянии материала, когда напряжения в точке равны

σ 0 = σ 1 = σ 2 = σ 3 ≠ 0;

В случае чистого сдвига при

При чистом сдвиге изменяется только форма, а объем остается неизменным.

2.4. Потенциальная энергия упругой деформации

Из диаграммы растяжения упругопластичного материала (см. раздел «Определение механических характеристик материалов») видно, что на участке ОА диаграммы в материале стержня, подвергаемого растяже-

нию, накапливается потенциальная энергия упругой деформации.

Величина ее для стержня в целом может быть определена как пло-

щадь треугольника в координатах P − ∆ l

Если найти удельную потенциальную энергию, то она в координа-

тах ε − σ будет равна u =

. Здесь величина ε заменена на

Это потенциальная энергия упругой деформации, приходящаяся на единицу объема при одноосном напряженном состоянии. Для объемного напряженного состояния полная удельная потенциальная энергия упругой

деформации может быть найдена как

Заменяя значения ε i на напряжения σ i

по обобщенному закону Гу-

[ σ 1 2 + σ 2 2 + σ 3 2 − 2 µ ( σ 1 σ 2

В общем случае напряженного состояния материала происходит изменение объема под действием нормальных напряжений и изменение формы под действием касательных напряжений. Следовательно, можно считать, что полная потенциальная энергия состоит из двух слагаемых:

где u об – часть потенциальной энергии, накапливаемой при измене-

нии объема; и ф – часть потенциальной энергии, накапливаемой при изменении формы.

Рассмотрим элемент материала в виде квадрата со стороной а (бесконечно малых размеров).

Пусть деформация – сдвиг стороны ВС – ∆ S (здесь вся деформа-

ция сведена к сдвигу одной стороны); ∆ S – абсолютная деформация при сдвиге или абсолютный сдвиг (рис.13).

Отношение ∆ l l = ε – относительная деформация при растя-

просто γ – относительная деформация сдвига.

Так как сдвиг – плоское напряженное состояние, используем закон

Здесь, согласно закону парности касательных напряжений и усло-

тельные и знак минус на плюс.

Величина ( E ) = G носит название модуль упругости при сдви- 2 1 + µ

ге. Он связывает три упругие постоянные характеристики материала в одно целое.

Для стали G = 8 10 5 кг/см 2 или 8 10 4 Mпа. Выражение τ = G γ – закон Гука при сдвиге.

Таким образом, основываясь на представлениях об объемной деформации, можно считать, что потенциальная энергия упругой деформации, накапливаемая при изменении объема, эта та часть энергии, которая создается одинаковыми нормальными напряжениями по трем ортогональным площадкам. Будем считать, что это среднее напряжение из трех главных

Тогда удельная потенциальная энергия, идущая на изменение объ-

или, что тоже для любого направления

тенциальной энергии, получим

[ ( σ 1 − σ 0 ) 2 + ( σ 2 − σ 0 ) 2 + ( σ 3 − σ 0 ) 2 −

− 2 µ [ ( σ 1 − σ 0 )( σ 2

− σ 0 ) + ( σ 1 − σ 0 )( σ 3

− σ 0 ) + ( σ 2 − σ 0 )( σ 3

После преобразования и замены σ 0 на

(плоского) напряженного состояния, принимая

Для площадок, произвольно ориентированных в пространстве, необходимо учесть действие касательных напряжений, то есть

( σ 2 x + σ 2 y + σ x σ y ) +

2.5. Исследование напряженного состояния материала графиче-

При экспериментальном изучении напряженного состояния реальных конструкций или моделей ответственных элементов конструкций, например, в судостроении, авиации широко используется тензометрия [7], [8].

Для обработки результатов замеров и анализа полученных данных удобно пользоваться графическим методом исследования напряженного состояния материала.

Суть этого метода заключается в следующем.

Если на координатных осях y ≡ τ и x ≡ σ построить окружность

ный, опирающийся на ту же дугу окружности, что и

Источник

Виды деформаций деталей: растяжение, сжатие, сдвиг, кручение, изгиб

материал предоставил СИДОРОВ Александр Владимирович

Деформация – изменение формы, размеров тела под действием приложенных к нему сил.

Линейная деформация – изменение линейных размеров тела, его рёбер. Линейные размеры тела могут изменяться одновременно в одном, двух или трёх взаимно перпендикулярных направлениях, что соответствует линейной, плоской и объёмной деформации. Линейная деформация, как правило, сопровождается изменением объёма тела.

Угловая деформация – изменение угловых размеров тела, углов наклона его граней. В результате угловой деформации происходит взаимное смещение граней. При этом изменяется только форма тела, объём сохраняется неизменным.

Линейная деформация связана преимущественно с действием нормальных напряжения, угловая – с действием касательных напряжений. [1]

Растяжение (сжатие) – деформация, возникающая под действием в поперечном сечении только продольной (растягивающей или сжимающей) силы.

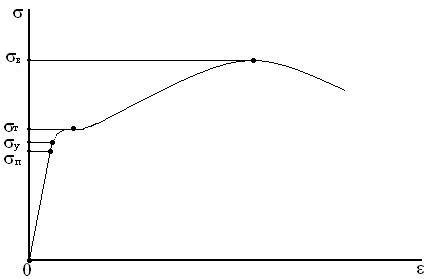
Напряжение вдоль оси прямо пропорционально растягивающей (сжимающей) силе и обратно пропорционально площади поперечного сечения. При упругой деформации соотношение между напряжением и относительной деформацией определяется законом Гука, при этом поперечные относительные деформации выводятся из продольных путём умножения их на коэффициент Пуассона. Пластическая деформация, предшествующая разрушению части материала, описывается нелинейными законами (рисунок 1). [2]

Рисунок 1 – Диаграмма растяжения

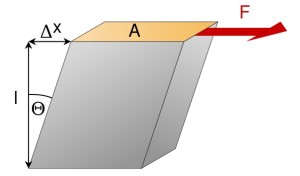
Сдвиг – деформация, характеризующаяся взаимным смещением параллельных слоёв материала под действием сил, приложенных касательно к его поверхности, при неизменном расстоянии между слоями (рисунок 2).

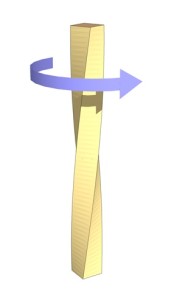
Кручение – деформация, характеризующаяся взаимным поворотом поперечных сечений тела под действием пары сил (момента) в этих сечениях (рисунок 3).

Рисунок 3 – Кручение

Изгиб – деформация, при которой происходит изменение кривизны осей тела под действием изгибающих моментов в поперечных сечениях (рисунок 4).

Источник

2.8. Большие деформации

В процессах обработки металлов давлением полная деформация может достигать- значительной величины. Для ее описания рассмотрим параллелепипед с ребрами, параллельными главным осям деформаций, и с исходными размерами до пластической деформации X₀, Y₀ и Z₀ (рис. 40, а).

Пусть этот параллелепипед после однородной деформации (рис. 40,б) останется также параллелепипедом и конечные размеры его будут: X, У, Z. Тогда по условию постоянства объема

или сумма трех главных деформаций равна нулю:

где(23)

Логарифмическая деформация представляет собой интеграл бесконечно малого приращения данного размера тела или его элемента, отнесенного к его величине в каждый данный момент деформации. Например, в направлении ребра Z cyммapнaя относи­тельная деформация при осадке от Z₀ до Z составит:

Аналогичные деформации в направлении ширины и длины соответственно равны:

В случае однородной деформации логарифмические деформации представляют собой результат суммирования бесконечно малых деформаций, поэтому их часто называют истинными деформа­циями.

Логарифмические деформации обладают свойством аддитивности: их можно складывать при определении суммарной деформации, осуществленной за несколько операций.

Допустим, что растяжение образца длиной 100 мм произведено в два этапа. Вначале образец был растянут на длину 120 мм, а после до 150 мм.

Суммарная деформация за два этапа нагружения

Таким образом,

Степень деформации тел можно выразить иначе, а именно, как отношение приращения размера к начальному размеру тела:

(24)

Величины е и ε связаны между собой:

(25)

Формулы (24) часто используют в процессах обработки металлов давлением для расчета относительного обжатия, уширения, вытяжки. Например, величина относительного обжатия при осадке

Граница между деформациями, рассчитываемыми по формулам (23) и (24), зависит от той точности, с которой рассчитывается процесс. Истинные и относительные деформации вначале близки между собой, а затем расходятся (рис. 41).

Задача 13. Плита длиной 1200мм, шириной 360мм и толщиной 5мм растягивается равномерно при растяжении в продольном направлении до тех пор, пока ее длина не увеличится до 1440мм без изменения ширины. Найти: а) конечные главные деформации, б) конечные размеры плиты.

Выбрав следующие направления осей: длина х, ширина у, толщина z, получаем:

Из уравненияполучаем

Следовательно, размеры плиты после деформации будут следующими: длина 1440 мм, ширина 360 мм и толщина 4,16 мм.

2.9. Объемная деформация

При деформации тела под действием внешних сил изменяется не только форма, но и объем. Изменение объема, отнесенное к начальному объему, называется относительной объемной деформацией. Изменение объема происходит в основном вследствие изменения длин ребер элементарного параллелепипеда.

Выделим в рассматриваемом теле элементарный параллелепипед с ребрами dx,dy,dz, параллельными главным направлениям 1,2,3 в данной точке. В этом случае при деформировании углы парал­лелепипеда остаются прямыми, изменятся лишь дайны ребер и станут равными

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

ДЕФОРМАЦИЯ

Смотреть что такое ДЕФОРМАЦИЯ в других словарях:

ДЕФОРМАЦИЯ

(мех.) — есть изменение формы тела или частей его, изменение строения тела. Д. могут быть сплошными или разрывными. Сплошные Д. суть такие, при которых всякая непрерывная линия, проведенная через точки тела, остается непрерывной во время деформирования, хотя изменяет положение в пространстве, свой вид и размеры. Движение такого тела может быть выражено такими равенствами:

Вид этих уравнений не зависит от выбора точки К; значит, если вокруг двух различных точек тела выделить одинаковые по виду, размерам и положению объемы вещества, то Д.этих двух объемов будут тожественны и выразятся одними и теми же уравнениями (F). Таким образом A, B, C представляют поступательное движение тела, а остальные члены вторых частей равенств (E) или вторые часта равенств (F), выражают однородную Д. вокруг всякой точки тела.

При однородной Д., выражаемой уравнениями:

1 ξ, у = Е 2 η, z = Е 3 ζ

все точки, находившиеся в начальный момент в плоскостях координат и на осях координат, остаются при Д. на тех же плоскостях и осях; такая однородная Д. может быть рассматриваема как результат трех однородных удлинений или сжатий параллельно этим осям; каждая единица длины, параллельная оси х-ов, удлиняется при этом на величину 

соответственные удлинения единиц длины, параллельных прочим двум осям, будут:

ε 2 = E 2 — 1, ε 3 = E 3 — 1

а кубичное расширение единицы объема вещества равняется

Примером однородной Д., сопровождаемой вращением, может служить так называемый сдвиг, напр. параллельно плоскости yz, выражающийся следующими уравнениями:

x = ξ, y = g ξ + η, z = ξηζ.

При этой Д. плоскость yz остается неподвижной; все плоскости, ей параллельные, сдвигаются параллельно оси y-ов на длины, пропорциональные их расстояниям от нее (т. e. пропорциональные ξ), причем прямые, первоначально параллельные оси x-ов, становятся наклонными к ней под углом, тангенс которого равен g. В момент t = 0 главная ось наибольшего расстояния составляет с положительной осью х-ов угол (π /4 — ψ/ 2) и угол (π /4 + ψ/ 2) с положительной осью y-ов; другая главная ось (ось наибольшего сжатия) к ней перпендикулярна, третья главная ось параллельна оси z-ов и сохраняет свое направление. Д. сопровождается вращением вокруг оси z-ов на угол ψ, где tg ψ равен половине g. Если произвести один за другим два сдвига одинаковой величины, один только что упомянутый, а другой параллельно плоскости zx по направлению оси x (с таким же коэффициентом g), то в результате этих двух сдвигов получится так называемый двойной сдвиг в плоскости xy; это — чистая Д. и величина 2g называется коэффициентом такого двойного сдвига.

y = η + В(1 — ξ 2 /a 2 )t.

Жидкость течет между двумя стенками, параллельными плоскости yz и отстоящими от нее на расстоянии а по обе стороны ее; все точки движутся прямолинейно параллельно оси у-ов со скоростями постоянными и тем большими, чем точки ближе к средней плоскости yz. При этой Д. все точки жидкости, находившиеся в момент t = 0 в плоскости, перпендикулярной к оси у-ов, в момент t будут находиться на параболическом цилиндре, между тем как при однородной Д. всякая плоскость остается плоскостью.

тела под влиянием действующих на него внешних сил служит основанием современной теории строительной механики, с помощью которой вычисляется сопротивление материалов и определяются напряжения частей сложных сооружений, а следовательно, и потребные их размеры. При этом принцип производной работы Д. применяется для определения перемещения точек упругих систем. Всякое твердое тело рассматривается как система материальных точек, связанных между собой частичными, внутренними силами. Из внешних сил, могущих действовать на тело, рассматриваются сопротивления опор и разного рода нагрузки, приложенные в точках поверхности тела, и сила тяжести и другие подобные силы, действующие на частицы его массы независимо от поверхности. Всякая внешняя сила производит Д. тела, которая по удалении силы более или менее исчезает. Внутренние силы, стремящиеся восстановить первоначальную форму тела, измененную внешними силами, называются силами упругости. Та часть видоизменения тела, которая исчезает по прекращении действия внешних сил, называется упругим, а остальная часть — остающимся, или постоянным видоизменением. В обычных теоретических выводах строительной механики рассматриваются условия равновесия внутренних сил упругости с внешними силами только до тех пределов этих сил, при которых постоянных видоизменений вовсе не происходит или, во всяком случае, такие видоизменения не замечаются. Теория сопротивления материалов рассматривает только твердые тела, изменения которых под действием внешних сил имеют место по отношению как объема их, так и самого вида тел (в жидких телах изменяется только вид тела). Если внешние силы, действующие на тело, возрастают от нуля постепенно, то и изменение формы тела увеличивается мало-помалу. В случае внезапного приложения или отнятия силы, а также в случае не вполне постепенного изменения сил, тело испытывает колебания или качания около формы покоя, амплитуда которых постепенно уменьшается, пока тело наконец не примет окончательной формы равновесия. Сила упругости, проявляющаяся при Д. тела, всегда противоположна направлению перемещения частиц. Внутренние силы исполняют при видоизменении, произведенном внешними силами, отрицательную работу. Сумма работ всех этих сил и есть совокупная работа деформации, равная по величине и обратная по знаку работе внешних сил, а при неподвижных опорах — работе нагрузки. В зависимости от рода действия внешних сил, внутренние силы сопротивления могут быть растягивающие (см. Растяжение), сжимающие (см. Сжатие) и скалывающие (см. Скалывание). При данной форме твердого тела, определенном числе и расположении опор и данных по величине, направлениям и точкам приложения внешних сил (нагрузок) напряжения в частях тела определяются, на основании теории упругости, из условия равенства работы внутренних сил сопротивления при Д. тела работе внешних сил (см. Изгиб). Этим же принципом пользуются для расчета сложных систем (сочлененных), для чего с удобством можно пользоваться началом производной работы Д.

ДЕФОРМАЦИЯ

(от лат. deformatio — искажение) изменение относительного положения частиц тела, связанное с их перемещением. Д. представляет собой результат из. смотреть

ДЕФОРМАЦИЯ

деформация ж. 1) Изменение размеров, формы твердого тела под действием внешних сил (обычно без изменения его массы). 2) Любое изменение, отклонение чего-л. от нормы.

ДЕФОРМАЦИЯ

ДЕФОРМАЦИЯ

ДЕФОРМАЦИЯ

ДЕФОРМАЦИЯ

Деформация (мех.) — есть изменение формы тела или частей его, изменение строения тела. Д. могут быть сплошными или разрывными. Сплошные Д. суть такие, при которых всякая непрерывная линия, проведенная через точки тела, остается непрерывной во время деформирования, хотя изменяет положение в пространстве, свой вид и размеры. Движение такого тела может быть выражено такими равенствами: где ξ, η, ζ суть координаты какой-либо точки тела в момент t = 0 (начальные координаты), x, y, z — координаты ее же в момент t; f₁, f_2, f₃ — сплошные функции четырех переменных: ξ, η, ζ, t. Например, уравнения: где А ₁, А ₂ А ₃ А, В ₁. C суть какие-либо непрерывные функции времени, выражают деформации, называемые однородными. Они имеют следующие свойства: 1) всякие две взаимно подобные и подобно расположенные фигуры, начерченные в теле в какой-либо момент, изменяя при однородной Д. свой вид, размеры и положение в пространстве, будут все-таки сохранять свое взаимное подобие, причем центром подобия будет все время служить та самая точка тела, которая была им в начале; 2) плоскости и прямые не искривляются; 3) представим себе неизменяемую среду, движущуюся поступательно вместе с какой-либо из точек тела; пусть это будет точка К; проведем через нее координатные оси, параллельные неподвижным и неизменно связанные с этой средой; назовем через ξ ‘, η‘, ζ‘ начальные координаты прочих точек тела относительно этих осей, а через x‘, у‘, z‘ координаты их в момент t; тогда окажется, что относительное движение деформируемого тела по отношению к неизменяемой среде выразится уравнениями: Вид этих уравнений не зависит от выбора точки К; значит, если вокруг двух различных точек тела выделить одинаковые по виду, размерам и положению объемы вещества, то Д. этих двух объемов будут тожественны и выразятся одними и теми же уравнениями (F). Таким образом A, B, C представляют поступательное движение тела, а остальные члены вторых частей равенств (E) или вторые часта равенств (F), выражают однородную Д. вокруг всякой точки тела. При однородной Д., выражаемой уравнениями: х = Е ₁ ξ, у = Е ₂ η, z = Е ₃ ζ все точки, находившиеся в начальный момент в плоскостях координат и на осях координат, остаются при Д. на тех же плоскостях и осях; такая однородная Д. может быть рассматриваема как результат трех однородных удлинений или сжатий параллельно этим осям; каждая единица длины, параллельная оси х-ов, удлиняется при этом на величину  ε ₁ = Е ₁ — 1; соответственные удлинения единиц длины, параллельных прочим двум осям, будут: ε ₂ = E₂ — 1, ε ₃ = E₃ — 1 а кубичное расширение единицы объема вещества равняется θ = Е ₁ Е ₂ Е ₃ — 1. При всякой однородной Д. можно найти три такие взаимно ортогональные направления, которые хотя и изменяются в пространстве, но все-таки остаются взаимно ортогональными, так что, вообще говоря, Д. сопровождается вращением. Эти направления называются главными осями однородных Д. Если вращений нет, то направления главных осей остаются неизменными, и тогда однородная Д. называется чистой. Д. x = Е ₁ ξ, у = Е ₂ η, z = Е ₃ ζ есть чистая Д., главные оси которой параллельны осям координат. Если составить уравнения чистой Д., главные оси которой не параллельны осям координат, то окажется, что в этих уравнениях коэффициент В ₁ тожественен с А ₂, C₁ с А ₃ и C₂ с B₃. Примером однородной Д., сопровождаемой вращением, может служить так называемый сдвиг, напр. параллельно плоскости yz, выражающийся следующими уравнениями: x = ξ, y = g ξ + η, z = ξηζ. При этой Д. плоскость yz остается неподвижной; все плоскости, ей параллельные, сдвигаются параллельно оси y-ов на длины, пропорциональные их расстояниям от нее (т. e. пропорциональные ξ), причем прямые, первоначально параллельные оси x-ов, становятся наклонными к ней под углом, тангенс которого равен g. В момент t = 0 главная ось наибольшего расстояния составляет с положительной осью х-ов угол (π /4 — ψ/2) и угол (π /4 + ψ/2) с положительной осью y-ов; другая главная ось (ось наибольшего сжатия) к ней перпендикулярна, третья главная ось параллельна оси z-ов и сохраняет свое направление. Д. сопровождается вращением вокруг оси z-ов на угол ψ, где tg ψ равен половине g. Если произвести один за другим два сдвига одинаковой величины, один только что упомянутый, а другой параллельно плоскости zx по направлению оси x (с таким же коэффициентом g), то в результате этих двух сдвигов получится так называемый двойной сдвиг в плоскости xy; это — чистая Д. и величина 2g называется коэффициентом такого двойного сдвига. Теория однородных Д. играет существенную роль в гидродинамике и теории упругости, так как там рассматриваются такие Д. тел, при которых вокруг каждой точки тела, в ближайшем соседстве ее, совершаются относительные Д. однородные и ничтожно малые, т. e. такие, у которых коэффициенты A₁, B₂, C₃ разнятся от единицы на ничтожно малые величины, а коэффициенты A₂, A₃, B₁, B₃, C₁ и C₂ ничтожно малы. Поэтому теорию таких Д. можно найти в соч. по вышесказанным предметам, напр.: «Kirchhoff‘s «Vorlesungen über mathematische Physik»; Ibbetson, «Treatise on the mathematical Theory af perfectly elastic solids»; Thomson and Tait, «Treatise on natural Philosophy» и т. д. Из числа неоднородных Д. нужно упомянуть о подобно-изменяющей Д. и коллинеарной Д., теории которых разрабатываются некоторыми авторами за границей и у нас (проф. П. И. Сомов, Д. Н. Зейлигер). Примером неоднородной, но еще сравнительно простой Д. может служить движение жидкости, выражаемое следующими уравнениями: x = ξ, z = ζ y = η + В(1 — ξ 2 /a 2 )t. Жидкость течет между двумя стенками, параллельными плоскости yz и отстоящими от нее на расстоянии а по обе стороны ее; все точки движутся прямолинейно параллельно оси у-ов со скоростями постоянными и тем большими, чем точки ближе к средней плоскости yz. При этой Д. все точки жидкости, находившиеся в момент t = 0 в плоскости, перпендикулярной к оси у-ов, в момент t будут находиться на параболическом цилиндре, между тем как при однородной Д. всякая плоскость остается плоскостью. Д. Б. Деформация тела под влиянием действующих на него внешних сил служит основанием современной теории строительной механики, с помощью которой вычисляется сопротивление материалов и определяются напряжения частей сложных сооружений, а следовательно, и потребные их размеры. При этом принцип производной работы Д. применяется для определения перемещения точек упругих систем. Всякое твердое тело рассматривается как система материальных точек, связанных между собой частичными, внутренними силами. Из внешних сил, могущих действовать на тело, рассматриваются сопротивления опор и разного рода нагрузки, приложенные в точках поверхности тела, и сила тяжести и другие подобные силы, действующие на частицы его массы независимо от поверхности. Всякая внешняя сила производит Д. тела, которая по удалении силы более или менее исчезает. Внутренние силы, стремящиеся восстановить первоначальную форму тела, измененную внешними силами, называются силами упругости. Та часть видоизменения тела, которая исчезает по прекращении действия внешних сил, называется упругим, а остальная часть — остающимся, или постоянным видоизменением. В обычных теоретических выводах строительной механики рассматриваются условия равновесия внутренних сил упругости с внешними силами только до тех пределов этих сил, при которых постоянных видоизменений вовсе не происходит или, во всяком случае, такие видоизменения не замечаются. Теория сопротивления материалов рассматривает только твердые тела, изменения которых под действием внешних сил имеют место по отношению как объема их, так и самого вида тел (в жидких телах изменяется только вид тела). Если внешние силы, действующие на тело, возрастают от нуля постепенно, то и изменение формы тела увеличивается мало-помалу. В случае внезапного приложения или отнятия силы, а также в случае не вполне постепенного изменения сил, тело испытывает колебания или качания около формы покоя, амплитуда которых постепенно уменьшается, пока тело наконец не примет окончательной формы равновесия. Сила упругости, проявляющаяся при Д. тела, всегда противоположна направлению перемещения частиц. Внутренние силы исполняют при видоизменении, произведенном внешними силами, отрицательную работу. Сумма работ всех этих сил и есть совокупная работа деформации, равная по величине и обратная по знаку работе внешних сил, а при неподвижных опорах — работе нагрузки. В зависимости от рода действия внешних сил, внутренние силы сопротивления могут быть растягивающие (см. Растяжение), сжимающие (см. Сжатие) и скалывающие (см. Скалывание). При данной форме твердого тела, определенном числе и расположении опор и данных по величине, направлениям и точкам приложения внешних сил (нагрузок) напряжения в частях тела определяются, на основании теории упругости, из условия равенства работы внутренних сил сопротивления при Д. тела работе внешних сил (см. Изгиб). Этим же принципом пользуются для расчета сложных систем (сочлененных), для чего с удобством можно пользоваться началом производной работы Д. А. Т.

ДЕФОРМАЦИЯ

деформация: Искажение формы куска мыла по сравнению с предусмотренной в техническом документе. Источник: ГОСТ 28546-2002: Мыло туалетное твердое. Об. смотреть

Источник