что такое объем масса плотность
Расчет массы и объема тела по его плотности
Содержание
Сейчас нам предстоит взглянуть на эту формулу с других сторон: мы научимся находить объем и массу по известной плотности материала тела; решать задачи, используя полученные знания.
Расчет массы тела по его плотности
Знание плотности веществ очень важно для многих практических целей. Для инженеров и строителей, например, знание плотности имеет колоссальное значение – так они могут рассчитать массу будущего механизма или строения.
$$m = \rho V$$
Чтобы рассчитать массу тела, если известны его объем и плотность, нужно плотность умножить на объем.
Дано:
$\rho = 8500 \frac<кг><м^3>$
$V = 0,15 м^3$
Показать решение и ответ
Решение:
$m = \rho \cdot V$
$m = 8500 \frac<кг> <м^3>\cdot 0,15 м^3 = 1275 кг \approx 1,3 т$
Расчет объема тела по его плотности
Подобным образом выразим из формулы плотности объем:
Чтобы рассчитать объем тела, если известны его масса и плотность, нужно массу разделить на плотность.
Данной формулой для определения объема часто пользуются в тех случаях, когда тела имеют сложную неправильную форму.
Рассмотрим пример задачи на расчет объема. Молоко в бутылке имеет массу 1,03 кг. Рассчитайте объем бутылки.
Дано:
$\rho = 1030 \frac<кг><м^3>$
$m = 1,03 кг$
Дополнительные примеры задач
На рисунке изображен кусок хозяйственного мыла в упаковке. По данным производителя размеры размеры его полиэтиленовой упаковки составляют 6 см x 9 см x 5,5 см.
Вес одного куска 200 г. Вес брутто (масса товара вместе с упаковкой) указан 211 г. Найдите объем куска мыла без упаковки. Выразите ответ в СИ.
Дано:
$a = 6 см$
$b = 9 см$
$c = 5,5 см$
$m_м = 200 г$
$m = 211 г$
Показать решение и ответ
Общий объем упаковки и мыла:
$V = a \cdot b \cdot c = 6 см \cdot 9 см \cdot 5,5 см = 297 см^3$.
Общий объем куска мыла в упаковке складывается из объема самого куска и объема упаковки. Так мы можем найти объем куска мыла:
$V_м = V – V_ <уп>= 297 см^3 – 12 см^3 = 285 см^3$.
Выразим в СИ:
$285 см^3 = 285 \cdot 1 см \cdot 1 см \cdot 1 см = 285 \cdot 0,01 м \cdot 0,01 м \cdot 0,01 м = 285 \cdot 0,000001 м^3 = 0,000285 м^3$.
Проверить это достаточно просто: рассчитаем плотность этого шара:
Сравним полученное значение с табличной плотностью чугуна:
$\rho = 7 \frac<г><см^3>$
Сколько бы тогда весил сплошной шар?
$m = \rho V = 7 \frac<г> <см^3>\cdot 125 см^3 = 875 г$
Разница между массами реального и предполагаемого сплошного шара составляет 75 г.
Следовательно, реальный шар имеет внутри какую-то полость, он не полностью выполнен из чугуна.
$20 дм^3 = 20 \cdot 0,1 м \cdot 0,1 м \cdot 0,1 м = 20 \cdot 0,001 м^3 = 0,02 м^3$
Дано:
$\rho = 400 \frac<кг><м^3>$
$n = 48$
$V = 20 дм^3$
Показать решение и ответ
Решение:
Рассчитаем массу одного соснового бревна:
$m = \rho \cdot V = 400 \frac<кг> <м^3>\cdot 0,02 м^3 = 8 кг$
Масса всех сосновых бревен (M) будет равна:
$M = n \cdot m = 48 \cdot 8 кг = 384 кг$
Ответ: масса автомобиля после загрузки увеличится на 384 кг.
Расчёт массы по плотности и объёму: теория, формулы, примеры задач
Содержание:
Все замечали, что одинаковые тела, сделанные из различных материалов, обладают разной массой. В единице объёма, например, древесины, концентрируется меньший вес, чем в металле. Литровая банка гречневой крупы весит около 800 г, а воды – 1 кг. Объясним подобное явление, покажем, как проводить расчет массы тел по плотности и объему.
Теоретическая выкладка
Ещё в Древней Греции учёные знали формулу определения объема вещей в зависимости от массы и плотности. Так Архимед открыл закон, названный его именем. Почему же ведро с водой поднять заметно легче, чем с песком? Всё объясняется различной плотностью веществ. В единице объёма песка больше вещества, чем в воде, значит, он плотнее жидкой субстанции.
Структура практически всех окружающих субстанций неравномерна, а значит, и концентрация массы в единице веществ отличается, но незначительно. В задачах этой разницей пренебрегают.
Плотностью называется величина, получаемая вследствие разделения массы объекта на занимаемое им пространство. В физике имеет вид:
ρ = m/V, ρ – читается как «ро».
В физике существует несколько трактовок или типов плотностей:
Относительно к газам формула видоизменяется:
ρ = M / Vm, здесь, M и Vm – молярные масса с объёмом соответственно.
Особенности
Реальную плотность вычисляют из кажущейся (насыпной) через определённый на практике коэффициент – исключает пустоты.
С ростом температуры плотность вещества снижается, хотя есть исключения, например, вода. При 4 °C она наиболее плотная, при охлаждении и нагреве значение снижается, причём лёд легче воды в жидком состоянии.
Задачи
Воспользуемся формулой массы через её плотность и объем:
Кубические сантиметры переведём в метры: 34,8 cм 3 = 0,00348 м 3 – запятая переносится на 4 знака левее или число делится на 10 000.
m = 2400 * 0,00348 = 8,352 кг.
Вычислить вес сухого дубового бруса длиной 3 м с квадратным сечением 10 × 10 см.
Для формулы массы тела (вещества) через плотность нужно высчитать объём бруса – параллелепипеда.
ρ дуба зависит от его влажности, сухим принято считать пиломатериал с влажностью ниже 20%. Из таблицы ρ равняется не более 720 кг/м3.
Упростим формулу: m = S * l * ρ = a * a * l * ρ = a 2 * l * ρ.
Подставляем значения: m = 0,1 2 * 3 * 720 = 21,6 кг.
Использование формулы массы через плотность и объём
Прежде, чем приступить к изучению формул массы, плотности и объёма, следует уточнить некоторые детали:
Формула и удивительная история её возникновения
Самое интересное – это то, что формулу нашёл мужик, который бегал голышом по улице и был при этом другом царя. Интересно? Тогда следующие три абзаца для вас.
Был в Древней Греции такой царь-тиран, как Гиерон II. Он начал подозревать, что его корону сделали не из чистого золота и ювелиры его облапошили. Но Гиерон не знал, как можно это доказать. Тогда он обратился к умнейшему человеку того времени – Архимеду. Получив приказ разобраться с делами государственной важности, Архимед день за днём стал искать решение вопроса.
Ох, и нелёгкая же задачка выпала учёному. Ведь на то время не было ни нужных формул, ни современных девайсов, ни гугла, чтобы быстренько найти решение. И вот однажды, придя в баню и погрузившись в неё, Архимед заметил, что выливающаяся вода равна по объёму тому, что погружено в воду.
Эврика! – Прокричал Архимед и нагишом поспешил в свою лабораторию проводить опыты. Учёный сложил все данные в своей голове и позже проделал следующий опыт: он взял корону и опустил её в воду. Затем он взял кусок золота такого же веса и опустил его также в воду. Объём вытесненной воды получился разным. Если бы корона была сделана из чистого золота, то её объём и слитка совпали. Это доказывало то, что ювелиры обманули царя. Кто бы мог подумать, что одно из величайших открытий появилось благодаря обманщикам, тирану и учёному.
Обозначения и термины
Далее будет приведён список понятий и их определение в условиях понятий об измерениях плотности:
Примеры решения задач
Прежде чем приступить к примерам, следует понимать, что если данные даны в килограммах и кубических сантиметрах, то нужно либо сантиметры перевести в метры, либо килограммы перевести в граммы. По такому же принципу надо переводить и остальные данные – миллиметры, тонны и так далее.
Задача 1. Найти массу тела, состоящего из вещества, плотность которого равна 2350 кг/м³ и имеет объём 20 м³. Применяем стандартную формулу и с лёгкостью находим значение. m = p*V= 2 350 * 20 = 47 000 кг.
Задача 2. Уже известно, что плотность чистого золота без примесей равна 19,32 г/см³. Найти массу драгоценной цепочки из золота, если объём составляет 3,7 см³. Воспользуемся формулой и подставим значения. p = m / V = 19,32/3,7 = 5,22162162 гр.
Задача 3. На склад поставили металл с плотностью 9250 кг/м³. Масса составляет 1,420 тонн. Нужно найти занимаемый металлом объём. Тут нужно сначала перевести либо тонны в килограммы, либо метры в километры. Проще будет воспользоваться первым методом. V = m / p = 1420/9250 = 0.153513514 м³.
Зачем и кому нужно знать эти формулы
В любой стране есть стандарты, по которым производится продукция. Неважно, какая это отрасль – пищевая, химическая или другая. Стандарты также могут быть мировыми. Так вот для того чтобы выпускаемая на заводах продукция соответствовала этим стандартам и нужны знания о плотности, массе и объёме.
Но зачем кому-то придерживаться чьих-то правил? Для начала, эти правила взяты не с потолка. К этому пришли разные бизнесмены со всего мира и нашли оптимальное решение, удовлетворяющее как производителей, так и конечных пользователей продукта. Если бы все выпускали продукцию как им вздумается, то людям было бы очень тяжело выбрать производителя. Ведь даже сейчас, со всеми стандартами и ГОСТами выбор просто огромный.
Кроме того, игнорируя физику и математику, можно выработать продукцию себе же в убыток или сделать продукцию, которая не оправдает ожиданий и будет выглядеть не так, как задумывал производитель. Есть и другие ситуации, где необходимы знания подобного рода – при подсчёте планируемого объёма, который займёт продукция на складе; вес продукции, которую нужно будет перевести и т.д.
Эти знания могут потребоваться инженерам, технологам, конструкторам и прочим профессиям, чья деятельность связана с физическими материалами. Конечно, для простого обывателя эти знания могут и не пригодиться. Однако, стоит вспомнить про случай с Архимедом и тогда вы поймёте, что знания – защита от обмана и настоящая сила!
Видео
В видео очень подробно объясняется, как рассчитать массу и объем тела по его плотности.
Формула массы через плотность и объем является одной из базовых формул физики, изучаемых в рамках школьной программы еще в седьмом классе. Она пригодится в решении многих задач.
Формула зависимости массы от объема и плотности
Для того, чтобы найти плотность жидкости или твердого вещества, существует базовая формула: плотность равна массе, поделенной на объем.
Записывается это так:
И из нее можно вывести еще две формулы.
Формулу для объема тела:
А также формулу для расчета массы:
Как видите, запомнить последнюю очень легко: это единственная формула, где две единицы нужно умножить.
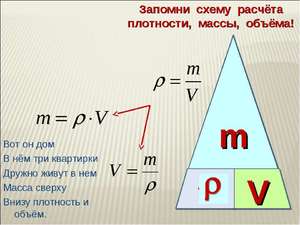
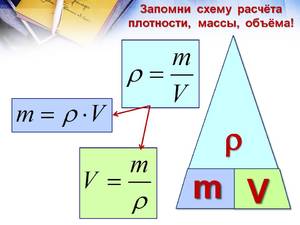
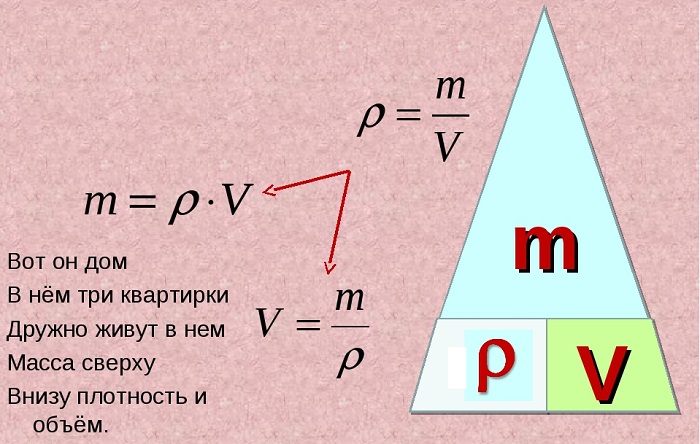
Для запоминания этой зависимости можно использовать рисунок в виде «пирамидки», разделенной на три секции, в вершине которой находится масса, а в нижних углах – плотность и объем.
Несколько иначе обстоят дела с газами. Рассчитать их вес гораздо сложнее, так как у газов нет постоянной плотности: они рассеиваются и занимают весь доступный им объем.
Для этого пригодится понятие молярной массы, которую можно найти, сложив массу всех атомов в формуле вещества при помощи данных из периодической таблицы.
Вторая единица, которая нам понадобится – количество вещества в молях. Его можно вычислить по уравнению реакции. Подробнее об этом можно узнать в рамках курса химии.
Другой способ нахождения мольного количества – через объем газа, который нужно поделить на 22,4 литра. Последнее число – это объемная постоянная, которую стоит запомнить.
В итоге, зная две предыдущие величины, мы можем определить массу газа:
где M – это молярная масса, а n – количество вещества.
Результат получится в граммах, поэтому для решения физических задач важно не забыть перевести его в килограммы, поделив на 1000. Числа в этой формуле часто могут оказываться достаточно сложными, поэтому для вычислений может понадобиться калькулятор.
Еще один нестандартный случай, с которым можно столкнуться – необходимость найти плотность раствора. Для этого существует формула средней плотности, построенная аналогично формулам других средних величин.
Для двух веществ посчитать ее можно так:
Также из этой формулы можно вывести несколько других в зависимости от того, какие из величин известны по условию задачи.
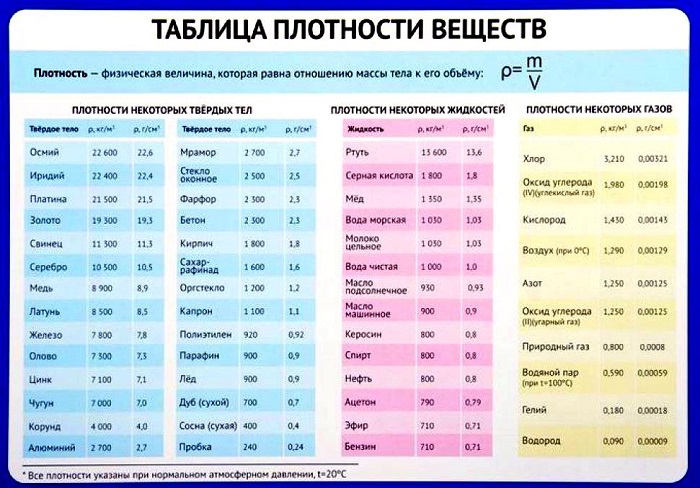
Таблица плотности некоторых веществ
Плотность многих веществ известна заранее и легко находится по соответствующей таблице.
В работе с ней важно обращать внимание на размерности и не забывать о том, что все данные собраны при нормальных условиях: комнатной температуре в 20 градусов Цельсия, а также определенном давлении, влажности воздуха и так далее.
Плотности других, более редких веществ можно найти онлайн.
Как минимум одно из значений плотности стоит запомнить, так как оно часто появляется в задачах. Это плотность воды – 1000 кг/м3 или 1 г/см3.
Примеры решения задач
Задача 1
Условие: имеется алюминиевый брусок со сторонами 3, 5 и 7 сантиметров. Какова его масса?
Найдем объем бруска:
V = 3 * 5 * 7 = 105 см 3 ;
Табличное значение плотности алюминия: 2800 кг/м 3 или 2,8 г/см 3 ;
Вычислим массу бруска:
Задача 2
Задача по смежной теме.
Условие: сколько энергии потребуется для того, чтобы довести воду комнатной температуры (20 градусов Цельсия) из стакана (ёмкость 200 мл) до температуры кипения?
m = 200 * 1 = 200 г = 0,2 кг;
Q = 4200 * 0,2 * (100 – 20) = 67200 Дж = 67,2 кДж.
Задача 3
Задача с молярной массой.
Условие: найдите массу CO2 при объеме в 5,6 л.
Найдем молярную массу CO2 :
M = 12 + 16 * 2 = 44 г/моль;
Найдем количество вещества через объем:
n = 5,6 / 22,4 = 0,25 моль;
Формула массы через плотность и объем — примеры вычислений
Формула массы через плотность и объем является одной из базовых формул физики, изучаемых в рамках школьной программы еще в седьмом классе. Она пригодится в решении многих задач.
Формула зависимости массы от объема и плотности
Для того, чтобы найти плотность жидкости или твердого вещества, существует базовая формула: плотность равна массе, поделенной на объем.
Записывается это так:
И из нее можно вывести еще две формулы.
Формулу для объема тела:
А также формулу для расчета массы:
Как видите, запомнить последнюю очень легко: это единственная формула, где две единицы нужно умножить.
Для запоминания этой зависимости можно использовать рисунок в виде «пирамидки», разделенной на три секции, в вершине которой находится масса, а в нижних углах – плотность и объем.
Несколько иначе обстоят дела с газами. Рассчитать их вес гораздо сложнее, так как у газов нет постоянной плотности: они рассеиваются и занимают весь доступный им объем.
Для этого пригодится понятие молярной массы, которую можно найти, сложив массу всех атомов в формуле вещества при помощи данных из периодической таблицы.
Вторая единица, которая нам понадобится – количество вещества в молях. Его можно вычислить по уравнению реакции. Подробнее об этом можно узнать в рамках курса химии.
Другой способ нахождения мольного количества – через объем газа, который нужно поделить на 22,4 литра. Последнее число – это объемная постоянная, которую стоит запомнить.
В итоге, зная две предыдущие величины, мы можем определить массу газа:
где M – это молярная масса, а n – количество вещества.
Результат получится в граммах, поэтому для решения физических задач важно не забыть перевести его в килограммы, поделив на 1000. Числа в этой формуле часто могут оказываться достаточно сложными, поэтому для вычислений может понадобиться калькулятор.
Еще один нестандартный случай, с которым можно столкнуться – необходимость найти плотность раствора. Для этого существует формула средней плотности, построенная аналогично формулам других средних величин.
Для двух веществ посчитать ее можно так:
Также из этой формулы можно вывести несколько других в зависимости от того, какие из величин известны по условию задачи.
Таблица плотности некоторых веществ
Плотность многих веществ известна заранее и легко находится по соответствующей таблице.
В работе с ней важно обращать внимание на размерности и не забывать о том, что все данные собраны при нормальных условиях: комнатной температуре в 20 градусов Цельсия, а также определенном давлении, влажности воздуха и так далее.
Плотности других, более редких веществ можно найти онлайн.
Как минимум одно из значений плотности стоит запомнить, так как оно часто появляется в задачах. Это плотность воды – 1000 кг/м3 или 1 г/см3.
Примеры решения задач
Задача 1
Условие: имеется алюминиевый брусок со сторонами 3, 5 и 7 сантиметров. Какова его масса?
Найдем объем бруска:
V = 3 * 5 * 7 = 105 см 3 ;
Табличное значение плотности алюминия: 2800 кг/м 3 или 2,8 г/см 3 ;
Вычислим массу бруска:
Задача 2
Задача по смежной теме.
Условие: сколько энергии потребуется для того, чтобы довести воду комнатной температуры (20 градусов Цельсия) из стакана (ёмкость 200 мл) до температуры кипения?
m = 200 * 1 = 200 г = 0,2 кг;
Q = 4200 * 0,2 * (100 – 20) = 67200 Дж = 67,2 кДж.
Задача 3
Задача с молярной массой.
Условие: найдите массу CO2 при объеме в 5,6 л.
Найдем молярную массу CO2 :
M = 12 + 16 * 2 = 44 г/моль;
Найдем количество вещества через объем:
n = 5,6 / 22,4 = 0,25 моль;