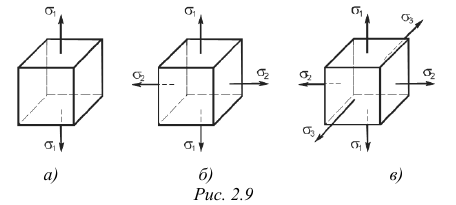
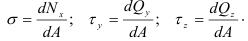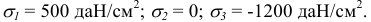что такое нормальное напряжение в технической механике

Понятие о механических напряжениях. Нормальные напряжения

Механическое напряжение — это мера внутренних сил, возникающих в деформируемом теле под влиянием различных факторов. Механическое напряжение в точке тела определяется как отношение внутренней силы к единице площади в данной точке рассматриваемого сечения.

Напряжения являются результатом взаимодействия частиц тела при его нагружении. Внешние силы стремятся изменить взаимное расположение частиц, а возникающие при этом напряжения препятствуют смещению частиц, ограничивая его в большинстве случаев некоторой малой величиной.

Q — механическое напряжение.

F — сила, возникшая в теле при деформации.

Различают две составляющие вектора механического напряжения:

Нормальное механическое напряжение — приложено на единичную площадку сечения, по нормали к сечению (обозначается σ).

Нормальное напряжение — отношение составляющей силы, действующей перпендикулярно данному сечению, к площади этого сечения. Измеряется в кг/мм 2 или кг/см 2 ;

в зависимости от знака различают сжимающие и растягивающие нормальные напряжения. Последние играют решающую роль в процессах хрупкого разрушения. Если на площадках действуют только нормальные напряжения (без касательных), то объемное (трехосное) напряженное состояние может быть охарактеризовано тремя величинами, напр. в цилиндрическом стержне — осевым, окружным и радиальным нормальным напряжением.

Понятие о схемах главных нормальных напряжениях.

Главными называют нормальные напряжения на площадках выделенного элемента с нулевыми касательными напряжениями.

Для любого случая нагружения бруса всегда можно найти такое положение мысленно выделенного в нем элемента, на гранях которого касательные напряжения будут отсутствовать (т.е. τ=0)

Площадки (грани элемента) на которых касательные напряжения равны нулю называются главными.

Таким образом, главные – это нормальные напряжения на главных площадках.

Обозначение главных напряжений

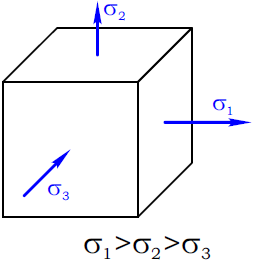
Главные напряжения принято обозначать буквой σ с индексом 1, 2 и 3.

При этом наибольшее, с учетом знака, напряжение обозначается как σ1 а наименьшее соответственно σ3.

Другими словами, главное напряжение, расположенное на числовой оси правее других – σ1, а то, которое левее всех σ3.

Например, для случая объемного напряженного состояния:

При плоском напряженном состоянии:

1. Когда оба напряжения растягивающие

2. По одной грани напряжение растягивающее, по другой сжимающее

3. Оба напряжения сжимающие.

При линейном напряженном состоянии единственное напряжение всегда обозначается как σ1 или просто σ.

Дата добавления: 2018-05-12 ; просмотров: 2098 ; Мы поможем в написании вашей работы!

Источник

Понятие о напряжениях

Понятие о напряжениях

Напряженное состояние в точке

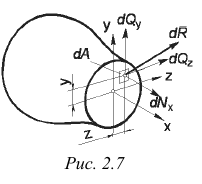
Внутренние усилия, которые были найдены выше из уравнений статики, не являются реальными, а представляют собой лишь статический эквивалент этих усилий, распределенных по всей площади рассматриваемого сечения. Иначе говоря, найденные усилия являются равнодействующими действительных внутренних сил, возникающих в каждой точке сечения. В сечении части А (рис. 2.6, б) выделим элементарную площадку 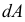(рис. 2.7).

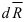
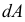
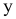
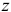
В силу малости элемента можно считать, что внутренние усилия, приложенные к его различным точкам, одинаковы по величине и направлению. Тогда равнодействующая их будет проходить через центр тяжести площади элемента , координаты которого равны и .

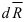
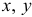
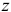
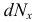
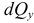
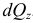
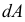
Проектируя вектор на оси и , получим элементарную продольную силу и элементарные поперечные силы и . Разделив эти усилия на площадь , получим величины внутренних сил, приходящихся на единицу площади, рис. 2.7:

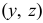
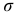
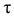
Эти величины называют напряжениями в точке поперечного сечения тела, причем — нормальное напряжение; — касательное напряжение.

Нормальные и касательные напряжения

Нормальные и касательные напряжения представляют собой интенсивность распределения соответственно нормальных и поперечных сил, действующих по элементарной площадке в рассматриваемой точке.

Через любую точку упругого тела, подверженного действию внешней нагрузки, можно провести бесчисленное множество сечений (площадок), по которым в общем случае будут действовать как нормальные, так и касательные напряжения. При этом величина и направление указанных напряжений в каждом конкретном случае будут зависеть от ориентации площадки.

Деформация нагруженного тела сопровождается изменением расстояний между его частицами. Внутренние силы, возникающие между частицами, изменяются под действием внешней нагрузки до тех пор, пока не установится равновесие между внешней нагрузкой и внутренними силами сопротивления. Полученное состояние тела называют напряженным состоянием. Оно характеризуется совокупностью нормальных и касательных напряжений, действующих по всем площадкам, которые можно провести через рассматриваемую точку. Исследовать напряженное состояние в точке тела — значит получить зависимости, позволяющие определить напряжения по любой площадке, проходящей через указанную точку.

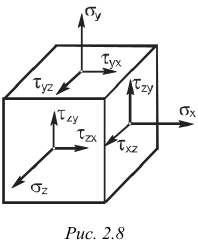
Для исследования напряженного состояния в окрестности исследуемой точки тела обычно выделяют элемент в виде бесконечно малого параллелепипеда (рис. 2.8). На его гранях действуют внутренние силы, заменяющие воздействие удаленной части тела и вызывающие появление напряжений. Полные напряжения на гранях можно разложить на нормальные и касательные составляющие. Если ориентацию выделенного элемента изменить, то действующие на его гранях напряжения будут также изменяться. При этом можно найти такое положение элемента, при котором на его гранях касательные напряжения равны нулю.

Грани элемента, по которым касательные напряжения не действуют, называют главными площадками, а нормальные напряжения на них — главными напряжениями.

Доказано, что в каждой точке тела имеются по крайней мере три главные площадки, причем они всегда взаимно перпендикулярны.

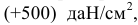
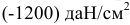
Следовательно, в каждой точке будут также три главных напряжения, линии действия которых определяют три главных направления напряженного состояния в данной точке. Главные напряжения принято обозначать так, чтобы наибольшее из них (в алгебраическом смысле) имело индекс 1, а наименьшее — индекс 3. Например, если одно из главных напряжений равно нулю, другое , а третье — , то

В зависимости от величины главных напряжений различают следующие виды напряженного состояния в точке: линейное, или одноосное — только одно главное напряжение (любое из трех) отлично от нуля, а два других равны нулю (рис. 2.9, а); плоское, или двухосное — два главных напряжения отличны от нуля (рис. 2.9, б); объемное, или трехосное — все главные напряжения отличны от нуля (рис. 2.9, в).

На практике чаще всего имеют место два первых вида напряженного состояния.

Эта теория взята со страницы лекций по предмету «прикладная механика»:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Механическое напряжение

Механика сплошных сред

Сплошная среда

Классическая механика Закон сохранения массы · Закон сохранения импульса Теория упругости Напряжение · Тензор · Твёрдые тела · Упругость · Пластичность · Закон Гука · Реология · Вязкоупругость Гидродинамика Жидкость · Гидростатика · Гидродинамика · Вязкость · Ньютоновская жидкость · Неньютоновская жидкость · Поверхностное натяжение Основные уравнения Уравнение непрерывности · Уравнение Эйлера · Уравнения Навье — Стокса · Уравнение диффузии · Закон Гука Известные учёные Ньютон · Гук Бернулли · Эйлер · Коши · Стокс · Навье

См. также: Портал:Физика

Механическое напряжение — это мера внутренних сил, возникающих в деформируемом теле под влиянием различных факторов. Механическое напряжение в точке тела определяется как отношение внутренней силы к единице площади в данной точке рассматриваемого сечения.

Напряжения являются результатом взаимодействия частиц тела при его нагружении. Внешние силы стремятся изменить взаимное расположение частиц, а возникающие при этом напряжения препятствуют смещению частиц, ограничивая его в большинстве случаев некоторой малой величиной.

Q — механическое напряжение. F — сила, возникшая в теле при деформации. S — площадь.

Различают две составляющие вектора механического напряжения:

Совокупность напряжений, действующих по различным площадкам, проведенным через данную точку, называется напряженным состоянием в точке.

В системе СИ механическое напряжение измеряется в паскалях.

Тензор механического напряжения

Здесь под понимаются компоненты вектора, образованного из нормали к элементарной площадке и её площади :

Таким образом сила, действующая на некий объём V равна интегралу тензора напряжения на границе этого объёма по поверхности этого объёма (в отсутствие объёмных сил):

См. также

Полезное

Смотреть что такое «Механическое напряжение» в других словарях:

механическое напряжение — деформация напряженное состояние воздействие — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы деформациянапряженное состояниевоздействие EN… … Справочник технического переводчика

механическое напряжение — įtempis statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, susijęs su vidinėmis jėgomis, atsirandančiomis išorinių jėgų veikiamoje medžiagoje. Jis išreiškiamas veikiančios jėgos ir ploto, į kurį veikia jėga, dalmeniu. atitikmenys … Penkiakalbis aiškinamasis metrologijos terminų žodynas

механическое напряжение — įtempis statusas T sritis fizika atitikmenys: angl. stress vok. Beanspruchung, f; Spannung, f rus. механическое напряжение, n; напряжение, n pranc. contrainte, f; contrainte mécanique, f … Fizikos terminų žodynas

механическое напряжение — įtempis statusas T sritis Energetika apibrėžtis Vidinių jėgų, atsiradusių dėl išorinių poveikių, intensyvumas kūno taške, plote, erdvėje. Jis išreiškiamas veikiančios jėgos ir ploto, į kurį veikia jėga, dalmeniu. atitikmenys: angl. stress vok.… … Aiškinamasis šiluminės ir branduolinės technikos terminų žodynas

механическое напряжение — mechaninis įtempis statusas T sritis chemija apibrėžtis Vidinės jėgos, atsirandančios išorinių jėgų veikiamoje medžiagoje. atitikmenys: angl. mechanical stress rus. механическое напряжение … Chemijos terminų aiškinamasis žodynas

механическое напряжение — mechaninis įtempis statusas T sritis fizika atitikmenys: angl. mechanical stress vok. mechanische Biegespannung, f rus. механическое напряжение, n pranc. contrainte mécanique, f … Fizikos terminų žodynas

механическое напряжение, приводящее к отказу (оборудования) — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN stress to failureSTOF … Справочник технического переводчика

Касательное механическое напряжение — Механика сплошных сред Сплошная среда Классическая механика Закон сохранения массы · Закон сохранения импульса … Википедия

Нормальное механическое напряжение — Механика сплошных сред Сплошная среда Классическая механика Закон сохранения массы · Закон сохранения импульса … Википедия

Источник

iSopromat.ru

Определения видов механических напряжений при расчете элементов конструкций и их перевод на английский язык.

78. Напряжение
Stress
Интенсивность внутренних сил в определенной точке данного сечения.

79. Нормальное напряжение
Normal stress
Составляющая напряжений, направленных по нормали к площадке ее действия.

80. Касательное напряжение
Shearing stress
Составляющая напряжений, лежащих в плоскости сечения.

81. Переменное напряжение
Alternate stress
Напряжения, переменные во времени, возникающие в элементах конструкции под действием нагрузок, переменных по величине или направлению, а также нагрузок, перемещающихся относительно рассматриваемого элемента.

82. Допускаемое напряжение
Allowable stress
Экспериментально установленное для рассматриваемого материала предельное значение напряжения, деленное на коэффициент запаса прочности.

83. Главное напряжение
Principal stress
Среди множества площадок, которые можно провести через исследуемую точку, имеются три взаимно перпендикулярные площадки, касательные напряжения на которых отсутствуют. Эти площадки и возникающие на них нормальные напряжения называются главными.

84. Эквивалентное (приведенное) напряжение
Equivalent stress
Напряжение одноосного растяжения (сжатия), равноопасного рассматриваемому сложному напряженному состоянию.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Тема 2.2. Растяжение и сжатие

Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы N, а прочие силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю.

Это самый простой и часто встречающийся вид деформации. Обычно он наблюдается когда внешняя нагрузка действует вдоль продольной оси стержня. Продольной осью стержня называется линия, проходящая через центры тяжести поперечных сечений.

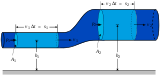
Обычным является растяжение стержня силами, приложенными к его концам. Передача усилий к стержню может быть осуществлена различными способами, как это показано на рис. 1.

Рис. 1. Растяжение стержня

Во всех случаях, однако, система внешних сил образует равнодействующую F, направленную вдоль оси стержня. Поэтому независимо от условий крепления растянутого стержня, расчетная схема в рассматриваемых случаях (рис. 1, а, б) оказывается единой (рис. 1, в) согласно принципу Сен – Венана.

Если воспользоваться методом сечений (рис. 2), то становится очевидным, что во всех поперечных сечениях стержня возникают нормальные силы N_z, равные силе F (рис. 2, б).

Сжатие отличается от растяжения, формально говоря, только знаком силы N_z. При растяжении нормальная сила N_z направлена от сечения (рис. 2, б), а при сжатии – к сечению.

Рис. 2. Нормальная сила N

Растягивающие продольные силы принято считать положительными (рис. 3, а), а сжимающие – отрицательными (рис. 3, б).

Рис. 3. Знак продольной силы N

При расчете стержней, испытывающий деформацию растяжения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от N_z), возникающих в стержне, и нахождение линейных перемещений в зависимости от внешней нагрузки.

Продольные силы (N_z), возникающие в поперечных сечениях стержня, определяются по внешней нагрузке с помощью метода сечений.

График, показывающий изменение продольных сил по длине оси стержня, называется эпюрой продольных сил (эп. N_z). Он дает наглядное представление о законе изменения продольной силы.

Осью абсцисс служит ось стержня. Каждая ордината графика – продольная сила (в масштабе сил) в данном сечении стержня.

Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти N_max при растяжении-сжатии). Сечение, где действует максимальное усилие будем называть опасным.

Перед построением эпюр необходимо освободить брус, в котором будем строить эпюры от опорных связей (выделить объект равновесия) и приложить к нему все действующие внешние силы (активные и реактивные). Затем необходимо установить границы участков, в пределах которых закон изменения внутренних сил постоянный. Границами таких участков являются сечения, где приложены сосредоточенные силы или начинается и кончается распределенная нагрузка, а также сечения, где имеется перелом стержня.

Применяя метод сечений и учитывая правила знаков изложенные выше, получаем уравнения изменения внутренних сил в пределах длины каждого участка бруса. Затем, используя, полученные зависимости строим графики (эпюры) этих усилий. Ординаты эпюр в определенном масштабе откладываем от базисной линии, которую проводим параллельно оси бруса.

На основании метода сечений продольная сила в произвольном поперечном сечении стержня численно равна алгебраической сумме проекций внешних сил, приложенных к стержню по одну сторону от рассматриваемого сечения, на его продольную ось.

Причем проекция внешней силы берется со знаком плюс, если сила растягивает часть стержня от точки ее приложения до рассматриваемого сечения и, наоборот, со знаком минус – если сжимает.

§2. Напряжение в поперечных сечениях стержня

Продольная сила N с помощью метода сечений всегда может быть выражена через внешние силы. В формулe следует подставлять алгебраическое значение N т.е со знаком плюс в случае растяжения и со знаком минус в случае сжатия

§3. Расчеты на прочность и жесткость при растяжении-сжатии

Прочность стержня при осевом растяжении и сжатии обеспечена, если для каждого его поперечного сечения наибольшее расчетное (рабочее) напряжение σ не превосходит допускаемого [σ] : σ=N/A≤ [σ],

Данное выражение определяет условие прочности при растяжении или сжатии.

С помощью этой формулы решается три вида зада (выполняется три вида расчета):

1. Проверка прочности (проверочный расчет). При заданных продольной силы N и площади поперечного сечения А определяют рабочее (расчетное) напряжение и сравнивают его с допускаемым [σ].

В случаях, когда рабочее напряжения значительно ниже допускаемых σ

Источник