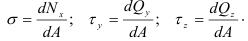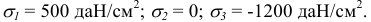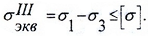что такое нормальное напряжение касательное напряжение

Понятие о напряжениях

Понятие о напряжениях

Напряженное состояние в точке

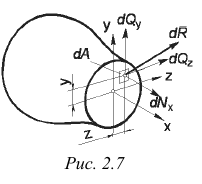
Внутренние усилия, которые были найдены выше из уравнений статики, не являются реальными, а представляют собой лишь статический эквивалент этих усилий, распределенных по всей площади рассматриваемого сечения. Иначе говоря, найденные усилия являются равнодействующими действительных внутренних сил, возникающих в каждой точке сечения. В сечении части А (рис. 2.6, б) выделим элементарную площадку 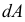(рис. 2.7).

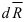
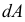
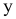
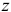
В силу малости элемента можно считать, что внутренние усилия, приложенные к его различным точкам, одинаковы по величине и направлению. Тогда равнодействующая их будет проходить через центр тяжести площади элемента , координаты которого равны и .

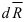
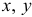
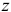
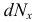
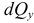
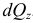
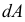
Проектируя вектор на оси и , получим элементарную продольную силу и элементарные поперечные силы и . Разделив эти усилия на площадь , получим величины внутренних сил, приходящихся на единицу площади, рис. 2.7:

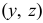
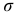
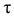
Эти величины называют напряжениями в точке поперечного сечения тела, причем — нормальное напряжение; — касательное напряжение.

Нормальные и касательные напряжения

Нормальные и касательные напряжения представляют собой интенсивность распределения соответственно нормальных и поперечных сил, действующих по элементарной площадке в рассматриваемой точке.

Через любую точку упругого тела, подверженного действию внешней нагрузки, можно провести бесчисленное множество сечений (площадок), по которым в общем случае будут действовать как нормальные, так и касательные напряжения. При этом величина и направление указанных напряжений в каждом конкретном случае будут зависеть от ориентации площадки.

Деформация нагруженного тела сопровождается изменением расстояний между его частицами. Внутренние силы, возникающие между частицами, изменяются под действием внешней нагрузки до тех пор, пока не установится равновесие между внешней нагрузкой и внутренними силами сопротивления. Полученное состояние тела называют напряженным состоянием. Оно характеризуется совокупностью нормальных и касательных напряжений, действующих по всем площадкам, которые можно провести через рассматриваемую точку. Исследовать напряженное состояние в точке тела — значит получить зависимости, позволяющие определить напряжения по любой площадке, проходящей через указанную точку.

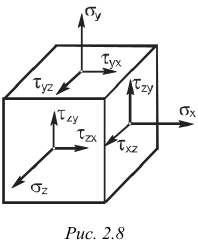
Для исследования напряженного состояния в окрестности исследуемой точки тела обычно выделяют элемент в виде бесконечно малого параллелепипеда (рис. 2.8). На его гранях действуют внутренние силы, заменяющие воздействие удаленной части тела и вызывающие появление напряжений. Полные напряжения на гранях можно разложить на нормальные и касательные составляющие. Если ориентацию выделенного элемента изменить, то действующие на его гранях напряжения будут также изменяться. При этом можно найти такое положение элемента, при котором на его гранях касательные напряжения равны нулю.

Грани элемента, по которым касательные напряжения не действуют, называют главными площадками, а нормальные напряжения на них — главными напряжениями.

Доказано, что в каждой точке тела имеются по крайней мере три главные площадки, причем они всегда взаимно перпендикулярны.

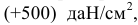
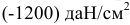
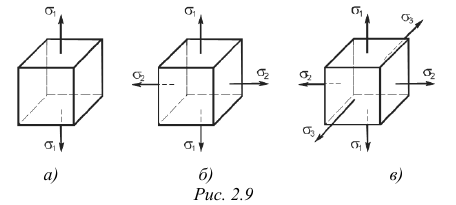
Следовательно, в каждой точке будут также три главных напряжения, линии действия которых определяют три главных направления напряженного состояния в данной точке. Главные напряжения принято обозначать так, чтобы наибольшее из них (в алгебраическом смысле) имело индекс 1, а наименьшее — индекс 3. Например, если одно из главных напряжений равно нулю, другое , а третье — , то

В зависимости от величины главных напряжений различают следующие виды напряженного состояния в точке: линейное, или одноосное — только одно главное напряжение (любое из трех) отлично от нуля, а два других равны нулю (рис. 2.9, а); плоское, или двухосное — два главных напряжения отличны от нуля (рис. 2.9, б); объемное, или трехосное — все главные напряжения отличны от нуля (рис. 2.9, в).

На практике чаще всего имеют место два первых вида напряженного состояния.

Эта теория взята со страницы лекций по предмету «прикладная механика»:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

iSopromat.ru

Важнейшим критерием оценки прочности балок при изгибе являются напряжения.

Рассмотрим способы расчета напряжений при плоском поперечном изгибе балки

Расчет напряжений

Возникающий в поперечных сечениях при чистом прямом изгибе изгибающий момент M_x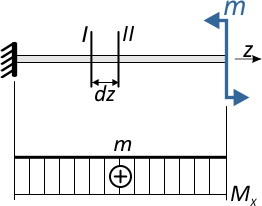

представляет собой равнодействующий момент внутренних нормальных сил, распределенных по сечению и вызывающих нормальные напряжения в точках сечения.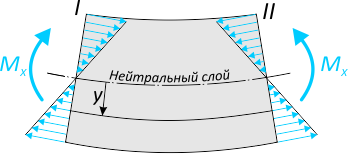

Закон распределения нормальных напряжений по высоте сечения выражается формулой: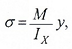

где:
M — изгибающий момент, действующий в рассматриваемом сечении относительно его нейтральной линии X;
I_x — осевой момент инерции поперечного сечения балки относительно нейтральной оси;
y – расстояние от нейтральной оси до точки, в которой определяется напряжение.

Нейтральная ось при изгибе проходит через центр тяжести поперечного сечения.

По вышеуказанной формуле, нормальные напряжения по высоте сечения изменяются по линейному закону.

Наибольшие значения имеют напряжения у верхнего и нижнего краев сечения.

Например, для симметричного относительно нейтральной оси сечения, где y₁=y₂=h/2: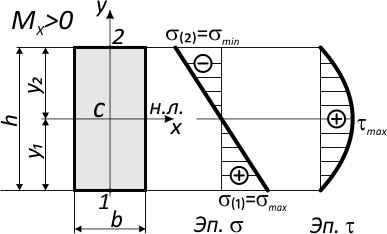

Напряжения в крайних точках по вертикали (точки 1 и 2) равны по величине, но противоположны по знаку.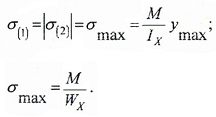

Для несимметричного сечения

напряжения определяются отдельно для нижней точки 1 и верхней точки 2: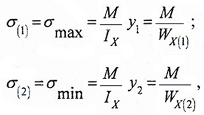

где: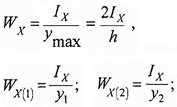

W_X — осевой момент сопротивления симметричного сечения;
W_X(1) и W_X(2) — осевые моменты сопротивления несимметричного сечения для нижних и верхних слоев балки.

Знаки нормальных напряжений при их расчете, рекомендуется определять по физическому смыслу в зависимости от того, растянуты или сжаты рассматриваемые слои балки.

Условия прочности при изгибе

Прочность по нормальным напряжениям

Условие прочности по нормальным напряжениям для балок из пластичного материала записывается в одной крайней точке.

В случае балки из хрупких материалов, которые, как известно, по-разному сопротивляются растяжению и сжатию – в двух крайних точках сечения.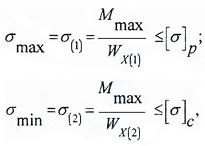

Здесь:
M_max — максимальное значение изгибающего момента, определяемого по эпюре M_x;
[ σ], [ σ]_р, [ σ]_с — допустимые значения напряжений для материала балки (для хрупких материалов – на растяжение (р) и сжатие (с)).

Для балки из хрупкого материала обычно применяют сечения, несимметричные относительно нейтральной оси. При этом сечения располагают таким образом, чтобы наиболее удаленная точка сечения размещалась в зоне сжатия, так как [ σ]_с>[ σ]_р.

В таких случаях, проверку прочности следует обязательно проводить в двух сечениях: с наибольшим положительным изгибающим моментом и с наибольшим по абсолютной величине (модулю) отрицательным значением изгибающего момента.

При расчете элементов конструкций, работающих на изгиб, с использованием вышеуказанных условий прочности решаются три типа задач:

Прочность по касательным напряжениям

В случае прямого поперечного изгиба в сечениях балки, кроме нормальных напряжений σ от изгибающего момента, возникают касательные напряжения τ от поперечной силы Q.

Закон распределения касательных напряжений по высоте сечения выражается формулой Д.И. Журавского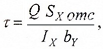

где
S_{x отс} — статический момент относительно нейтральной оси отсеченной части площади поперечного сечения балки, расположенной выше или ниже точки, в которой определяются касательные напряжения;
b_y — ширина поперечного сечения балки на уровне рассматриваемой точки, в которой рассчитывается величина касательных напряжений τ.

Условие прочности по касательным напряжениям записывается для сечения с максимальным значением поперечной силы Q_max:

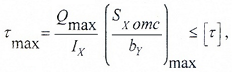
где [ τ] – допустимое значение касательных напряжений для материала балки.

Полная проверка прочности

Полную проверку прочности балки производят в следующей последовательности:

При анализе плоского напряженного состояния главные напряжения при изгибе, примут вид: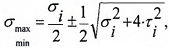

так как нормальные напряжения в поперечном направлении к оси балки принимаются равными нулю.

Проверка прочности осуществляется с помощью соответствующих гипотез прочности, например, гипотезы наибольших касательных напряжений:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Нормальные и касательные напряжения.

Единицы нормальных и касательных напряжений в СИ – паскаль (Па). Один паскаль – это напряжение, при котором на площадке в один квадратный метр возникает внутренняя сила, равная одному ньютону. Часто используют значения: 1 МПа = 10 6 Па. В технической системе единицы напряжения измеряются в килограммах силы на миллиметр в квадрате (кгс/мм 2 ).

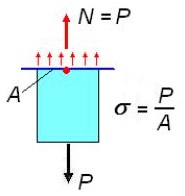
Напряжения при растяжении и сжатии.В поперечных сечениях при растяжении-сжатииимеют место только нормальные напряжения σ, которые определяются отношением внутренней силы N к площади A соответствующего поперечного сечения стержня.

Напряжения в поперечном сечении при растяжении.

Знак напряжений зависит от знака внутренней силы на рассматриваемом участке стержня. Для обеспечения необходимой прочности элементов и конструкций напряжения не должны превышать допустимых значений. При растяжении и сжатии в сечении действует только нормаль­ное напряжение. Напряжения могут рассматриваться как силы, приходящиеся на единицу площади.

Таким образом, направление и знак напряжения в сечении со­впадают с направлением и знаком силы в сечении.

Нормальное напряжение можно рассчитать по формуле:

Таким образом: величина напряжения прямо пропорциональна продольной силе и обратно пропорциональна площади поперечного сечения.

Нормальные напряжения действуют при растяжении от сечения, а при сжатии к сечению.

Размерность напряжений: Н/м 2 (Па), од­нако это слишком малая единица, и практически напряжения рас­считывают в Н/мм 2 (МПа):

Поперечные размеры стержня в результате деформирования также изменяются, при этом при растяжении они уменьшаются, а при сжатии – увеличиваются.

Источник

Понятие о напряжениях. Нормальные и касательные напряжения.

Напряжение – численная мера распределения внутренних сил по плоскости поперечного сечения. Его используют при исследовании и определении внутренних сил любой конструкции.

Выделим на плоскости сечения площадку DA; по этой площадке будет действовать внутренняя сила DR. Величина отношения DR/DA=p_ср называется средним напряжением на площадке DA. Истинное напряжение в точке А получим устремив DA к нулю

Нормальные напряжения возникают, когда частицы материала стремятся отдалиться друг от друга или, наоборот, сблизиться. Касательные напряжения связаны со сдвигом частиц по плоскости рассматриваемого сечения.

Очевидно, что . Касательное напряжение в свою очередь может быть разложено по направлениям осей x и y (τ_zх, τ_zу). Размерность напряжений – Н/м 2 (Па).

17. Понятие о напряжениях. Нормальные и касательные напряжения.

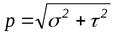
Внутренние силовые факторы. Метод сечений. Эпюры. Выражение внутренних силовых факторов через нормальные и касательные напряжения.

Внутренние силовые факторы

В процессе деформации бруса, под нагрузкой происходит изменение взаимного расположения элементарных частиц тела, в результате чего в нем возникают внутренние силы.

По своей природе внутренние силы представляют собой взаимодействие частиц тела, обеспечивающее его целостность и совместность деформаций.

Чтобы численно установить величину внутренних сил пользуются методом сечений.

Метод сеченийсводится к четырем действиям:

1. Разрезают (мысленно) тело плоскостью в том месте, где нужно определить внутренние силы (рис. 7);

Рис. 7

2. Отбрасывают любую отрезанную часть тела (желательно наиболее сложную), а ее действие на оставшуюся часть заменяют внутренними силами, чтобы оставшаяся исследуемая часть находилась в равновесии (рис.8);

Рис. 8

3. Приводят систему сил к одной точке (как правило, к центру тяжести сечения) и проецируют главный вектор и главный момент системы внутренних сил на нормаль к плоскости (ось ) и главные центральные оси сечения ( и ).

Полученные силы (N, Qy, Qz) (рис. 9) и моменты (Мк, Мy, Mz) называют внутренними силовыми факторами в сечении

Рис. 9

Для внутренних силовых факторов приняты следующие названия:

—продольная или осевая сила;

и —поперечные силы;

—крутящий момент;

и —изгибающие моменты.

4. Находят внутренние силовые факторы, составляя шесть уравнений равновесия статики для рассматриваемой части рассеченного тела.

Эпю́ра (фр. epure — чертёж) — особый вид графика, показывающий распределение величины нагрузки на объект. Например, для стержня продольная ось симметрии берётся за область определения и составляются эпюры для сил, напряжений и разных деформаций в зависимости от абсциссы.

Расчёт эпюр напряжения является базовой задачей такой дисциплины, как сопротивление материалов. В частности, только при помощи эпюры возможно определить максимально допустимую нагрузку на материал.

Для построения ординаты эпюры M в каком либо сечении стержня

необходимо выполнить следующие две операции.

1. С помощью уравнения равновесия ∑M(слева)= 0 для левой отсеченной

части стержневой системы (или ∑M(справа) = 0 для правой части) подсчитать

численное значение изгибающего момента в сечении.

2. Отложить найденное численное значение в виде ординаты перпендикулярно оси стержня со стороны растянутого волокна стержня.

Численное значение изгибающего момента в сечении равно численному значению алгебраической суммы моментов всех сил,действующих на стержневую системус любой одной из сторон сечения, взятых относительно точки на оси сечения.

Составляющую, лежащую в сечении в данной площадке обознача­ется через и называется касательным напряжением.

Нормальное напряжение, направленное от сечения, считают положительным, направленное к сечению – отрицательным.

Нормальные напряжения возникают, когда под действием внешних сил частицы, расположенные по обе стороны от сечения, стремятся удалиться одна от другой или сблизиться. Касательные напряжения возникают, когда частицы стремятся сдвинуться одна относительно другой в плоскости сечения.

Касательное напряжение можно разложить по координатным осям на две составляющие и (рис. в) Первый индекс при показывает, какая ось перпендикулярна сечению, второй – параллельно какой оси действует напряжение. Если в расчетах направление касательного напряжения не имеет значения, его обозначают без индексов.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Источник