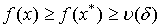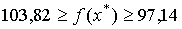что такое нормализация вектора
Управляющие силы призваны помочь автономным персонажам двигаться в реалистичной манере, с помощью использования простых сил, можно добиться, реалистичного поведения, такого как импровизационная навигация (рыскание) персонажей. В этй статье объясняется теория лежащая в основе идеи управляющих сил, обеспечивающих поведение рыскания, а также его реализацию.
Идеи, лежащие в основе управляющих сил были предложены Craig W. Reynolds; они не используют сложные стратегии, связанные с поиском пути, или глобальными вычислениями, вместо этого используется локальная информация, например, векторы соседних сущностей. Это делает идею управляющих сил простой для понимания и реализации, но все еще способной производить очень сложные модели движения.
Для понимания данной статьи необходимо понимание некоторых математических действий над векторами, я опишу их функциями на javascript в контексте 2-х мерных векторов.
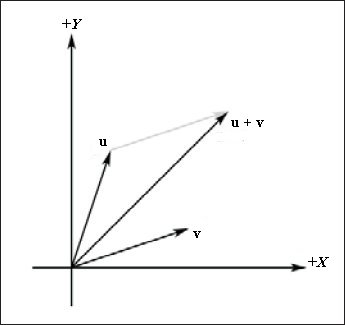
Сложение векторов
Для сложения векторов v1 и v2 необходимо выполнить покомпонентное их сложение. В результате сложения векторов получаем вектор:
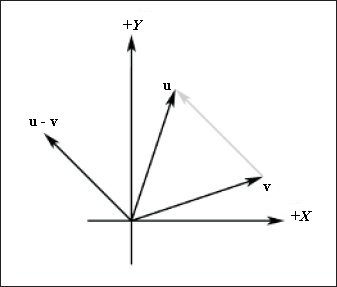
Вычитание векторов
Для вычитания векторов v1 и v2 необходимо выполнить покомпонентное их вычитание. В результате вычитания векторов получаем вектор:
Нормализация вектора (приведение к единичному вектору)
Длина вектора
Получается по теореме Пифагора: квадрат гипотинузы равен сумме квадратов катетов В результате получаем скалярное число:
Масштабирование вектора (умножение/деление на скаляр)
При умножении/делении вектора на скаляр изменяется длина вектора, но не его направление. При этом число может называться коэффициентом масштабирования. Умножение вектора на скаляр так же сводится к умножению каждого компонента вектора на скаляр. В результате умножения вектора на скаляр получаем вектор:
при делении вектора на скаляр все то же самое, но применяем соответственно операцию деления. В результате деления вектора на скаляр получаем вектор:
Скалярное произведение 2-х векторов
-Не путать с умножением на скаляр! Скалярное произведение 2-х векторов это сумма произведений компонент векторов поэтому иногда эту операцию называют внутренним произведением (inner product). В результате получаем скалярное число:
Скалярное произведение ортогональных (перпендикулярных) векторов всегда = 0! Этот факт можно удобно использовать: если скалярное произведение двух векторов = 0, то векторы ортогональны пример:
Проекция вектора на вектор
Скалярное умножение вектора на единичный вектор называется проецированием. Проецирование выделяет компонент вектора, направленный параллельно единичному вектору. Вообще проецировать можно и на не единичный вектор, но в процессе проецирования вектор на который производится проецирование один хрен нужно нормализоввывать. В результате получаем скалярное число:
Усечение вектора
Иногда бывает полезно ограничить величину вектора, например задать максимальный порог скорости или ускорения, но вектор при этом должен сохранить свое направление. Функция truncate позволяет это сделать. В результате получаем вектор:
Положение, скорость и движение.
При реализации управляющих сил мы воздействуюем на персонаж посредством математических манипуляций с его векторами (позиция,скорость и т.п.). Так как эти силы будут влиять на скорость персонажа и его положение, то использование векторов для их представления является отличной идеей.
Кстати, позиция персонажа тоже описывается вектором, в этом случае направление вектора игнорируется, важны лишь значения его компонент x и y
Направление вектора скорости будет контролировать то, куда движется персонаж, в то время, как длина вектора скорости (величина или магнитуда) будет контролировать, то как быстро он будет двигаться каждый кадр, т.е. это фактически величина шага персонажа.
Это иллюстрирует поведение «рыскания» в чистом виде, без какого-либо подруливающего поведения. Зеленая линия представляет собой вектор скорости, который вычисляется следующим образом:
Важно заметить, что без управляющего воздействия на движимые силы, персонаж описывает прямые маршруты и мгновенно меняет свое направление, когда цель движется, делая, таким образом резкие переходы. Следует заметить что данное поведение не свойственно реалистичным игровым персонажам.
Кликните мышкой на холсте, чтобы цель начала двигаться:
Расчет сил
Если в организации движения использовать только лишь скорость, тогда персонаж будет следовать по прямой линии, определяемой направлением direction вектора этой скорости. Что бы сделать поведение персонажа более реалистичным добавим дополнительные управляющие силы. В зависимости от этих сил, персонаж будет двигаться в одном или другом направлении.
Для имитации поведения поиска добавление управляющего усилия персонажу в каждом кадре заставит персонаж плавно регулировать свою скорость, избегая резких изменений маршрута. Если цель движется, персонаж будет постепенно менять свой вектор скорости, пытаясь двигаться к новомц положению цели.
Поведения поиска включает в себя две силы: желаемую скорость (desired velocity) и управляющую силу (steering):
Управляющая сила steering это результат вычитания желаемой скорости из текущей скорости. Эта сила также толкает персонажа в сторону цели.
Описанные силы вычисляются следующим образом:
Добавление сил
После того, как просчитан вектор управляющей силы, он должен быть добавлен к вектору скорости персонажа. Добавление вектора управляющей силы к вектору скорости персонажа каждый кадр заставит персонаж плавно отклоняться от прямолинейного маршрута и направиться к цели, описывая дугу seek path (оранжевая кривая на рисунке ниже):
Добавление этих сил и вычисления конечных векторов скорости и положения:
Тут мы ограничиваем управляющую силу, чтобы гарантировать что результирующая скорость не будет превышать разрешенную. Кроме того, управляющая сила, делится на массу персонажа, это даст эффект различных скоростей движения для персонажей масса которых различается.
Кликните мышкой на холсте, чтобы цели начали двигаться:
Каждый раз, когда цель движется, векторы скорости разных персонажей изменяются соответствующим образом. Вектору скорости, однако, требуется некоторое время, чтобы измениться и начать снова указывать на цель. В результате получается плавое реалистичное движение.
Вывод: управляющие силы отлично подходят для создания реалистичных моделей движения. Основная идея заключается в том, чтобы использовать локальную информацию для расчета и примененять дополнительные силы для имитации различных моделей поведения. Даже при том, что расчет прост в реализации, он вполне в состоянии производить очень сложные результаты.
Не сложно заметить, что объект с большей массой более неповоротлив чем с меньшей.
Класс sf::Vector2
Класс sf::Vector2 имеет небольшой и простой интерфейс. К его элементам x и y можно обращаться напрямую и он не содержит математических функций.
Операции с векторами
Перегруженная версия конструктора позволяет в качестве аргумента принимать другой объект этого класса:
Аналогично для копирования координаты:
Получение третьего вектора при сложение двух других:
Поскольку функции cmath работают с действительными числами, то эти координаты разумно преобразовать из целочисленных в действительные ( float ):
Но, обычно, ввиду неявного приведения типов, большой необходимости в этом нет.
Определение длины вектора (расстояний между объектами)
Нормализация вектора (единичный вектор)
В задаче, решаемой на этом уроке, нормализация используется для определения вектора направления (см. программу sf.5.1 стр. 108).
Преобразования Radians Degree
Поворот спрайта с помощью вектора направления и tan2
Символ c обозначает какая сторона (“горизонта”) будет являться точкой отсчета угла.
Разработка проекта для проверки функций
Раздельная компиляция
Код программы получился довольно громоздкий. Использовать его для продолжения разработки стало неудобным. К тому же разработанные нами функции потребуются для решения различных задач в других проектах. Поэтому мы разобьем его на несколько файлов. Как это сделать см.: §10 Функции. Раздельная компиляция. Наш проект после реорганизации будет содержать следующие файлы (исходный текст спрятан под спойлер):
Как нормализовать нулевой вектор
Предположим, у вас есть функция «нормализации», которая принимает список чисел (представляющих вектор) в качестве входных данных и возвращает нормализованный вектор. Каким должен быть результат, когда вектор равен всем нулям или сумма его компонентов равна нулю?
10 ответов
Это даже хуже, чем предполагает Юваль.
математически, учитывая вектор x, вы ищете новый вектор x|| / x//
где ||./ / это норма, о которой вы, вероятно, думаете как о евклидовой норме с
||.| / = sqrt (точка (v, v)) = sqrt(sum_i x_i**2)
Это числа с плавающей запятой, поэтому недостаточно просто защитить от деления на ноль, у вас также есть проблема с плавающей запятой, если все x_i малы (они могут underflow и вы теряете величину).
в основном все сводится к тому, что если вам действительно нужно правильно обрабатывать небольшие векторы, вам придется сделать еще немного работы.
Если малые и нулевые векторы не имеют смысла в вашем приложении, вы можете проверить величину вектора и сделать что-то соответствующее.
(обратите внимание, что как только вы начнете иметь дело с плавающей точкой, а не с реальными числами, делайте такие вещи, как квадрат, а затем квадрат укоренение чисел (или их сумм) проблематично как на больших, так и на малых концах представимого диапазона)
итог: правильная численная работа во всех случаях сложнее, чем кажется на первый взгляд.
например, с верхней части моей головы потенциальные проблемы с этой (нормализацией) операцией, выполненной наивным способом
математически говоря, нулевой вектор не может быть нормализован. Это пример того, что мы называем в вычислительной геометрии «вырожденным случаем», и это огромная тема, делающая большую головную боль для разработчиков алгоритмов геометрии. Я могу представить себе следующие подходы к проблеме.
лично я в своем коде использую 3 подхода везде. Одним из его преимуществ является то, что он не позволяет программисту забывать иметь дело с вырожденными случаями.
обратите внимание, что из-за ограниченного диапазона чисел с плавающей запятой, даже если входной вектор не равен нулевому вектору, вы все равно можете получить бесконечное координаты в выходном векторе. Из-за этого я не рассматриваю 1. подход должен быть плохим дизайнерским решением.
Как уже упоминалось несколько раз, вы не можете нормализовать нулевой вектор. Итак, ваши варианты:
Вариант 1 имеет проблему, что возвращаемое значение не будет иметь длину единицы, и поэтому он может молча вводить ошибки в вызывающий код, который предполагает, что результирующий вектор имеет длину единицы.
Вариант 2 имеет аналогичную проблему с вариантом 1, но потому, что NaNs обычно гораздо заметнее, чем нули, это, скорее всего, проявится легче.
Я думаю, что Вариант 3 будет лучшим решением, хотя это делает интерфейс более сложен. Вместо того чтобы сказать
теперь вы должны сказать что-то вроде
почти как 0/0. Следует выбросить исключение или вернуть NaN.
нулевой вектор уже нормализован, при любом определении нормы вектора, с которым я когда-либо сталкивался, так что это один случай.
Что касается вектора с компонентами, сумма которых равна нулю-это зависит от определения нормы, которую вы используете. С простой старой L2-нормой (евклидовым расстоянием между началом координат и вектором) стандартная формула для вычисления нормализованного вектора должна работать нормально, так как она сначала квадратирует отдельные компоненты.
(0,0,0) должно быть (0,0,0) нормализовано плюс предупреждение (или исключение), возможно.
математически это не определено, я думаю.
Ну, вам придется делить на ноль, чего вы не можете сделать, поэтому я думаю, что большинство языков будут иметь какое-то значение NaN.
учитывая вектор v, нормализовать его означает сохранить его направление и сделать его единичной длины, умножив его на хорошо выбранный коэффициент.
Это явно невозможно для нулевого вектора, потому что он действительно не имеет направления или потому, что его длина не может быть изменена путем мутлирования его некоторым фактором (он всегда будет равен нулю).
Я бы предложил, чтобы любая процедура, для которой вы хотели бы использовать свой вектор, и это требует, чтобы этот вектор был нормализовано, не определено для нулевых векторов.
все зависит от того, как вы определяете «нормализовать». Одним из возможных расширений термина является то, что результатом этой операции является любой вектор единичной длины (я в основном использую (1, 0, 0) здесь). Это полезно, например, когда требуется нормализация для возврата направления к границе круга из заданной точки.




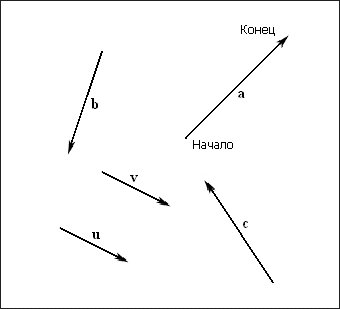
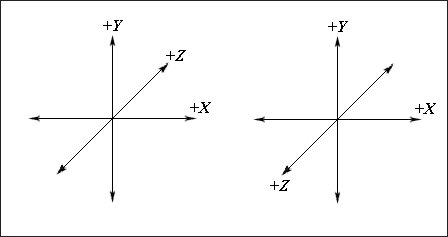
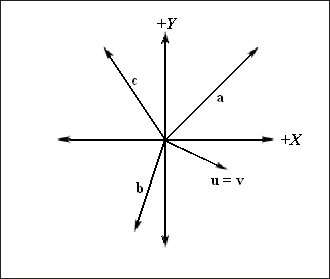
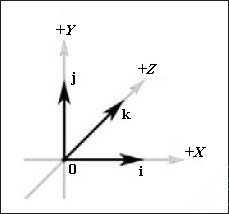
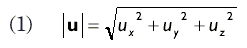
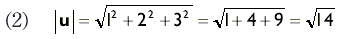
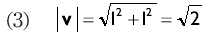
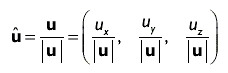
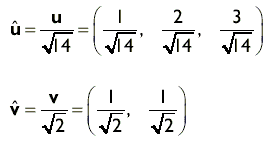
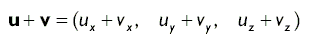
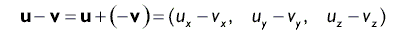
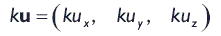
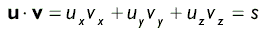
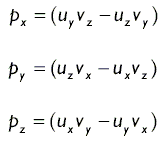
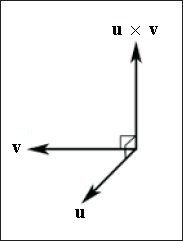
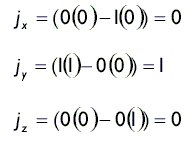

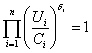 .
.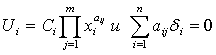 .
.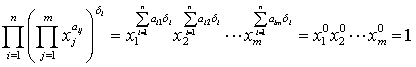 .
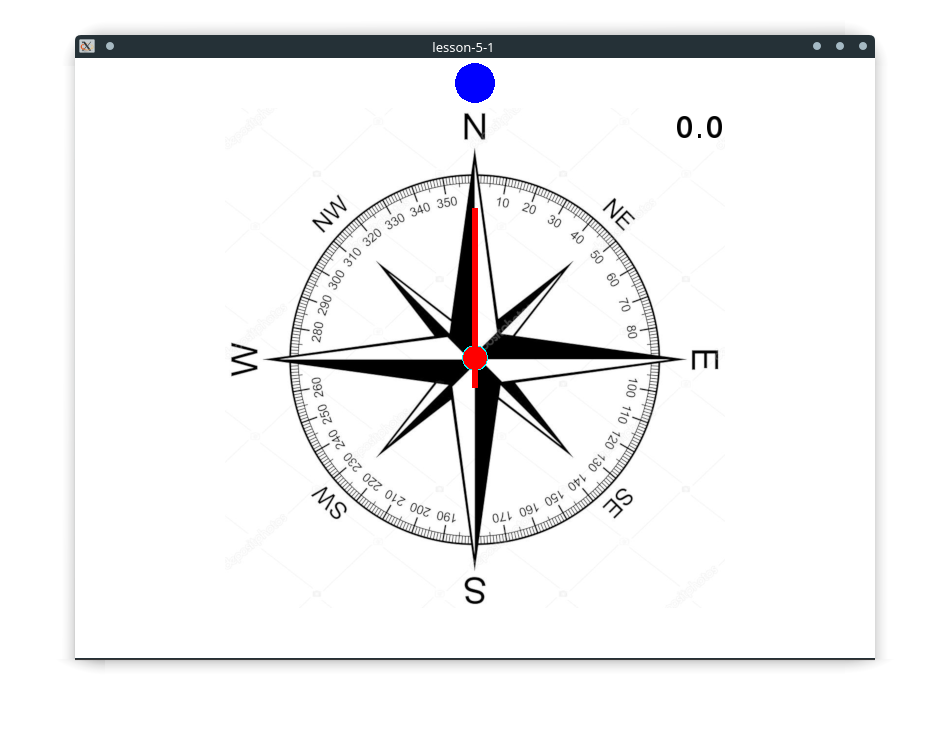
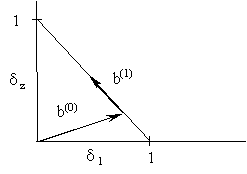
.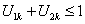 . Из соотношения пропорциональности:
. Из соотношения пропорциональности: 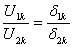 , можно получить:
, можно получить: 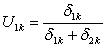 .
.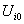 — для ЦФ и
— для ЦФ и 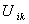 — для ограничений, а также учитывая, что
— для ограничений, а также учитывая, что 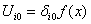 , из основного тождества получим:
, из основного тождества получим: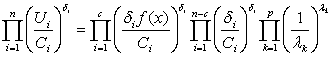 ,
,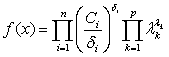 .
.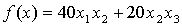
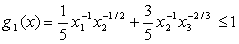 .
.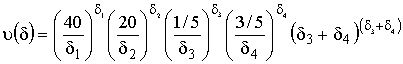 .
.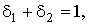
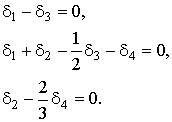
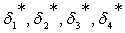 ):
):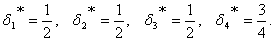
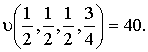
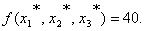
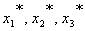 ). Исходя из смысла двойственной переменной, как весового коэффициента позинома, можно записать для ЦФ:
). Исходя из смысла двойственной переменной, как весового коэффициента позинома, можно записать для ЦФ: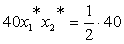 и
и 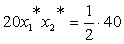 ,
,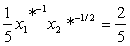 и
и 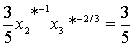 .
.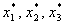 , прологарифмируем обе части соотношений представленных выше соотношений. Мы получим, что
, прологарифмируем обе части соотношений представленных выше соотношений. Мы получим, что 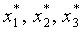 , удовлетворяет системе:
, удовлетворяет системе: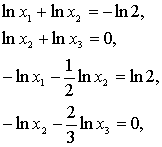
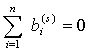 .
.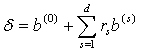 .
.
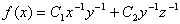 при условии
при условии 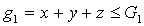 .
. .
.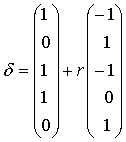
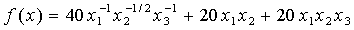
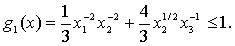
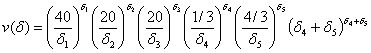
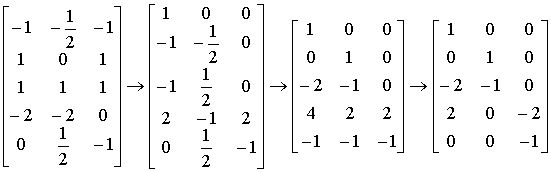 (2-8)
(2-8) , (2-9)
, (2-9)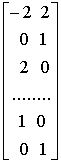 . (2-10)
. (2-10)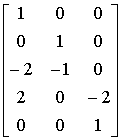 (2-11) и
(2-11) и 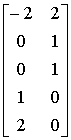 . (2-12)
. (2-12)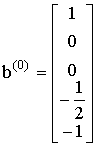 , (2-13)
, (2-13)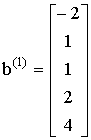 . (2-14)
. (2-14)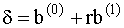
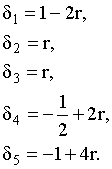 (2-15)
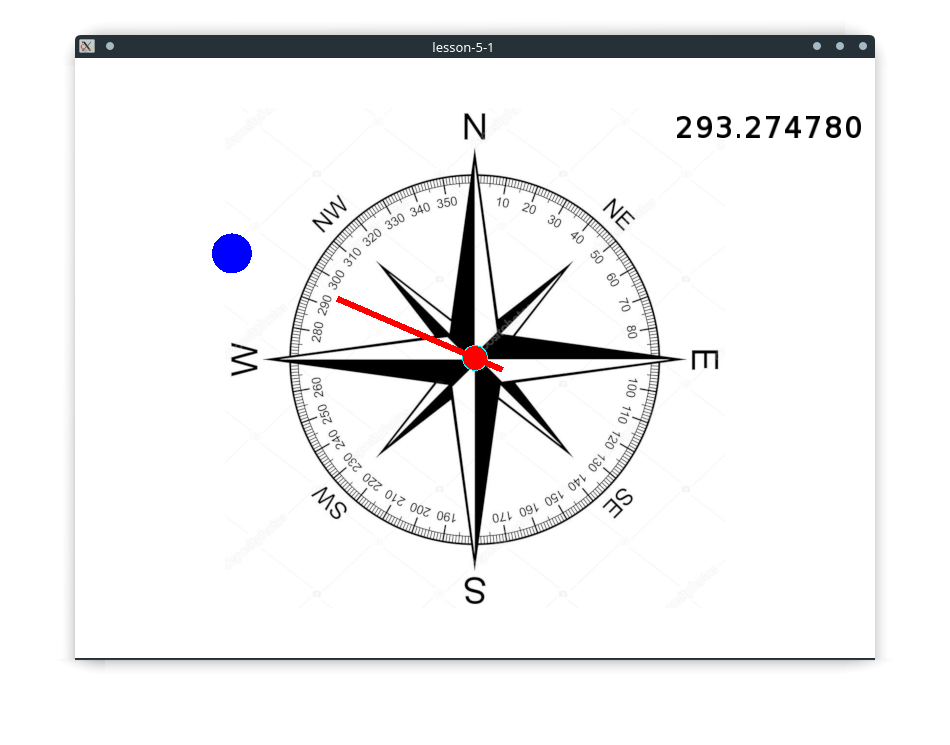
(2-15)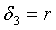 получается аналогичный результат. Из полученных уравнений ясно, что δ удовлетворяет условиям неотрицательности только при таких значениях r:
получается аналогичный результат. Из полученных уравнений ясно, что δ удовлетворяет условиям неотрицательности только при таких значениях r: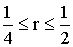 (2-16)
(2-16)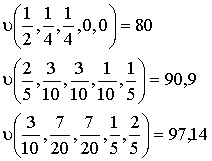 (2-17)
(2-17)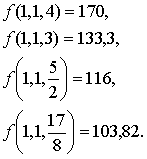 (2-18)
(2-18)