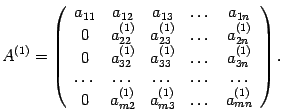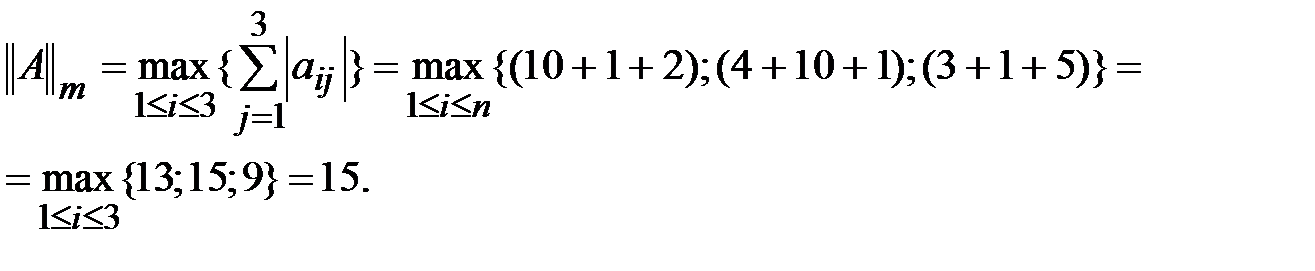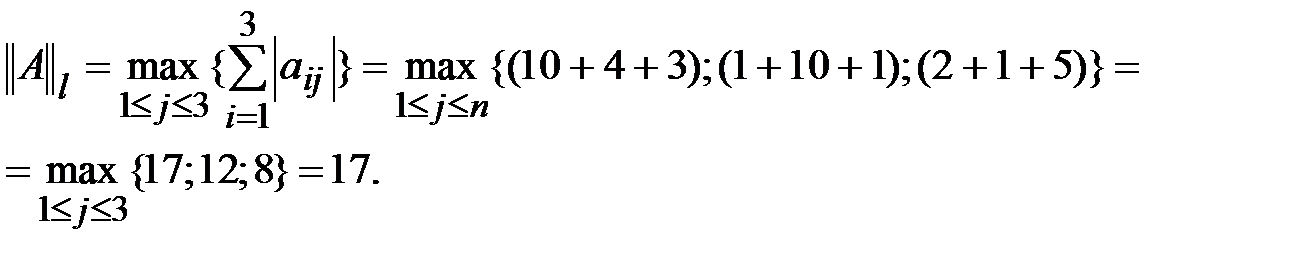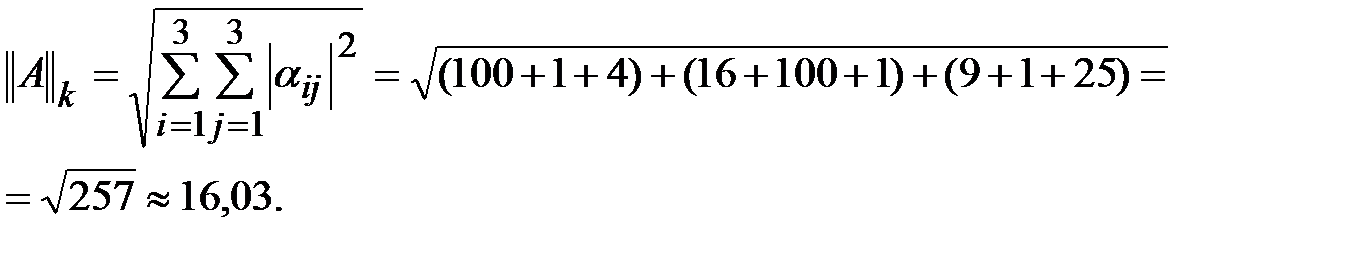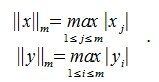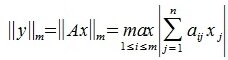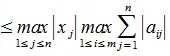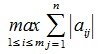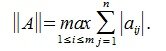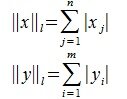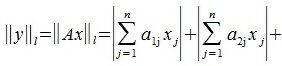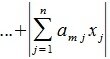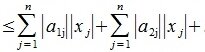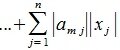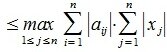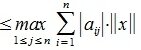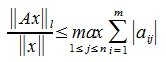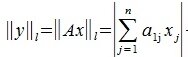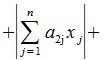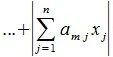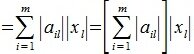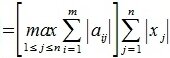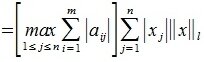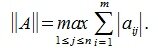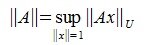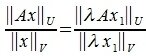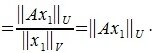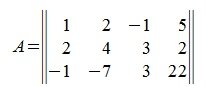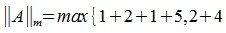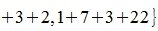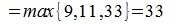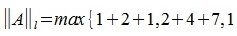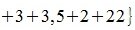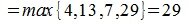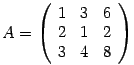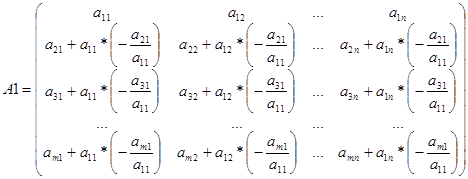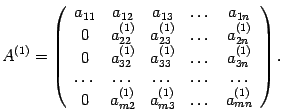что такое норма матрицы
учимся
программировать
Программированию нельзя научить, можно только научится
Главная » Уроки по Численным методам » Урок 12. Ранг матрицы. Вычисление ранга матрицы. Норма матриц
Урок №12. Ранг матрицы. Вычисление ранга матрицы. Норма матриц.
Если все миноры матрицы Aпорядка kравны нулю, то все миноры порядка k+1, если такие существуют, тоже равны нулю.
Рангом матрицы A называется наибольший из порядков миноров матрицы A, отличных от нуля.
Максимум ранг может быть равен минимальному числу из количества строк или столбцов матрицы, т.е. если матрица имеет размер 4х5, то максимум ранг будет 4.
Минимум ранг матрицы равен 1, если только вы не имеете дело с нулевой матрицей, там всегда ранг равен нулю.
Ранг невырожденной квадратной матрицы порядка n равен n, так как ее определитель является минором порядка n и у невырожденной матрицы отличен от нуля.
При транспонировании матрицы ее ранг не меняется.
Пусть ранг матрицы равен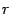 
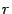
. Тогда любой минор порядка 
, отличный от нуля, называется базисным минором.
Пример. Дана матрица А.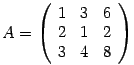 
Определитель матрицы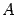 
равен нулю.
Минор второго порядка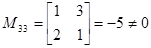 
. Следовательно, r(A)=2 и минор базисный.
Базисным минором является также минор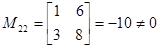 
.
Минор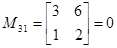 
, т.к. =0, поэтому не будет базисным.
Задание: самостоятельно проверить, какие еще миноры второго порядка будут базисными, а какие нет.
Нахождение ранга матрицы с помощью вычисления всех ее миноров требует слишком большой вычислительной работы. (Читатель может проверить, что в квадратной матрице четвертого порядка 36 миноров второго порядка.) Поэтому для нахождения ранга применяется другой алгоритм. Для его описания потребуется ряд дополнительных сведений.
Назовем элементарными преобразованиями матриц следующие действия над ними:
1) перестановка строк или столбцов;
2) умножение строки или столбца на число отличное от нуля;
3) добавление к одной из строк другой строки, умноженной на число или добавление к одному из столбцов другого столбца, умноженного на число.
При элементарных преобразованиях ранг матрицы не меняется.
Алгоритм вычисления ранга матрицы похож на алгоритм вычисления определителя и заключается в том, что с помощью элементарных преобразований матрица приводится к простому виду, для которого найти ранг не представляет труда. Так как при каждом преобразовании ранг не менялся, то, вычислив ранг преобразованной матрицы, мы тем самым находим ранг исходной матрицы.
Пусть требуется вычислить ранг матрицы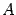 
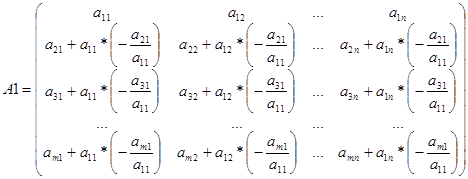
размеров mxn.
В результате расчетов матрица А1 имеет вид 
В лабораторно-практической работе рассмотрим пример нахождения ранга матрицы.
Вторая норма матрицы представляет из себя квадратный корень из суммы квадратов всех элементов матрицы. А это значит мы возводим в квадрат все элементы матрицы, затем складываем полученные значения и из результата извлекаем квадратный корень.
В нашем случае, 2 норма матрицы получилась равна квадратному корню из 269. На схеме, я приближенно извлекла квадратный корень из 269 и в результате получила приблизительно около 16,401. Хотя более правильно не извлекать корень. 
Как вычислить норму матрицы
Нормы матриц часто используются при определении погрешности различных численных методов. В частности, в итерационных методах решения систем линейных алгебраических уравнений они применяются для того, чтобы определить погрешность решения, найденного на каждой итерации.
Как правило, используются нормы трех видов.
1) M-норма. Вычисляется по формуле
, где i – номер строки, j – номер столбца.
Пример.Для матрицы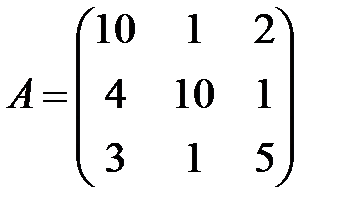 
m-норма равна 
2) L-норма. Вычисляется по формуле
, где i – номер строки, j – номер столбца.
Пример.Для матрицы 
l-норма равна 
3) K-норма. Вычисляется по формуле
, где i – номер строки, j – номер столбца.
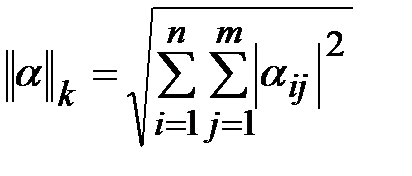
Пример.Для матрицы 
k-норма равна 
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8444 – 
| 7337 – 
или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Определим норму матрицы A равенством:
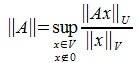 | (1) |
Из определения нормы матрицы следует:
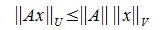 | (2) |
Пусть для двух матриц A и B порядка m×n определены одни и те же векторные нормы. Тогда имеем соотношение:
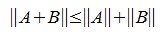 | (3) |
Кроме того справедливо равенство
Пусть для m×n матрицы A и n×k матрицы B определены матричные нормы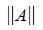 
, 
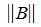
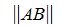
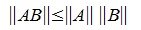
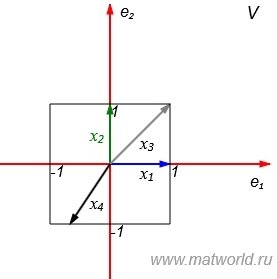
и пусть для m×k матрицы AB определена норма 
. Тогда
.
1. Пусть в пространствах V и U введена векторная норма
В (5) и (6) неравнетство превращается в равенство, если взять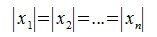 
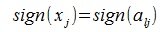
и 
, j=1. n, где l-то значение i, при котором
достигает своего максимума. Учитывая высшеизложенное, неравенство (6) и равенство (1), получим:
2. Введем в пространствах V и U векторную норму
Пусть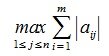 
достигается при j=l. Для вектора x, у которого только один элемент отлично от нуля, имеем:
Учитывая (1),(8) и (9) получим l-норму матрицы A:
Норму матрицы, определяемую с помощью формулы (1), называется операторной нормой, подчиненной данной норме векторов.
Отметим, что определение нормы матрицы (1) эквивалентно следующему определению:
Действительно, любой ненулевой вектор x∈V можно представить в виде произведения λx₁, где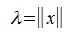 
, 
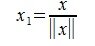
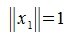
. Тогда, учитывая, что 
, получим:
Примеры вычисления нормы матрицы
Вычислим m-норму и l-норму матрицы используя (7) и (10).
Геометрическая интерпретация нормы матрицы
Пусть в линейном пространстве V введена m-норма для всех векторов x∈V:
.
Найдем норму матрицы
.
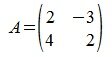
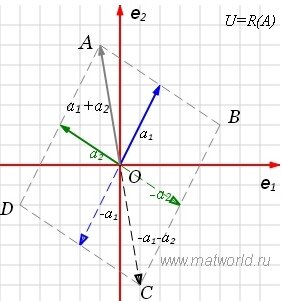
На рисунке рис. 2 изображено пространство столбцов матрицы A. Каждому вектору x∈X соответствует вектор Ax в U. Конечные точки этих векторов находятся на пунктирном четырехугольнике ABCD. m-норма матрицы A – это модуль наибольшго координата наибольшего из векторов, конечная точка которого находится на четырехугольнике ABCD. На рис.2 это векторы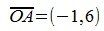 
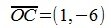
и 
а модуль наибольшего координата 6. Используя (3), аналитически получим тот же результат.
Отметим, что норма матрицы показывает насколько максимально растягивается вектор x при отображении y=Ax. В нашем примере векторы х растягиваются максимально 6 раз.
Программированию нельзя научить, можно только научится
Главная » Уроки по Численным методам » Урок 12. Ранг матрицы. Вычисление ранга матрицы. Норма матриц
Если все миноры матрицы Aпорядка kравны нулю, то все миноры порядка k+1, если такие существуют, тоже равны нулю.
Рангом матрицы A называется наибольший из порядков миноров матрицы A, отличных от нуля.
Максимум ранг может быть равен минимальному числу из количества строк или столбцов матрицы, т.е. если матрица имеет размер 4х5, то максимум ранг будет 4.
Минимум ранг матрицы равен 1, если только вы не имеете дело с нулевой матрицей, там всегда ранг равен нулю.
Ранг невырожденной квадратной матрицы порядка n равен n, так как ее определитель является минором порядка n и у невырожденной матрицы отличен от нуля.
При транспонировании матрицы ее ранг не меняется.
Пусть ранг матрицы равен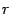 
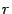
. Тогда любой минор порядка 
, отличный от нуля, называется базисным минором.
Пример. Дана матрица А.
Определитель матрицы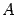 
равен нулю.
Минор второго порядка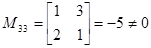 
. Следовательно, r(A)=2 и минор базисный.
Базисным минором является также минор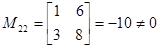 
.
Минор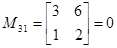 
, т.к. =0, поэтому не будет базисным.
Задание: самостоятельно проверить, какие еще миноры второго порядка будут базисными, а какие нет.
Нахождение ранга матрицы с помощью вычисления всех ее миноров требует слишком большой вычислительной работы. (Читатель может проверить, что в квадратной матрице четвертого порядка 36 миноров второго порядка.) Поэтому для нахождения ранга применяется другой алгоритм. Для его описания потребуется ряд дополнительных сведений.
Назовем элементарными преобразованиями матриц следующие действия над ними:
1) перестановка строк или столбцов;
2) умножение строки или столбца на число отличное от нуля;
3) добавление к одной из строк другой строки, умноженной на число или добавление к одному из столбцов другого столбца, умноженного на число.
При элементарных преобразованиях ранг матрицы не меняется.
Алгоритм вычисления ранга матрицы похож на алгоритм вычисления определителя и заключается в том, что с помощью элементарных преобразований матрица приводится к простому виду, для которого найти ранг не представляет труда. Так как при каждом преобразовании ранг не менялся, то, вычислив ранг преобразованной матрицы, мы тем самым находим ранг исходной матрицы.
Пусть требуется вычислить ранг матрицы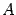 
размеров mxn.
В результате расчетов матрица А1 имеет вид 
В предложенном алгоритме нахождения ранга матрицы все вычисления должны производиться без округлений. Сколь угодно малое изменение хотя бы в одном из элементов промежуточных матриц может привести к тому, что полученный ответ будет отличаться от ранга исходной матрицы на несколько единиц.
Если в исходной матрице элементы были целыми числами, то и вычисления удобно производить без использования дробей. Поэтому на каждом этапе целесообразно умножать строки на такие числа, чтобы при вычислениях дроби не возникали.
В лабораторно-практической работе рассмотрим пример нахождения ранга матрицы.
Рисунок 10.
Вторая норма матрицы представляет из себя квадратный корень из суммы квадратов всех элементов матрицы. А это значит мы возводим в квадрат все элементы матрицы, затем складываем полученные значения и из результата извлекаем квадратный корень.
В нашем случае, 2 норма матрицы получилась равна квадратному корню из 269. На схеме, я приближенно извлекла квадратный корень из 269 и в результате получила приблизительно около 16,401. Хотя более правильно не извлекать корень. 
СОДЕРЖАНИЕ
Предварительные мероприятия
Каждую норму на K n × n можно масштабировать до субмультипликативной; в некоторых книгах норма терминологической матрицы зарезервирована для субмультипликативных норм.
Матричные нормы, индуцированные векторными нормами
Более того, любая индуцированная норма удовлетворяет неравенству
имеющий нулевой спектральный радиус. В любом случае для квадратных матриц мы имеем формулу спектрального радиуса :
Совместимые и последовательные нормы
Особые случаи
это просто максимальная абсолютная сумма столбцов матрицы;
что является просто максимальной абсолютной суммой строк матрицы.
Матричные нормы «по входу»
L 2,1 и L p, q нормы
Норма Фробениуса
Норма Фробениуса является расширением евклидовой нормы и происходит от внутреннего произведения Фробениуса на пространстве всех матриц. K п × п <\ Displaystyle К ^ <п \ раз п>> 
Это также удовлетворяет
Макс норма
Максимальная норма является нормой поэлементно с р = д = ∞:
Нормы Шаттена
Наиболее известные случаи: p = 1, 2, ∞. Случай p = 2 дает норму Фробениуса, введенную ранее. Случай p = ∞ дает спектральную норму, которая является операторной нормой, индуцированной векторной 2-нормой (см. Выше). Наконец, p = 1 дает ядерную норму (также известную как норма следа или n-норма Ky Fan ), определяемую как
Монотонные нормы
Норма Фробениуса и спектральная норма являются примерами монотонных норм.
Нормы сокращения
Эквивалентность норм
Для любых двух матричных норм и мы имеем следующее: ‖ ⋅ ‖ α <\ displaystyle \ | \ cdot \ | _ <\ alpha>> ‖ ⋅ ‖ β <\ displaystyle \ | \ cdot \ | _ <\ beta>>
Примеры эквивалентности норм
Еще одно полезное неравенство между матричными нормами:
СОДЕРЖАНИЕ
Предварительные мероприятия
Каждую норму на K n × n можно масштабировать до субмультипликативной; в некоторых книгах норма терминологической матрицы зарезервирована для субмультипликативных норм.
Матричные нормы, индуцированные векторными нормами
Более того, любая индуцированная норма удовлетворяет неравенству
имеющий нулевой спектральный радиус. В любом случае для квадратных матриц мы имеем формулу спектрального радиуса :
Совместимые и последовательные нормы
Особые случаи
это просто максимальная абсолютная сумма столбцов матрицы;
что является просто максимальной абсолютной суммой строк матрицы.
Матричные нормы «по входу»
L 2,1 и L p, q нормы
Норма Фробениуса
Норма Фробениуса является расширением евклидовой нормы и происходит от внутреннего произведения Фробениуса на пространстве всех матриц. K п × п <\ Displaystyle К ^ <п \ раз п>>
Это также удовлетворяет
Макс норма
Максимальная норма является нормой поэлементно с р = д = ∞:
Нормы Шаттена
Наиболее известные случаи: p = 1, 2, ∞. Случай p = 2 дает норму Фробениуса, введенную ранее. Случай p = ∞ дает спектральную норму, которая является операторной нормой, индуцированной векторной 2-нормой (см. Выше). Наконец, p = 1 дает ядерную норму (также известную как норма следа или n-норма Ky Fan ), определяемую как
Монотонные нормы
Норма Фробениуса и спектральная норма являются примерами монотонных норм.
Нормы сокращения
Эквивалентность норм
Для любых двух матричных норм и мы имеем следующее: ‖ ⋅ ‖ α <\ displaystyle \ | \ cdot \ | _ <\ alpha>> ‖ ⋅ ‖ β <\ displaystyle \ | \ cdot \ | _ <\ beta>>
Примеры эквивалентности норм
Еще одно полезное неравенство между матричными нормами:
От действий над матрицами к пониманию их сути…
Очень уважаю людей, которые имеют смелость заявить, что они что-то не понимают. Сам такой. То, что не понимаю, — обязательно должен изучить, осмыслить, понять. Статья «Математика на пальцах», и особенно матричная запись формул, заставили меня поделиться своим небольшим, но, кажется, немаловажным опытом работы с матрицами.
Лет эдак 20 назад довелось мне изучать высшую математику в вузе, и начинали мы с матриц (пожалуй, как и все студенты того времени). Почему-то считается, что матрицы — самая лёгкая тема в курсе высшей математики. Возможно — потому, что все действия с матрицами сводятся к знанию способов расчёта определителя и нескольких формул, построенных — опять же, на определителе. Казалось бы, всё просто. Но… Попробуйте ответить на элементарный вопрос — что такое определитель, что означает число, которое вы получаете при его расчёте? (подсказка: вариант типа «определитель — это число, которое находится по определённым правилам» не является правильным ответом, поскольку говорит о методе получения, а не о самой сути определителя). Сдаётесь? — тогда читаем дальше.
Сразу хочу сказать, что я не математик ни по образованию, ни по должности. Разве что мне интересна суть вещей, и я порой пытаюсь до них «докопаться». Так же было и с определителем: нужно было разобраться со множественной регрессией, а в этом разделе эконометрики практически всё делается через… матрицы, будь они неладны. Вот и пришлось мне самому провести небольшое исследование, поскольку ни один из знакомых математиков не дал внятного ответа на поставленный вопрос, изначально звучавший как «что такое определитель». Все утверждали, что определитель — это такое число, которое особым образом посчитано, и если оно равно нулю, то… В общем, как в любом учебнике по линейной алгебре. Спасибо, проходили.
Если какую-то идею придумал один человек, то другой человек должен быть в состоянии её понять (правда, для этого порой приходится вооружаться дополнительными знаниями). Обращение к «великому и могучему» поисковику показало, что «площадь параллелограмма равна модулю определителя матрицы, образованной векторами — сторонами параллелограмма». Говоря простым языком, если матрица — это способ записи системы уравнений, то каждое уравнение в отдельности описывает вектор. Построив из точки начала координат векторы, заданные в матрице, мы таким образом зададим в пространстве некоторую фигуру. Если наше пространство одномерное, то фигура — это отрезок; если двумерное — то фигура — параллелограмм, и так далее.
Получается, что для одномерного пространства определитель — это длина отрезка, для плоскости — площадь фигуры, для трёхмерной фигуры — её объём… дальше идут n-мерные пространства, вообразить которые нам не дано. Если объём фигуры (то есть определитель для матрицы 3*3) равен нулю, то это означает, что сама фигура не является трёхмерной (она может быть при этом двухмерной, одномерной или вообще представлять собой точку). Ранг матрицы — это истинная (максимальная) размерность пространства, для которого определитель не равен нулю.
Так, с определителем почти всё понятно: он определяет «объёмность» фигуры, образованной описанными системой уравнений векторами (хотя непонятно, почему его значение не зависит от того, имеем мы дело с исходной матрицей, или с транспонированной — возможно, транспонирование — это вид аффинного преобразования?). Теперь нужно разобраться с действиями над матрицами…
Если матрица — это система уравнений (а иначе зачем нам таблица каких-то цифр, не имеющих к реальности никакого отношения?), то мы можем с ней делать разные вещи. Например, можем сложить две строки одной и той же матрицы, или умножить строку на число (то есть каждый коэффициент строки умножаем на одно и то же число). Если у нас есть две матрицы с одинаковыми размерностями, то мы их можем сложить (главное, чтобы при этом мы не сложили бульдога с носорогом — но разве математики, разрабатывая теорию матриц, думали о таком варианте развития событий?). Интуитивно понятно, тем более что в линейной алгебре иллюстрациями подобных операций являются системы уравнений.
Однако в чём смысл умножения матриц? Как я могу умножить одну систему уравнений на другую? Какой смысл будет иметь то, что я получу в этом случае? Почему для умножения матриц неприменимо переместительное правило (то есть произведение матриц В*А не то что не равно произведению А*В, но и не всегда осуществимо)? Почему, если мы перемножим матрицу на вектор-столбец, то получим вектор-столбец, а если перемножим вектор-строку на матрицу, то получим вектор-строку?
Ну, тут уж не то что Википедия, — тут даже современные учебники по линейной алгебре бессильны дать какое-либо внятное объяснение. Поскольку изучение чего-либо по принципу «вы сначала поверьте — а поймёте потом» — не для меня, копаю в глубь веков (точнее — читаю учебники первой половины XX века) и нахожу интересную фразу…
Если совокупность обычных векторов, т.е. направленных геометрических отрезков, является трёхмерным пространством, то часть этого пространства, состоящая из векторов, параллельных некоторой плоскости, является двумерным пространством, а все векторы, параллельные некоторой прямой, образуют одномерное векторное пространство.
В книгах об этом напрямую не говорится, но получается, что векторам, параллельным некоторой плоскости, необязательно лежать на этой плоскости. То есть они могут находиться в трёхмерном пространстве где угодно, но если они параллельны именно этой плоскости, то они образуют двумерное пространство… Из приходящих мне на ум аналогий — фотография: трёхмерный мир представлен на плоскости, при этом вектору, параллельному матрице (или плёнке) фотоаппарата, будет соответствовать такой же вектор на картинке (при условии соблюдении масштаба 1:1). Отображение трёхмерного мира на плоскости «убирает» одно измерение («глубину» картинки). Если я правильно понял сложные математические концепции, перемножение двух матриц как раз и представляет собой подобное отражение одного пространства в другом. Поэтому, если отражение пространства А в пространстве В возможно, то допустимость отражения пространства В в пространстве А — не гарантируется.
Любая статья заканчивается в тот момент, когда автору надоедает её писать. Поскольку я не ставил перед собой цели объять необъятное, а исключительно хотел понять суть описанных операций над матрицами и то, как именно матрицы связаны с решаемыми мной системами уравнений, я не полез в дальнейшие дебри линейной алгебры, а вернулся к эконометрике и множественной регрессии, но сделал это уже более осознанно. Понимая, что и зачем я делаю и почему только так, а не иначе. То, что у меня получилось в этом материале, можно озаглавить как «глава о сути основных операций линейной алгебры, которую почему-то забыли напечатать в учебниках». Но ведь мы же не читаем учебников, правда? Если честно, когда я учился в университете, мне очень не хватало именно понимания затронутых здесь вопросов, поэтому я надеюсь, что, изложив этот непростой материал по возможности простыми словами, я делаю доброе дело и помогаю кому-то вникнуть в саму суть матричной алгебры, переведя операции над матрицами из раздела «камлание с бубном» в раздел «практические инструменты, применяемые осознанно».