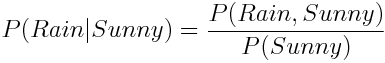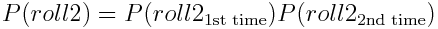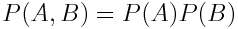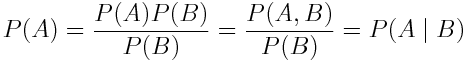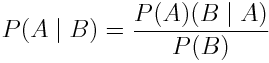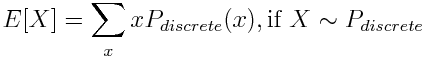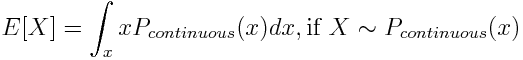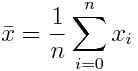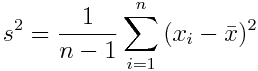что такое независимые события

Независимые события

Содержание

Основные определения [ править ]

[math] \Leftarrow [/math] :

Примеры [ править ]

Игральная кость [ править ]

[math] A = \<2,4,6\>\ p(A)=\dfrac<1> <2>[/math] — вероятность выпадения чётной цифры

[math] B=\<1,2,3\>\ p(B)=\dfrac<1> <2>[/math] — вероятность выпадения одной из первых трёх цифр

Карты [ править ]

[math] A = \<(1,j)\>\ p(A)=\dfrac<1> <4>[/math] — вероятность выпадения карты заданной масти

[math] B=\<(i,1)\>\ p(B)=\dfrac<1> <13>[/math] — вероятность выпадения карты заданного достоинства

[math] p(A \cap B)=p(\<(1,1)\>)=\dfrac<1><52>[/math] — вероятность выпадения карты заданной масти и заданного достоинства

Честная монета [ править ]

[math] A = \<0\>\ [/math] — выпадение орла

[math] B=\<1\>\ [/math] — выпадение решки

Тетраэдр Бернштейна [ править ]

Попарно независимые события и события, независимые в совокупности — это не одно и то же.

Рассмотрим правильный тетраэдр, три грани которого окрашены соответственно в красный, синий, зелёный цвета, а четвёртая грань содержит все три цвета.

[math] A [/math] — выпадение грани, содержащей красный цвет

[math] B [/math] — выпадение грани, содержащей синий цвет

[math] C [/math] — выпадение грани, содержащей зеленый цвет

Так как каждый цвет есть на двух гранях из четырёх, вероятность каждого из этих событий равна:

Так как одна грань содержит все три цвета, а остальные — по одному, то вероятность пересечения любых двух событий равна: [math]p(A \cap B)=p(A \cap C)=p(B \cap C)=\dfrac <1> <4>[/math]

[math]p(A) \cdot p(B)=p(A) \cdot p(C)=p(B) \cdot p(C)=\dfrac<1><2>\cdot\dfrac<1><2>=\dfrac<1><4>[/math]

Все события попарно независимы, так как:

[math]p(A \cap B)=p(A) \cdot p(B)[/math]

[math]p(A \cap C)=p(A) \cdot p(C)[/math]

[math]p(B \cap C)=p(B) \cdot p(C)[/math]

Вероятность пересечения всех трёх равна: [math]p(A \cap B \cap C)=\dfrac<1><4>[/math]

[math]p(A) \cdot p(B) \cdot p(C)=\dfrac<1><2>\cdot\dfrac<1><2>\cdot\dfrac<1><2>=\dfrac<1><8>[/math]

Cобытия не являются независимыми в совокупности, так как: [math]p(A \cap B \cap C) \neq p(A) \cdot p(B) \cdot p(C)[/math]

Получили, что события являются попарно независимыми, но не являются независимыми в совокупности, значит, эти два понятия — не одно и то же, что мы и хотели показать.

Источник

Теория вероятности. Часть 2

В заданиях ЕГЭ по математике встречаются и более сложные задачи на вероятность (нежели мы рассматривали в части 1), где приходится применять правило сложения, умножения вероятностей, различать совместные и несовместные события.

Совместные и несовместные события

События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.

Например, бросая игральную кость, можно выделить такие события, как выпадение четного числа очков и выпадение нечетного числа очков. Эти события несовместны.

События называются совместными, если наступление одного из них не исключает наступления другого.

Например, бросая игральную кость, можно выделить такие события, как выпадение нечетного числа очков и выпадение числа очков, кратных трем. Когда выпадает три, реализуются оба события.

Сумма событий

Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.

При этом сумма двух несовместных событий есть сумма вероятностей этих событий:

Например, вероятность выпадения 5 или 6 очков на игральном кубике при одном броске, будет , потому что оба события (выпадение 5, выпадение 6) неовместны и вероятность реализации одного или второго события вычисляется следующим образом:

Вероятность же суммы двух совместных событий равна сумме вероятностей этих событий без учета их совместного появления:

Например, в торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдем вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов (то есть или в одном, или в другом, или в обоих сразу).

Вероятность первого события «кофе закончится в первом автомате» также как и вероятность второго события «кофе закончится во втором автомате» по условию равна 0,3. События являются совместными.

Вероятность совместной реализации первых двух событий по условию равна 0,12.

Значит, вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов есть

Зависимые и независимые события

Два случайных события А и В называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события А и В называют зависимыми.

Например, при одновременном броске двух кубиков выпадение на одном из них, скажем 1, и на втором 5, – независимые события.

Произведение вероятностей

Произведением (или пересечением) нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

Если происходят два независимых события А и В с вероятностями соответственно Р(А) и Р(В), то вероятность реализации событий А и В одновременно равна произведению вероятностей:

Например, нас интересует выпадение на игральном кубике два раза подряд шестерки. Оба события независимы и вероятность реализации каждого из них по отдельности – . Вероятность того, что произойдут оба эти события будет вычисляться по указанной выше формуле: .

Подборку задач на отработку темы смотрите здесь.

Источник

Теория вероятности. Часть 2

В заданиях ЕГЭ по математике встречаются и более сложные задачи на вероятность (нежели мы рассматривали в части 1), где приходится применять правило сложения, умножения вероятностей, различать совместные и несовместные события.

Совместные и несовместные события

События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.

Например, бросая игральную кость, можно выделить такие события, как выпадение четного числа очков и выпадение нечетного числа очков. Эти события несовместны.

События называются совместными, если наступление одного из них не исключает наступления другого.

Например, бросая игральную кость, можно выделить такие события, как выпадение нечетного числа очков и выпадение числа очков, кратных трем. Когда выпадает три, реализуются оба события.

Сумма событий

Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.

При этом сумма двух несовместных событий есть сумма вероятностей этих событий:

Например, вероятность выпадения 5 или 6 очков на игральном кубике при одном броске, будет , потому что оба события (выпадение 5, выпадение 6) неовместны и вероятность реализации одного или второго события вычисляется следующим образом:

Вероятность же суммы двух совместных событий равна сумме вероятностей этих событий без учета их совместного появления:

Например, в торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдем вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов (то есть или в одном, или в другом, или в обоих сразу).

Вероятность первого события «кофе закончится в первом автомате» также как и вероятность второго события «кофе закончится во втором автомате» по условию равна 0,3. События являются совместными.

Вероятность совместной реализации первых двух событий по условию равна 0,12.

Значит, вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов есть

Зависимые и независимые события

Два случайных события А и В называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события А и В называют зависимыми.

Например, при одновременном броске двух кубиков выпадение на одном из них, скажем 1, и на втором 5, – независимые события.

Произведение вероятностей

Произведением (или пересечением) нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

Если происходят два независимых события А и В с вероятностями соответственно Р(А) и Р(В), то вероятность реализации событий А и В одновременно равна произведению вероятностей:

Например, нас интересует выпадение на игральном кубике два раза подряд шестерки. Оба события независимы и вероятность реализации каждого из них по отдельности – . Вероятность того, что произойдут оба эти события будет вычисляться по указанной выше формуле: .

Подборку задач на отработку темы смотрите здесь.

Источник

Теория вероятностей для самых маленьких

Авторизуйтесь

Теория вероятностей для самых маленьких

директор по технологиям в «Синимекс Дата Лаб»

В этой статье мы рассмотрим основы статистики, полезные изучающим машинное обучение, а также желающим освежить свои знания. Понятия, о которых пойдет речь ниже, встречаются в очень разнообразных контекстах, а также лежат в основе всеми любимого data science. Всегда полезно повторить азы теории, так как зачастую это помогает открыть для себя что-то новое, на что раньше не обращали внимание. Поэтому, начнем.

Вероятности

Зачем нам нужны вероятности, когда мы обладаем таким мощным математическим инструментарием? У нас есть матанализ для работы с функциями на бесконечно малых величинах и оценки их динамики. У нас есть алгебра для решения уравнений, а также десятки других областей математики, с помощью которых мы можем решить едва ли не любую задачу.

Проблема в том, что мы живем в хаотичной вселенной, где точные измерения чаще всего невозможны. Изучая реальные процессы, происходящие в мире, мы хотим понять, какие случайные события влияют на наши эксперименты. Нас окружает неопределенность, и важно уметь «обуздать» и использовать ее в своих целях. Именно в такие моменты в ход идет теория вероятностей и статистика.

В наш век именно эти дисциплины лежат в основе искусственного интеллекта, физики элементарных частиц, обществознания, биоинформатики.

Перед тем как говорить о статистике, необходимо определиться с понятием вероятности. Как ни странно, однозначного ответа нет. Рассмотрим несколько теоретических подходов к определению вероятности.

Частотная вероятность

Представим, что нам дали монету, и мы хотим определить является ли она честной. Как это можно сделать? Подбросим ее несколько раз и запишем как 1, если выпадет орёл, 0 – если выпадет решка. Повторим этот эксперимент 1000 раз, и подсчитаем все 0 и 1. Допустим, по результатам этого утомительного процесса мы насчитали 600 орлов (1) и 400 решек (0). Если мы посчитаем частоту, с которой нам выпадал орёл или решка, мы получим 60% и 40%, соответственно. Эти частоты могут интерпретироваться как вероятности того, что, подбросив монету, нам выпадет орёл или решка. Такой подход к вероятностям называется частотным.

Условные вероятности

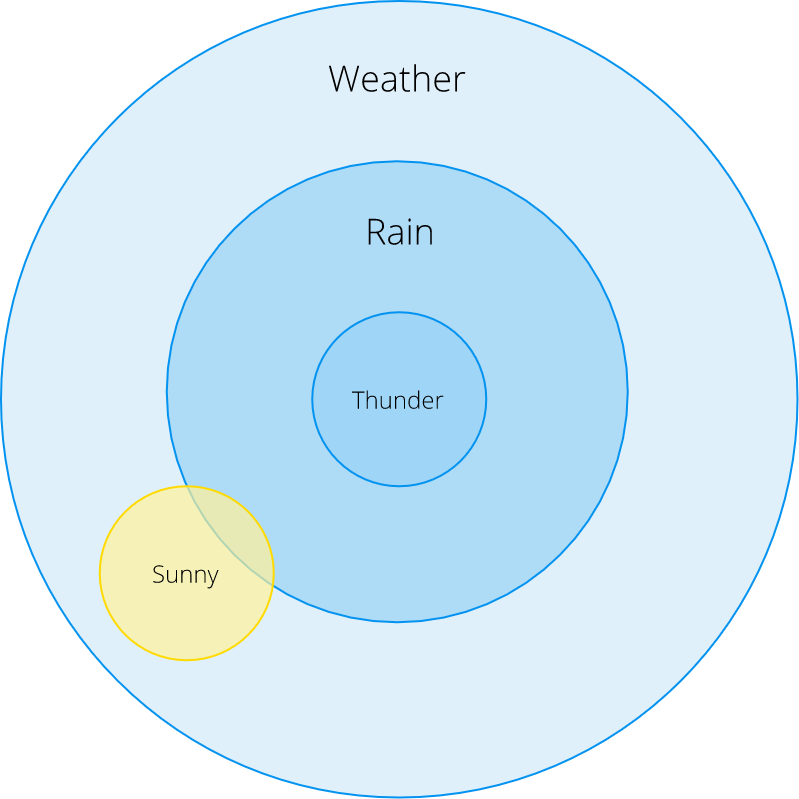
Зачастую нам нужно узнать вероятность наступления события при условии, что произошло другое событие. В этом случае, мы указываем условную вероятность события A при условии, что произошло событие B как P (A | B). Рассмотрим это на примере дождя:

Из этой диаграммы Эйлера мы видим, что P (Дождь | Гром) = 1: дождь идет всегда, когда мы слышим раскаты грома и видим молнии (в реальности это не всегда так, но примем условности для целей нашего примера).

А что насчет P (Дождь | Солнце)? На глаз, эта вероятность достаточно мала, но есть ли способ рассчитать ее точно? Условная вероятность определяется как:

Иными словами, мы должны поделить вероятность наступления обоих событий – Дождя и Солнечной погоды на вероятность события Солнечная погода.

Зависимые и независимые события

События называются независимыми, если вероятность наступления любого из них никак не зависит от наступления других событий. Например, рассмотрим вероятность того, чтобы бросить игральные кости и выкинуть две двойки подряд. Это независимые события. Иными словами,

Но почему эта формула работает? Для начала обозначим броски №1 и №2 как A и B, чтобы упростить формулу, а далее перепишем вероятность бросания костей как вероятность появления двух независимых событий:

Если формулу выше прочитать справа налево, мы увидим, что P (A | B) = P(A). По сути, это означает, что событие A не зависит от события B. Такая же логика справедлива и в отношении P(B).

Байесовский подход к вероятности

Существует еще один подход к определению вероятностей, который называется Байесовским. Частотный подход к статистике предполагает существование одной оптимальной и конкретной комбинации параметров для модели. Частотная статистика работает с неопределенностью через достаточно сложные для понимания доверительные интервалы (confidence interval). К примеру, 95% доверительный интервал в частотной статистике означает, что если бы мы проводили измерение бесконечное количество раз, то истинное значение параметра попадало бы в этот интервал в 95% случаев. Сбивает с толку, да?

С другой стороны, Байесовская теорема подходит к параметрам с вероятностных позиций и рассматривает их как случайные величины. В Байесовской статистике каждый параметр обладает собственным распределением вероятности, которое отражает, насколько вероятны данные параметры, учитывая имеющиеся в наличии данные. Математически это можно представить как:

В отличие от частотного подхода, Байесовская статистика работает с неопределенностью через достоверные интервалы (credible interval), которые интуитивно понятны. 95% достоверный интервал означает, что значение измеряемого параметра попадает в него с 95% вероятностью.

В этой ветке статистики все крутится вокруг теоремы, позволяющей рассчитать условные вероятности исходя из накопленных знаний:

Несмотря на кажущуюся простоту, Теорема Байеса имеет огромную ценность, она применяется в различных областях, и даже существует отдельная ветвь статистики, которая называется Байесовская статистика. Если интересно понять, как выводится эта формула, то вот ссылка на отличный пост, посвященный Теореме Байеса.

Распределения

Распределение вероятностей – это закон, описывающий вероятности наступления всех возможных исходов какой-либо случайной величины, выраженных в виде математической функции. Как и любая функция, распределение может обладать параметрами, позволяющими скорректировать его характеристики.

Когда мы измеряли относительную частоту исходов такого события как подбрасывание монеты, мы на самом деле рассчитали так называемое эмпирическое распределение вероятностей. Многие процессы, отличающиеся неопределенностью, могут быть описаны в терминах распределения вероятностей. Так, например, подбрасывание монеты описывается распределением Бернулли, а если бы мы захотели рассчитать вероятность, что после n попыток выпадет орел, мы можем прибегнуть к Биномиальному распределению.

Для удобства работы с вероятностями введем новое понятие, аналогичное переменной, — случайная переменная. Каждая случайная переменная соответствует определенному распределению. Случайные величины принято обозначать заглавной буквой, а также мы можем использовать символ

, чтобы обозначить, какому распределению соответствует переменная.

Это означает, что случайная переменная X описывается распределением Бернулли, при этом вероятность успеха (выпадение орла) равна 0,6.

Непрерывное и дискретное распределение вероятностей

Распределения вероятностей бывают двух типов. Дискретное распределение описывает случайные величины, которые принимают конечное число значений, как это было в примере с монетой и распределением Бернулли. Дискретные распределения определяются Функцией распределения масс (Probability Mass Function). Непрерывное распределение описывает непрерывные случайные величины, которые (в теории) могут принимать бесчисленное число значений. Например, когда мы измеряем скорость и ускорение датчиками с высокими шумами. Непрерывные распределения определяются Функцией плотности распределения вероятности (Probability Density Function).

При расчете статистик для дискретного распределения вероятностей применяется суммирование ∑, а для непрерывного – интегралы ∫. Например, математическое ожидание будет иметь следующий вид:

Выборки и статистики

Представим, что мы хотим измерить рост людей в своем городе. Чтобы измерения были независимыми, мы оценивали рост случайных прохожих на улице. Процесс случайного отбора подмножества данных из общей (генеральной) совокупности называется выборкой.

Выборка сама по себе достаточно сложна для понимания. Для того, чтобы описать ее более понятным для человека способом используются статистические показатели – обобщающие математические функции.

С одним таким показателем вы скорее всего уже сталкивались – это арифметическое среднее.

Другой пример – это дисперсия выборки:

Данная формула характеризует разброс значений в массиве данных относительно среднего.

А если я хочу узнать больше?

Знания статистики могут пригодиться в самых неочевидных ситуациях. Как сказал известный статист Джон Тьюки: «The best thing about being a statistician is that you get to play in everyone’s backyard».

Вот небольшая подборка ресурсов для продолжения изучения математической статистики:

Источник

Зависимые и независимые случайные события.
Основные формулы сложения и умножения вероятностей

Теоремы сложения вероятностей

Найдем вероятность суммы событий и (в предположении их совместности либо несовместности).

Теорема 2.1. Вероятность суммы конечного числа несовместных событий равна сумме их вероятностей:

Пример 1. Вероятность того, что в магазине будет продана пара мужской обуви 44-го размера, равна 0,12; 45-го — 0,04; 46-го и большего — 0,01. Найти вероятность того, что будет продана пара мужской обуви не меньше 44-го размера.

Пример 2. При условиях примера 1 найти вероятность того, что очередной будет продана пара обуви меньше 44-го размера.

Решение. События «очередной будет продана пара обуви меньше 44-го размера» и «будет продана пара обуви размера не меньше 44-го» противоположные. Поэтому по формуле (1.2) вероятность наступления искомого события

Сформулируем теорему сложения вероятностей в случае двух совместных событий (будет учитываться вероятность их совместного появления).

Теорема 2.2. Вероятность суммы двух совместных событий равна сумме вероятностей этих двух событий без вероятности их совместного появления:

Зависимые и независимые события. Условная вероятность

Различают события зависимые и независимые. Два события называются независимыми, если появление одного из них не изменяет вероятность появления другого. Например, если в цехе работают две автоматические линии, по условиям производства не взаимосвязанные, то остановки этих линий являются независимыми событиями.

Пример 3. Монета брошена два раза. Вероятность появления «герба» в первом испытании (событие ) не зависит от появления или не появления «герба» во втором испытании (событие ). В свою очередь, вероятность появления «герба» во втором испытании не зависит от результата первого испытания. Таким образом, события и независимые.

Пример 4. В ящике находятся 5 резцов: два изношенных и три новых. Производится два последовательных извлечения резцов. Определить условную вероятность появления изношенного резца при втором извлечении при условии, что извлеченный в первый раз резец в ящик не возвращается.

Обозначим событие, означающее извлечение изношенного резца во втором случае. Вероятности этого события могут быть такими:

Формулы умножения вероятностей

Теорема 2.3. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:

Следствие 2.1. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:

Пример 5. Три ящика содержат по 10 деталей. В первом ящике — 8 стандартных деталей, во втором — 7, в третьем — 9. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными.

Теорема 2.4. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

Следствие 2.2. Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились.

Пример 6. В урне находятся 5 белых шаров, 4 черных и 3 синих. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его в урну. Найти вероятность того, что при первом испытании появится белый шар (событие ), при втором — черный (событие ) и при третьем — синий (событие ).

Формула полной вероятности

При этом события называются гипотезами, а вероятности — априорными. Эта формула называется формулой полной вероятности.

Пример 7. На сборочный конвейер поступают детали с трех станков. Производительность станков не одинакова. На первом станке изготовляют 50% всех деталей, на втором — 30%, на третьем — 20%. Вероятность качественной сборки при использовании детали, изготовленной на первом, втором и третьем станке, соответственно 0,98, 0,95 и 0,8, Определить вероятность того, что узел, сходящий с конвейера, качественный.

Формула Байеса

Раскрывая в этом равенстве по формуле полной вероятности (2.1), получаем

Пример 8. При условиях примера 7 рассчитать вероятности того, что в сборку попала деталь, изготовленная соответственно на первом, втором и третьем станке, если узел, сходящий с конвейера, качественный.

Решение. Рассчитаем условные вероятности по формуле Байеса:

Источник