что такое нейросеть и как она работает
Нейросети для чайников. Начало
Так получилось, что в университете тема нейросетей успешно прошла мимо моей специальности, несмотря на огромный интерес с моей стороны. Попытки самообразования несколько раз разбивались невежественным челом о несокрушимые стены цитадели науки в облике непонятных «с наскока» терминов и путанных объяснений сухим языком вузовских учебников.
В данной статье (цикле статей?) я попытаюсь осветить тему нейросетей с точки зрения человека непосвященного, простым языком, на простых примерах, раскладывая все по полочкам, а не «массив нейронов образует перцептрон, работающий по известной, зарекомендовавшей себя схеме».
Заинтересовавшихся прошу под кат.
Для чего же нужны нейросети?
Нейросеть – это обучаемая система. Она действует не только в соответствии с заданным алгоритмом и формулами, но и на основании прошлого опыта. Этакий ребенок, который с каждым разом складывает пазл, делая все меньше ошибок.
И, как принято писать у модных авторов – нейросеть состоит из нейронов.
Тут нужно сделать остановку и разобраться.
Договоримся, что нейрон – это просто некая воображаемая чёрная коробка, у которой кучка входных отверстий и одно выходное.
Причем как входящая, так и исходящая информация может быть аналоговой (чаще всего так и будет).
Как выходной сигнал формируется из кучи входных – определяет внутренний алгоритм нейрона.
Для примера напишем небольшую программу, которая будет распознавать простые изображения, скажем, буквы русского языка на растровых изображениях.
Условимся, что в исходном состоянии наша система будет иметь «пустую» память, т.е. этакий новорожденный мозг, готовый к бою.
Для того чтобы заставить его корректно работать, нам нужно будет потратить время на обучение.
Уворачиваясь от летящих в меня помидоров, скажу, что писать будем на Delphi (на момент написания статьи была под рукой). Если возникнет необходимость – помогу перевести пример на другие языки.
Также прошу легкомысленно отнестись к качеству кода – программа писалась за час, просто чтобы разобраться с темой, для серьезных задач такой код вряд ли применим.
Итак, исходя из поставленной задачи — сколько вариантов выхода может быть? Правильно, столько, сколько букв мы будем уметь определять. В алфавите их пока только 33, на том и остановимся.
Далее, определимся со входными данными.Чтобы слишком не заморачиватсья – будем подавать на вход битовый массив 30х30 в виде растрового изображения:
В итоге – нужно создать 33 нейрона, у каждого из которых будет 30х30=900 входов.
Создадим класс для нашего нейрона:
Создадим массив нейронов, по количеству букв:
Теперь вопрос – где мы будем хранить «память» нейросети, когда программа не работает?
Чтобы не углубляться в INI или, не дай бог, базы данных, я решил хранить их в тех же растровых изображениях 30х30.
Вот например, память нейрона «К» после прогона программы по разным шрифтам:
Как видно, самые насыщенные области соответствуют наиболее часто встречаемым пикселям.
Будем загружать «память» в каждый нейрон при его создании:
В начале работы необученной программы, память каждого нейрона будет белым пятном 30х30.
Распознавать нейрон будет так:
— Берем 1й пиксель
— Сравниваем его с 1м пикселем в памяти (там лежит значение 0..255)
— Сравниваем разницу с неким порогом
— Если разница меньше порога – считаем, что в данной точке буква похожа на лежащую в памяти, добавляем +1 к весу нейрона.
И так по всем пикселям.
Вес нейрона – это некоторое число (в теории до 900), которое определяется степенью сходства обработанной информации с хранимой в памяти.
В конце распознавания у нас будет набор нейронов, каждый из которых считает, что он прав на сколько-то процентов. Эти проценты – и есть вес нейрона. Чем больше вес, тем вероятнее, что именно этот нейрон прав.
Теперь будем скармливать программе произвольное изображение и пробегать каждым нейроном по нему:
Как только закончится цикл для последнего нейрона – будем выбирать из всех тот, у которого вес больше:
Именно по вот этому значению max_n, программа и скажет нам, что, по её мнению, мы ей подсунули.
По началу это будет не всегда верно, поэтому нужно сделать алгоритм обучения.
Само обновление памяти будем делать так:
Т.е. если данная точка в памяти нейрона отсутствует, но учитель говорит, что она есть в этой букве – мы её запоминаем, но не полностью, а только наполовину. С дальнейшим обучением, степень влияния данного урока будет увеличиваться.
Вот несколько итераций для буквы Г:
На этом наша программа готова.
Обучение
Начнем обучение.
Открываем изображения букв и терпеливо указываем программе на её ошибки:
Через некоторое время программа начнет стабильно определять даже не знакомые ей ранее буквы:
Заключение
Программа представляет собой один сплошной недостаток – наша нейросеть очень глупа, она не защищена от ошибок пользователя при обучении и алгоритмы распознавания просты как палка.
Зато она дает базовые знания о функционировании нейросетей.
Если данная статья заинтересует уважаемых хабравчан, то я продолжу цикл, постепенно усложняя систему, вводя дополнительные связи и веса, рассмотрю какую-нибудь из популярных архитектур нейросетей и т.д.
Поиздеваться над нашим свежерожденный интеллектом вы можете, скачав программу вместе с исходниками тут.
За сим откланяюсь, спасибо за чтение.
UPD: У нас получилась заготовка для нейросети. Пока что это ещё ей не является, но в следующей статье мы постараемся сделать из неё полноценную нейросеть.
Спасибо Shultc за замечание.
Нейросеть с нуля своими руками. Часть 1. Теория
Здравствуйте. Меня зовут Андрей, я frontend-разработчик и я хочу поговорить с вами на такую тему как нейросети. Дело в том, что ML технологии все глубже проникают в нашу жизнь, и о нейросетях сказано и написано уже очень много, но когда я захотел разобраться в этом вопросе, я понял что в интернете есть множество гайдов о том как создать нейросеть и выглядят они примерно следующим образом:
Более подробная информация разбросана кусками по всему интернету. Поэтому я постарался собрать ее воедино и изложить в этой статье. Сразу оговорюсь, что я не являюсь специалистом в области ML или биологии, поэтому местами могу быть не точным. В таком случае буду рад вашим комментариям.
Пока я писал эту статью я понял, что у меня получается довольно объемный лонгрид, поэтому решил разбить ее на несколько частей. В первой части мы поговорим о теории, во второй напишем собственную нейросеть с нуля без использования каких-либо библиотек, в третьей попробуем применить ее на практике.
Так как это моя первая публикация, появляться они будут по мере прохождения модерации, после чего я добавлю ссылки на все части. Итак, приступим.
Для чего нужны нейросети
В нашем глазу есть сенсоры, которые улавливают количество света попадающего через зрачок на заднюю поверхность глаза. Они преобразуют эту информацию в электрические импульсы и передают на прикрепленные к ним нервные окончания. Далее это сигнал проходит по всей нейронной сети, которая принимает решение о том, не опасно ли такое количество света для глаза, достаточно ли оно для того, чтобы четко распознавать визуальную информацию, и нужно ли, исходя из этих факторов, уменьшить или увеличить количество света.
На выходе этой сети находятся мышцы, отвечающие за расширение или сужение зрачка, и приводят эти механизмы в действие в зависимости от сигнала, полученного из нейросети. И таких механизмов огромное количество в теле любого живого существа, обладающего нервной системой.
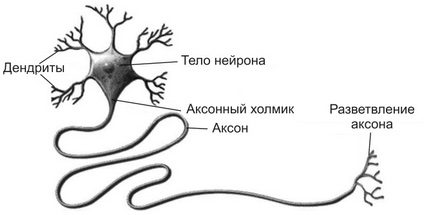
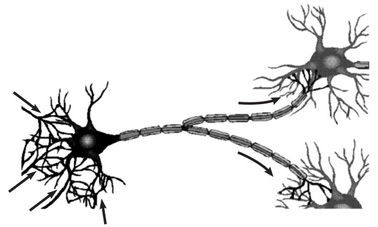
Устройство нейрона
Дендриты нейрона создают дендритное дерево, размер которого зависит от числа контактов с другими нейронами. Это своего рода входные каналы нервной клетки. Именно с их помощью нейрон получает сигналы от других нейронов.
Тело нейрона в природе, достаточно сложная штука, но именно в нем все сигналы, поступившие через дендриты объединяются, обрабатываются, и принимается решение о том передавать ли сигнал далее, и какой силы он должен быть.
Нейросети в IT
Что же, раз механизм нам понятен, почему бы нам не попробовать воспроизвести его с помощью информационных технологий?
Итак, у нас есть входной слои нейронов, которые, по сути, являются сенсорами нашей системы. Они нужны для того, чтобы получить информацию из окружающей среды и передать ее дальше в нейросеть.
Также у нас есть несколько слоев нейронов, каждый из которых получает информацию от всех нейронов предыдущего слоя, каким-то образом ее обрабатывают, и передают на следующий слой.
И, наконец, у нас есть выходные нейроны. Исходя из сигналов, поступающих от них, мы можем судить о принятом нейросетью решении.
Такой простейший вариант нейронной сети называется перцептрон, и именно его мы с вами и попробуем воссоздать.
Все нейроны по сути одинаковы, и принимают решение о том, какой силы сигнал передать далее с помощью одного и того же алгоритма. Это алгоритм называется активационной функцией. На вход она получает сумму значений входных сигналов, а на выход передает значение выходного сигнала.
Но в таком случае, получается, что все нейроны любого слоя будут получать одинаковый сигнал, и отдавать одинаковое значение. Таким образом мы могли бы заменить всю нашу сеть на один нейрон. Чтобы устранить эту проблему, мы присвоим входу каждого нейрона определенный вес. Этот вес будет обозначать насколько важен для каждого конкретного нейрона сигнал, получаемый от другого нейрона. И тут мы подходим к самому интересному.
То есть мы подаем на вход нейросети определенные данные, для которых мы знаем, каким должен быть результат. Далее мы сравниваем результат, который нам выдала нейросеть с ожидаемым результатом, вычисляем ошибку, и корректируем веса нейронов таким образом, чтобы эту ошибку минимизировать. И повторяем это действие большое количество раз для большого количества наборов входных и выходных данных, чтобы сеть поняла какие сигналы на каком нейроне ей важны больше, а какие меньше. Чем больше и разнообразнее будет набор данных для обучения, тем лучше нейросеть сможет обучиться и впоследствии давать правильный результат. Этот процесс называется обучением с учителем.
Добавим немного математики.
В качестве активационной функции нейрона может выступать любая функция, существующая на всем отрезке значений, получающихся на выходе нейрона и входных данных. Для нашего примера мы возьмем сигмоиду. Она существует на отрезке от минус бесконечности до бесконечности, плавно меняется от 0 до 1 и имеет значение 0,5 в точке 0. Идеальный кандидат. Выглядит она следующим образом:
Таким образом сумма входных значений первого нейрона скрытого слоя будет равна
Передав это значение в активационную функцию, мы получим значение, которое наш нейрон передаст далее по сети в следующий слой.
sigmoid(0,22) = 1 / (1 + e^-0,22) = 0,55
Аналогичные операции произведём для второго нейрона скрытого слоя и получим значение 0,60.
И, наконец, повторим эти операции для единственного нейрона в выходном слое нашей нейросети и получим значение 0,60, что мы условились считать как истину.
Пока что это абсолютно случайное значение, так как веса мы выбирали случайно. Но, предположим, что мы знаем ожидаемое значение для такого набора входных данных и наша сеть ошиблась. В таком случае нам нужно вычислить ошибку и изменить параметры весов, таким образом немного обучив нашу нейросеть.
Первым делом рассчитаем ошибку на выходе сети. Делается это довольно просто, нам просто нужно получить разницу полученного значения и ожидаемого.
Чтобы узнать насколько нам надо изменить веса нашего нейрона, нам нужно величину ошибки умножить на производную от нашей активационной функции в этой точке. К счастью, производная от сигмоиды довольно проста.
Таким образом наша дельта весов будет равна
Новый вес для входа нейрона рассчитывается по формуле
Аналогичным образом рассчитаем новый вес для второго входа выходного нейрона:
Итак, мы скорректировали веса для входов выходного нейрона, но чтобы рассчитать остальные, нам нужно знать ошибку для каждого из нейронов нашей нейросети. Это делается не так очевидно как для выходного нейрона, но тоже довольно просто. Чтобы получить ошибку каждого нейрона нам нужно новый вес нейронной связи умножить на дельту. Таким образом ошибка первого нейрона скрытого слоя равна:
error = 0.18 * 0.24 = 0.04
Теперь, зная ошибку для нейрона, мы можем произвести все те же самые операции, что провели ранее, и скорректировать его веса. Этот процесс называется обратным распространением ошибки.
Итак, мы знаем как работает нейрон, что такое нейронные связи в нейросети и как происходит процесс обучения. Этих знаний достаточно чтобы применить их на практике и написать простейшую нейросеть, чем мы и займемся в следующей части статьи.
Искусственные нейронные сети простыми словами
Когда, за бутылкой пива, я заводил разговор о нейронных сетях — люди обычно начинали боязливо на меня смотреть, грустнели, иногда у них начинал дёргаться глаз, а в крайних случаях они залезали под стол. Но, на самом деле, эти сети просты и интуитивны. Да-да, именно так! И, позвольте, я вам это докажу!
Допустим, я знаю о девушке две вещи — симпатична она мне или нет, а также, есть ли о чём мне с ней поговорить. Если есть, то будем считать это единицей, если нет, то — нулём. Аналогичный принцип возьмем и для внешности. Вопрос: “В какую девушку я влюблюсь и почему?”
Можно подумать просто и бескомпромиссно: “Если симпатична и есть о чём поговорить, то влюблюсь. Если ни то и ни другое, то — увольте.”
Но что если дама мне симпатична, но с ней не о чем разговаривать? Или наоборот?
Понятно, что для каждого из нас что-то одно будет важнее. Точнее, у каждого параметра есть его уровень важности, или вернее сказать — вес. Если помножить параметр на его вес, то получится соответственно “влияние внешности” и “влияние болтливости разговора”.
И вот теперь я с чистой совестью могу ответить на свой вопрос:
“Если влияние харизмы и влияние болтливости в сумме больше значения “влюбчивость” то влюблюсь…”
То есть, если я поставлю большой вес “болтологичности” дамы и маленький вес внешности, то в спорной ситуации я влюблюсь в особу, с которой приятно поболтать. И наоборот.
Собственно, это правило и есть нейрон.
Искусственный нейрон — это такая функция, которая преобразует несколько входных фактов в один выходной. Настройкой весов этих фактов, а также порога возбуждения — мы настраиваем адекватность нейрона. В принципе, для многих наука жизни заканчивается на этом уровне, но ведь эта история не про нас, верно?
Сделаем ещё несколько выводов:
Смешно, но параметр “влюбчивости” называется “порогом возбуждения”. Но, дабы эта статья не получила рейтинг “18+”, давайте договоримся говорить просто “порог”, ок?
Нейронная сеть
Не бывает однозначно симпатичных и однозначно общительных дам. Да и влюблённость влюблённости рознь, кто бы что ни говорил. Потому давайте вместо брутальных и бескомпромиссных “0” и “1”, будем использовать проценты. Тогда можно сказать — “я сильно влюблён (80%), или “эта дама не особо разговорчива (20%)”.
Наш примитивный “нейрон-максималист” из первой части уже нам не подходит. Ему на смену приходит “нейрон-мудрец”, результатом работы которого будет число от 0 до 1, в зависимости от входных данных.
“Нейрон-мудрец” может нам сказать: “эта дама достаточно красива, но я не знаю о чём с ней говорить, поэтому я не очень-то ей и восхищён”
К слову говоря, входные факты нейрона называются синапсами, а выходное суждение — аксоном. Связи с положительным весом называются возбуждающими, а с отрицательным — тормозящими. Если же вес равен нулю, то считается, что связи нет (мёртвая связь).
Поехали дальше. Сделаем по этим двум фактам другую оценку: насколько хорошо с такой девушкой работать (сотрудничать)? Будем действовать абсолютно аналогичным образом — добавим мудрый нейрон и настроим веса комфортным для нас образом.
Но, судить девушку по двум характеристикам — это очень грубо. Давайте судить её по трём! Добавим ещё один факт – деньги. Который будет варьироваться от нуля (абсолютно бедная) до единицы (дочь Рокфеллера). Посмотрим, как с приходом денег изменятся наши суждения….
Для себя я решил, что, в плане очарования, деньги не очень важны, но шикарный вид всё же может на меня повлиять, потому вес денег я сделаю маленьким, но положительным.
В работе мне абсолютно всё равно, сколько денег у девушки, поэтому вес сделаю равным нулю.
Оценивать девушку только для работы и влюблённости — очень глупо. Давайте добавим, насколько с ней будет приятно путешествовать:
Соединим все эти три схемы в одну и обнаружим, что мы перешли на более глубокий уровень суждений, а именно: от харизмы, денег и разговорчивости — к восхищению, сотрудничеству и комфортности совместного путешествия. И заметьте — это тоже сигналы от нуля до единицы. А значит, теперь я могу добавить финальный “нейрон-максималист”, и пускай он однозначно ответит на вопрос — “жениться или нет”?
Ладно, конечно же, не всё так просто (в плане женщин). Привнесём немного драматизма и реальности в наш простой и радужный мир. Во-первых, сделаем нейрон «женюсь — не женюсь» — мудрым. Сомнения же присущи всем, так или иначе. И ещё — добавим нейрон «хочу от неё детей» и, чтобы совсем по правде, нейрон “держись от неё подальше».
Я ничего не понимаю в женщинах, и поэтому моя примитивная сеть теперь выглядит как картинка в начале статьи.
Входные суждения называются “входной слой”, итоговые — “выходной слой”, а тот, что скрывается посередине, называется «скрытым». Скрытый слой — это мои суждения, полуфабрикаты, мысли, о которых никто не знает. Скрытых слоёв может быть несколько, а может быть и ни одного.
Долой максимализм.
Помните, я говорил об отрицательном влияние денег на моё желание путешествовать с человеком? Так вот — я слукавил. Для путешествий лучше всего подходит персона, у которой денег не мало, и не много. Мне так интереснее и не буду объяснять почему.
Но тут я сталкиваюсь с проблемой:
Если я ставлю вес денег отрицательным, то чем меньше денег — тем лучше для путешествий.
Если положительным, то чем богаче — тем лучше,
Если ноль — тогда деньги “побоку”.
Чтобы это обойти, я сделаю два нейрона — “денег много” и “денег мало”, и подам им на вход денежный поток от нашей дамы.
Теперь у меня есть два суждения: “много” и “мало”. Если оба вывода незначительны, то буквально получится “ни много — ни мало”. То есть, добавим на выход ещё один нейрон, с отрицательными весами:
“Нимногонимало”. Красные стрелки — положительные связи, синие — отрицательные
Вообще, это значит, что нейроны подобны элементам конструктора. Подобно тому, как процессор делают из транзисторов, мы можем собрать из нейронов мозг. Например, суждение “Или богата, или умна” можно сделать так:
Или-или. Красные стрелки — положительные связи, синие – отрицательные
можно заменить “мудрые” нейроны на “максималистов” и тогда получим логический оператор XOR. Главное — не забыть настроить пороги возбуждения.
В отличие от транзисторов и бескомпромиссной логики типичного программиста “если — то”, нейронная сеть умеет принимать взвешенные решения. Их результаты будут плавно меняться, при плавном изменение входных параметров. Вот она мудрость!
Обращу ваше внимание, что добавление слоя из двух нейронов, позволило нейрону “ни много — ни мало” делать более сложное и взвешенное суждение, перейти на новый уровень логики. От “много” или “мало” — к компромиссному решению, к более глубокому, с философской точки зрения, суждению. А что если добавить скрытых слоёв ещё? Мы способны охватить разумом ту простую сеть, но как насчёт сети, у которой есть 7 слоёв? Способны ли мы осознать глубину её суждений? А если в каждом из них, включая входной, около тысячи нейронов? Как вы думаете, на что она способна?
Представьте, что я и дальше усложнял свой пример с женитьбой и влюблённостью, и пришёл к такой сети. Где-то там в ней скрыты все наши девять нейрончиков, и это уже больше похоже на правду. При всём желании, понять все зависимости и глубину суждений такой сети — попросту невозможно. Для меня переход от сети 3х3 к 7х1000 — сравним с осознанием масштабов, если не вселенной, то галактики — относительно моего роста. Попросту говоря, у меня это не получится. Решение такой сети, загоревшийся выход одного из её нейронов — будет необъясним логикой. Это то, что в быту мы можем назвать “интуицией” (по крайней мере – “одно из..”). Непонятное желание системы или её подсказка.
Но, в отличие от нашего синтетического примера 3х3, где каждый нейрон скрытого слоя достаточно чётко формализован, в настоящей сети это не обязательно так. В хорошо настроенной сети, чей размер не избыточен для решения поставленной задачи — каждый нейрон будет детектировать какой-то признак, но это абсолютно не значит, что в нашем языке найдётся слово или предложение, которое сможет его описать. Если проецировать на человека, то это — какая-то его характеристика, которую ты чувствуешь, но словами объяснить не можешь.
Обучение.
Несколькими строчками ранее я обмолвился о хорошо настроенной сети, чем вероятно спровоцировал немой вопрос: “А как мы можем настроить сеть, состоящую из нескольких тысяч нейронов? Сколько “человеколет” и погубленных жизней нужно на это. Боюсь предположить ответ на последний вопрос. Куда лучше автоматизировать такой процесс настройки — заставить сеть саму настраивать себя. Такой процесс автоматизации называется обучением. И чтобы дать поверхностное о нём представление, я вернусь к изначальной метафоре об “очень важном вопросе”:
Мы появляемся в этом мире с чистым, невинным мозгом и нейронной сетью, абсолютно не настроенной относительно дам. Её необходимо как-то грамотно настроить, дабы счастье и радость пришли в наш дом. Для этого нам нужен некоторый опыт, и тут есть несколько путей по его добыче:
1) Обучение с учителем (для романтиков). Насмотреться на голливудские мелодрамы и начитаться слезливых романов. Или же насмотреться на своих родителей и/или друзей. После этого, в зависимости от выборки, отправиться проверять полученные знания. После неудачной попытки — повторить всё заново, начиная с романов.
2) Обучение без учителя (для отчаянных экспериментаторов). Попробовать методом “тыка” жениться на десятке-другом женщин. После каждой женитьбы, в недоумение чесать репу. Повторять, пока не поймёшь, что надоело, и ты “уже знаешь, как это бывает”.
3) Обучение без учителя, вариант 2 (путь отчаянных оптимистов). Забить на всё, что-то делать по жизни, и однажды обнаружить себя женатым. После этого, перенастроить свою сеть в соответствие с текущей реальностью, дабы всё устраивало.
Далее, по логике я должен расписать всё это подробно, но без математики это будет слишком философично. Потому считаю, что мне стоит на этом остановиться. Быть может в другой раз?
Всё вышесказанное справедливо для искусственной нейронной сети типа “персептрон”. Остальные сети похожи на нее по основным принципам, но имеют свою нюансы.
Хороших вам весов и отличных обучающих выборок! Ну а если это уже и не нужно, то расскажите об этом кому-нибудь ещё.