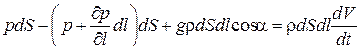что такое неустановившееся движение жидкости

Установившееся и неустановившееся движение.

Установившимся называют такое движение жидкости, при ко­тором скорость потока и давление в любой его точке не изменяются с течением времени и зависят только от ее положения в потоке, т. е. являются функциями ее координат. Примерами установившегося движения могут служить истечение жидкости из отверстия резервуара при постоянном напоре, а также поток воды в канале при не­изменном его сечении и постоянной глубине.

Неустановившимся называют такое движение жидкости, при ко­тором скорость движения и давление в каждой данной точке изме­няются с течением времени, т. е. являются функциями не только координат, но и времени. Примером неустановившегося движения служит истечении жидкости из отверстия резервуара при перемен­ном напоре. В этом случае в каждой точке сечения струи, выте­кающей из отверстия, скорость движения и давление изменяются во времени.

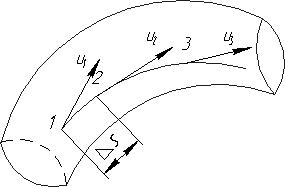
Линия тока. В точках 1, 2, 3 и т. д. потока, взятых на расстоя­нии ΔS друг от друга, проведем векторы u₁, u₂, u₃, показывающие значение и направление скоростей движения частиц жидкости в данный момент времени (рис. 1.18). Получим ломаную линию 1—2— 3и т. д. Если уменьшить длину от­резков ΔS, то в пределе ломаная линия станет кривой.

Рис. 1.18. Схематическое изображение линии тока в потоке

Эта кривая, называемая линией тока, характеризуется тем, что в данный момент времени во всех ее точках векторы скоростей бу­дут касательными к ней.

Элементарная струнка. Если в движущейся жидкости выделить бесконечно малый замкнутый контур и через все его точки провести линии тока, соответствующие данному моменту времени, получится как бы трубчатая непроницаемая поверхность, называемая трубкой тока.

Масса жидкости, движущейся внутри трубки тока, образует элементарную струйку.

Поток. Совокупность элементарных струек, представляющая собой непрерывную массу частиц, движущихся но какому-либо направлению, образует поток жидкости. Поток может быть пол­ностью или частично ограничен твердыми стенками, например в трубопроводе или канале, и может быть свободным, например струя, выходящая из сопла гидромонитора.

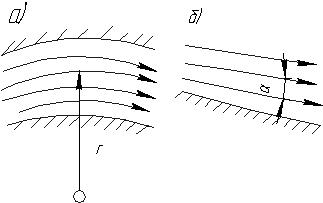
Рис. 1.19. Условия плавно из­меняющегося движения

Равномерным называют такое уста­новившееся движение жидкости, при котором живые сечения и средняя скорость потока не меняются по его длине. Примером равномерного дви­жения служит движение жидкости в цилиндрической трубе или в кана­ле неизменного сечения и постоянной глубины.

Неравномерным называют такое установившееся движение жид­кости, при котором живые сечения и средние скорости потока из­меняются по его длине. Примером неравномерного движения служит движение жидкости в конической трубе, в естественном русле, на перепаде.

При равномерном движении липни тока представляют собой систему прямых параллельных линий. Такое движение называется также параллельно–струйным. При движении жидкости в естествен­ных руслах живое сечение обычно непрерывно изменяется вдоль по­тока как по форме, так и по площади, и движение жидкости являет­ся установившимся неравномерным. Для облегчения изучения та­кого движения в гидравлике введено понятие плавно изменяюще­гося движения, которое характеризуется следующими свойствами (рис. 1.19):

Последнее свойство просто обосновывается. Если внутри плавно изменяющегося потока выделить частицу жидкости и спроекти­ровать все действующие на нее силы па плоскость живого сечения, то вследствие того, что скорости и ускорения почти перпендикуляр­ны живому сечению, силы инерции в уравнение равновесия не войдут; в связи с этим уравнение равновесия и закон распределения давления в плоскости живого сечения не будут отличаться от закона распределения давления в жидкости, находящейся в покое.

Напорным называется поток, у которого но всему периметру живого сечения жидкость соприкасается с твердыми стенками. Примером напорного потока может служить движение воды в водо­проводных трубах.

Безнапорным называется поток со свободной поверхностью. Примером безнапорного потока служит движение воды в реках, каналах и канализационных трубах.

1. В механике сплошной среды применяются два метода исследования – метод Л. Эйлера и метод Лагранжа.

В методе Л.Эйлера рассчитываются параметры сплошной среды в одних и тех же неподвижных точках пространства. Этот метод чаще всего используется в гидромеханике. Здесь данные расчета легко сравнивать с результатами экспериментов, т.к. все датчики (давления, температуры, скорости и т.п.) устанавливаются в неподвижных точках (труб, воздуховодов и т.п.).

В методе Лагранжа рассчитываются параметры (скорость, давление, температура) в одних и тех же подвижных точках среды. Метод Лагранжа более сложный. Он используется в научных исследованиях и в теории упругости. Здесь рассчитываются траектории частиц, т.к. здесь важно рассчитать перемещение точек тела. Здесь датчики параметров перемещаются вместе с точками твердого тела.

Источник

НЕУСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ ЖИДКОСТИ В ТРУБАХ

В практике эксплуатации систем водоснабжения и водоотведения достаточно часто встречаются случаи неустановившегося движения потоков. Неустановившееся движение наблюдается как в напорных трубах, так и в открытых руслах.

В напорных трубах поток жидкости ограничен жесткими стенками. Площадь живого сечения потока не зависит от времени и может являться функцией расстояния вдоль трубы, т.е. . На расход Q расстояние не влияет. Расход жидкости зависит от времени, т.е. . Однако скорость связана с площадью сечения, следовательно, .

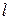
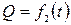
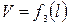
Средняя скорость потока для данного момента времени

.

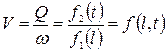
Для получения уравнения, описывающего изменения гидродинамических характеристик потоков при неустановившемся движении, используется уравнение неустановившегося движения для элементарной струйки несжимаемой жидкости.

Уравнение неустановившегося движения для элементарной струйки вязкой несжимаемой жидкости записывается в виде уравнения Бернулли для двух живых сечений 1-1 и 2-2:

, (5.45)

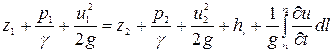
где 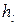— потери напора по длине струйки между сечениями.

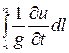
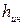
Интеграл по аналогии с другими слагаемыми уравнения Бернулли называют инерционным напором .

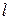
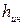
При неустановившемся движении жидкости в трубах на определенном участке длиной также учитывается инерционный напор .

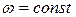
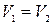
В цилиндрической трубе площадь сечения по длине потока, средние скорости и для рассматриваемого момента времени.

Потери напора по длине на участке от сечения 1-1 до сечения 2-2 определяются по формуле Дарси-Вейсбаха:

.

Ускорение 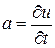постоянно по длине участка трубы; следовательно, инерционный напор

. (5.46)

Уравнение неустановившегося движения в трубе согласно (5.45)

. (5.47)

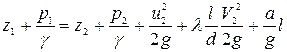
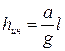
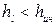
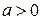
Подобно потерям напора, инерционный напор влияет на значение полной удельной энергии во втором сечении. Величина и знак инерционного напора зависят от значения и направления ускорения потока. При замедляющемся движении ( ) инерционный напор будет отрицательным, т.е. на пути между расчетными сечениями будет высвобождаться кинетическая энергия; и если потери напора по длине на этом участке будут невелики ( ), то полный напор для данного момента времени между расчетными сечениями будет возрастать. При положительном ускорении потока ( ) за тот же промежуток времени между сечениями удельная энергия жидкости уменьшается.

Дата добавления: 2015-12-29 ; просмотров: 724 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Гидродинамика. Характер изменения поля скоростей.

По характеру изменения поля скоростей во времени движения жидкости выделяют установившиеся и неустановившиеся, квазистационарное.

Установившееся движение – движение, характеризующееся тем, что в любом месте потока жидкости скорость (и давление) с течением времени претерпевают изменения, имеется в виду, что указанные показатели зависят исключительно от координат точки. Их величина изменяется лишь при переходе к другой точке пространства:

Неустановившееся движение – движение, характеризующееся тем, что в любом месте потока жидкости скорость с течением времени претерпевает изменения, т. е. выступает как функция координат и времени:

Квазистационарное движение – движение, характеризующееся тем, что изменчивость характеристик движения жидкости в течение отобранного временного отрезка не будет существенной, имеется в виду, что ее влияние лежит в пределах допускаемой точности решения, и его можно рассматривать как установившееся.

При описании установившегося движения жидкости выделяют равномерное и неравномерное.

Равномерным принято обозначать установившееся движение, при котором живые сечения вдоль потока неизменны: в этом случае w = const; средние скорости по длине потока также неизменны, т.е. v = const.

Установившееся движение принято обозначать неравномерным, когда выполняется условие, что распределение скоростей в различных поперечных сечениях разное; при этом средняя скорость и площадь поперечного сечения потока могут пребывать и постоянными вдоль потока.

Источник

Неустановившееся движение жидкости в жестких трубах

Как отмечалось ранее, неустановившимся (нестационарным) движением жидкости называется движение, переменное во времени. При таком движении и вектор скорости, и давление являются функциями не только координат точки, но и времени, то есть .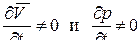

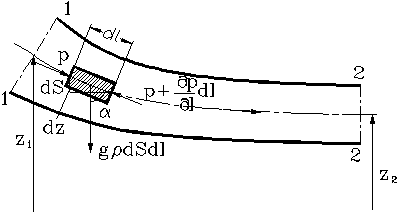
Выделим в потоке идеальной несжимаемой жидкости элемент струйки длиной dl и площадью сечения dS (Рис. 42). Запишем для этого элемента струйки уравнение второго закона Ньютона в проекции на направление касательной к осевой линии струйки.

Рис. 42. Схема для вывода уравнения неустановившегося течения

.

В выражении использована частная производная от давления p потому, что оно, как и скорость V, является функцией двух переменных – l и t, а уравнение записано для определенного момента времени. В правой части уравнения записана полная производная от скорости по времени, то есть ускорение, которое равно сумме локального (местного) ускорения, обусловленного нестационарностью движения, и конвективного ускорения, определяемого геометрией потока, то есть

.

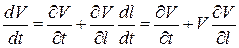
Учитывая, что cos a = – дz/дl, где z – вертикальная координата, перепишем уравнение движения в виде

.

Интегрируя вдоль струйки от сечения 1 – 1 до сечения 2 – 2 в тот же фиксированный момент времени, получаем

,

.

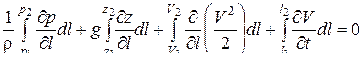
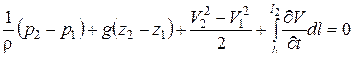
Разделим уравнение на g и перегруппируем члены:

.

Полученное уравнение отличается от уравнения Бернулли только последним слагаемым в правой части, которое называется инерционным напором:

.

Из уравнения ясен смысл инерционного напора – это разность полных напоров в сечениях 1 – 1 и 2 – 2 в данный фиксированный момент времени, обусловленная ускорением или торможением потока жидкости.

Для неустановившегося потока реальной жидкости необходимо учесть неравномерность распределения скоростей по сечению потока и потери напора. Следовательно, уравнение примет вид:

.

Для трубы постоянного диаметра локальное ускорение также постоянно вдоль трубы, поэтому инерционный напор

.

Если трубопровод состоит из нескольких участков с сечениями разных площадей S₁, S₂ и т.д. (или трубопровод присоединен к цилиндру, в котором ускоренно движется поршень), то инерционный напор для всего трубопровода определяется как сумма инерционных напоров всех отдельных участков. При этом ускорения на отдельных участках определяются из уравнения, полученного дифференцированием уравнения расхода по времени:

В уравнение неустановившегося движения жидкости в этом случае надо подставить

Инерционный напор записывается в правую часть уравнения, причем его знак совпадает со знаком ускорения a. То есть при положительном ускорении инерционный напор положителен и уменьшает полный напор подобно потерям напора на местных и линейных сопротивлениях. Но инерционный напор нельзя рассматривать как безвозвратные потери, так как при торможении потока он меняет знак и увеличивает полный напор вдоль потока, то есть его действие противоположно действию гидравлических сопротивлений. Полученное уравнение относится лишь к определенному моменту времени или к равноускоренному движению жидкости. Если же ускорение непрерывно изменяется, то и инерционный напор будет непрерывно изменяться, изменяя во времени распределение напоров вдоль потока.

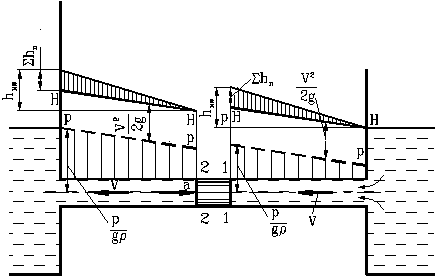
В качестве примера на Рис. 43 показана труба постоянного сечения, соединяющая два резервуара. В трубе возвратно-поступательно движется поршень. На Рис. 43а поршень движется справа налево со скоростью V и ускорением a. С таким же ускорением движется и жидкость в трубе. Для каждого участка трубы – всасывающего (до поршня) и напорного (за поршнем) – показаны линии изменения полного напора H – H, пьезометрических напоров p – p, а также потерь напора Sh_п и инерционного напора h_ин в некоторый фиксированный момент времени.

Из рисунка видно, что инерционный напор способствует снижению давления и даже приводит к возникновению разрежения за поршнем и вызывает более значительное повышение давления перед поршнем по сравнению с установившимся движением.

На Рис. 43б показаны те же линии, но в момент, когда поршень движется с той же скоростью в том же направлении, но с отрицательным ускорением, то есть тормозится. В этом случае инерционный напор изменяет свой знак, компенсирует гидравлические потери, и гидравлический уклон также меняет свой знак на обратный.

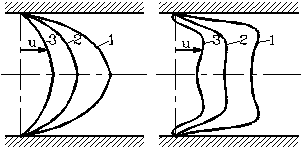
Гидравлические потери при неустановившемся движении в общем случае отличны от потерь при установившемся движении. Это связано с изменением профиля скоростей по сечению трубы. Так при ускоренном движении профиль становится более полным (Рис.44), и коэффициент Кориолиса a уменьшается, а при замедленном – более вытянутым, и a растет. На Рис. 44 показано изменение распределения скоростей по сечению потока при ускоренном ламинарном движении жидкости при трех значениях расхода ( Рис. 44а – при равномерном движении, б – при ускорен-

Рис. 43. Построение пьезометрических линий и линий полного напора

ном). Как видно из рисунка, в некоторых случаях в пристенном слое потока могут возникать даже противотоки.

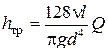
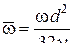
В случае ламинарного течения с гармоническим изменением расхода по времени в закон Пуазейля, отражающий потери на трение по длине , надо ввести поправочный коэффициент k, который является функцией круговой частоты , где w – угловая частота колебаний жидкости с вязкостью n в трубе диаметром d.

Рис. 44. Изменение профиля эпюры скоростей

при ускоренном ламинарном течении

Поправочный коэффициент находится по формуле:

.

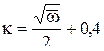
При увеличении частоты возрастание гидравлических потерь может быть весьма существенным, причем различие между гидравлическими потерями при ламинарном и турбулентном режимах течения уменьшается.

Источник

Виды движения жидкости. Неустановившееся и установившееся движение

Неустановившееся и установившееся движение

Величины гидродинамических давлений p и скоростей u в потоке жидкости в общем случае распределены неравномерно, они меняются при переходе от одной точки потока к другой, т.е. являются функциями координат (x, y, z).

Помимо того гидродинамические давления и скорости в одних и тех же фиксированных точках потока могут изменяться во времени как по величине, так и по направлению. Эти условия в общем виде могут быть записаны следующим образом:

Такой вид движения, при котором гидродинамические давления и скорости в каждой точке потока жидкости изменяются во времени по величине и направлению, называется неустановившимся движением.

Примерами неустановившегося движения жидкости могут служить:

— движение воды в реке во время весеннего половодья или при разрушении плотины, сопровождающееся изменением во времени уровня воды, ширины потока, скорости течения и давления в каждом сечении потока;

— истечение жидкости через отверстие в резервуаре при переменном уровне жидкости в нем, когда траектория струи и скорости истечения жидкости изменяются во времени;

— движение перекачиваемой жидкости во всасывающем или нагнетательном трубопроводе поршневого насоса.

Неустановившееся движение является самым общим и самым сложным видом движения жидкости, изучению которого посвящаются специальные курсы гидравлики.

Мы будем, в основном, рассматривать вопросы, касающиеся установившегося движения жидкости, при котором скорости и гидродинамические давления в каждой точке потока не изменяются во времени, а являются лишь функциями координат. При установившемся движении

Эти зависимости можно пояснить следующим образом. Пусть в данной фиксированной точке потока с координатами x, y, z в какой-то момент времени t частица жидкости будет обладать скоростью u (с проекциями на координатные оси u_x, u_y, u_z) и испытывать гидродинамическое давление p. Спустя некоторое время dt рассматриваемая частица переместится в какую-то другую точку, может приобрести другую скорость и испытывать другое давление. Но вторая частица жидкости, пришедшая на смену первой в фиксированную точку потока с координатами x, y, z будет обладать в точности такой же скоростью по величине и направлению и испытывать абсолютно такое же гидродинамическое давление, что и первая частица, когда она находилась в данной точке.

Следовательно, для полной характеристики установиваегося движения жидкости необходимо уметь находить функции (В – 3), которые будучи выражены в аналитической форме позволяют определить четыре неизвестных величины p, u_x, u_y, u_z в пространстве x, y, z.

Примерами установившегося движения жидкости являются:

— движение жидкости ( воды, бензина, масла ) в трубопроводе с постоянной скоростью течения;

— движение воды в канале постоянного сечения при постоянной глубине воды ;

— истечение жидкости через отверстие в резервуаре при постоянном уровне жидкости.

Источник