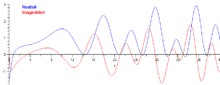
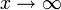что такое нетривиальные нули дзета функции
Закономерности простых чисел. Гипотеза Римана
 |
В 1859 году немецкий математик Бернхард Риман взял давнюю идею Эйлера и развил ее совершенно по-новому, определив так называемую дзета-функцию. Одним из результатов этой работы стала точная формула для количества простых чисел до заданного предела. Формула представляла собой бесконечную сумму, но специалистам по анализу к этому не привыкать. И это не было бесполезной игрой ума: благодаря этой формуле удалось получить новые подлинные знания о мире простых чисел. Мешала только одна маленькая неувязка. Хотя Риман мог доказать, что его формула точна, самые важные потенциальные следствия из нее полностью зависели от одного простого утверждения, касающегося дзета-функции, и вот это то простое утверждение Риман никак не мог доказать. И сегодня, полтора столетия спустя, мы все еще не сумели сделать это. Сегодня это утверждение называется гипотезой Римана и представляет собой, по сути, священный Грааль чистой математики.
Теорема о распределении простых чисел была ответом на евклидову теорему о том, что простые числа уходят в бесконечность и могут быть сколь угодно большими. Другая фундаментальная евклидова теорема говорит о единственности разложения на простые множители: каждое положительное целое число есть произведение простых чисел, причем только одного их набора. В 1737 году Эйлер понял, что первую теорему можно переформулировать в виде поразительной формулы из действительного анализа, и тогда второе утверждение становится простым следствием этой формулы. Для начала я представлю формулу, а затем попытаюсь разобраться в ней. Вот она:
Здесь принимает все простые значения, а — константа. Эйлера интересовал в основном случай, при котором — целое число, но его формула работает и для действительных чисел, в случае если больше единицы. Это условие необходимо для того, чтобы ряд в правой части сошелся, т. е., будучи продолжен до бесконечности, принял бы осмысленное значение.
Это необыкновенная формула. В левой части мы перемножаем бесконечно много выражений, которые зависят только от простых чисел. В правой — складываем бесконечное число выражений, которые зависят от всех положительных целых чисел. Эта формула выражает, на языке анализа, некоторое отношение между целыми и простыми числами. Главное отношение такого рода — это единственность разложения на простые множители, именно она оправдывает существование формулы.
поэтому взвешенный подсчет дает
Воспользовавшись методами анализа, информацию об этом более хитроумном способе подсчета простых чисел можно превратить в информацию об обычном способе. Однако этот метод приводит к более простым формулам, и присутствие логарифма — не слишком дорогая цена за это. В этих терминах точная формула Римана говорит о том, что взвешенный подсчет до предела эквивалентен
Это заявление о кси-функции эквивалентно аналогичному заявлению о зависимой от нее дзета-функции. А именно: все нетривиальные нули дзета-функции представляют собой комплексные числа вида: они лежат на критической линии «действительная часть равна » (см. рис.). Эта версия замечания и есть знаменитая гипотеза Римана.
 |
Замечание Римана звучит достаточно небрежно, как будто высказано между делом и эта гипотеза не имеет особого значения. И это действительно так, если говорить только о программе Римана по доказательству теоремы о распределении простых чисел. Но во многих других вопросах верно обратное. Многие считают гипотезу Римана важнейшим из остающихся на сегодняшний день открытыми математических вопросов.
Риман так и не довел свою программу до логического конца. Более того, он никогда больше ничего не писал по этому вопросу.
Но два других математика, приняв у него эстафету, показали, что догадка Римана верна. В 1896 году Жак Адамар и Шарль-Жан де ла Валле Пуссен независимо друг от друга вывели теорему о распределении простых чисел, доказав, что все нетривиальные нули дзета-функции лежат в пределах критической полосы. Доказательства у обоих получились очень сложными и техничными, но тем не менее свою задачу они выполнили. Возникла новая мощная область математики — аналитическая теория чисел. Применение ей нашлось в самых разных уголках теории чисел: с ее помощью решали давние задачи и выявляли новые закономерности. Другие математики позже нашли несколько более простых доказательств теоремы о числе простых, а Атле Сельберг и Пал Эрдеш открыли даже очень сложное доказательство, вовсе не требовавшее применения комплексного анализа. Но к тому моменту при помощи идеи Римана было доказано бесчисленное множество важных теорем, включая аппроксимации многих функций теории чисел. Так что это новое доказательство хоть и добавило в эту историю каплю иронии, но ни на что, в сущности, не повлияло. В 1980 году Дональд Ньюман нашел гораздо более простое доказательство, для которого достаточно оказалось всего лишь одной из самых базовых теорем комплексного анализа — теоремы Коши.
Хотя Риман объявил свою гипотезу ненужной для достижения ближайших целей, оказалось, что она жизненно необходима для разрешения многих других вопросов теории чисел. Прежде чем обсуждать гипотезу Римана, нам стоит взглянуть на некоторые теоремы, которые — если бы гипотеза была доказана — из нее следуют.
Из гипотезы Римана можно получить немало других оценок для функций теории чисел. К примеру, из нее прямо следует, что сумма делителей меньше
Но подлинное значение гипотезы Римана куда глубже. Существуют далеко идущие обобщения и сильное подозрение, что тот, кто сумеет доказать гипотезу Римана, сможет, вероятно, доказать и связанную с ней обобщенную гипотезу Римана. А это, в свою очередь, даст математикам власть над обширными областями теории чисел.
Прочерки указывают на то, что соответствующее число не простое.
Доказать, что простых чисел вида тоже бесконечно много, гораздо сложнее, — это можно сделать, но лишь при помощи некоторых достаточно сложных теорем. Разница в подходах обусловлена тем, что любое число вида имеет делитель того же вида, а в отношении чисел вида это не всегда верно.
Кстати говоря, на любой из подобных вопросов нетрудно выдвинуть разумное предположение — простые числа в арифметической последовательности. Случай с достаточно типичен. Эксперимент быстро показывает, что числа приведенных выше четырех видов имеют примерно равные шансы оказаться простыми. Вот похожая таблица:
Так что должно существовать бесконечное количество простых чисел каждого вида, и в среднем к каждому виду должна относиться четверть всех простых чисел до заданного предела.
Для римановой дзета-функции важен не только ряд, но и его аналитическое продолжение, придающее функции значения во всех комплексных точках.
Имеется множество косвенных свидетельств того, что гипотеза Римана — как оригинальная, так и обобщенная — справедлива. Много хорошего следовало бы из истинности этих гипотез. Ни одно из этих следствий за все время не удалось опровергнуть, а ведь сделать это — то же самое, что опровергнуть гипотезу Римана. Но ни доказательства, ни опровержения пока нет. Широко распространено мнение, что доказательство оригинальной гипотезы Римана открыло бы дорогу и к доказательству обобщенного ее варианта. Но на самом деле, возможно, лучше было бы атаковать сразу обобщенную гипотезу Римана во всей ее грозной красе — воспользоваться всем арсеналом доступных на сегодняшний день методов, доказать, а затем вывести оригинальную гипотезу Римана как ее частный случай.
Сегодня у исследователей появился новый стимул к борьбе за доказательство гипотезы Римана: крупный приз.
Многие представители математической науки считают правильным, что в их области не присуждается Нобелевская премия. В настоящее время она составляет чуть больше миллиона долларов, а такая сумма легко может исказить цели исследователей и породить споры о приоритетах. Однако отсутствие крупной математической премии также может исказить представления общества о значимости и полезности этой науки. Можно подумать, что открытия, за которые никто не хочет платить, не так уж важны. Возможно, поэтому не так давно появились две очень престижные новые математические премии. Одна из них — Абелевская — присуждается ежегодно Норвежской академией науки и словесности и названа в честь великого норвежского математика Нильса Хенрика Абеля. Вторая награда — это премии за решение семи «проблем тысячелетия», объявленные Математическим институтом Клэя. Этот институт основали в 1998 году в Кембридже (штат Массачусетс) американский бизнесмен Лэндон Клэй и его жена Лавиния. Лэндон Клэй активно занимается паевыми инвестиционными фондами и при этом любит и уважает математику. Его организация проводит встречи, выделяет гранты на исследования, организует публичные лекции и присуждает ежегодную премию за математические исследования.
Стоит также помнить о том, что гипотезы, даже освященные временем, иногда оказываются ошибочными. Сегодня большинство математиков, судя по всему, считает, что когда-нибудь гипотеза Римана будет доказана. Некоторые, однако, думают, что она, возможно, все-таки неверна, и где-то в дебрях очень больших чисел может скрываться нуль дзета-функции, который не лежит на критической линии. Если такой «контрпример» существует, то он, скорее всего, окажется очень-очень большим.
Однако на переднем крае математики просто мнение стоит немного. Интуиция зачастую очень помогает ученым, но известно немало случаев, когда это замечательное чувство ошибалось. Житейский здравый смысл может лгать, оставаясь при этом и общепризнанным, и здравым. Литтлвуд, один из лучших знатоков комплексного анализа, выразился вполне однозначно: в 1962 году он сказал, что уверен в ошибочности гипотезы Римана, и добавил, что нет никаких мыслимых причин, по которым она была бы верна. Кто прав? Поживем, увидим.
Иэн Стюарт
Emeritus Professor of Mathematics at the University of Warwick, England
Буддийский физмат: как гёделевская неполнота и иррациональные числа породили нашу Вселенную
Каждый человек в определенный момент своей жизни начинает задаваться вопросами: «Почему существует Вселенная?», «Что такое время?», «Что было до Большого Взрыва?».
Со мной это произошло несколько лет тому назад. Я стал искать ответы на эти вопросы, пытаясь найти их везде: в научно-популярных книгах по физике, в древнегреческой и древнеиндийской философии, в популярных и эзотерических религиях. В каждом из этих направлений человеческой мысли я не находил окончательной истины, но находил одну из её бесконечных граней.
Наш ум анализирует поток сырых сенсорных данных от органов чувств: он различает разные цвета, звуки, запахи и конструирует из них цельную картину сознания. Именно из-за этих базовых свойств нашего ума: различения базовых частиц восприятия и конструирования из них абстракций, мы видим внешний мир как набор отношений между абстрактными объектами.
Пустота материи, пространства и времени
Если мы рассмотрим любые предметы, которые мы считаем материальными, с точки зрения буддийской доктрины пустоты, то они окажутся иллюзией и «исчезнут». Виктор Пелевин в своём известном романе «Чапаев и Пустота» рассказывал метафорическую историю про Будду, указывавшего на разные предметы своим мизинцем, после чего эти предметы тотчас исчезали.
Наука о пустоте
Вот её определение из Википедии:
Если однажды мы встретимся с представителями внеземных цивилизаций, то можно с уверенностью сказать, что и в их математическом аппарате дважды два будет равно четырем. Конечно, они будут обозначать цифры и операции другими символами, но суть будет та же самая. С помощью математических выражений мы сможем найти и другие сходства с инопланетной наукой: у них ведь будут те же самые, что и у нас, законы физики, химии и частично даже биологии.
Но что, если мы встретимся с существами из вообще другой Вселенной с отличными от наших законами физики? Какие точки соприкосновения с ними мы сможем найти? Очевидно, что единственной общей вещью между нами и иновселянами будет математика. Ведь даже несмотря на отличные от наших законов физики, законы математики в их Вселенной будут такими же как и у нас. Невозможно существование какой-то иной математики. Математика никак не зависит от времени, пространства и любых других свойств той Вселенной, в которой мы существуем. Ведь если подумать, то даже до Большого Взрыва утверждение «дважды два равно четыре» должно было быть верным.
Рассуждая схожим образом, древнегреческий философ Платон пришел к выводу, что математика обладает независимым бытием и существует в неком нематериальном «мире форм». В доказательство своему утверждению Платон приводил правильные многогранники, позже в его честь названные платоновыми телами.

Рождение Вселенной
Мы подошли к самой красивой части «буддийского физмата»: гипотезе рождения Вселенной. Эта часть содержит достаточно много непростой метафизики, но начинается она с единственного постулата: все вещи существуют симметрично относительно друг друга. Я употребляю слово «существует», а не «возникает», потому что возникновение предполагает некий процесс во времени, а в мире абсолютных форм нет времени, оно появляется позже.
Одной из таких структур становятся иррациональные и трансцендентные числа, то есть числа не представимые в виде целочисленной дроби или корня уравнения. Количество цифр после запятой у таких чисел бесконечно. Самым известным трансцендентным числом является число π:
3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989.
Нетривиальные нули дзета-функции Римана (их мнимые части) соответствуют собственным значениям некоторого эрмитового оператора (неограниченного самосопряжённого оператора в гильбертовом пространстве).
Оказалось, что квантовый хаос прекрасно описывается распределением нетривиальных нолей функции Римана:

Британский научно-популярный писатель Джон Дербишир задавался вопросом на этот счёт:
Нетривиальные нули дзета-функции Римана появились при исследовании распределения простых чисел. Собственные значения случайных эрмитовых матриц появились при исследовании поведения систем субатомных частиц, подчиняющихся законам квантовой механики. Скажите, пожалуйста, что вообще может быть общего между простыми числами и поведением субатомных частиц?
Если бы он был знаком с «буддийским физматом», он бы знал ответ! Более того, «буддийский физмат» проливает свет и на то, почему наш мир на микроуровне, изучаемом квантовой механикой, кажется случайным, а на макроуровне абсолютно стабилен. Каждое следующее простое число случайно и невычислимо по точной формуле, но их распределение строго подчинено дзета-функции Римана. А каждая следующая цифра после запятой в иррациональном числе тоже абсолютно случайна: , но их общее количество на большом масштабе абсолютно стабильно: например, в первом миллионе цифр после запятой числа Пи 99959 нулей, 99758 единиц, 100026 двоек, 100229 троек, 100230 четвёрок, 100359 пятёрок, 99548 шестёрок, 99800 семёрок, 99985 восьмёрок и 100106 девяток. Получается, простые и иррациональные числа, прямо как наша Вселенная, строго детерминированы математикой, но кажутся случайными на микромасштабах.
Вывод
Гипотеза Римана
оглавление
вступление
простые числа
Теорема о простых числах
Например, только 4 простых числа, а именно 2, 3, 5 и 7, меньше числа 10. В случае 50 уже есть 15 меньших простых чисел, а именно
Приближение, данное в теореме о простых числах, дает неплохие значения. Например, под числом 73893 ровно 7293 простых числа, и оно содержит
Идеи Римана
Оригинальная работа 1859 г.
Дзета-функция Римана
Дзета-функция Римана
формулировка
Центральным открытием знаменитой работы Римана 1859 года было открытие, что все возможные нетривиальные нули находятся в так называемой критической полосе.
должен быть расположен.
Риман выдвинул свою гипотезу, исследуя произведение дзета-функции на гамма-функцию.
Прямая линия на плоскости комплексных чисел с действительной частью 1/2, следовательно, также инвариантна в этом отражении. Сам Риман пишет о нулях:
«[. ] и весьма вероятно, что все корни настоящие. Конечно, было бы желательно строгое доказательство этого; Тем временем, после нескольких мимолетных безуспешных попыток, я оставил его поиски в стороне, так как он казался ненужным для следующей цели моего расследования ».
Теоретико-вероятностный взгляд
Сравнение проводится с учетом справедливого подбрасывания монеты. Честная монета с возможными результатами «орел» и «решка» подбрасывается несколько раз подряд. В идеальной ситуации результат каждого броска абсолютно случайен и, более того, результаты бросков не зависят друг от друга. Таким образом, если орел был брошен первым, это не должно иметь никакого отношения к тому, идет ли решка или орел.
Если, с другой стороны, гипотеза Римана неверна, возникнет дисбаланс в распределении простых чисел в том смысле, что, например, будет неестественно большое количество чисел с четным числом простых множителей, таких как 10, 14, 25, 132, как числа с нечетным числом простых множителей, например 7, 8, 12, 18 и 125.
имея в виду
Нетривиальные нули и простые числа
Несмотря на сложную оценку, Риман пришел к результату.
была создана глубокая связь между простыми числами и нулями дзета-функции.
Выводы
Из гипотезы Римана, например, следует оценка остатка члена в теореме о простых числах ( Helge von Koch 1901):
Результат Коха эквивалентен гипотезе Римана. Его также можно записать как
история
Два французских математика Гурдон и Демишель начали новый эксперимент с методом Одлизко и Шёнхаге в 2004 году и проверили первые 10 триллионов нулей в октябре 2004 года, не найдя контрпримера. Хотя все расчеты являются численными методами, они показывают точно, а не только приблизительно, что исследуемые нули находятся на критической прямой.
Более поздние попытки доказательства или опровержения
Луи де Бранж де Бурсия занимался этой проблемой на протяжении десятилетий. В 1985 году (вскоре после доказательства гипотезы Бибербаха ) он представил доказательство, основанное на его теории гильбертовых пространств целых функций, в котором Питер Сарнак обнаружил ошибку. В 1989 году по случаю серии лекций в Институте Анри Пуанкаре он представил дополнительные доказательства, которые он сам вскоре признал ошибочными. В 2004 году он опубликовал новое свидетельство, которое было подвергнуто критическому анализу. Однако за много лет до этого Эберхард Фрейтаг привел контрпример к утверждению, сделанному в доказательствах, так что теперь доказательства считаются ложными.
Обобщенная гипотеза Римана.
Следующее утверждение обычно называют как обобщенный или общую гипотеза Римана :
Связанные гипотезы и эквивалентные формулировки
В аналитической теории чисел есть и другие гипотезы, связанные с гипотезой Римана. Мертенс гипотеза говорит
Как уже упоминалось, из гипотезы Римана в соответствии с Хельге фон Кохом есть границы для роста ошибочного члена теоремы о простых числах. Но результат фон Коха также эквивалентен гипотезе Римана. конец
следует гипотезе Римана.
где теорема о простых числах эквивалентна
ψ ( Икс ) знак равно Икс + О ( Икс ) <\ Displaystyle \ psi (х) = х + <\ mathcal
Гипотеза Линделёфа об организации дзета-функции вдоль критической линии слабее, чем гипотеза Римана, но все еще не доказана.
В 2002 году Джеффри Лагариас выдвинул гипотезу элементарной теории чисел, которая эквивалентна гипотезе Римана:
Свидетельские идеи из физики
Оператор по имени по Medal Поля победитель премии Конн в 1996 году «почти» припадки. Однако Конн еще не смог исключить существование дополнительных нулей вне критической прямой.
Связь гипотезы Римана с одномерными квазикристаллами была предложена Фрименом Дайсоном в 2009 году.
Нули дзета-функции Римана
Нули дзета-функции Римана
| Задачи тысячелетия |
|---|
| Равенство классов P и NP |
| Гипотеза Ходжа |
| Гипотеза Пуанкаре |
| Гипотеза Римана |
| Квантовая теория Янга — Миллса |
| Существование и гладкость решений уравнений Навье — Стокса |
| Гипотеза Берча и Свиннертона — Дайера |
Гипо́теза Ри́мана о распределении нулей дзета-функции Римана была сформулирована Бернхардом Риманом в 1859 году.
Функция ζ(s) определена для всех комплексных 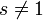
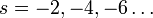
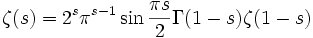
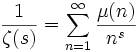
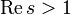
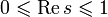
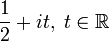
Все нетривиальные нули дзета-функции имеют действительную часть, равную
Обобщённая гипотеза Римана состоит из того же самого утверждения для обобщений дзета-функций, называемых L-функциями Дирихле.
На 2004 год проверены более 10 13 первых нулей. [1]
Большинство математиков верят, что гипотеза верна. Многие утверждения о распределении простых чисел, в том числе о сложности некоторых целочисленных алгоритмов, доказаны в предположении верности гипотезы Римана. В то время как не существует простой закономерности, описывающей распределение простых чисел среди натуральных, Риман обнаружил, что число π(x) простых чисел, не превосходящих x, выражается через распределение нетривиальных нулей дзета-функции.
Гипотеза Римана входит в список семи «проблем тысячелетия», за решение каждой из которых Математический институт Клэя (Clay Mathematics Institute, Кембридж, Массачусетс) выплатит приз в 1 млн. долларов США. Интересно, что опровержение гипотезы Римана не даст права на получение приза. [1]
Содержание
История
В 1896 Адамар и Валле-Пуссен независимо доказали, что нули дзета-функции не могут лежать на прямых 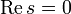
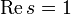
В 1900 Давид Гильберт включил гипотезу Римана в список 23 нерешённых проблем как часть восьмой проблемы, совместно с гипотезой Гольдбаха.
В 1914 Харди доказал, что на критической линии находится бесконечно много нулей, а позже Харди и Литлвуд дали оценку снизу доли нулей, лежащей на критической линии, которую потом улучшали разные математики.
Некоторые нетривиальные нули располагаются экстремально близко друг к другу. Это свойство известно как «явление Лемера (Lehmer)».
Титчмарш, Ворос в 1987 показали, что дзета-функция может быть разложена в произведение через свои нетривиальные нули в разложение Адамара.
Группа математиков Университета Пардье (Purdue University, USA) под руководством Луи де Бранжа (Louis De Branges de Bourcia) предложила доказательство гипотезы Римана [2], которое, однако, оказалось неверным [3].
Эквивалентные формулировки
В 1901 Хельге фон Кох показал, что гипотеза Римана эквивалентна следующему утверждению о распределении простых чисел:
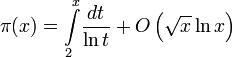
Интересные факты
Знаменит ответ Гильберта на вопрос о том, каковы будут его действия, если он по какой-либо причине проспит пятьсот лет и вдруг проснется. Математик ответил, что самым первым делом он спросит была ли доказана гипотеза Римана.
Примечания
Ссылки
См. также
Полезное
Смотреть что такое «Нули дзета-функции Римана» в других словарях:
Дзета-функция Римана — Запрос «Дзета функция» перенаправляется сюда; см. также другие значения. Качественный график дзета функции Римана на действительной оси. Слева от нуля значения функции увеличены в 100 раз … Википедия
ДЗЕТА-ФУНКЦИЯ — z ф у нкция, 1) Д. ф. в теории чисел класс аналитич. функций комплексного переменного, состоящий из z функции Римана, ее обобщений и аналогов. Д. ф. и их обобщения в виде L функций (см. Дирихле L функции )лежат в основе современной аналитич.… … Математическая энциклопедия
РИМАНА ГИПОТЕЗЫ — в а н а л и т и ч е с к о й т е о р и и ч и с е л пять гипотез, высказанных Б. Риманом (В. Riemann, 1876) относительно распределения нетривиальных нулей дзета функции и относительно выражения через эти нули числа простых чисел, не превосходящих… … Математическая энциклопедия
Дзета-функция — 1) аналитическая функция комплексного переменного s = σ + it, определяемая при σ > 1 формулой Эту функцию для действительных s ввёл в математический анализ Л. Эйлер (1737), а для комплексных s впервые изучал немецкий… … Большая советская энциклопедия
Гипотеза Римана — Задачи тысячелетия Равенство классов P и NP Гипотеза Ходжа Гипотеза Пуанкаре Гипотеза Римана Квантовая теория Янга Миллса Существование и гладкость решений уравнений Навье Стокса Гипотеза Бёрча Свиннертон Дайера Гипотеза Римана о… … Википедия
Нуль функции — Нули косинуса на интервале [ 2π,2π] (красные точки) Нуль функции в математике элемент из области определения функции, в котором она принимает нулевое значение. Например, для функции … Википедия
Сельберг, Атле — Атле Сельберг норв. Atle Selberg … Википедия