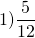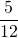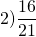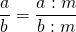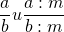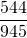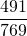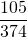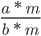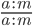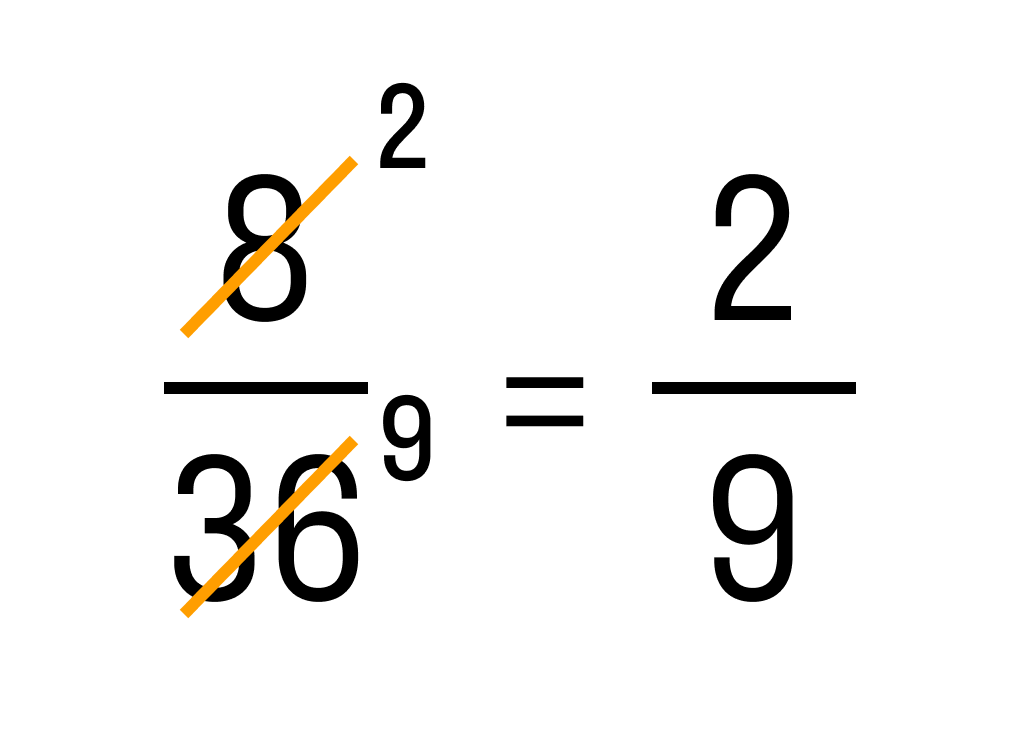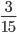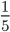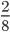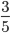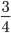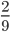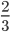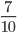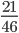что такое несократимая дробь
Несократимая дробь
Несократимая дробь — это дробь, числитель и знаменатель которой являются взаимно-простыми числами.
То есть единственным общим делителем числителя и знаменателя несократимой дроби является единица.
Делители числителя: 1; 5
Делители знаменателя: 1 ; 2; 3; 4; 6; 12.
НОД (5; 12) =1, следовательно, 5 и 12 — взаимно-простые числа. Поэтому дробь
Делители числителя: 1 ; 2; 4; 8; 16.
Делители знаменателя: 1 ; 3; 7; 21.
Наибольший (и единственный) общий делитель числителя и знаменателя — единица. Значит, числитель и знаменатель — взаимно-простые числа. Поэтому данная дробь — несократимая.
Согласно основному свойству дроби, дробь не изменится, если её числитель и знаменатель разделить на одно и то же число, отличное от нуля:
— две различные записи одного и того же числа.
В математике принято ответ записывать в виде несократимой дроби. То есть если числитель и знаменатель дроби можно разделить на одно и то же число, необходимо это сделать, иначе ответ не считается правильным.
Вот почему столь важно уметь определять, является ли дробь несократимой.
Как определить, является ли дробь несократимой?
1) Можно разложить числитель и знаменатель на простые множители и найти наибольший общий делитель. Если он равен 1, дробь несократима.
— несократимая дробь, поскольку наибольший общий делитель числителя и знаменателя равен единице и 544 и 945 — взаимно-простые числа.
2) Если числитель и знаменатель — простые числа, то они являются взаимно-простыми, а дробь, соответственно, — несократимой.
несократима, так как 491 и 769 — простые числа (проверили по таблице простых чисел).
3) Можно проверять делимость числителя и знаменателя, используя признаки делимости.
Если ни один из делителей одного числа не является делителем другого, то общий делитель числителя и знаменателя — единица, то есть они являются взаимно-простыми числами, а дробь — несократимой.
Числитель 105 делится на 5, 105:5=21. 21 делится на 3 и на 7. Следовательно, делители 105: 1; 3; 5; 7; 105.
Искать все делители знаменателя 374 не обязательно. Достаточно проверить, а не делится ли он на один из делителей числителя:
на 5 не делится (запись заканчивается не на 0 и не на 5),
на 7 не делится (можно проверить непосредственным делением),
Значит 1 — единственный общий делитель 105 и 374, они являются взаимно-простыми числами, а дробь — несократимой.
Сократимые дроби
Вы будете перенаправлены на Автор24
Сократимые и несократимые дроби
Все обыкновенные дроби делятся на сократимые и несократимые дроби. Такое разделение дробей зависит от наличия или отсутствия общих делителей числителя и знаменателя, отличных от единицы.
Правила проверки дроби на сократимость
В самых простых случаях проверить дробь на сократимость можно с помощью признаков делимости.
Готовые работы на аналогичную тему
Правило проверки обыкновенной дроби на сократимость
Вычислить наибольший общий делитель (НОД) числителя и знаменателя данной дроби:
Решение.
НОД вычислим по алгоритму Евклида:
Сокращение дробей
Чтобы сократить дробь, нужно ее числитель и знаменатель разделить на их общий положительный отличный от единицы делитель. В результате сокращения дроби получают новую дробь, равную исходной, но с меньшим числителем и знаменателем.
Приведение обыкновенных дробей к несократимому виду
Таким образом, для приведения обыкновенной дроби к несократимому виду необходимо ее числитель и знаменатель разделить на их НОД.
Под фразой «сократите дробь» чаще всего подразумевают приведение исходной дроби к несократимому виду. Т.е. именно деление числителя и знаменателя на их НОД, а не деление на любой их общий делитель.
Правило сокращения дробей
Найти НОД числителя и знаменателя дроби.
Разделить числитель и знаменатель дроби на их НОД, в результате чего получают несократимую дробь, равную исходной.
Решение.
Воспользуемся правилом сокращения дробей:
Наиболее удобным является алгоритм Евклида:
\[231=187\cdot 1+44\]\[187=44\cdot 4+11\]\[44=11\cdot 4\]
Таким образом, НОД($187, 231)=11$.
Иногда для сокращения дробей (в более простых случаях) применяют способ \textit<разложения дроби на простые множители>, после чего убираются все общие множители из числителя и знаменателя. Этот способ вытекает из правила сокращения дробей, т.к. НОД равен произведению всех общих простых множителей числителя и знаменателя.
Решение.
Разложим числитель и знаменатель на простые множители:
Избавимся от общих множителей в числителе и знаменателе (для удобства их часто зачеркивают):
Решение.
Что такое несократимые дроби
Данная статья посвящена рассмотрению сократимых и несократимых дробей. Приведем примеры, дадим определения сократимых и несократимых дробей. Выясним, как определить, можно ли сократить конкретную дробь.
Сократимые и несократимые дроби
Все обыкновенные дроби вида a b можно разделить на сократимые и несократимые. Разделение объясняется соответственно наличием или отсутствием общих для числителя и знаменателя дроби делителей. Приведем определения.
Определение. Сократимая дробь
Обыкновенная сократимая дробь – такая дробь, для числителя и знаменателя которой существует положительный общий делитель, отличный от единицы.
Обыкновенная несократимая дробь – такая дробь, числитель и знаменатель которой являются взаимно простыми числами, то есть имеют единственный общий положительный делитель, равный единице.
Приведем примеры сократимых и несократимых дробей.
Примеры сократимых дробей
Дробь 15 45 – сократимая. Действительно, как числитель, так и знаменатель можно разделить на 5. Другими словами, числитель и знаменатель этой дроби имеют общий делитель.
Дробь 7 12 – несократимая, так как ее числитель и знаменатель являются взаимно простыми числами.
Проверка дроби на сократимость
Часто с первого взгляда на конкретную дробь сложно сказать, является она сократимой или несократимой. Конечно, исключения составляют простые случаи, когда по признакам делимости сразу можно выявить общий делитель числителя и знаменателя.
Правило проверки дроби на сократимость
Вычисляем наибольший общий делитель числителя и знаменателя дроби.
Посмотрим на практическое применение этого правила.
Пример. Сократима ли дробь?
539 = 495 · 1 + 44 495 = 44 · 11 + 11 44 = 11 · 4
В математических выкладках, если при вычислениях получилась сократимая дробь, принято производить ее сокращение и записывать в виде несократимой дроби.
Что ты хочешь узнать?
Ответ
В математике, несократимая дробь (также приведённая дробь) — дробь, которую невозможно сократить.
Ответ
В математике, несократимая дробь — дробь, которую невозможно сократить. Иначе говоря, значение несократимой дроби не допускает более простое представление в виде дроби.
Несократимая дробь — это дробь, числитель и знаменатель которой являются взаимно-простыми числами.
НЕСОКРАТИМАЯ ДРОБЬ — дробь, числитель и знаменатель которой не имеют общих делителей
Дроби делятся на сократимые и несократимые дроби. Рассмотрим подробнее какую дробь называются сократимой и какую дробь называют несократимой.
Сократимая дробь, определение и примеры.
Определение:
Сократимая дробь – это дробь у которой числитель и знаменатель имеют общий положительный делитель не равный нулю и единице.
Например:
Докажите, что дробь (frac ) является сократимой.
Решение:
Распишем числитель и знаменатель на простые множители, найдем их наибольший общий делитель (НОД).
20=2⋅2⋅5
35=5⋅7
Так как у числителя и знаменателя повторяется множитель 5, это число и будет их наибольшим общим делителем.
НОД(20, 35)=5
Сократим дробь на НОД.
Из сократимой дроби (frac ) получили несократимую дробь (frac ).
Несократимая дробь, определение и примеры.
Какие же дроби несократимые или что значит несократимая дробь? Ответ на вопрос кроется в определении.
Определение:
Несократимая дробь – это дробь у которой числитель и знаменатель имеют только один общий делитель равный единице, то есть числитель и знаменатель являются взаимно-простыми числами.
Рассмотрим пример:
Докажите, что дробь (frac ) является несократимой дробью.
Решение:
Число 137 является простым, так как оно делиться на 1 и на само себя.
Число 149 является простым, так как оно делиться на 1 и на само себя.
У числителя 137 и знаменателя 149 нет общих делителей, поэтому дробь (frac ) является несократимой.
Правило несократимой дроби.
Пример:
Запишите сократимую дробь в виде несократимой обыкновенной дроби (frac ).
Решение:
По правилу несократимой дроби распишем числитель и знаменатель на простые множители.
55=5⋅11
100=5⋅2⋅2⋅5
Видим, что у числителя и знаменателя есть общий множитель равный 5, поэтому сокращаем дробь на 5.
Ответ: получили несократимую дробь (frac ).
Неправильные сократимые и несократимые дроби.
Чтобы перевести неправильную сократимую дробь в неправильную несократимую дробь, мы пользуемся теми же правилами, что и для правильной сократимой дроби. Рассмотрим пример:
Запишите неправильную сократимую дробь в виде неправильной несократимой дроби (frac ).
Решение:
Разложим числитель и знаменатель на простые множители.
32=2⋅2⋅2⋅2⋅2
20=5⋅2
Общий множитель у числителя и знаменателя равен 2. Распишем
Ответ: получили несократимую неправильную дробь (frac ).
Вопросы по теме:
Как узнать сократима ли дробь?
Ответ: чтобы узнать сократима ли дробь для начала нужно расписать числитель и знаменатель на простые множители, а потом посмотреть если у них общие множители, если есть, то дробь сократима, иначе – несократима. Рассмотрим пример.
Определите сократима ли дробь (frac ).
Решение:
Распишем числитель и знаменатель на простые множители.
16=2⋅2⋅2⋅2
25=5⋅5
Видно, что у числителя и знаменателя нет общих множителей (одинаковых множителей), следовательно, дробь несократима.
Пример:
Сколько несократимых правильных дробей: а) (frac ) б) (frac ) в) (frac ) г) (frac ).
Решение:
а) У числителя и знаменателя дроби (frac ) (8=2⋅2⋅2, 25=5⋅5) нет общих множителей, поэтому это правильная несократимая дробь. По условию это дробь нам подходит.
б) У числителя и знаменателя дроби (frac ) (6=2⋅3, 4=2⋅2, (frac =frac =frac ) ) есть общий множитель равный 2, поэтому это дробь сократимая и еще неправильная, потому что числитель больше знаменателя. По условию задания эта дробь нам не подходит.
в) Числитель и знаменатель дроби (frac ), 5 и 13 простые числа, поэтому общих множителей кроме 1 у них нет, дробь несократимая. Так как числитель больше знаменателя дробь неправильная, поэтому по условию задания нам она не подходит.
г) Числитель и знаменатель дроби (frac ) (36=2⋅2⋅3⋅3, 44=2⋅2⋅11) имеют общий множитель равный 4, поэтому дробь (frac =frac =frac ) является сократимой, правильной. Нам по условию задания не подходит.
Ответ: (frac ) несократимая, правильная дробь.
Пример:
Сколько имеется правильных несократимых дробей со знаменателем: а) 145 б) 123 в) 133 г) 115.
Решение:
а) Распишем на простые множители знаменатель 145:
145=5⋅29
Нужно исключить все числа от 1 до 144 кратные 5 и 29.
На 5 делится: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110, 115, 120, 125, 130, 135, 140.
На 29 делится: 29, 58, 87, 116.
В сумме получаем 32 числа, которые имеют общий множитель с число 145. Всего у нас чисел 144.
144-32=112
Ответ: 112 правильных несократимых дробей со знаменателем 145.
б) Распишем на простые множители знаменатель 123:
123=3⋅41
В диапазоне чисел от 1 до 122 исключаем числа кратные 3 и 41.
На число 3 делится, поэтому не могут находиться в числителе: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99, 102, 105, 108, 111, 114, 117, 120.
На 41 делится: 41, 82.
В сумме получаем 40+2=42 числа, которые имеют общий множитель с число 123, поэтому мы их исключим. Всего у нас чисел 122.
122-42=80
Ответ: 80 правильных несократимых дробей со знаменателем 123.
в) Распишем на простые множители знаменатель 133:
133=7⋅19
Числа от 1 до 132 исключаем, они делятся на 7 и 19, для того чтобы получить все несократимые дроби от (frac ) до (frac ).
Число 7 кратно: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126. Всего 18 чисел.
Число 19 кратно:19, 38, 57, 76, 95, 114. Всего 6 чисел.
132-18-6=108
Ответ: 108 правильных несократимых дробей со знаменателем 133.
г) Распишем на простые множители знаменатель 115:
115=5⋅23
Числа от 1 до 114 исключаем.
На 5 делится: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110. Всего 22 числа.
На 23 делится число: 23, 46, 96, 92. Всего 4 чисел.
114-22-4=88
Ответ: 88 правильных несократимых дробей со знаменателем 115.
Нестандартная задача по математике:
Когда нельзя сокращать сократимую обыкновенную дробь?
Ответ: когда сократимая обыкновенная дробь является номером углового дома или квартала.
Сократимые и несократимые дроби.
Дроби делятся на сократимые и несократимые дроби. Рассмотрим подробнее какую дробь называются сократимой и какую дробь называют несократимой.
Сократимая дробь, определение и примеры.
Определение:
Сократимая дробь – это дробь у которой числитель и знаменатель имеют общий положительный делитель не равный нулю и единице.
Например:
Докажите, что дробь \(\frac<20><35>\) является сократимой.
Решение:
Распишем числитель и знаменатель на простые множители, найдем их наибольший общий делитель (НОД).
20=2⋅2⋅5
35=5⋅7
Так как у числителя и знаменателя повторяется множитель 5, это число и будет их наибольшим общим делителем.
НОД(20, 35)=5
Сократим дробь на НОД.
Из сократимой дроби \(\frac<20><35>\) получили несократимую дробь \(\frac<4><7>\).
Несократимая дробь, определение и примеры.
Какие же дроби несократимые или что значит несократимая дробь? Ответ на вопрос кроется в определении.
Определение:
Несократимая дробь – это дробь у которой числитель и знаменатель имеют только один общий делитель равный единице, то есть числитель и знаменатель являются взаимно-простыми числами.
Рассмотрим пример:
Докажите, что дробь \(\frac<137><149>\) является несократимой дробью.
Решение:
Число 137 является простым, так как оно делиться на 1 и на само себя.
Число 149 является простым, так как оно делиться на 1 и на само себя.
У числителя 137 и знаменателя 149 нет общих делителей, поэтому дробь \(\frac<137><149>\) является несократимой.
Правило несократимой дроби.
Пример:
Запишите сократимую дробь в виде несократимой обыкновенной дроби \(\frac<55><100>\).
Решение:
По правилу несократимой дроби распишем числитель и знаменатель на простые множители.
55=5⋅11
100=5⋅2⋅2⋅5
Видим, что у числителя и знаменателя есть общий множитель равный 5, поэтому сокращаем дробь на 5.
Ответ: получили несократимую дробь \(\frac<11><20>\).
Неправильные сократимые и несократимые дроби.
Чтобы перевести неправильную сократимую дробь в неправильную несократимую дробь, мы пользуемся теми же правилами, что и для правильной сократимой дроби. Рассмотрим пример:
Запишите неправильную сократимую дробь в виде неправильной несократимой дроби \(\frac<32><20>\).
Решение:
Разложим числитель и знаменатель на простые множители.
32=2⋅2⋅2⋅2⋅2
20=5⋅2
Общий множитель у числителя и знаменателя равен 2. Распишем
Ответ: получили несократимую неправильную дробь \(\frac<16><5>\).
Вопросы по теме:
Как узнать сократима ли дробь?
Ответ: чтобы узнать сократима ли дробь для начала нужно расписать числитель и знаменатель на простые множители, а потом посмотреть если у них общие множители, если есть, то дробь сократима, иначе – несократима. Рассмотрим пример.
Определите сократима ли дробь \(\frac<16><25>\).
Решение:
Распишем числитель и знаменатель на простые множители.
16=2⋅2⋅2⋅2
25=5⋅5
Видно, что у числителя и знаменателя нет общих множителей (одинаковых множителей), следовательно, дробь несократима.
Пример:
Сколько несократимых правильных дробей: а) \(\frac<8><25>\) б) \(\frac<6><4>\) в) \(\frac<13><5>\) г) \(\frac<36><44>\).
Решение:
а) У числителя и знаменателя дроби \(\frac<8><25>\) (8=2⋅2⋅2, 25=5⋅5) нет общих множителей, поэтому это правильная несократимая дробь. По условию это дробь нам подходит.
б) У числителя и знаменателя дроби \(\frac<6><4>\) (6=2⋅3, 4=2⋅2, \(\frac<6><4>=\frac<2 \times 3><2 \times 2>=\frac<3><2>\) ) есть общий множитель равный 2, поэтому это дробь сократимая и еще неправильная, потому что числитель больше знаменателя. По условию задания эта дробь нам не подходит.
в) Числитель и знаменатель дроби \(\frac<13><5>\), 5 и 13 простые числа, поэтому общих множителей кроме 1 у них нет, дробь несократимая. Так как числитель больше знаменателя дробь неправильная, поэтому по условию задания нам она не подходит.
г) Числитель и знаменатель дроби \(\frac<36><44>\) (36=2⋅2⋅3⋅3, 44=2⋅2⋅11) имеют общий множитель равный 4, поэтому дробь \(\frac<36><44>=\frac<4 \times 9><4 \times 11>=\frac<9><11>\) является сократимой, правильной. Нам по условию задания не подходит.
Ответ: \(\frac<8><25>\) несократимая, правильная дробь.
Пример:
Сколько имеется правильных несократимых дробей со знаменателем: а) 145 б) 123 в) 133 г) 115.
Решение:
а) Распишем на простые множители знаменатель 145:
145=5⋅29
Нужно исключить все числа от 1 до 144 кратные 5 и 29.
На 5 делится: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110, 115, 120, 125, 130, 135, 140.
На 29 делится: 29, 58, 87, 116.
В сумме получаем 32 числа, которые имеют общий множитель с число 145. Всего у нас чисел 144.
144-32=112
Ответ: 112 правильных несократимых дробей со знаменателем 145.
б) Распишем на простые множители знаменатель 123:
123=3⋅41
В диапазоне чисел от 1 до 122 исключаем числа кратные 3 и 41.
На число 3 делится, поэтому не могут находиться в числителе: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99, 102, 105, 108, 111, 114, 117, 120.
На 41 делится: 41, 82.
В сумме получаем 40+2=42 числа, которые имеют общий множитель с число 123, поэтому мы их исключим. Всего у нас чисел 122.
122-42=80
Ответ: 80 правильных несократимых дробей со знаменателем 123.
в) Распишем на простые множители знаменатель 133:
133=7⋅19
Числа от 1 до 132 исключаем, они делятся на 7 и 19, для того чтобы получить все несократимые дроби от \(\frac<1><133>\) до \(\frac<132><133>\).
Число 7 кратно: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126. Всего 18 чисел.
Число 19 кратно:19, 38, 57, 76, 95, 114. Всего 6 чисел.
132-18-6=108
Ответ: 108 правильных несократимых дробей со знаменателем 133.
г) Распишем на простые множители знаменатель 115:
115=5⋅23
Числа от 1 до 114 исключаем.
На 5 делится: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110. Всего 22 числа.
На 23 делится число: 23, 46, 96, 92. Всего 4 чисел.
114-22-4=88
Ответ: 88 правильных несократимых дробей со знаменателем 115.
Нестандартная задача по математике:
Когда нельзя сокращать сократимую обыкновенную дробь?
Ответ: когда сократимая обыкновенная дробь является номером углового дома или квартала.
Сокращение обыкновенных дробей
Что такое «сокращение дробей»
Математика любит точность и краткость: лохматыми громоздкими числами ее расположение не заслужить. Поэтому, следуя негласному правилу, сокращайте все, что можно сократить.
Сократить дробь — значит разделить ее числитель и знаменатель на их общий делитель. Общий делитель должен быть положительным и не равен нулю и единице.
В результате сокращения вы получаете новую дробь, равную исходной дроби. Такие дроби равны по основному свойству:
Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число — получится дробь, равная данной.
С основным свойством дроби знакомятся в 5 классе, но встречаться оно будет до самого окончания школы. Поэтому запоминаем, как выглядит основное свойство дроби в виде буквенных выражений:


где a, b, m — натуральные числа.
Графически сокращение дробей обычно записывается вот так:
Числитель и знаменатель зачеркиваются черточками. В этом примере числитель — 8, знаменатель — 36. Справа над ними записывают результаты деления числителя и знаменателя на их общий делитель. Общий делить 8 и 36 — 4. Это число не нужно записывать.
Пример 1. Сократим обыкновенную дробь
Разделим числитель и знаменатель на общий делитель 3.

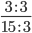
Сокращение выполнено: 
Пример 2. Сократим обыкновенную дробь
Разделим числитель и знаменатель на общий делитель 2.

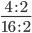
Сокращение выполнено: 
Приведение дробей к несократимому виду
Смысл сокращения дробей в том, чтобы в результате сокращения в числителе и знаменателе оказались наименьшие из возможных чисел.
Так, в результате сокращения в примере 2, мы из дроби 
Выходит, что дробь выдержит еще одно сокращение и придет к виду
Сокращая дробь, стремитесь в итоге получить несократимую дробь.
Разделите числитель и знаменатель дроби на их НОД (наибольший общий делитель). Так вы приведете дробь к несократимому виду.
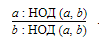
a : НОД(a, b) и b : НОД(a, b) — взаимно простые числа.
Два целых числа a и b называются взаимно простыми, если их наибольший общий делитель равен единице, НОД(a, b) = 1.
Пример 3. Приведите обыкновенную дробь к несократимому виду
Найдем НОД числителя и знаменателя. НОД = 12
Найдем частное: 12 : 12 = 1

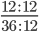
Сокращение выполнено: 
Пример 4. Приведите обыкновенную дробь к несократимому виду
Найдем НОД числителя и знаменателя. НОД = 5
Найдем частное: 15 : 5 = 3

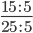
Сокращение выполнено: 
Правило сокращения дробей
Чтобы без труда сокращать любую обыкновенную дробь, запомните правило.
Выполняйте сокращение дробей по следующему алгоритму:
В 6 классе каждая вторая задачка — с дробями. Чтобы легко управляться с ними и уметь сокращать любые числа, нужно хорошо потренироваться. Давайте разберем еще несколько примеров сокращения обыкновенных дробей.
Чтобы легко сокращать дроби, нужно уметь быстро находить НОД числителя и знаменателя. Для этого неплохо бы знать таблицу умножения и уметь раскладывать числа на простые множители.
Чтобы найти НОД числителя и знаменателя, разложим числа на простые множители.
36 = 2 * 2 * 3 * 3
84 = 2 * 2 * 3 * 7
Перемножаем все общие множители между собой 2 * 2 * 3 = 12.
НОД 36 и 84 = 12.
Пример 5. Сократите дробь
Разложим числа в числителе и знаменателе на множители.
135 = 9 * 3 * 5
180 = 9 * 2 * 2 * 5
Мысленно убираем все общие множители и перемножаем оставшиеся.

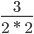
Сокращение выполнено: 
Пример 6. Сократите обыкновенную дробь
Найдем НОД числителя и знаменателя. НОД = 9

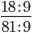
Сокращение выполнено: 
Дробь можно сократить, последовательно сокращая числитель и знаменатель на общий делитель. Такой способ подходит, если в числителе и знаменателе стоят крупные числа, и вы не уверены в подобранном НОД.
Пример 6. Сократите дробь:

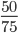
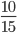
Сокращение выполнено: 
Пример 7. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
168 = 2 * 2 * 2 * 3 * 7
240 = 2 * 2 * 2 * 2 * 3 * 5
Перемножаем все общие множители между собой 2 * 2 * 2 * 3 = 24
НОД 168 и 240 равен 24
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 168 : 24 = 7

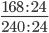
Сокращение выполнено: 
Пример 8. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
360 = 2 * 2 * 2 * 3 * 3 * 5
540 = 2 * 2 * 3 * 3 * 3 * 5
Перемножаем все общие множители между собой 2 * 2 * 3 * 3 * 5 = 180
НОД 360 и 540 равен 180
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 360 : 180 = 2

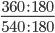
Сокращение выполнено: 
Пример 8. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
420 = 2 * 2 * 3 * 5 * 7
2520 = 2 * 2 * 2 * 3 * 3 * 5 * 7
Перемножаем все общие множители между собой 2 * 2 * 3 * 5 * 7 = 420
НОД 420 и 2520 равен 420
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 420 : 420 = 1

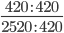
Сокращение выполнено. Дробь приведена к несократимому виду: 
Пример 9. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
1575 = 3 * 3 * 5 * 5 * 7
3450 = 2 * 3 * 5 * 5 * 23
Перемножаем все общие множители между собой 3 * 5 * 5 = 75
НОД 1575 и 3450 равен 72
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 1575 : 75 = 21

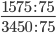
Сокращение выполнено. Дробь приведена к несократимому виду: 
Иногда разложение на простые множители занимает немало времени, особенно если раскладываемые числа большие, как в двух предыдущих примерах. Чтобы быстро разложить любое число на простые множители, можно обратиться к онлайн-калькулятору — в интернете их много. Воспользуйтесь одним из них.
Если времени совсем не хватает — можно использовать онлайн-калькулятор и для нахождения НОД. Однако не стоит постоянно прибегать к калькулятору для решения задач, пока вы не научитесь уверенно и быстро вычислять сами.